R1 и R2 - R-компоненты цвета пикселя наложенных изображений;
A - вещественное число из диапазона [0.0, 1.0].
В 3ds Max прозрачность регулируется свойством Opacity (рис. 4), которое имеют материалы.

В пособии рассматриваются методы и алгоритмы векторных графических систем, основанных на полигональных моделях и сплайнах. К таким системам относятся, например, 3ds Max или Maya фирмы Autodesk.
Зd-полигональный объект - это множество полигонов, для воспроизведения которых достаточно знать координаты вершин каждого полигона.
Так, сферу (рис. 1) можно представить в виде множества трапеций.

Рис. 1. Полигональная модель сферы
Сплайн (рис. 2) строится либо по контрольным вершинам, либо по вершинам, лежащим непосредственно на сплайне.
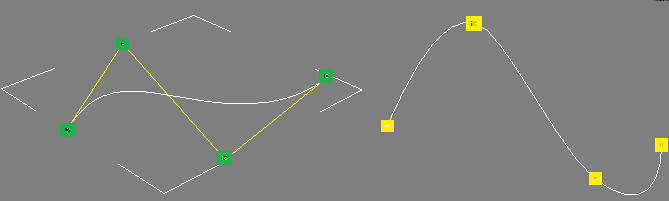
Рис. 2. Сплайны
Несложно придумать способ хранения данных о координатах вершин полигонов и сплайнов.
Растровые данные в таких системах употребляется для оформления объектов, например, для создания текстуры.
На рис. 3 показана сфера с наложенной текстурой, созданной по растровому образу, приведенному в верхней части рисунка.
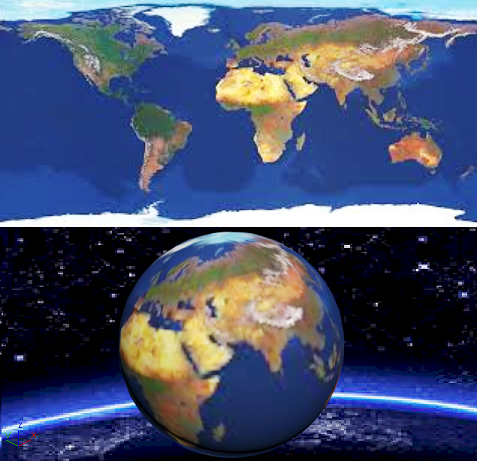
Рис. 3. Текстура, созданная по растровому образу, употреблена при выводе сферы
Фон, на котором изображена сфера, так же создан по растровым данным.
Файлы с растровыми данными хранят сведения цвете пикселей, составляющих изображение. Нередко для задания цвета употребляется RGB-система цветов, основанная на том факте, что любой оттенок можно получить, смешивая в соответствующих пропорциях красный (red), зеленый (green) и синий (blue) цвета.
Если для хранения составляющей цвета выделить 8 бит памяти, то для задания значения составляющей можно взять любое число от 0 до 255. Таким образом, всего можно получить 2563 = 16777216 цветовых оттенков.
Прозрачность реализуется в результате введения в систему цветов альфа-составляющей (система RGBA). В случае наложения 2-х изображений результирующий цвет каждого пикселя можно определить следующим образом (на примере R-компоненты):
R = R1 * (1.0 - A) + R2 * A,
где
R1 и R2 - R-компоненты цвета пикселя наложенных изображений;
A - вещественное число из диапазона [0.0, 1.0].
В 3ds Max прозрачность регулируется свойством Opacity (рис. 4), которое имеют материалы.

Рис. 4. Вывод объектов с Opacity материала сферы, равным соответственно 70, 30 и 10
Рисунок можно с Opacity = 70 можно получить, запустив следующий MaxScript-код:
delete $*
-- Создаем звезду как сплайн
str = star radius1:55 radius2:20 numPoints:5 rotation:(angleAxis -18 [0, 0, 1])
-- Конвертируем сплайн в полигональный объект
convertTo str PolyMeshObject
-- Материал для звезды
std = standard diffuse:red selfIllumColor:(color 255 0 0) showInViewport:true
std.useSelfIllumColor = on
meditMaterials[1] = std
str.material = std
-- Редактируем вершины звезды
str.verts[1].pos = [22, -6, 0]
str.verts[2].pos = [52, 16, 0]
str.verts[3].pos = [14, 19, 0]
str.verts[4].pos = [0, 55, 0]
str.verts[5].pos = [-14, 19, 0]
str.verts[6].pos = [-52, 16, 0]
str.verts[7].pos = [-22, -6, 0]
str.verts[8].pos = [-32, -44, 0]
str.verts[9].pos = [0, -23, 0]
str.verts[10].pos = [32, -44, 0]
-- Материал для сферы
std2 = standard diffuse:[200, 200, 200] opacity:70
meditMaterials[2] = std2
-- Создаем сферу
sp = sphere radius:60 segs:32
sp.material = std2
В качестве примера растровых графических систем можно указать, например, Microsoft Paint или Adobe Photoshop, работающий преимущественно с растровыми изображениями.
2d-чертеж, например, детали или сборочной единицы создается из следующих примитивов:
Некоторые примитивы можно наблюдать на приводимом ниже чертеже детали (рис. 1.1).
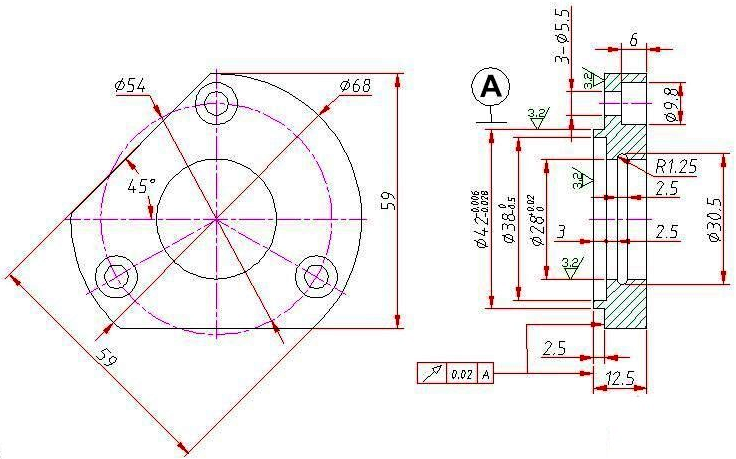
Рис. 1.1. Чертеж 2d
Примитивы обладают свойствами. Так, 2d-линии и фигуры имеют следующие свойства:
В Автокаде группа примитивов может быть объединена в составной примитив - блок, имеющий следующий свойства:
Блоком, пока он не разрушен, манипулируют как единым целым.
На рис. 1.2 показана модель резистора, выполненная в Автокаде как блок.

Рис. 1.2. Модель резистора до и после вставки
Модель включает еще два блока, употребляемых для представления выводов. Блок-вывод имеет атрибут "Номер вывода". Блок-резистор имеет атрибут "Позиционное обозначение".
Компоненты блока размещены на разных слоях рисунка:
| Компонент | Слой | Образующие примитивы |
|---|---|---|
| Условное графическое обозначение элемента | GATE | DRAW-примитивы Автокада |
| Вывод | PINCON | Вставленный блок $pin |
| Номер вывода | PINNUM | Атрибут модели элемента |
| Позиционное обозначение элемента | REFDES | Атрибут модели элемента |
Пример взят из работы AutoLISP в задаче создания графической модели элемента электрической схемы.
В 3ds Max объекты можно объединить в группу, например:
delete $*
cl = cylinder radius:6 height:20
sp = sphere radius:8 pos:[0, 0, 28]
gr = group #(cl, sp)
move gr [15, - 15, 0]
sp.radius = 16
sp.pos = [15, - 15, 36]
При этом свойства объектов доступны для изменения, что демострируют две последние строчки вышеприведенного кода.
Так же объекты можно связать, установив между ними отношение родитель - ребенок, например:
delete $*
cl = cylinder radius:6 height:20
sp = sphere radius:8 pos:[0, 0, 28]
sp.parent = cl -- Подчиняем сферу цилиндру
move cl [15, - 15, 0]
Перемещение цилиндра повлечет перемещение связанной с ним сферы.
Различные проекции чертежа (фронтальная, вид сверху и др.) можно создать по известному 3d-изображению.
Можно решить и обратную задачу - воспроизвести 3d-рисунок по его известным 2d-проекциям.
Есть системы, например, 3ds Max, не оперирующие 2d-примитивами, но использующие для построения 2d-фигур 3d-кривые (сплайны).
Так, окружность (рис. 1.3) после перевода сплайн модифицируется в 3d-кривую в результате перемещения одной или нескольких вершин.
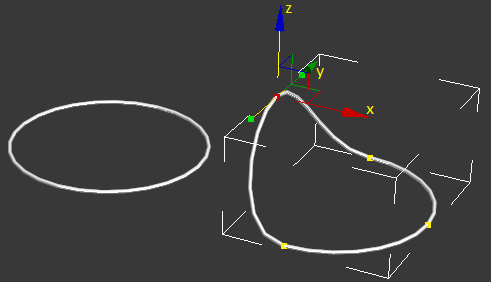
Рис. 1.3. Окружность и 3d-кривая, созданная в результате модификации окружности
Тот же результат можно получить, применив модификатор Edit_Spline: cr = circle radius:25; addModifier cr (Edit_Spline()).
При выводе кривые аппроксимируются отрезками прямых. Так, в 3ds Max окружность имеет свойство Steps, регулирующее число аппроксимирующих отрезков (рис. 1.4).
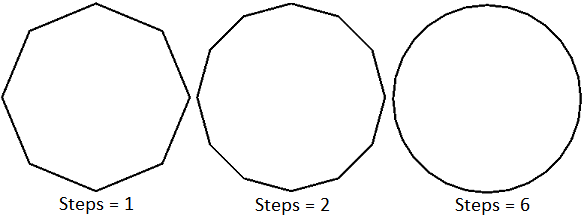
Рис. 1.4. Аппроксимация окружности отрезками прямой
Задания.
Написать программы, выполняющие следующие действия:
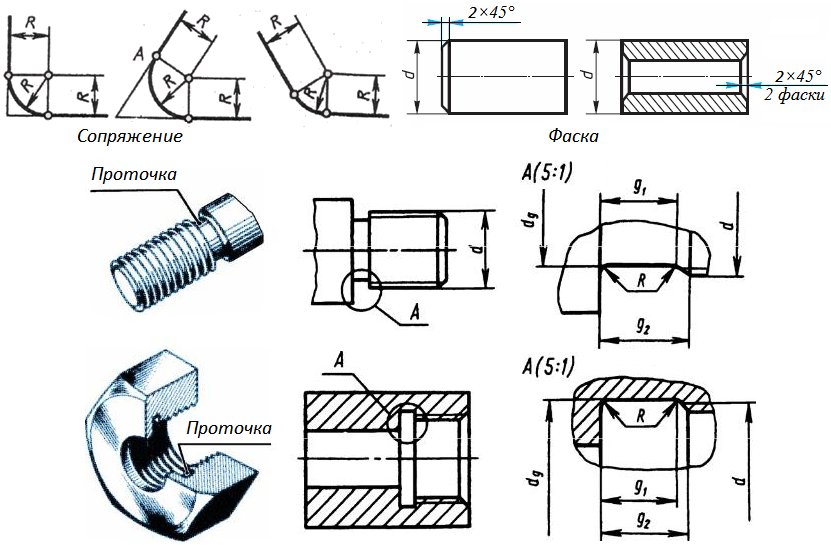
Рис. 1.5. Сопряжения, фаски и проточки
Замечание. При построениях используется инструмент "Объектная привязка", который может употреблен, например, для проведения перпендикуляров, медиан или касательных.
3d полигональная модель может быть создана в результате преобразования 3d-примитивов, например, таких, как
Имеется немало инструментов для построения 3d-объектов. Работу можно вести на уровнях вершин, ребер и полигонов. Часто употребляемые преобразования оформляются в приложениях в виде соответствующих инструментов.
Так, в 3ds Max модель пуговицы (рис. 1.6) можно создать в результате объединения трубы и цилиндра и последующего вычитания из суммарного объекта четырех цилиндров.
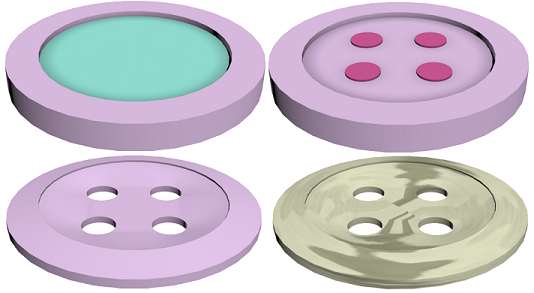
Рис. 1.6. Создание пуговицы
Употребленный далее модификатор Relax сглаживает образ. На завершающем этапе объекту назначается материал с текстурой Marble.
На MaxScript приведенная последовательность действий реализуется следующим кодом:
delete $*
r1 = 60 -- Внешний радиус трубы
r2 = 45 -- Внутренний радиус трубы, он же радиус большого цилиндра
r3 = 8 -- Радиус малого цилиндра
h = 10 -- Высота большого цилиндра
nHls = 4 -- Число отверстий(как вариант, nHls = 2)
d = 0.5 * r2 -- Определяет положение отверстий
-- Создаем трубу, большой цилиндр и их сумму
tb = tube pos:[0, 0, 0] radius1:r1 radius2:r2 height:(h + 3) sides:36
cl = cylinder pos:[0, 0, 0] radius:r2 height:h sides:36
proBoolean.createBooleanObjects tb cl 0 2 0 -- Union
-- Создаем и перемещаем малые цилиндры и их сумму и их разность с прежним объектом
arrCl = for k = 1 to nHls collect cylinder pos:[0, 0, -1] radius:r3 height:(h + 2) sides:36
move arrCl[1] [-d, 0, 0]
move arrCl[2] [d, 0, 0]
if nHls == 4 do (
move arrCl[3] [0, -d, 0]
move arrCl[4] [0, d, 0]
)
proBoolean.createBooleanObjects tb arrCl 2 2 0 -- Subtraction
-- Употребляем модификатор Relax и назначаем объекту материал с текстурой Marble
rlx = relax relax_Value:1
addModifier tb rlx
addModifier tb (UVWmap maptype:1 cap:off) -- Генерируем координаты текстуры
mbl = marble()
mbl.coords.tiling = [5, 5, 1]
std = standard diffuseMap:mbl showInViewPort:on
tb.material = std
Часть банки (или банку целиком) можно получить, вращая плоскую фигуру вокруг вертикальной оси (рис. 1.7).

Рис. 1.7. Пример поверхности вращения
В 3ds Max такой результат получается после выполнения следующего MaxScript-кода:
delete $*
-- Создаем плоскую фигуру
sp = line wireColor:(color 135 110 8) transform:(matrix3 [1,0,0] [0,0,1] [0,-1,0] [0,0,0])
addNewSpline sp
arrV = #([0, 0, 0], [40, 0, 0], [80, 0, 90], [100, 0, 90], [50, 0, -20], [0, 0, -20])
for i = 1 to arrV.Count do (addKnot sp 1 #corner #line arrV[i])
close sp 1
updateShape sp
-- Создаем модификатор Lathe
lth = lathe degrees:120.0 capStart:true capEnd:true
-- Получаем поверхность вращения
addModifier sp lth
Такие поверхности создаются в результате перемещения одного сплайна вдоль другого.
В 3ds Max для этих целей можно употребить, например, модификатор Sweep или объект Loft.
На рис. 1.8 показаны двутавровый профиль и изогнутая труба, созданная как Loft-объект.

Рис. 1.8. Пример поверхностей сдвига (смещения)
Sweep-профиль получается после запуска следующего MaxScript-кода:
delete $*
-- Создаем направляющую линию
sp = line()
sp.Wirecolor = color 135 110 8
addNewSpline sp
addKnot sp 1 #corner #line [-40, 0, 0]
addKnot sp 1 #corner #line [40, 30, 0]
updateShape sp
-- Создаем и применяем модификатор Sweep
swp = sweep()
addModifier sp swp
swp.CurrentBuiltInShape = 10 -- WideFlange-секция
swp[#Wide_Flange_Section].Wide_flange_length = 15
swp[#Wide_Flange_Section].Wide_flange_width = 10
swp[#Wide_Flange_Section].Wide_flange_thickness = 2
Loft-труба получает в результате перемещения окружности по сплайну, так же показанных на рис. 1.8.
Многие графические приложения позволяют располагать компоненты рисунка на разных слоях. Слой имеет следующие свойства:
Наличие в рисунке слоев добавляет новые возможности. В частности, в системе проектирования печатных плат PCAD в подсистеме проектирования принципиальных электрических схем следующие компоненты:
располагаются на разных слоях (рис. 1.9).
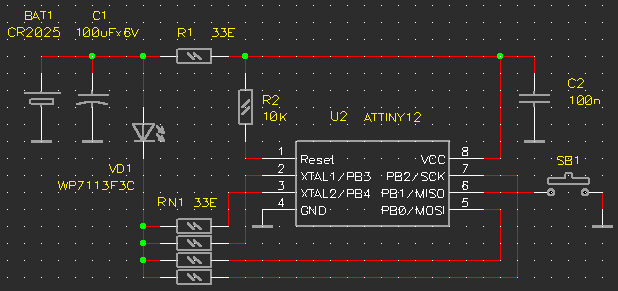
Рис. 1.9. PCAD: рисунок принципиальной электрической схемы
Кроме того, каждый из указанных видов компонентов является блоком с текстовыми атрибутами. Это позволяет, в частности, автоматически генерировать список соединений схемы по ее рисунку.
База данных рисунка хранит сведения о рисунке в целом (текущая матрица проецирования, списки объектов т. д.) и его отдельных объектах - примитивах, материалах, источниках цвета, камерах и т. д.
Рассмотрим, к примеру, описание примитивов в ранних версиях Автокада. Подобные описания можно получить, задав, например, в командной строке приложения (entget (entlast)) после ввода очередного примитива.
Так, для линии получим следующий список списки точечных пар:
((-1 .<Имя примитива: 60000044>)
(0 . "LINE") ; Тип примитива
(6 . "DASHED") ; Тип линии
(8 . "NEW") ;Имя слоя, на котором расположен примитив
(62 . 3) ; Способ задания цвета (0 - по блоку; 256 - по слою)
(10 . 20.0 10.0 0.0) ; Начальная точка линии (отрезка)
(11 . 200.0 100.0 0.0) ; Конечная точка линии (отрезка)
(210 . 0.0 0.0 1.0) ; Направление выдавливания
)
В случае текста имеем следующий список точечных пар:
((-1 . <Имя примитива: 60000066>)
(0 . "TEXT") ; Тип примитива
(6 . "DASHED") ; Тип линии
(8 . "NEW") ; Имя слоя, на котором расположен примитив
(62 . 3) ; Способ задания цвета (0 - по блоку; 256 - по слою)
(10 . 20.0 10.0 0.0) ; Начальная точка текста
(1 . "This is a text") ; Выводимый текст
(50 . 0.785398) ; Угол поворота в радианах
(41 . 1) ; Коэффициент растяжения
(51 . 0.523599) ; Угол наклона в радианах
(7 . "ITALICC") ;Гарнитура шрифта
(71 . 0) ; Флаг генерации; отображается ли текст в обратном порядке (backwards) или перевернутым (upside-down)
(72 . 0) ; Тип выравнивания текста по строке текста
(11 . 0.0 0.0 0.0) ; Точка, относительно которой выполняется выравнивания
(210 . 0.0 0.0 1.0) ; Направление выдавливания
(73 . 0) ;Тип выключки - способ выравнивания в направлении, перпендикулярном строке текста
)
В 3ds Max компоненты рисунка - это объекты, обладающие свойствами и в некоторых случаях методами. Так, сфера имеет следующие свойства:

Рис. 1.10. Сфера: два способа воспроизведения (сглаженная и без сглаживания)
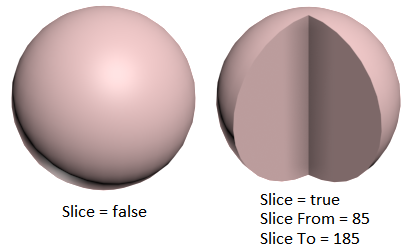
Рис. 1.11. Сфера: свойства Slice, SliceFrom и SliceTo
Многие свойства, например Radius, Segs, SliceFrom и SliceTo, можно анимировать, то есть изменять от кадра к кадру.
Кроме того, сфера наследует свойства, общие для 3d-объектов приложения, например Material, Parent и Mesh.
Как вариант, база данных рисунка может быть основана на реляционной модели, что позволит искать и выбирать данные средствами SQL.
Пример такой организации данных можно посмотреть в работе Разработка базы данных для представления анимированной модели 3d–объекта.
Схема преобразования координат (на примере OpenGL) показана на рис. 2.1.
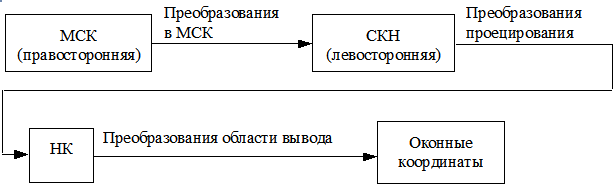
Рис. 2.1. Схема преобразования координат
Координаты отображаемых объектов (примитивов) задаются в мировой системе координат (МСК).
В ней над объектами выполняются аффинные преобразования.
Система координат, в которой задается матрица проецирования, называется системой координат наблюдателя (СКН).
В ней рассчитываются цвета объектов и выполняются заданные отсечения.
Далее под воздействием матрицы проецирования координаты СКН переводятся в нормированные координаты (НК). Диапазон их изменения - [-1.0, 1.0].
С окном вывода связывается оконная система координат (ОСК), в которой осуществляется вывод объектов.
Непосредственно перед выводом нормированные координаты преобразовываются в оконные.
В 3ds Max матрица аффинных преобразованний возвращается свойством transform.
В примере эта матрица выводится после создания объекта (сферы) и затем после выполнения аффинных преобразований переноса, поворота и масштабирования:
delete $*
sp = sphere radius:25
sp.transform -- (matrix3 [1,0,0] [0,1,0] [0,0,1] [0,0,0])
move sp [10, 9, 8]
sp.transform -- (matrix3 [1,0,0] [0,1,0] [0,0,1] [10,9,8])
rotate sp (angleaxis 45 [1,0,0])
sp.transform -- (matrix3 [1,0,0] [0,0.707107,0.707107] [0,-0.707107,0.707107] [10,9,8])
scale sp [0.5, 0.5, 0.5]
sp.transform -- (matrix3 [0.5,0,0] [0,0.353553,0.353553] [0,-0.353553,0.353553] [10,9,8])
Те же аффинные преобразования можно произвести, изменив свойство transform объекта:
delete $*
sp = sphere radius:25
sp.transform = matrix3 [0.5,0,0] [0,0.353553,0.353553] [0,-0.353553,0.353553] [10,9,8]
С окном вывода, задаваемого на экране монитора, связана физическая система координат (ФСК), определяемая техническими средствами.
Начало ФСК - левый верхний угол экрана.
Ось абсцисс направлена слева направо; ось ординат - сверху вниз (рис. 2.2).
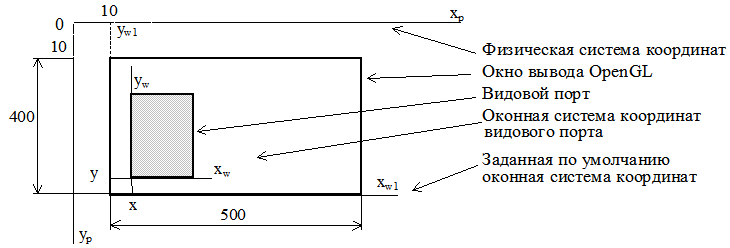
Рис. 2.2. Физическая и оконная системы координат
Единицы измерения координат - пиксели экрана, поэтому физические координаты целочисленные.
Наименьшие координаты пикселя xmin = 0 и ymin = 0.
Наибольшие координаты определяются установленным разрешением. Так, при разрешении 800×600 пикселей наибольшие координаты пикселя xmax = 799 и ymax = 599.
В ФСК задаются координаты верхнего левого угла окна графических данных и его размеры в пикселях
Вывод графических данных осуществляется в экранно-ориентированную прямоугольную область графического окна вывода.
Такая область называется видовым портом. С ним связана ОСК.
Начало ОСК находится в нижнем левом углу видового порта (см. рис. 2.2). Задаваемые относительно начала ОСК координаты называются оконными.
Преобразование координат области вывода, переводящие нормированные координаты xnd, ynd в оконные координаты xw, yw, выполняются по формулам:
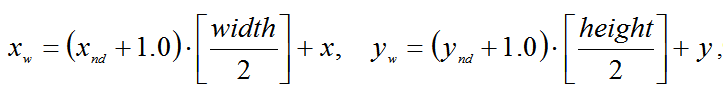
где width и height - ширина и высота видового порта в пикселях; x, y - координаты нижнего левого угла видового порта; [a] - целая часть числа a.
Координаты вершин графических объектов нередко задают в локальной системе координат, начало которой расположено в так называемой базовой точке.
При отображении объекта координаты пересчитываются в мировые, после чего реализуется вышеприведенная схема преобразования координат.
В 3ds Max мировые координаты вершины полигонального объекта можно получить, например, следущим образом:
delete $*
sp = sphere radius:30 pos:[0, 0, 0] -- Создаем сферу в начале мировой системы координат
move sp [-15, -10, 7] -- Перемещаем сферу
v1 = sp.mesh.verts[1] -- Первая вершина сферы
v1_local = v1.pos -- [0, 0, 30] - локальные координаты первой вершины
-- Умножаем локальные координаты на матрицу аффинных преобразований сферы
v1_world = v1_local * sp.transform -- [-15, -10, 37] - мировые координаты первой вершины
При этом матрица аффинных преобразований сферы такова:
(matrix3 [1,0,0] [0,1,0] [0,0,1] [-15,-10,7])
По умолчанию базовая точка сферы находится в ее центре (рис. 2.3).
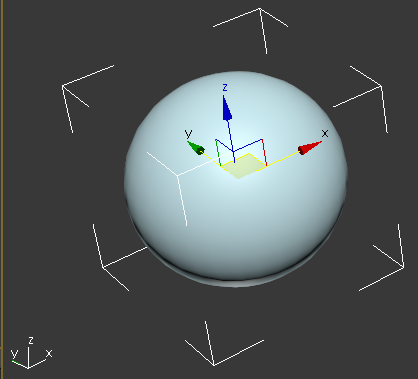
Рис. 2.3. Сфера и ее локальная система координат
В нижнем левом углу рисунка показаны орты мировой системы координат.
Из аналитической геометрии известно, что любые преобразования координат на плоскости можно выполнить в результате следующих преобразований, называемых аффинными:
Формулы аффинных преобразований.
В формулах x и y - координаты до преобразований, а x* и y* - после преобразований.
Преобразование переноса нельзя записать в виде матрицы 2×2. Поэтому, чтобы все виды аффинных преобразований записать в виде матриц, используются однородные координаты: произвольной точке M(x, y) плоскости ставится в соответствие точка M*(x, y, 1) в пространстве. Это позволяет записать аффинные преобразования на плоскости в виде матриц 3×3.
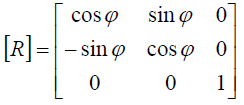
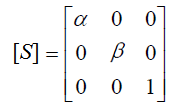
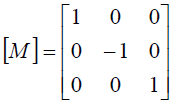
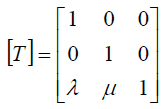
Результирующие координаты вершины, например после поворота, вычисляются по следующей формуле:
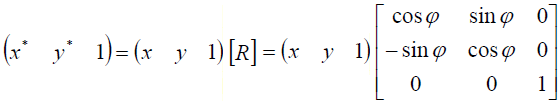
Задания.
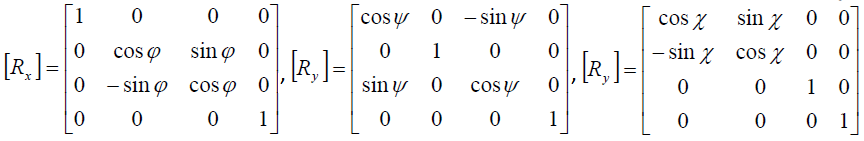
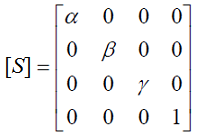
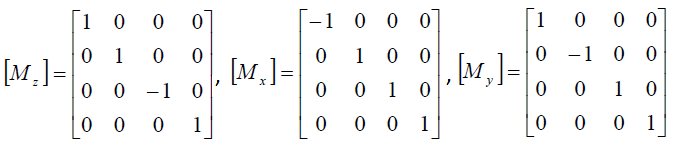
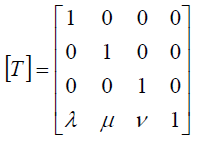
Задания.
Рассмотрим пример, в котором, используя средства графической библиотеки OpenGL, кубик перемещается по окружности и одновременно вращается вокруг оси аппликат локальной системы координат, показанной на рис. 2.4.
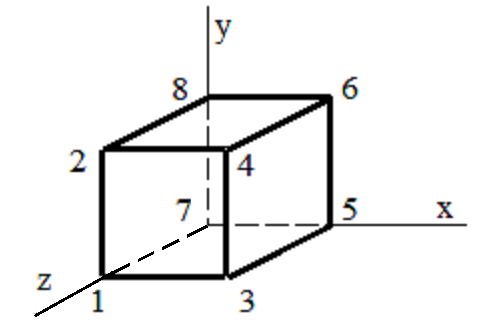
Рис. 2.4. Локальная система координат куба
Программа, реализующая заданную последовательность преобразований, написана на C#.
Анимация выполняется при помощи объекта Timer, срабатывающего каждые 100 миллисекунд. После каждого тика таймера в конечном итоге формируются матрицы переноса и вращения, действующие на все вершины куба и определяющие его новое положение (рис. 2.5).
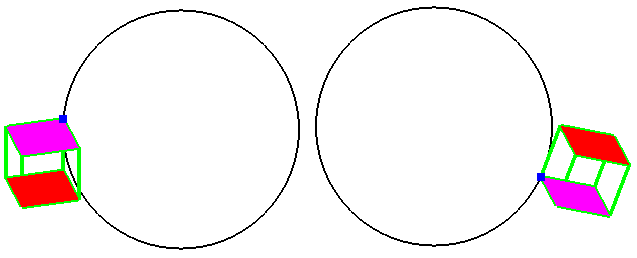
Рис. 2.5. Движение куба по окружности
Боковые грани куба выведены как линии, а нижняя и верхняя залиты текущим цветом.
Приведены 2 варианта программы - первый использует библиотеку Tao, второй - OpenTK.
Как подключить Tao, можно посмотреть, например, в Программная имитация эксперимента по определению ускорения свободного падения.
Там же показано, как подключить таймер (в свойствах таймера следует для Enabled указать true, событию Tick назначить обработчик timer1_Tick).
В случае OpenTK таймер не используется. Поворот куба на заданный угол выполняется после нажатия на F11.
Первоначально куб выводится в центре окружности (пути). Перемещение куба на окружность произойдет после первого нажатия на F11.
Как обеспечить доступ к OpenTK показано, например, в OpenTK: вывод частиц.
// Используем Tao
using System;
using System.Windows.Forms;
// Для работы с библиотекой OpenGL
using Tao.OpenGl;
// Для работы с элементом управления SimpleOpenGLControl
using Tao.Platform.Windows;
namespace WindowsFormsApplication1
{
public partial class Form1 : Form
{
double w = 300, h = 250; // Параметры матрицы ортогонального проецирования
double radius = 150; // Радиус окружности
double edge = 75; // Длина ребра куба
double [] baseCrrnt = { 0, 0, 0 }; // Мировые координаты базовой точки куба (начала его локальной системы координат)
double ax = 30; // Угол поворота куба относительно оси X (не меняется)
double ay = 15; // Угол поворота куба относительно оси Y (не меняется)
double az = 0; // Угол поворота куба относительно оси Z
double dz = 5; // az = az + dz
double baseAngle = 0; // Угол поворота базовой точки куба относительно оси Z
double df = 5; // baseAngle = baseAngle + df
double pi180 = Math.PI / 180.0;
double pi2 = Math.PI * 2.0;
// cwh - коэффициент изменения параметров проецирования
double cwh = 0.975; // w = w * cwh; h = h * cwh;
bool dcr = true;
public Form1()
{
InitializeComponent();
CG2.InitializeContexts(); // CG2 – имя окна OpenGL
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
}
// Вывод куба и траектории
private void drawCube(double w, double h, double ax, double ay, double az, double [] baseCrrnt, bool pth)
{
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
Gl.glMatrixMode(Gl.GL_MODELVIEW);
Gl.glLoadIdentity();
if (pth)
{
// Вывод пути (окружности)
Gl.glColor3d(0.0, 0.0, 0.0); // Текущий цвет черный
double ngl = 0;
double x = 0, y = radius;
Gl.glVertex3d(x, y, 0);
Gl.glLineWidth(2); // Толщина линии
Gl.glBegin(Gl.GL_LINES); // Вывод линий, аппроксимирующих окружность
while (ngl < 10)
{
ngl += df * pi180;
double x2 = radius * Math.Sin(ngl);
double y2 = radius * Math.Cos(ngl);
Gl.glVertex3d(x, y, 0);
Gl.glVertex3d(x2, y2, 0);
x = x2;
y = y2;
}
Gl.glEnd(); // Заканчиваем вывод пути
}
// Формируем матрицу преобразования координат куба
// Матрица переноса
Gl.glTranslated(baseCrrnt[0], baseCrrnt[1], baseCrrnt[2]);
// Матрица вращения
Gl.glRotated(ax, 1.0, 0.0, 0.0); // Поворот вокруг оси Х на угол ax против часовой стрелки
Gl.glRotated(ay, 0.0, 1.0, 0.0); // Поворот вокруг оси Y на угол ay против часовой стрелки
Gl.glRotated(az, 0.0, 0.0, 1.0); // Поворот вокруг оси Z на угол az против часовой стрелки
Gl.glMatrixMode(Gl.GL_PROJECTION); // Текущей стала матрица проецирования
Gl.glLoadIdentity();
Gl.glOrtho(-w, w, -h, h, -w, w); // Матрица ортографического проецирования
Gl.glShadeModel(Gl.GL_FLAT);
Gl.glLineWidth(4); // Толщина линии
Gl.glPolygonMode(Gl.GL_FRONT_AND_BACK, Gl.GL_LINE);
Gl.glBegin(Gl.GL_QUAD_STRIP); // Вывод боковых граней
Gl.glColor3d(0.0, 1.0, 0.0); // Текущий цвет зеленый
Gl.glVertex3d(0.0, 0.0, edge); // 1 - номер вершины куба
Gl.glVertex3d(0.0, edge, edge); // 2
Gl.glVertex3d(edge, 0.0, edge); // 3
Gl.glVertex3d(edge, edge, edge); // 4
Gl.glVertex3d(edge, 0.0, 0.0); // 5
Gl.glVertex3d(edge, edge, 0.0); // 6
Gl.glVertex3d(0.0, 0.0, 0.0); // 7
Gl.glVertex3d(0.0, edge, 0.0); // 8
Gl.glVertex3d(0.0, 0.0, edge); // 1
Gl.glVertex3d(0.0, edge, edge); // 2
Gl.glEnd();
// Заливаем нижнюю и верхнюю грани текущим цветом
Gl.glPolygonMode(Gl.GL_FRONT_AND_BACK, Gl.GL_FILL);
Gl.glBegin(Gl.GL_QUADS); // Вывод нижней и верхней граней
Gl.glColor3d(1.0, 0.0, 1.0); // Фиолетовый цвет для нижней грани
Gl.glVertex3d(0.0, 0.0, 0.0); // 1 - номер вершины куба
Gl.glVertex3d(edge, 0.0, 0.0); // 3
Gl.glVertex3d(edge, 0.0, edge); // 5
Gl.glVertex3d(0.0, 0.0, edge); // 7
Gl.glColor3d(1.0f, 0.0, 0.0); // Красный цвет для верхней грани
Gl.glVertex3d(0.0, edge, 0.0); // 2
Gl.glVertex3d(edge, edge, 0.0); // 4
Gl.glVertex3d(edge, edge, edge); // 6
Gl.glVertex3d(0.0, edge, edge); // 8
Gl.glEnd(); // Заканчиваем вывод верхней грани
Gl.glPointSize(8); // Размер точки
Gl.glBegin(Gl.GL_POINTS); // Вывод начала координат
Gl.glColor3d(0.0, 0.0, 1.0); // Синий цвет
Gl.glVertex2f(0, 0f);
Gl.glEnd(); // Заканчиваем вывод начала координат
Gl.glFlush(); // Отображаем примитивы на экране
CG2.Invalidate();
}
// Обработчик срабатывания таймера. По умолчанию таймер срабатывает каждые 100 миллисекунд
private void timer1_Tick(object sender, EventArgs e)
{
nextFrame(ref baseCrrnt, ref az); // Текущие координаты базовой точки и угол поворота кубика
drawCube(w, h, ax, ay, az, baseCrrnt, true); // Отображение текущей сцены
}
// Расчет параметров, определяющих координаты вершин куба
private void nextFrame(ref double [] baseCrrnt, ref double az)
{
// Координаты базовой точки куба
baseCrrnt[0] = radius * Math.Cos(baseAngle); // Угол в радианах
baseCrrnt[1] = radius * Math.Sin(baseAngle);
// Угол поворота базовой точки куба относительно оси Z
baseAngle += df * pi180;
if (baseAngle > pi2) baseAngle = df * pi180;
// Угол поворота куба относительно своей базовой точки
az += dz; // Угол в градусах
if (az > 360.0) az = dz;
}
}
}
// Используем OpenTK
// Первоначально куб выводится в центре окружности (пути)
// Перемещение куба на окружность произойдет после первого нажатия на F11
using System;
using System.Drawing; // Color
using OpenTK; // WindowState , Exit() and so on
using OpenTK.Graphics.OpenGL;
using OpenTK.Input; // KeyboardKeyEventArgs
namespace AffineTest
{
public class SimpleWindow : GameWindow
{
double w = 300, h = 300; // Параметры матрицы ортогонального проецирования
double radius = 150; // Радиус окружности
double edge = 75; // Длина ребра куба
double[] baseCrrnt = { 0, 0, 0 }; // Мировые координаты базовой точки куба (начала его локальной системы координат)
double ax = 30; // Угол поворота куба относительно оси X (не меняется)
double ay = 15; // Угол поворота куба относительно оси Y (не меняется)
double az = 0; // Угол поворота куба относительно оси Z
double dz = 5; // az = az + dz
double baseAngle = 0; // Угол поворота базовой точки куба относительно оси Z
double df = 5; // baseAngle = baseAngle + df
double pi180 = Math.PI / 180.0;
double pi2 = Math.PI * 2.0;
// 400 * 400 - размер окна вывода
public SimpleWindow() : base(400, 400)
{
KeyDown += Keyboard_KeyDown; // Обработчик нажатий на клавиши клавиатуры
}
// Вывод куба и траектории
private void drawCube(double w, double h, double ax, double ay, double az, double [] baseCrrnt)
{
GL.ClearColor(Color.White);
GL.Clear(ClearBufferMask.ColorBufferBit); // Очистка буфера цвета
GL.MatrixMode(MatrixMode.Modelview);
GL.LoadIdentity();
// Вывод пути (окружности)
GL.Color3(Color.Black); // Текущий цвет черный
double ngl = 0;
double x = 0, y = radius;
GL.Vertex3(x, y, 0);
GL.LineWidth(2); // Толщина линии
GL.Begin(PrimitiveType.Lines); // Вывод линий, аппроксимирующих окружность
while (ngl < 10)
{
ngl += df * pi180;
double x2 = radius * Math.Sin(ngl);
double y2 = radius * Math.Cos(ngl);
GL.Vertex3(x, y, 0);
GL.Vertex3(x2, y2, 0);
x = x2;
y = y2;
}
GL.End(); // Заканчиваем вывод пути
// Формируем матрицу преобразования координат куба
// Матрица переноса
GL.Translate(baseCrrnt[0], baseCrrnt[1], baseCrrnt[2]);
// Матрица вращения
GL.Rotate(ax, 1.0, 0.0, 0.0); // Поворот вокруг оси Х на угол ax против часовой стрелки
GL.Rotate(ay, 0.0, 1.0, 0.0); // Поворот вокруг оси Y на угол ay против часовой стрелки
GL.Rotate(az, 0.0, 0.0, 1.0); // Поворот вокруг оси Z на угол az против часовой стрелки
GL.MatrixMode(MatrixMode.Projection); // Текущей стала матрица проецирования
GL.LoadIdentity();
GL.Ortho(-w, w, -h, h, -w, w); // Матрица ортографического проецирования
GL.ShadeModel(ShadingModel.Flat);
GL.LineWidth(4); // Толщина линии
GL.PolygonMode(MaterialFace.FrontAndBack, PolygonMode.Line);
GL.Begin(PrimitiveType.QuadStrip); // Вывод боковых граней
GL.Color3(Color.Green); // Текущий цвет зеленый
GL.Vertex3(0.0, 0.0, edge); // 1 - номер вершины куба
GL.Vertex3(0.0, edge, edge); // 2
GL.Vertex3(edge, 0.0, edge); // 3
GL.Vertex3(edge, edge, edge); // 4
GL.Vertex3(edge, 0.0, 0.0); // 5
GL.Vertex3(edge, edge, 0.0); // 6
GL.Vertex3(0.0, 0.0, 0.0); // 7
GL.Vertex3(0.0, edge, 0.0); // 8
GL.Vertex3(0.0, 0.0, edge); // 1
GL.Vertex3(0.0, edge, edge); // 2
GL.End();
// Заливаем нижнюю и верхнюю грани текущим цветом
GL.PolygonMode(MaterialFace.FrontAndBack, PolygonMode.Fill);
GL.Begin(PrimitiveType.Quads); // Вывод нижней и верхней граней
GL.Color3(Color.Magenta); // Фиолетовый цвет для нижней грани
GL.Vertex3(0.0, 0.0, 0.0); // 1 - номер вершины куба
GL.Vertex3(edge, 0.0, 0.0); // 3
GL.Vertex3(edge, 0.0, edge); // 5
GL.Vertex3(0.0, 0.0, edge); // 7
GL.Color3(Color.Red); // Красный цвет для верхней грани
GL.Vertex3(0.0, edge, 0.0); // 2
GL.Vertex3(edge, edge, 0.0); // 4
GL.Vertex3(edge, edge, edge); // 6
GL.Vertex3(0.0, edge, edge); // 8
GL.End(); // Заканчиваем вывод верхней грани
GL.PointSize(8); // Размер точки
GL.Begin(PrimitiveType.Points); // Вывод начала координат
GL.Color3(Color.Blue); // Синий цвет
GL.Vertex2(0, 0f);
GL.End(); // Заканчиваем вывод начала координат
}
// Обработчик нажатий на клавиши клавиатуры
void Keyboard_KeyDown(object sender, KeyboardKeyEventArgs e)
{
if (e.Key == Key.Escape) this.Exit();
if (e.Key == Key.F11)
nextFrame(ref baseCrrnt, ref az); // Текущие координаты базовой точки и угол поворота кубика
}
// Расчет параметров, определяющих координаты вершин куба
private void nextFrame(ref double [] baseCrrnt, ref double az)
{
// Координаты базовой точки куба
baseCrrnt[0] = radius * Math.Cos(baseAngle); // Угол в радианах
baseCrrnt[1] = radius * Math.Sin(baseAngle);
// Угол поворота базовой точки куба относительно оси Z
baseAngle += df * pi180;
if (baseAngle > pi2) baseAngle = df * pi180;
// Угол поворота куба относительно своей базовой точки
az += dz; // Угол в градусах
if (az > 360.0) az = dz;
}
protected override void OnLoad(EventArgs e)
{
GL.ClearColor(Color.White);
GL.Viewport(0, 0, 600, 600);
// Формируем матрицу проецирования
GL.MatrixMode(MatrixMode.Projection);
GL.LoadIdentity();
GL.Ortho(-w, w, -h, h, -w, w);
}
// Выполняется при воспроизведении кадра изображения
protected override void OnRenderFrame(FrameEventArgs e)
{
GL.Clear(ClearBufferMask.ColorBufferBit);
GL.Viewport(0, 0, Width, Height);
drawCube(w, h, ax, ay, az, baseCrrnt); // Отображение текущей сцены
this.SwapBuffers();
}
// Entry point
[STAThread]
public static void Main()
{
using (SimpleWindow affine = new SimpleWindow())
{
affine.Title = "Аффинные преобразования";
affine.Run(30.0, 0.0);
}
}
}
}
Проецирование, или проектирование, - это отображение на плоскости пространственной фигуры при помощи лучей, проходящих через вершины фигуры.
Если все проецирующие прямые выходят из одной точки, то проецирование называется центральным, или перспективным, а точка, из которой выходят лучи, называется центром проецирования (рис. 2.6).
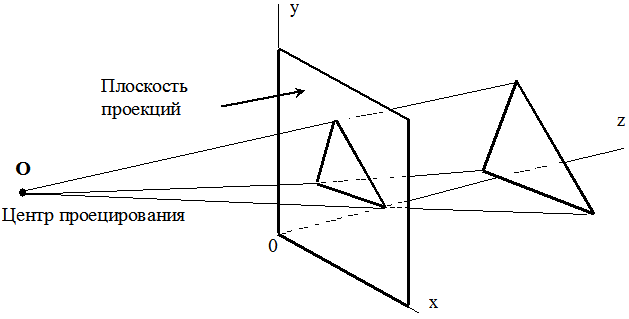
Рис. 2.6. Перспективное проецирование
Если же центр проецирования находится на бесконечно большом расстоянии от плоскости проекций, проецирующие лучи параллельны друг другу, то мы имеем параллельное проецирование.
Если проецирующие лучи вдобавок перпендикулярны плоскости проекций, то проецирование называется прямоугольным, или ортографическим.
На рис. 2.7 показаны прямоугольные проекции на фронтальную, горизонтальную и профильную плоскости проекций.
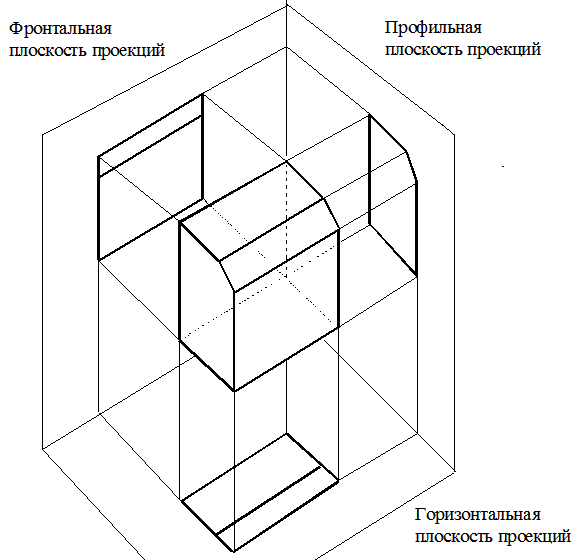
Рис. 2.7. Ортографическое проецирование
В OpenGLматрица прямоугольного проецирования задает объем вывода в виде прямоугольного параллелепипеда (рис. 2.8): все объекты или их части, находящиеся в этом объеме, будут отображены в видовом порте.
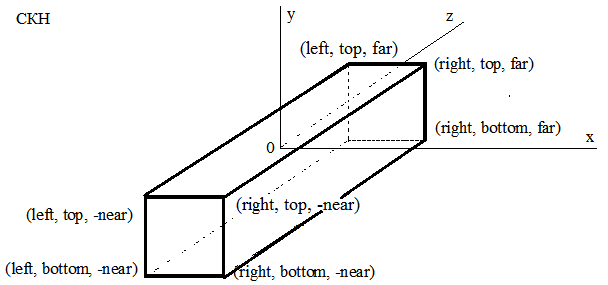
Рис. 2.8. Интерпретация матрицы прямоугольного проецированияOpenGL (задается в СКН)
Матрица записывается следующим образом:
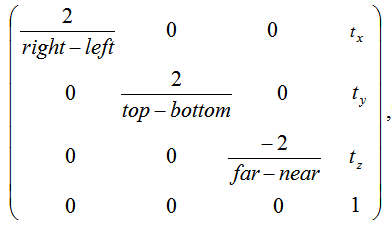
где
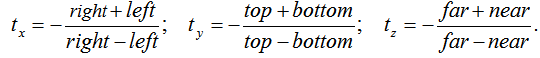
После выполнения преобразования проецирования формируется трехмерная область видимости с ортогональным базисом SxSySz:
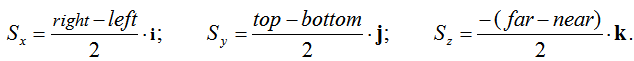
Координаты центра области видимости:
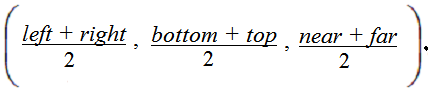
Формируемый базис является левосторонним (в отличие от базиса МСК, который является правосторонним); после преобразования ортографического проецирования координаты любых точек внутри преобразованной трехмерной области видимости находятся в диапазоне от -1 до 1. То есть преобразованная область видимости представляет собой куб со стороной, равной двум.
Напомним, что координаты, полученные в результате преобразования проецирования, называются нормированными.
Матрица ортографического проецирования задается следующей процедурой:
Gl.glOrtho(left, right, bottom, top, near, far);
Графический образ будет более информативен, если использовать аксонометрическое проецирование. Для полноты восприятия 3d-объекта его располагают его перед одной из плоскостей проекций так, чтобы он был виден сразу с трех сторон: спереди, сверху и слева. А затем выполняется параллельное проецирование объекта на выбранную плоскость проекций (более подробно см. в работе OpenGL: преобразование координат).
На рис. 2.9 показаны две проекции куба: выполняется изменение параметров матрицы проецирования, приближающее (удаляющее) наблюдателя от образа (аналог команды ZOOM в Автокаде).
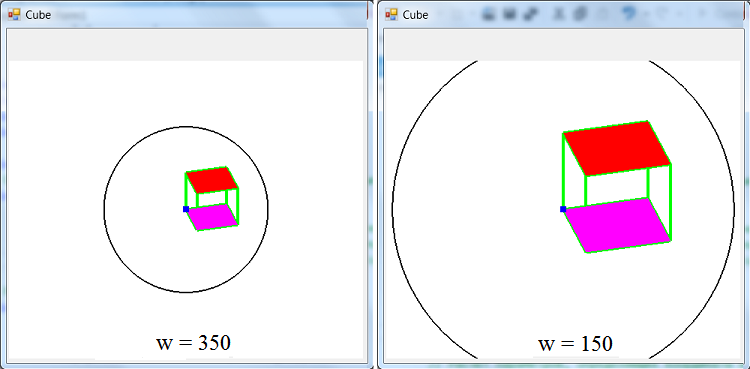
Рис. 2.9. Куб в большой и малой области видимости
Результат получен после внесения в вышеприведенную программу (в варианте Tao) следующих изменений:
// Обработчик срабатывания таймера. По умолчанию таймер срабатывает каждые 100 миллисекунд
private void timer1_Tick(object sender, EventArgs e)
{
//nextFrame(ref baseCrrnt, ref az); // Текущие координаты базовой точки и угол поворота кубика
nextFrame2(ref w, ref h); // Текущие значения параметров матрицы проецирования
drawCube(w, h, ax, ay, az, baseCrrnt, true); // Отображение текущей сцены
}
// Изменение параметров матрицы проецирования
private void nextFrame2(ref double w, ref double h)
{
if (dcr && w <= 150) dcr = false;
if (!dcr && w >= 350) dcr = true;
if (dcr)
{
w *= cwh;
h *= cwh;
}
else
{
w /= cwh;
h /= cwh;
}
}
Аналогичным образом можно проиллюстрировать параномирование (в Автокаде команда PAN).
Перспективное проецирование можно организовать, в частности, оперируя одной, двумя (рис. 2.10) или тремя точками схода, расположенными на осях координат.
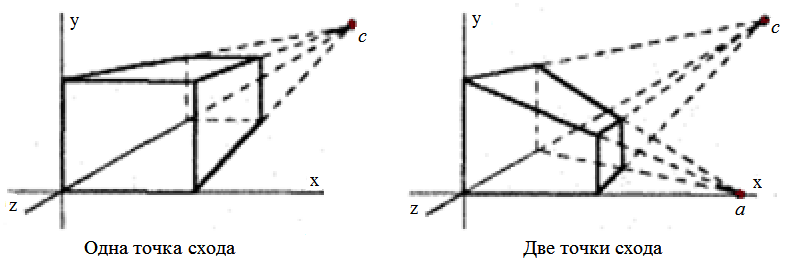
Рис. 2.10. Перспективное проецирование с одной и двумя точками схода
Матрицы перспективных преобразований с одной, двумя и тремя точками схода имеют следующий вид:
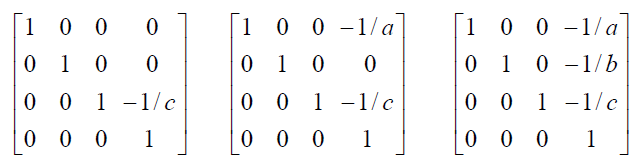
где
a, b и c - соответственно координаты точек схода на осях X, Yи Z.
На рис. 2.11 показана одноточечная проекция куба.
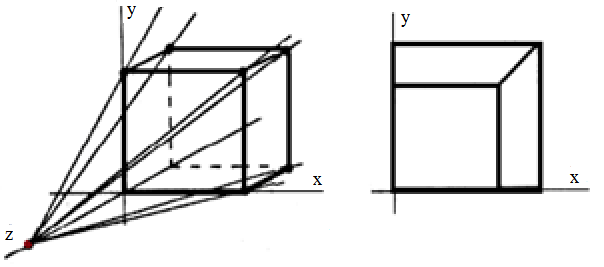
Рис. 2.11. Проекция куба с центром проекции на оси Z
На практике такие матрицы не употребляются, поскольку при проецировании должен быть выполнен переход из СКН в НК.
Это обеспечивает, в частности, следующая матрица одноточечного перспективного проецирования (проецирование с одной точкой схода):

Смысл параметров описан при рассмотрении матрицы ортографического проецирования.
Соответствующее преобразование координат обеспечивает следующая процедура OpenGL:
Gl.glFrustum(left, right, bottom, top, near, far);
Задание.
Вычислить координаты точки пересечения прямой, проходящей через центр проецирования и точку (x, y, z) (рис. 2.12), с плоскостью XY.
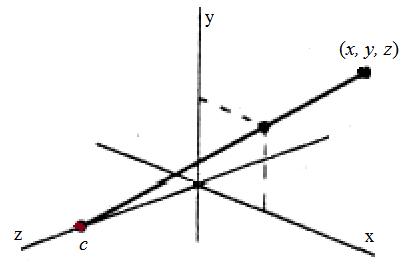
Рис. 2.12. Центральное проецирование точки (x, y, z)
Использовать параметрические уравнения прямой: x* = xt, y* = yt, z* = с + (z - c)t.
Изображение выводится на растровый экран - двумерный массив пикселей (рис. 3.1).
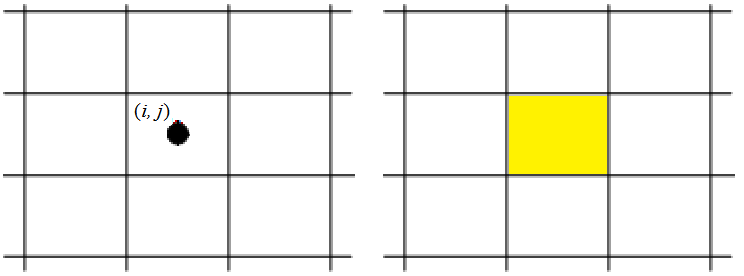
Рис. 3.1. Модель растрового экрана
При инициализации точки с координатами (i, j) закрашивается соответствующая ячейка сетки (пиксель, или видеопиксель).
Линия может быть реализована с использованием 4-соседей или 8-соседей (рис. 3.2).

Рис. 3.2. 4-соседи и 8-соседи
Четырехсвязная и восьмисвязные развертки отрезка показаны на рис. 3.3.
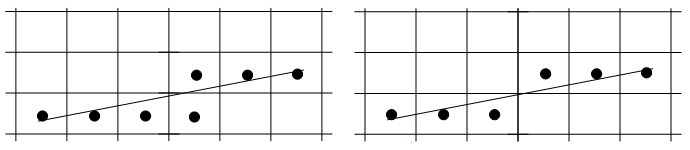
Рис. 3.3. Четырехсвязная и восьмисвязные растровые развертки отрезка
При переводе векторных данных в растровые решаются следующие задачи:
Растровое представление отрезка формируется на основе алгоритма Брезенхейма (см., например, работу Реализация схемы наложения текстуры).
Задача отсечения, иллюстрируемая рис. 3.4, рассмотрена в работе Фортран-реализация алгоритма отсечения Коэна-Сазерленда (Cohen-Sutherland).
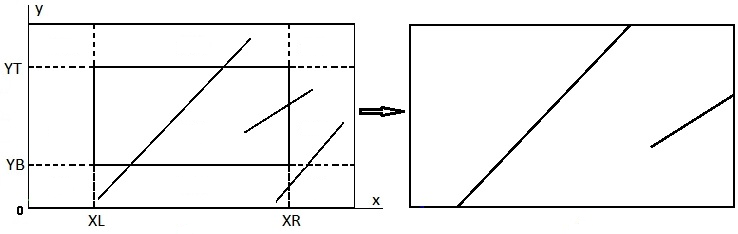
Рис. 3.4. Вывод выделенной области во всем видовом порте
Вопросы заполнения замкнутых контуров (рис. 3.5) частично рассмотрены в следующих работах:
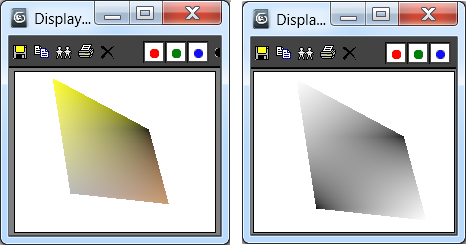
Рис. 3.5. Интерполяционная развертка полигона с различными значения цвета вершин
Пример из последней работы показан на рис. 3.6.
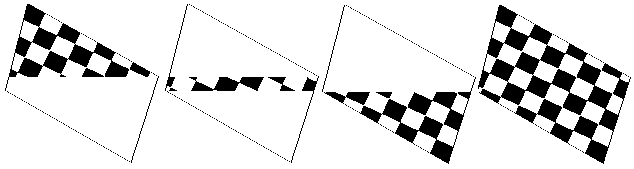
Рис. 3.6. Три этапа наложения текстуры и конечный результат
Задача загораживания на основе Z-буфера рассмотрена в работе Реализация метода Z-буфера удаления невидимых частей поверхности.
Задания.
Написать программы, реализующие следующие алгоритмы:
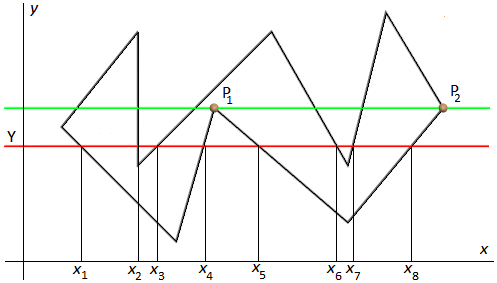
Рис. 3.7. Растровая развертка невыпуклого многоугольника
Согласно рис. 3.7 на каждой линии Y нужно выполнить следующие действия:
Описывается следующим векторным параметрическим уравнением:
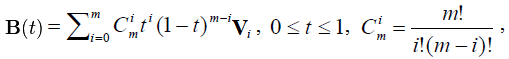
где V0, V1, …Vm - контрольные вершины (рис. 4.1).
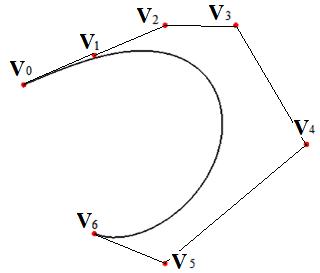
Рис. 4.1. Кривая Безье шестой степени
Ломаная V0, V1, …Vm называется контрольной ломаной.
Для вывода приведенной кривой употреблен следующий C#- код:
using System;
using System.Windows.Forms;
// Для работы с библиотекой OpenGL
using Tao.OpenGl;
// Для работы с элементом управления SimpleOpenGLControl
using Tao.Platform.Windows;
namespace WindowsFormsApplication3
{
public partial class Form1 : Form
{
// Массив контрольных вершин
double [,] V = {{0, 60, 0}, {20, 70, 0}, {40, 80, 0}, {60, 80, 0}, {80, 40, 0}, {40, 0, 0}, {20, 10, 0}};
int m = 7;
public Form1()
{
InitializeComponent();
CG2.InitializeContexts(); // CG2 – имя окна OpenGL
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
}
private void button1_Click(object sender, EventArgs e)
{
drawCurve();
}
// Вывод кривой Безье
private void drawCurve()
{
double dt = 0.02;
double t = 0;
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
Gl.glMatrixMode(Gl.GL_PROJECTION); // Текущей стала матрица проецирования
Gl.glLoadIdentity();
Gl.glOrtho(-10, 90, -10, 90, -1, 1); // Матрица ортографического проецирования
Gl.glEnable(Gl.GL_POINT_SMOOTH); // Сглаживание точек
Gl.glPointSize(6); // Размер точки
Gl.glColor3d(1.0, 0.0, 0.0); // Текущий цвет красный
Gl.glBegin(Gl.GL_POINTS);
for (int i = 0; i < m; i++) Gl.glVertex2d(V[i, 0], V[i, 1]);
Gl.glEnd(); // Заканчиваем вывод точек
Gl.glColor3d(0.0, 0.0, 0.0); // Текущий цвет черный
Gl.glLineWidth(2); // Толщина линии
Gl.glBegin(Gl.GL_LINES); // Вывод линий, аппроксимирующих сплайн Безье
while (t <= 1.0)
{
Gl.glVertex2d(xy(t, 0), xy(t, 1));
t += dt;
Gl.glVertex2d(xy(t, 0), xy(t, 1));
}
Gl.glEnd(); // Заканчиваем вывод линий
Gl.glFlush(); // Отображаем примитивы на экране
CG2.Invalidate();
}
// Возвращает текущую x- или y-координату кривой Безье
private double xy(double t, int j)
{
double t1 = 1.0 - t;
double [] t_m = new double [m];
double [] t1_m = new double [m];
double [] mF = new double [m];// Массив факториалов
int i = 0;
t_m[0] = 1;
t1_m[0] = 1;
mF[0] = 1;
for (i = 1; i < m; i++)
{
t_m[i] = t_m[i - 1] * t;
t1_m[i] = t1_m[i - 1] * t1;
mF[i] = mF[i - 1] * i;
}
double bt = 0;
for (i = 0; i < m; i++)
{
bt += mF[m - 1] / (mF[i] * mF[m - i - 1]) * t_m[i] * t1_m[m - i - 1] * V[i, j];
}
return bt;
}
}
}
Свойства кривой Безье:
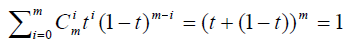
Кривая Безье целиком лежит в выпуклой оболочке, порождаемой массивом V0, V1, … Vm.
Добавление опорной точки повышает степень кривой Безье на 1.
В случае m = 3 имеем кубическую кривую Безье. Она описывается следующим векторным параметрическим уравнением:
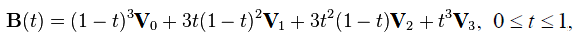
Запись кубической кривой Безье в матричной форме:
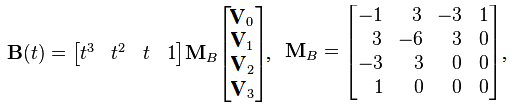
где MB - базисная матрица Безье.
При работе с кривыми Безье обнаруживаются следующие недостатки:
Замечание. Составная кривая называется G1-(геометрически) непрерывной, если вдоль этой кривой единичный вектор ее касательной изменяется непрерывно, и G2-(геометрически) непрерывной, если вдоль этой кривой изменяется непрерывно, кроме того, и вектор кривизны.
По заданному набору контрольных вершин V0, V1, V2, V3 элементарная кубическая B-сплайновая кривая задается следующим векторным параметрическим уравнением:
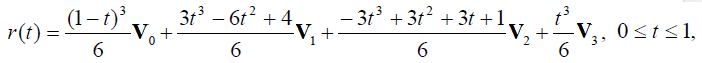
или в матричной форме r(t) = VMT, где
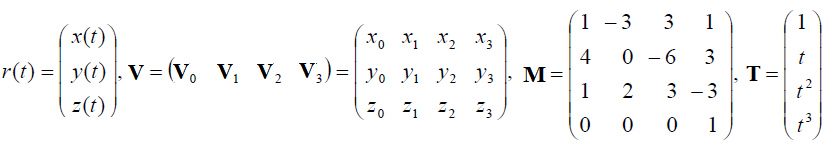
Матрица М называется базисной матрицей B-сплайновой кривой. Функциональные коэффициенты в уравнении B-сплайновой кубической кривой, неотрицательны, в сумме составляют единицу, универсальны - не зависят от координат контрольных вершин.
Это означает, что рассматриваемый элементарный фрагмент лежит внутри выпуклой оболочки заданных вершин - четырехугольника (в плоском случае, рис. 4.2) или тетраэдра (в пространственном случае).
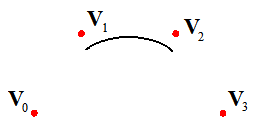
Рис. 4.2. Элементарный кубический B-сплайн
Составная кубическая B-сплайновая кривая, определяемая набором контрольных вершин
V0, V1, …, Vm-1, Vm, (m ≥ 3),
является объединением m-2 элементарных кубических B-сплайнов, которые описываются уравнениями вида
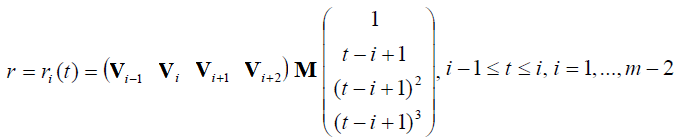
Составная B-сплайновая кубическая кривая:
При двукратном дублировании первой и последней контрольных вершин
V0 = V1 = V2 и Vm-2 = Vm-1= Vm
получим составную B-сплайновую кубическую кривую, которая начинается в V0, касаясь отрезка V0V3, и заканчивается в Vm, касаясь отрезка Vm-3Vm (рис. 4.3).
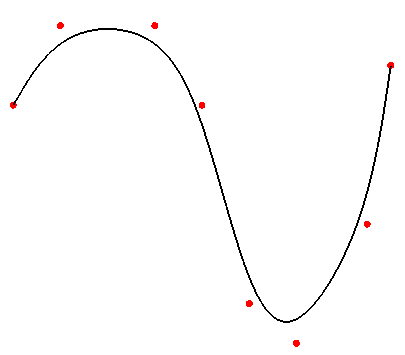
Рис. 4.3. Составной кубический B-сплайн, проходящий через первую и последнюю контрольную вершины
Чтобы получить G2-гладкий замкнутый составной кубический B-сплайн (рис. 4.4), следует первые три контрольные вершины повторить в конце набора:
Vm-2 = V0, Vm-1 = V1 и Vm = V2.
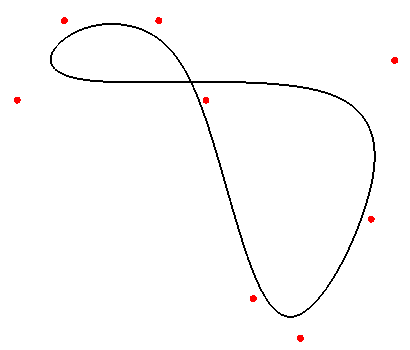
Рис. 4.4. Замкнутый составной кубический B-сплайн
Приведенный на рис. 4.4 результат обеспечивается следующим C#-кодом (при построении составного B-сплайна используется равномерная параметризация с равноотстоящими целочисленными узлами):
using System;
using System.Windows.Forms;
// Для работы с библиотекой OpenGL
using Tao.OpenGl;
// Для работы с элементом управления SimpleOpenGLControl
using Tao.Platform.Windows;
namespace WindowsFormsApplication2
{
public partial class Form1 : Form
{
// Массив контрольных вершин
//double [,] V = {{0, 60, 0}, {0, 60, 0}, {0, 60, 0}, {10, 80, 0}, {30, 80, 0}, {40, 60, 0}, {50, 10, 0}, {60, 0, 0}, {75, 30, 0}, {80, 70, 0}, {80, 70, 0}, {80, 70, 0}};
double [,] V = {{0, 60, 0}, {10, 80, 0}, {30, 80, 0}, {40, 60, 0}, {50, 10, 0}, {60, 0, 0}, {75, 30, 0}, {80, 70, 0}, {0, 60, 0}, {10, 80, 0}, {30, 80, 0}};
int m = 11;
public Form1()
{
InitializeComponent();
CG2.InitializeContexts(); // CG2 - имя окна OpenGL
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
}
private void button1_Click(object sender, EventArgs e)
{
drawCurve();
}
// Вывод кривой Безье
private void drawCurve()
{
double dt = 0.02;
double t = 0;
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT);
Gl.glMatrixMode(Gl.GL_PROJECTION); // Текущей стала матрица проецирования
Gl.glLoadIdentity();
Gl.glOrtho(-10, 90, -10, 90, -1, 1); // Матрица ортографического проецирования
Gl.glEnable(Gl.GL_POINT_SMOOTH); // Сглаживание точек
Gl.glPointSize(6); // Размер точки
Gl.glColor3d(1.0, 0.0, 0.0); // Текущий цвет красный
Gl.glBegin(Gl.GL_POINTS);
// Вывод контрольных вершин; m - число контрольных вершин
for (int i = 0; i < m; i++) Gl.glVertex2d(V[i, 0], V[i, 1]);
Gl.glEnd(); // Заканчиваем вывод точек (контрольных вершин)
Gl.glColor3d(0.0, 0.0, 0.0); // Текущий цвет черный
Gl.glLineWidth(2); // Толщина линии
Gl.glBegin(Gl.GL_LINES); // Вывод линий, аппроксимирующих сплайн
for (int i = 0; i < m - 3; i++)
{
t = i;
while (t <= i + 1)
{
Gl.glVertex2d(xy(i, t, 0), xy(i, t, 1));
t += dt;
Gl.glVertex2d(xy(i, t, 0), xy(i, t, 1));
}
}
Gl.glEnd(); // Заканчиваем вывод линий
Gl.glFlush(); // Отображаем примитивы
CG2.Invalidate();
}
// Возвращает текущую x- или y-координату сплайна
private double xy(int i, double t, int j)
{
double t0 = t - i;
double t02 = t0 * t0;
double t03 = t02 * t0;
double t1 = 1.0 - t0;
double t12 = t1 * t1;
double t13 = t12 * t1;
return (t13 * V[i, j] + (3 * t03 - 6 * t02 + 4) * V[1 + i, j] + (-3 * t03 + 3 * t02 + 3 * t0 + 1) * V[2 + i, j] + t03 * V[3 + i, j]) / 6.0;
}
}
}
Порождается набором 16 точек Vij; i = 0, 1, 2, 3; j = 0, 1, 2, 3. Описывается следующим векторным параметрическим уравнением:
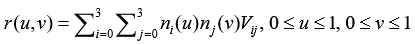
Функциональные коэффициенты n0, n1, n2, n3 те же, что и для кубической B-сплайновой кривой.
В матричной форме уравнение записывается следующим образом:
где
M - базисная матрица кубического B-сплайна;
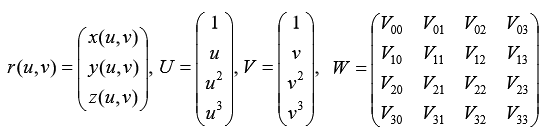
Элементарная бикубическая B-сплайновая поверхность:
Ниже приводится C#-программа, обеспечивающая построение составной бикубической B-сплайновой поверхности (рис. 4.5) на прямоугольной сетке [0, mx]×[0, my] (рис. 4.6) с равномерными узлами (i, j), i = 0, 1,..., mx, j = 0, 1,..., my.
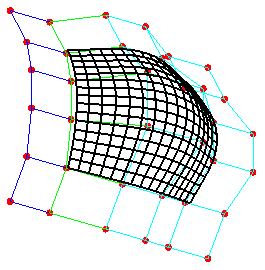
Рис. 4.5. 6×6-составная бикубическая B-сплайновая поверхность
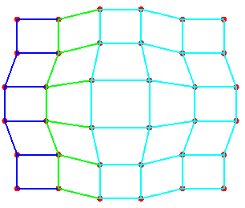
Рис. 4.6. 6×6-сетка задания составной бикубической B-сплайновой поверхности
using System;
using System.Windows.Forms;
// Для работы с библиотекой OpenGL
using Tao.OpenGl;
// Для работы с элементом управления SimpleOpenGLControl
using Tao.Platform.Windows;
namespace WindowsFormsApplication2
{
public partial class Form1 : Form
{
// Массив контрольных вершин для поверхности
double [,,] W = {
{{-25, -25, 5}, {-25, -15, 10}, {-28, -5, 15}, {-28, 5, 15}, {-25, 15, 10}, {-25, 25, 5}},
{{-15, -25, 5}, {-15, -15, 10}, {-18, -5, 15}, {-18, 5, 15}, {-15, 15, 10}, {-15, 25, 5}},
{{-5, -28, 10}, {-5, -18, 15}, {-7, -7, 25}, {-7, 7, 25}, {-5, 18, 15}, {-5, 28, 10}},
{{5, -28, 10}, {5, -18, 15}, {7, -7, 25}, {7, 7, 25}, {5, 18, 15}, {5, 28, 10}},
{{15, -25, 5}, {15, -15, 10}, {18, -5, 15}, {18, 5, 15}, {15, 15, 10}, {15, 25, 5}},
{{25, -25, 5}, {25, -15, 10}, {28, -5, 15}, {28, 5, 15}, {25, 15, 10}, {25, 25, 5}}};
int mx = 6, my = 6;
double ax = -25, ay = 40;
public Form1()
{
InitializeComponent();
CG2.InitializeContexts(); // CG2 - имя окна OpenGL
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
}
private void button1_Click(object sender, EventArgs e)
{
drawSurf();
}
private void drawSurf()
{
double dt = 0.2;
double u = 0, v = 0;
int i, j;
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
Gl.glMatrixMode(Gl.GL_PROJECTION); // Текущей стала матрица проецирования
Gl.glLoadIdentity();
Gl.glOrtho(-40, 40, -40, 40, -40, 40); // Матрица ортографического проецирования
Gl.glRotated(ax, 1.0, 0.0, 0.0); // Поворот вокруг оси Х на угол ax против часовой стрелки
Gl.glRotated(ay, 0.0, 1.0, 0.0); // Поворот вокруг оси Y на угол ay против часовой стрелки
Gl.glEnable(Gl.GL_POINT_SMOOTH); // Сглаживание точек
Gl.glPointSize(6); // Размер точки
Gl.glColor3d(1.0, 0.0, 0.0); // Текущий цвет красный
Gl.glBegin(Gl.GL_POINTS);
// Вывод контрольных вершин; m - число контрольных вершин
for (i = 0; i < mx; i++)
{
for (j = 0; j < my; j++)
{
Gl.glVertex3d(W[i, j, 0], W[i, j, 1], W[i, j, 2]);
}
}
Gl.glEnd(); // Заканчиваем вывод точек (контрольных вершин)
Gl.glColor3d(0.0, 0.0, 1.0); // Текущий цвет синий
Gl.glLineWidth(1); // Толщина линии
Gl.glPolygonMode(Gl.GL_FRONT_AND_BACK, Gl.GL_LINE);
Gl.glBegin(Gl.GL_QUADS); // Вывод полигонов по контрольным вершинам
for (i = 0; i < mx - 1; i++)
{
for (j = 0; j < my - 1; j++)
{
Gl.glVertex3d(W[i, j, 0], W[i, j, 1], W[i, j, 2]);
Gl.glVertex3d(W[i + 1, j, 0], W[i + 1, j, 1], W[i + 1, j, 2]);
Gl.glVertex3d(W[i + 1, j + 1, 0], W[i + 1, j + 1, 1], W[i + 1, j + 1, 2]);
Gl.glVertex3d(W[i, j + 1, 0], W[i, j + 1, 1], W[i, j + 1, 2]);
}
if (i == 0)
Gl.glColor3d(0.0, 1.0, 0.0); // Текущий цвет зеленый
else
Gl.glColor3d(0.0, 1.0, 1.0);
}
Gl.glEnd(); // Заканчиваем вывод
Gl.glLineWidth(2); // Толщина линии
Gl.glColor3d(0.0, 0.0, 0.0); // Текущий цвет черный
Gl.glBegin(Gl.GL_QUADS); // Вывод полигонов, аппроксимирующих сплайновую поверхность
for (i = 0; i < mx - 3; i++)
{
for (j = 0; j < my - 3; j++)
{
u = i;
while (u <= i+ 1)
{
v = j;
while (v <= j + 1)
{
Gl.glVertex3d(xyz(i, j, u, v, 0), xyz(i, j, u, v, 1), xyz(i, j, u, v, 2));
Gl.glVertex3d(xyz(i, j, u + dt, v, 0), xyz(i, j, u + dt, v, 1), xyz(i, j, u + dt, v, 2));
Gl.glVertex3d(xyz(i, j, u + dt, v + dt, 0), xyz(i, j, u + dt, v + dt, 1), xyz(i, j, u + dt, v + dt, 2));
Gl.glVertex3d(xyz(i, j, u, v + dt, 0), xyz(i, j, u, v + dt, 1), xyz(i, j, u, v + dt, 2));
v += dt;
}
u += dt;
}
}
}
Gl.glEnd(); // Заканчиваем вывод
Gl.glFlush(); // Отображаем примитивы на экране
CG2.Invalidate();
}
// Возвращает текущую x-, y- или z-координату сплайна
private double xyz(int i, int j, double u, double v, int k)
{
double u0 = u - i;
double u02 = u0 * u0;
double u03 = u02 * u0;
double u1 = 1.0 - u0;
double u12 = u1 * u1;
double u13 = u12 * u1;
double v0 = v - j;
double v02 = v0 * v0;
double v03 = v02 * v0;
double v1 = 1.0 - v0;
double v12 = v1 * v1;
double v13 = v12 * v1;
double [] SV = { 0, 0, 0, 0 };
for (int i2 = i; i2 < i + 4; i2++)
SV[i2 - i] = v13 * W[i2, j, k] + (3 * v03 - 6 * v02 + 4) * W[i2, j + 1, k] + (-3 * v03 + 3 * v02 + 3 * v0 + 1) * W[i2, j + 2, k] + v03 * W[i2, j + 3, k];
return (u13 * SV[0] + (3 * u03 - 6 * u02 + 4) * SV[1] + (-3 * u03 + 3 * u02 + 3 * u0 + 1) * SV[2] + u03 * SV[3]) / 36.0;
}
}
}
Назовем некоторые известные сплайн-функции одной переменной и сплайновые кривые:
Аналогичный список существует и для сплайн-функций двух переменных и сплайновых поверхностей.
Задания.
Написать программы, обеспечивающие построение:
Материалы употребляются для придания поверхности надлежащих цветовых характеристик. При работе с материалами в сцену следует ввести один или несколько источников света.
В общем случае задаются RGBA-значения диффузионного и зеркального отражения и фонового рассеивания и излучения материала (соответственно diffuse, specular, ambient и emission).
В OpenGL эти значения подаются glMaterial-процедуре.
Аналогичные компоненты имеет и источник света; для их задания в OpenGLупотребляется glLight-процедура.
В приводимом ниже примере применена только одна компонента цвета материала (диффузионная, GL_DIFFUSE) и источника света (рассеивание, GL_AMBIENT), для прочих компонент используются заданные по умолчанию значения.
В примере выводится один полигон, его вершины, нормали и точка в позиции источника света (рис. 5.1).
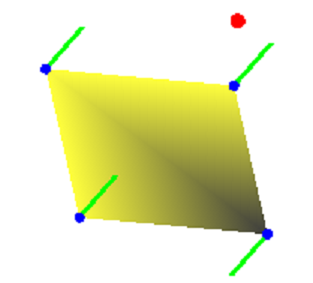
Рис. 5.1. Использован один источник света и диффузионная компонента материала
Полигон выводится с интерполяцией цветов. Нормали задаются к вершинам. Темный угол получен в результате соответствующего ориентирования нормали, заданной в вершине этого угла.
Рисунок получен средствами OpenGL после запуска следующей C#-программы:
using System;
using System.Windows.Forms;
// Для работы с библиотекой OpenGL
using Tao.OpenGl;
// Для работы с элементом управления SimpleOpenGLControl
using Tao.Platform.Windows;
namespace WindowsFormsApplication1
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
CG2.InitializeContexts(); // CG2 - имя окна OpenGL
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
}
private void button1_Click(object sender, EventArgs e)
{
float sx = 30, sy = 20;
double[,] P = { { sx, sy, 0 }, { sx + 30, sy, 0 }, { sx + 30, sy + 20, 0 }, { sx, sy + 20, 0 } };
double[,] N = { { 0, 0, -10 }, { 0, 0, 10 }, { 0, 0, -10 }, { 0, 0, -10 } };
float[] light_position = { sx + 10, sy + 10, -30, 0 }; // Координаты источника света
float[] lghtClr = { 1, 1, 1, 0 }; // Источник излучает белый цвет
float[] mtClr = { 1, 1, 0, 0 }; // Материал желтого цвета
int i = 0;
double ax2 = 35, ay2 = -30, az2 = 15;
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
Gl.glMatrixMode(Gl.GL_PROJECTION); // Текущей стала матрица проецирования
Gl.glLoadIdentity();
Gl.glOrtho(-10, 70, -10, 60, -60, 60); // Матрица ортографического проецирования
Gl.glRotated(ax2, 1.0, 0.0, 0.0); // Поворот вокруг оси Х на угол ax2 против часовой стрелки
Gl.glRotated(ay2, 0.0, 1.0, 0.0); // Поворот вокруг оси Y на угол ay2 против часовой стрелки
Gl.glRotated(az2, 0.0, 0.0, 1.0); // Поворот вокруг оси Z на угол az2 против часовой стрелки
Gl.glPolygonMode(Gl.GL_FRONT, Gl.GL_FILL); // Заливка полигонов
Gl.glShadeModel(Gl.GL_SMOOTH); // Вывод с интерполяцией цветов
Gl.glEnable(Gl.GL_LIGHTING); // Будем рассчитывать освещенность
Gl.glLightfv(Gl.GL_LIGHT0, Gl.GL_POSITION, light_position);
Gl.glLightfv(Gl.GL_LIGHT0, Gl.GL_AMBIENT, lghtClr);
Gl.glEnable(Gl.GL_LIGHT0); // Включаем в уравнение освещенности источник GL_LIGHT0
// Диффузионная компонента цвета материала
Gl.glMaterialfv(Gl.GL_FRONT, Gl.GL_DIFFUSE, mtClr);
Gl.glBegin(Gl.GL_QUADS); // Вывод полигона
for (i = 0; i < 4; i++)
{
Gl.glNormal3d(N[i, 0], N[i, 1], N[i, 2]);
Gl.glVertex3d(P[i, 0], P[i, 1], P[i, 2]);
}
Gl.glEnd(); // Заканчиваем вывод
Gl.glDisable(Gl.GL_LIGHTING); // Отменяем расчет освещенности
Gl.glColor3d(0.0, 1.0, 0.0); // Текущий цвет зеленый. Используется при выводе нормалей
Gl.glLineWidth(4); // Толщина линии
Gl.glBegin(Gl.GL_LINES); // Вывод нормалей
for (i = 0; i < 4; i++)
{
Gl.glVertex3d(P[i, 0], P[i, 1], P[i, 2]);
Gl.glVertex3d(P[i, 0] + N[i, 0], P[i, 1] + N[i, 1], P[i, 2] + N[i, 2]);
}
Gl.glEnd(); // Заканчиваем вывод
Gl.glColor3d(0.0, 0.0, 1.0); // Текущий цвет синий. Используется при выводе вершин
Gl.glPointSize(6); // Размер точки
Gl.glBegin(Gl.GL_POINTS);
// Вывод вершин
for (i = 0; i < 4; i++) Gl.glVertex3d(P[i, 0], P[i, 1], P[i, 2]);
Gl.glEnd(); // Заканчиваем вывод
Gl.glColor3d(1.0, 0.0, 0.0); // Текущий цвет красный. Используется при выводе точки в позиции источника света
Gl.glEnable(Gl.GL_POINT_SMOOTH); // Сглаживание точек
Gl.glPointSize(9); // Размер точки
Gl.glBegin(Gl.GL_POINTS);
Gl.glVertex3fv(light_position);
Gl.glEnd(); // Заканчиваем вывод
Gl.glFlush(); // Отображаем примитивы на экране
CG2.Invalidate();
}
}
}
В 3ds Max нормалями можно управлять средствами модификатора Edit Normals.
В случае, например, сферы (рис. 5.2) все полигоны входят в одну группу сглаживания, поэтому нормали рассчитываются к вершинам полигонов 3d-объекта; в случае прямоугольного параллелепипеда каждая его сторона входит в свою группу сглаживания, поэтому нормали рассчитываются к полигонам.
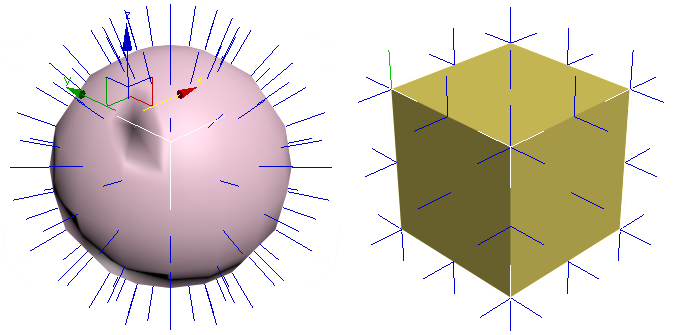
Рис. 5.2. Объекты с одной (сфера) и несколькими (куб) группами сглаживаниями
Темное пятно на поверхности сферы получено в результате изменения направления нормали к одной из вершин объекта.
Больше информации о материалах и можно получить, например, в работе Вывод граней OpenGL
Задание.
Написать два варианта программы, выводящей параболоид с использованием материалов. В первом варианте нормали рассчитывать к граням, во втором - к вершинам полигональной модели параболоида.
Текстура позволяет нанести на поверхность объекта подходящий рисунок (рис. 6.1).

Рис. 6.1. Число повторений текстуры по каждой координатной оси равно двум
Рисунок, использованный для получения текстуры, может быть загружен из файла.
Так же в качестве образа для текстуры можно употребить и созданный в программе массив.
В приводимом ниже коде текстура создается и по образу, хранимому в файле:
using System;
using System.Drawing; // Для Rectangle, Bitmap и RotateFlipType
using System.Windows.Forms;
// Для работы с библиотекой OpenGL
using Tao.OpenGl;
// Для работы с элементом управления SimpleOpenGLControl
using Tao.Platform.Windows;
namespace WindowsFormsApplication1
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
CG2.InitializeContexts(); // CG2 - имя окна OpenGL
Gl.glClearColor(1, 1, 1, 1);
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
}
private void Draw()
{
Gl.glClearColor(1.0f, 1.0f, 1.0f, 1.0f); // Белый фон
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
Gl.glMatrixMode(Gl.GL_PROJECTION); // Текущей стала матрица проецирования
Gl.glLoadIdentity();
Gl.glOrtho(-1.1, 1.1, -1.1, 1.1, -1.1, 1.1); // Матрица ортографического проецирования
Bitmap btmp = new Bitmap("C:\\mine\\CGBook\\cg1_6.png");
btmp.RotateFlip(RotateFlipType.Rotate180FlipX); // Вращаем и перевертываем образ
System.Drawing.Imaging.BitmapData data;
Rectangle Rect = new Rectangle(0, 0, btmp.Width, btmp.Height);
data = btmp.LockBits(Rect, System.Drawing.Imaging.ImageLockMode.ReadOnly,
System.Drawing.Imaging.PixelFormat.Format32bppRgb);
// Затираем существующее изображение
Gl.glTexEnvi(Gl.GL_TEXTURE_ENV, Gl.GL_TEXTURE_ENV_MODE, Gl.GL_DECAL);
//Gl.glTexParameterf(Gl.GL_TEXTURE_2D, Gl.GL_TEXTURE_WRAP_S, Gl.GL_REPEAT);
//Gl.glTexParameterf(Gl.GL_TEXTURE_2D, Gl.GL_TEXTURE_WRAP_T, Gl.GL_REPEAT);
Gl.glTexParameteri(Gl.GL_TEXTURE_2D, Gl.GL_TEXTURE_MIN_FILTER, Gl.GL_LINEAR);
Gl.glTexParameteri(Gl.GL_TEXTURE_2D, Gl.GL_TEXTURE_MAG_FILTER, Gl.GL_LINEAR);
Gl.glTexImage2D(Gl.GL_TEXTURE_2D, 0, 3, data.Width, data.Height,
0, Gl.GL_RGBA, Gl.GL_UNSIGNED_BYTE, data.Scan0);
btmp.UnlockBits(data);
Gl.glPolygonMode(Gl.GL_FRONT, Gl.GL_FILL); // Заливка полигонов
Gl.glColor3d(0.0, 0.0, 1.0); // Текущий цвет синий. Используется при выводе подложки
// Подложка
Gl.glDisable(Gl.GL_TEXTURE_2D);
Gl.glBegin(Gl.GL_QUADS);
Gl.glVertex2d(-0.85, -0.65); Gl.glVertex2d(0.85, -0.65);
Gl.glVertex2d(0.85, 0.65); Gl.glVertex2d(-0.85, 0.65);
Gl.glEnd();
// Полигон с текстурой. Повторяем образ дважды по каждой координатной оси
Gl.glEnable(Gl.GL_TEXTURE_2D);
Gl.glBegin(Gl.GL_QUADS);
Gl.glTexCoord2d(0, 0);
Gl.glVertex2d(-0.8, -0.6);
Gl.glTexCoord2d(2, 0);
Gl.glVertex2d(0.8, -0.6);
Gl.glTexCoord2d(2, 2);
Gl.glVertex2d(0.8, 0.6);
Gl.glTexCoord2d(0, 2);
Gl.glVertex2d(-0.8, 0.6);
Gl.glEnd();
Gl.glFlush(); // Отображаем примитивы на экране
CG2.Invalidate();
Gl.glDisable(Gl.GL_TEXTURE_2D);
}
private void buttonGo2_Click(object sender, EventArgs e)
{
Draw();
}
}
}
В случае OpenTK для вывода текстуры можно употребить следующий код:
Bitmap btmp = new Bitmap("G:\\AM\\Лекции\\but.png"); // Файл с четырьмя пуговицами
//
// Текстура из файла
btmp.RotateFlip(RotateFlipType.Rotate180FlipX); // Вращаем и перевертываем образ
System.Drawing.Imaging.BitmapData data;
Rectangle Rect = new Rectangle(0, 0, btmp.Width, btmp.Height);
data = btmp.LockBits(Rect, System.Drawing.Imaging.ImageLockMode.ReadOnly, System.Drawing.Imaging.PixelFormat.Format32bppRgb);
GL.Enable(EnableCap.Texture2D);
GL.TexEnv(TextureEnvTarget.TextureEnv, TextureEnvParameter.TextureEnvMode, (int)TextureEnvMode.Decal);
GL.TexParameter(TextureTarget.Texture2D, TextureParameterName.TextureMinFilter, (int)TextureMinFilter.Linear);
GL.TexImage2D(TextureTarget.Texture2D, 0, PixelInternalFormat.Rgb, width, height, 0, PixelFormat.Rgb, PixelType.UnsignedByte, image);
GL.TexImage2D(TextureTarget.Texture2D, 0, PixelInternalFormat.Rgba, data.Width, data.Height, 0, PixelFormat.Rgba, PixelType.UnsignedByte, data.Scan0);
btmp.UnlockBits(data);
GL.Enable(EnableCap.Texture2D);
GL.Begin(PrimitiveType.Polygon);
GL.TexCoord2(0, 0);
GL.Vertex2(-0.8f, -0.6f);
GL.TexCoord2(2, 0);
GL.Vertex2(0.8f, -0.6f);
GL.TexCoord2(2, 2);
GL.Vertex2(0.8f, 0.6f);
GL.TexCoord2(0, 2);
GL.Vertex2(-0.8f, 0.6f);
GL.End();
GL.Disable(EnableCap.Texture2D);
glControlWindow.SwapBuffers();
В качестве данных для тестуры можно употребить соответствующим образом заполненный трехмерный массив.
Объявим массив следующим образом:
public partial class Form1 : Form
{
int width = 64, height = 64; // Размеры текстуры
byte[, ,] image = new byte[64, 64, 3];
public Form1()
{
…
Так, текстуру Checker (рис. 6.2) можно создать по данным массива, заполняемого в следующим образом
private void makeImg()
{
// Генерация черно-белого образа, на основе которого создается текстура
for (int i = 0; i < width; i++)
for (int j = 0; j < height; j++)
{
byte bt = (byte)((i & 16 ^ j & 16) * 255); // 0 or 240
for (int k = 0; k < 3; k++) image[i, j, k] = bt;
}
}

Рис. 6.2. Текстура Checker из массива image
Разноцветная текстура Checker (рис. 6.3) генерируется по массиву из процедуры makeImgClr:
private void makeImgClr()
{
int i, j, k;
if (width != 64 || height != 64) { MessageBox.Show("Плохие размеры массива image"); return; }
// Генерация разноцветного образа, на основе которого создается текстура (width = height = 64)
// Инициализация образа белым цветом (255, 255, 255)
for (i = 0; i < 64; i++) for (j = 0; j < 64; j++) for (k = 0; k < 3; k++) image[i, j, k] = 255;
// Корректировка цвета образа
for (i = 16; i < 32; i++) for (j = 0; j < 16; j++) for (k = 0; k < 2; k++)
image[i, j, k] = 0; // 0, 0, 255
for (i = 48; i < 64; i++) for (j = 0; j < 16; j++) for (k = 1; k < 3; k++)
image[i, j, k] = 0; // 255, 0, 0
for (i = 0; i < 16; i++) for (j = 16; j < 32; j++)
image[i, j, 0] = 0; // 0, 255, 255
for (i = 31; i < 48; i++) for (j = 16; j < 32; j++)
image[i, j, 1] = 0; // 255, 0, 255
for (i = 16; i < 32; i++) for (j = 31; j < 48; j++)
image[i, j, 2] = 0; // 255, 255, 0
for (i = 48; i < 64; i++) for (j = 31; j < 48; j++)
{
image[i, j, 0] = 0; image[i, j, 2] = 0; // 0, 255, 0
}
for (i = 0; i < 16; i++) for (j = 48; j < 64; j++)
image[i, j, 0] = 100; // 100, 100, 255
for (i = 31; i < 48; i++) for (j = 48; j < 64; j++)
image[i, j, 1] = 100; // 255, 100, 100
}

Рис. 6.3. Разноцветная текстура Checker из массива image
Процедура, вызывающая makeImg или makeImgClr, формирующая текстуру и выводящая полигон с нанесенной текстурой:
private void DrawChecker(bool clr)
{
Gl.glClearColor(1, 1, 1, 1); // Белый фон
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT); // Очистка буфера цвета
Gl.glMatrixMode(Gl.GL_PROJECTION); // Текущей стала матрица проецирования
Gl.glLoadIdentity();
Gl.glOrtho(-1.1, 1.1, -1.1, 1.1, -1.1, 1.1); // Матрица ортографического проецирования
// Затираем существующее изображение
Gl.glTexEnvi(Gl.GL_TEXTURE_ENV, Gl.GL_TEXTURE_ENV_MODE, Gl.GL_DECAL);
Gl.glTexParameteri(Gl.GL_TEXTURE_2D, Gl.GL_TEXTURE_MIN_FILTER, Gl.GL_LINEAR);
Gl.glTexParameteri(Gl.GL_TEXTURE_2D, Gl.GL_TEXTURE_MAG_FILTER, Gl.GL_NEAREST);
// Создаем массив image с данными для текстуры
if (clr)
makeImgClr();
else
makeImg();
Gl.glTexImage2D(Gl.GL_TEXTURE_2D, 0, 3, width, height, 0, Gl.GL_RGB, Gl.GL_UNSIGNED_BYTE, image);
Gl.glPolygonMode(Gl.GL_FRONT, Gl.GL_FILL); // Заливка полигонов
Gl.glColor3d(0.0, 0.0, 1.0); // Текуший цвет синий. Используется при выводе подложки
// Подложка
Gl.glDisable(Gl.GL_TEXTURE_2D);
Gl.glBegin(Gl.GL_QUADS);
Gl.glVertex2d(-0.85, -0.65); Gl.glVertex2d(0.85, -0.65);
Gl.glVertex2d(0.85, 0.65); Gl.glVertex2d(-0.85, 0.65);
Gl.glEnd();
// Полигон с текстурой
Gl.glEnable(Gl.GL_TEXTURE_2D);
Gl.glBegin(Gl.GL_QUADS);
Gl.glTexCoord2d(0, 0);
Gl.glVertex2d(-0.8, -0.6);
Gl.glTexCoord2d(1, 0);
Gl.glVertex2d(0.8, -0.6);
Gl.glTexCoord2d(1, 1);
Gl.glVertex2d(0.8, 0.6);
Gl.glTexCoord2d(0, 1);
Gl.glVertex2d(-0.8, 0.6);
Gl.glEnd();
Gl.glFlush(); // Отображаем примитивы на экране
CG2.Invalidate();
Gl.glDisable(Gl.GL_TEXTURE_2D);
}
// Click-обработчики кнопок Go3 и Go4
private void Go3_Click(object sender, EventArgs e)
{
DrawChecker(false);
}
private void Go4_Click(object sender, EventArgs e)
{
DrawChecker(true);
}
В случае OpenTK для вывода текстуры можно употребить следующий код:
// Текстура из массива imageВ общем случае на поверхность объекта можно нанести несколько текстур (рис. 6.2).

Рис. 6.2. На поверхности куба заданы 3 текстуры
В частности, в 3ds Max это обеспечивается за счет назначения полигонам целочисленного свойства ID материала (MaterialIndex) и последующего употребления материала Multi/Sub Object (конструктор Multimaterial()).
Употребляемые при работе с текстурой преобразования и модели описаны частично, например, в работе Реализация схемы наложения текстуры
Задание.
Создать средствами C# и OpenGL полигональную модель из разноцветных граней одной из указанных ниже геометрических фигур (студентом выбирается фигура по его номеру в журнале группы).
Повернуть объект вокруг осей Y и X соответственно на 45° и 30°.
Организовать перемещение объекта по наклонной прямой с одновременным вращением вокруг оси Y.
Список геометрических фигур:
Назовем некоторые алгоритмы, употребляемые для удаления невидимых линий и поверхностей.
Описание и реализацию метода z-буфера можно найти, например, в работе Реализация метода Z-буфера удаления невидимых частей поверхности.
Задание.
Написать программу, реализующую метод плавающего горизонта.
Приведены сведения, которые передаются студентам 3-го курса по дисциплине компьютерной графики. Продолжительность учебного курса 1 семестр.
Факультативно студенты осваивают другие разделы компьютерной графики, в частности, следующие:
Кроме того, по курсу компьютерной графики доступны методические материалы.