Приводится MAXScript-реализация лучевого алгоритма, который, как и волновой алгоритм, употребляется для поиска пути между двумя ячейками – источником и приемником (рис. 1) дискретного рабочего поля (ДРП).
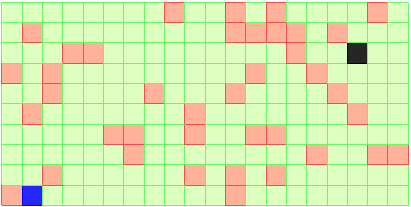
Рис. 1. ДРП: источник, приемник и препятствия
ДРП – это прямоугольник, разбитый на квадратные ячейки одинакового размера. Ячейки ДРП подразделяются на свободные, препятствия, источники и приемники. На рис. 1 свободные ячейки имеют светло-зеленый цвет, а препятствия – светло-коричневый. Источник залит синим цветом, а приемник – черным.
Путь может быть проложен только по свободным ячейкам.
Заметим, что ячейки, занятые пролагаемым путем, также образуют препятствия.
Лучевой алгоритм находит, в частности, применение в САПР печатных плат и интегральных схем для оценки качества размещения. При трассировке предпочтительнее употребление волнового алгоритма, более затратного, но всегда, в отличие от лучевого алгоритма, находящего существующий путь.
Путь может быть двух видов: ортогональный и ортогонально-диагональный. Путь первого вида состоит из отрезков, параллельных сторонам ДРП. Путь второго вида может вдобавок содержать диагональные отрезки (угол между таким отрезком и стороной ДРП равен 45 или 135 градусов).
В первом случае каждая ячейка имеет 4 соседа, а во втором – 8 (рис. 2).
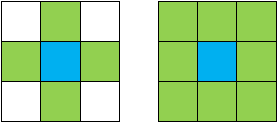
Рис. 2. Соседи ячейки в случае ортогонального и ортогонально-диагонального путей
Рассматривается алгоритм построения ортогонального пути. Алгоритм обеспечивает проведение ломаной линии, соединяющую источник и приемник и обходящую препятствия.
Искомый путь не должен пересекать сам себя.
Линия (луч) строится пошагово. На каждом шаге выполняется перемещение из текущей ячейки линии в свободную соседнюю ячейку, наиболее близкую к приемнику, что позволяет отнести лучевой алгоритм к разновидности жадного алгоритма.
Если достигнут приемник или все соседи текущей ячейки заняты, то процесс поиска пути прекращается.
Для определения расстояния между ячейками i и j используется ортогональная метрика:
dij = Δxij + Δyij,
где Δxij и Δyij – расстояния между ячейками i и j соответственно по осям X и Y. Единица измерения расстояния – ячейка.
Процесс распространения луча иллюстрирует рис. 3.
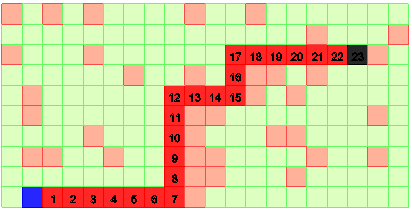
Рис. 3. Путь найден
На рис. 4 показана тупиковая ситуация.
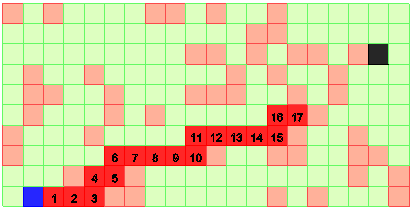
Рис. 4. Тупик: путь не найден
В алгоритме при поиске свободного соседа в первую очередь проверяется правый сосед, затем – верхний, затем – левый и в последнюю очередь – нижний.
Путь, находимый лучевым алгоритмом, не всегда является кратчайшим, что видно, например, из рис. 5.
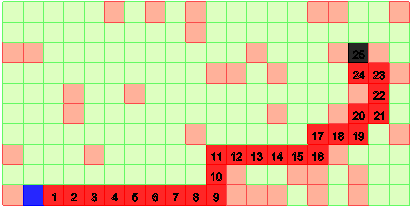
Рис. 5. Есть путь короче найденного
Приводимый ниже код обеспечивает следующие действия:
-- Возвращает true, если найдена свободная соседняя ячейка
fn fndCll kP2 arrB clrE clr i nT = (
if kP2 > 0 and kP2 <= nT do (
wc = arrB[kP2].WireColor
return wc == clrE or wc == clr
)
return false
)
-- Выбирает ячейку-источник или ячейку-приемник
fn ptPnt nx ny arrB clr2 clrPnt nP &x &y= (
local nSY, dn
dn = false
nSY = if nP == 1 then 1 else (ny - 1)
dx = 3
for k = nSY to nSY + 2 do (
k3 = (k - 1) * nx + (if nP == 1 then 1 else -dx)
y = if nP == 1 then k else k - 1
for k2 = 1 to dx do (
k4 = k3 + k2
if arrB[k4].WireColor != clr2 do (
dn = true
arrB[k4].WireColor = clrPnt
x = if nP == 1 then k2 + 1 else nx - dx + k2
return k4
)
)
)
)
delete $*
clr = color 100 250 100
clr2 = color 250 75 75
sz = 10
arrB = #()
nx = 20
ny = 10
nT = nx * ny
-- Формируем дискретное рабочее поле из nx* ny ячеек
arrB = for k = 1 to nT collect box length:sz width:sz height:1 lengthsegs:1 widthsegs:1 heightsegs:1 wireColor:clr
y = -0.5 * ny * sz
k3 = 0
for k = 1 to ny do (
y += sz
x = -0.5 * (nx - 3) * sz
for k2 = 1 to nx do (
k3 += 1
x += sz
arrB[k3].Pos = [x, y , 0]
)
)
nC = 0.2 * nT
-- Формируем nC ячеек-препятствий
for k = 1 to nC do (
k2 = random 1 nT
arrB[k2].WireColor = clr2
)
xS = yS = xE = yE = 0
-- Выбираем ячейку-источник
kS = ptPnt nx ny arrB clr2 blue 1 &xS &yS
-- Выбираем ячейку-приемник
kE = ptPnt nx ny arrB clr2 black 2 &xE &yE
-- Формирование пути
kC = kS
nMx = 100
i = 0
kT = 0.6
x = xS
y = yS
d = abs (xE - x) + abs (yE - y)
while i < nMx and kC != kE do (
arrD = #(d, d, d, d)
i += 1
-- Находим свободного, ближайшего к приемнику соседа текущей ячейки kC
if mod kC nx != 0 and fndCll (kC + 1) arrB black clr i nT do arrD[1] = abs (xE - x - 1) + abs (yE - y)
if fndCll (kC + nx) arrB black clr i nT do arrD[2] = abs (xE - x) + abs (yE - y - 1)
if mod kC nx != 1 and fndCll (kC - 1) arrB black clr i nT do arrD[3] = abs (xE - x + 1) + abs (yE - y)
if fndCll (kC - nx) arrB black clr i nT do arrD[4] = abs (xE - x) + abs (yE - y + 1)
dM = amin arrD
if dM == d do (
messageBox("The path is not found")
exit
)
kM = findItem arrD dM
case kM of (
1: (x += 1; kC += 1)
2: (y += 1; kC += nx)
3: (x -= 1; kC -= 1)
4: (y -= 1; kC -= nx)
)
bx = arrB[kC]
bx.WireColor = red
text text:(i as string) size:(kT * sz) pos:(bx.pos + [0, -0.5 * kT * sz, 1.01 * bx.height]) wireColor:black
if kC == kE do bx.WireColor = black
)
Лучевой алгоритм имеет линейную вычислительную сложность. Однако низкая эффективность алгоритма существенно сужает область его применения.