Приводится MAXScript-реализация волнового алгоритма, употребляемого для поиска пути между двумя ячейками – источником и приемником (рис. 1) дискретного рабочего поля (ДРП).

Рис. 1. ДРП: источник, приемник и препятствия
ДРП – это прямоугольник, разбитый на квадратные ячейки одинакового размера. Ячейки ДРП подразделяются на свободные, препятствия, источники и приемники. На рис. 1 свободные ячейки имеют светло-зеленый цвет, а препятствия – светло-коричневый. Источник залит синим цветом, а приемник – черным.
Путь может быть проложен только по свободным ячейкам.
Волновой алгоритм находит, в частности, применение в САПР печатных плат и интегральных схем при решении задачи трассировки. Иная сфера применения волнового алгоритма – это игровые приложения.
Путь может быть двух видов: ортогональный и ортогонально-диагональный. Путь первого вида состоит из отрезков, параллельных сторонам ДРП. Путь второго вида может вдобавок содержать диагональные отрезки (угол между таким отрезком и стороной ДРП равен 45 или 135 градусов).
В первом случае каждая ячейка имеет 4 соседа, а во втором – 8 (рис. 2).
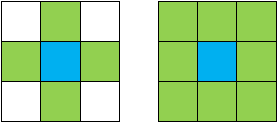
Рис. 2. Соседи ячейки в случае ортогонального и ортогонально-диагонального путей
Рассматривается алгоритм построения ортогонального пути. Алгоритм состоит из двух частей. В первой от источника к приемнику распространяется волна. Во второй выполняется обратный ход, в процессе которого из ячеек волны формируется путь.
Волна, идущая от источника к приемнику, на каждом шаге первой части алгоритма пополняется свободными ячейками ДРП, которые, во-первых, еще не принадлежат волне, и, во-вторых, являются 4-соседями ячеек, попавших в волну на предыдущем шаге.
Процесс распространения волны иллюстрируют рис. 3 – 6.
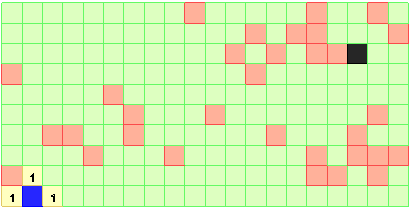
Рис. 3. Первый шаг распространения волны
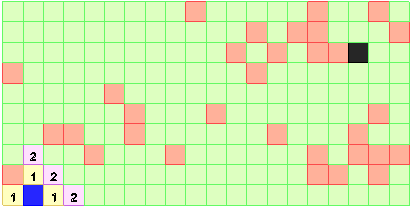
Рис. 4. Второй шаг распространения волны
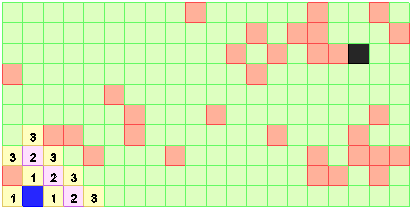
Рис. 5. Третий шаг распространения волны
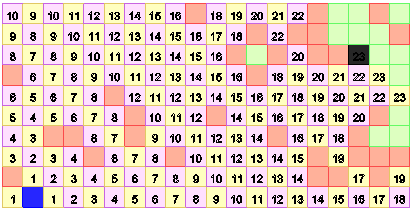
Рис. 6. Последний шаг распространения волны
В примере волна достигла ячейку-приемник за 23 шага.
При обратном ходе в путь включается по одной ячейке каждого шага распространения волны. При выборе из двух ячеек приоритет имеет ячейка, обеспечивающая горизонтальное продвижение, что приводит к пути, показанному на рис. 7.
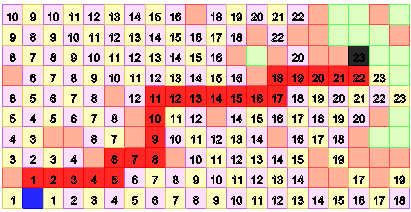
Рис. 7. Обратный ход: формирование пути
Волновой алгоритм либо находит кратчайший путь от источника к приемнику, либо информирует о неудаче, если путь к приемнику блокируется препятствиями.
Реализация волнового алгоритма выполнена в интересах учебного процесса.
Приводимый ниже код обеспечивает следующие действия:
-- Возвращает true, если найдена очередная ячейка пути, и добавляет эту ячейку в массив arrP
fn chkBx kP2 arrB clr3 clr4 nT arrT arrP &kP = (
if kP2 > 0 and kP2 <= nT do (
wc = arrB[kP2].WireColor
if wc == clr3 or wc == clr4 do (
t = (arrT[kP].Text as integer) - 1
t2 = arrT[kP2].Text as integer
if t == t2 do (
append arrP kP2
kP = kP2
return true
)
)
)
return false
)
-- Добавляет в массив arrF2 номер ячейки формируемой волны и меняет цвет этой ячейки
fn ppdTRrF2 arrB clr clr2 clr3 nT mC sz i arrF2 arrT = (
local bx, wc, kT = 0.6
if mC > 0 and mC <= nT do (
bx = arrB[mC]
wc = bx.WireColor
if wc == clr or wc == clr2 do (
appendIfUnique arrF2 mC
bx.WireColor = clr3
arrT[mC] = text text:(i as string) size:(kT * sz) pos:(bx.pos + [0, -0.5 * kT * sz, 1.01 * bx.height]) wireColor:black
)
)
)
-- Выбирает ячейку-источник или ячейку-приемник
fn ptPnt nx ny arrB clr2 clrPnt nP = (
local nSY, dn
dn = false
nSY = if nP == 1 then 1 else (ny - 1)
for k = nSY to nSY + 2 do (
k3 = (k - 1) * nx + (if nP == 1 then 1 else -3)
for k2 = 1 to 3 do (
k4 = k3 + k2
if arrB[k4].WireColor != clr2 do (
dn = true
arrB[k4].WireColor = clrPnt
return k4
)
)
)
)
delete $*
clr = color 100 250 100
clr2 = color 250 75 75
clr3 = color 225 200 100
clr4 = color 200 100 225
sz = 10
arrB = #()
nx = 20
ny = 10
nT = nx * ny
-- Формируем дискретное рабочее поле из nx* ny ячеек
arrB = for k = 1 to nT collect box length:sz width:sz height:1 lengthsegs:1 widthsegs:1 heightsegs:1 wireColor:clr
y = -0.5 * ny * sz
k3 = 0
for k = 1 to ny do (
y += sz
x = -0.5 * (nx - 3) * sz
for k2 = 1 to nx do (
k3 += 1
x += sz
arrB[k3].Pos = [x, y , 0]
)
)
nC = 0.2 * nT
-- Формируем nC ячеек-препятствий
for k = 1 to nC do (
k2 = random 1 nT
arrB[k2].WireColor = clr2
)
-- Выбираем ячейку-источник
kS = ptPnt nx ny arrB clr2 blue 1
-- Выбираем ячейку-приемник
kE = ptPnt nx ny arrB clr2 black 2
-- Формируем волну от источника к приемнику, закрашивая добавляемые ячейки поочередно в цвета clr3 и clr4
arrF = #(kS)
arrF2 = #()
arrT = for k = 1 to nT collect k
i = 0
clr5 = clr3
nMx = 100
fnd = false
while i < nMx do (
i += 1
clr5 = if mod i 2 == 1 then clr3 else clr4
for k = 1 to arrF.Count do (
m = arrF[k]
if mod m nx != 1 do ppdTRrF2 arrB clr black clr5 nT (m - 1) sz i arrF2 arrT
ppdTRrF2 arrB clr black clr5 nT (m - nx) sz i arrF2 arrT
if mod m nx != 0 do ppdTRrF2 arrB clr black clr5 nT (m + 1) sz i arrF2 arrT
ppdTRrF2 arrB clr black clr5 nT (m + nx) sz i arrF2 arrT
)
arrF = deepCopy arrF2
-- fnd = true, если волна достигла ячейку-приемник
fnd = findItem arrF2 kE > 0
if fnd do (
arrB[kE].WireColor = black
exit
)
arrF2 = #()
)
if fnd then (
-- Обратный ход от приемника к источнику
-- Формируем массив arrP, содержащий номера ячеек, принадлежащих искомому пути
arrP = #()
kP = kE
i = 0
while i < nMx do (
i += 1
if mod kP nx != 1 do if chkBx (kP - 1) arrB clr3 clr4 nT arrT arrP &kP do continue
if chkBx (kP - nx) arrB clr3 clr4 nT arrT arrP &kP do continue
if mod kP nx != 0 do if chkBx (kP + 1) arrB clr3 clr4 nT arrT arrP &kP do continue
if chkBx (kP + nx) arrB clr3 clr4 nT arrT arrP &kP do continue
)
-- Закрашиваем ячейки найденного пути красным цветом
for k = 1 to arrP.Count do (
k2 = arrP[k]
arrB[k2].wireColor = red
)
)
else messageBox("The path is not found")
Вычислительная сложность волнового алгоритма близка к O(N2). В реальных задачах, например при трассировке печатных плат, проложение пути (трассы) выполняется многократно, что влечет существенные временные затраты. Гораздо быстрее работает лучевой алгоритм, однако его применение ограничено низкой результативностью.