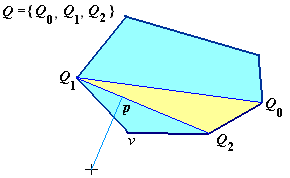
Рис. 5. Третий шаг алгоритма GJK
В ряде компьютерных приложений возникает задача обнаружения столкновения тел с целью его последующей обработки, которая зависит от вида тел (твердые, мягкие и др.).
Один из способов решения этой задачи состоит в постоянном контроле расстояния между парой перемещающихся тел. Нулевое расстояние означает, что тела соприкасаются.
Поскольку контроль расстояния осуществляется с некоторым временным шагом, то вместо соприкосновения пары тел может возникнуть их взаимное проникновение. В этом случае возникает задача устранения проникновения или иной реакции на это событие.
В работе рассматривается алгоритм Гилберта-Джонсона-Кёрти (Gilbert-Johnson-Keerthi algorithm, GJK), определяющий расстояние между двумя выпуклыми множествами, либо фиксирующий их взаимное проникновение.
Такими множествами могут быть, в частности, полигональные модели выпуклых 3-d объектов или выпуклые многоугольники.
В случае невыпуклого объекта либо строится его выпуклая оболочка, которая затем используется в задаче анализа столкновений, либо невыпуклое тело разбивается на выпуклые фрагменты.
В работе приводится программная реализация алгоритма GJK для 2-d случая, то есть алгоритм оперирует выпуклыми многоугольниками. Язык программирования MAXScript.
Алгоритм реализован в интересах учебного процесса.
Алгоритма GJK в своей работе использует в том числе следующие понятия:
Суммой Минковского двух подмножеств A и B линейного пространства V называется множество, состоящее из сумм всевозможных векторов из A и B:
A + B = {a + b: a ∈ a, b ∈ B}
Если A и B – это полигональные модели 3d-объектов или многоугольники (рис. 1), то a и b – это вершины геометрических фигур.
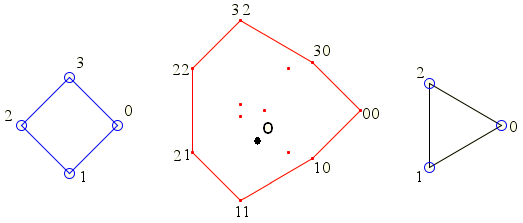
Рис. 1. Сумма Минковского четырехугольника и треугольника. О – начало координат
Выпуклая оболочка суммы Минковского показана на рис. 1 красным цветом. Вершины, эту оболочку образующие, пронумерованы. Вершины, находящиеся внутри оболочки, принадлежащие сумме Минковского, выведены без номеров.
В задаче анализа столкновений используется сумма Минковского, в которой координаты вершин многоугольника B берутся с обратным знаком, то есть анализируется фигура A – B.
Конфигурационное пространство препятствий (Configuration Space Obstacle, CSO) выпуклых объектов A и B – это A – B (рис. 2).
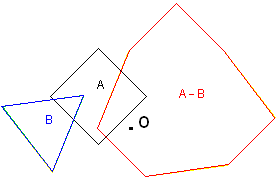
Рис. 2. Конфигурационное пространство препятствий
Известно, что A и B пересекаются, когда их CSO содержит начало координат.
Зная CSO, можно вычислить либо расстояние между телами, если они не пересекаются, либо глубину их взаимного проникновения.
Расстояние (Distance, d) и глубина проникновения (Penetration Depth, p) тел А и В – это минимальное расстояние, на которое нужно переместить одно тело, чтобы оно стало касаться другого тела. Вдобавок при поиске d или p определяется и направление перемещения.
Расстояние между A и B: d(A, B) = min{||x||: x ∈ CSO}
Глубина проникновения A и B: p(A, B) = inf{||x||: x ∈ CSO}
То есть вычисление d(A, B) или p(A, B) эквивалентно определению точки x, принадлежащей CSO, наиболее близкой к началу координат.
Для соприкосновения тел достаточно переместить тело B на расстояние d(A, B), если тела не пересекаются, или на расстояние p(A, B) – в противном случае. В первом случае перемещение выполняется в направлении вектора от найденной точки x до начала координат, во втором – направление перемещения меняет знак.
В случае касающихся тел d(A, B) = p(A, B) = 0.
Опорная функция (Support Mapping) SС(p) – это функция, которая принимает вектор p и выпуклое тело С и возвращает экстремальную точку выпуклого объекта С в направлении вектора p (рис. 3).
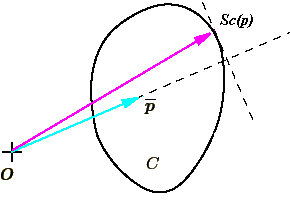
Рис. 3. Вычисление опорной функции
Поиск экстремальной точки выполняется по следующему критерию: скалярное произведение вектора p и вектора, проведенного из начала координат к экстремальной точке, превышает аналогичное значение для любой иной точки выпуклого объекта C.
В частности, для окружности экстремальная точка в направлении вектора p – это точка окружности, полученная при проведении радиуса окружности, параллельного p (рис. 4).
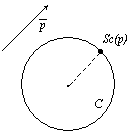
Рис. 4. Экстремальная точка окружности в направлении p
Известно, что SA – B(p) = SA(p) – SB(-p)
Плоскость H(p, δ) разделяет A и B, если для каждой точки a ∈ A справедливо (p, a) + δ ≥ 0, и для каждой точки b ∈ B справедливо (p, b) + δ ≥ 0.
Вектор p называют слабо отделённой осью (weakly separating axis), если для A и B имеется по крайней мере одна разделяющая плоскость (Separating Plane/Axis), нормалью к которой этот вектор является. Формально: (p, SA (-p)) ≥ (p, SB(p)).
В алгоритме GJK в случае полигональных моделей или многоугольников симплекс – это фигура, образованная подмножеством одной, двух, трех или четырех вершин CSO. То есть симплекс алгоритма GJK это либо точка, либо отрезок, либо треугольник, либо тетраэдр (последний случай возникает при работе с 3d-объектами).
Алгоритм GJK изучает CSO объектов A и B в поисках симплекса, который содержит начало координат.
Если такого симплекса нет, то есть начало системы координат лежит вне CSO, то A и B не пересекаются. В этом случае точка CSO, ближайшая к началу координат, представляет разделяющую плоскость A и B.
Если A и B пересекаются, то точка CSO, ближайшая к началу координат, представляет глубину проникновения A и B. Заметим, что такая точка в приводимом алгоритме не ищется, а лишь фиксируется факт взаимного проникновения фигур.
Алгоритм GJK не требует определения суммы Минковского С = A – B, а на каждой итерации находит экстремальную вершину CSO, добавляемую, если решение не найдено, в новую версию симплекса и приближающую текущую версию симплекса к началу координат (перед добавлением в симплекс найденной экстремальной вершины из него удаляется одна или две "бесперспективные" вершины).
Пересечение фигур, если таковое наблюдается, в приводимом ниже алгоритме фиксируется в результате обнаружения начала координат в пределах текущего симплекса (выводится сообщение Penetration).
Если пересечение не обнаружено, то после построения конечного симплекса проверяется факт наличия плоскости, разделяющей фигуры. Если такая плоскость имеется, то выводится расстояние между фигурами, в противном случае выводится сообщение Distance 0.
Схема алгоритма GJK:

Рис. 5. Третий шаг алгоритма GJK
При завершении вычислений по условию п. 6 прежде проверяется, есть ли плоскость, разделяющая изучаемые фигуры. Если такая плоскость имеется, то выводится расстояние между фигурами (длина вектора от начала координат к p), в противном печатается "Distance 0".
Для ликвидации пересечения в случае твердых тел определяется глубина проникновения. Решение этой задачи выходит за рамки настоящей работы.
Код, реализующий алгоритм GJK для двумерного случая, обеспечивает графическую иллюстрацию процесса поиска расстояния между фигурами (рис. 6).
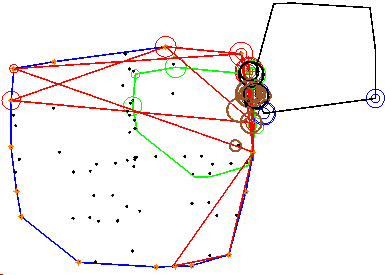
Рис. 6. Иллюстрация процесса вычисления расстояния между фигурами
На рис. 6 зеленым и черным цветом показаны изучаемые фигуры, красным - симплексы. Точки (вершины) фигуры A – B показаны черным цветом, а ее выпуклая оболочка - синим цветом. Начало координат отображается коричневой точкой.
На каждом шаге в экстремальных вершинах фигур и экстремальной вершине их разности выводятся окружности. При этом на каждом шаге радиус выводимой окружности увеличивается на две единицы. Также на каждом шаге рисуется коричневая окружность в точке, определяющей вектор, в направлении которого вычисляются экстремальные вершины фигур. На заключительном шаге, если проникновение фигур не обнаружено, выводятся черные окружности в вершине последнего симплекса, наиболее близкой к началу координат и в соответствующих вершинах исходных фигур.
Множество вершин A – B и их выпуклая оболочка формируются для иллюстративных целей и алгоритмом не используются.
При частичном запрете графического вывода (prn = false) работу программы будет сопровождать не столь насыщенный рисунок (рис. 7).
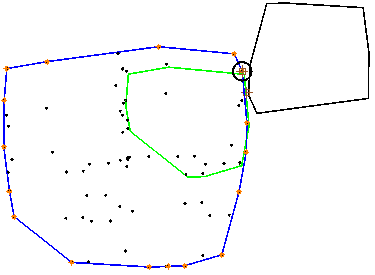
Рис. 7. Наложен частичный запрет на графический вывод
Помимо исходных фигур, CSO и выпуклой оболочки CSO, на рис. 7 видны начало координат, вершина CSO, ближайшая к началу координат, и черная окружность с центром в этой вершине.
Случай обнаруженного пересечения фигур показан на рис. 8.
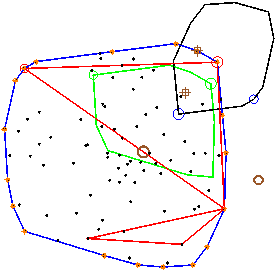
Рис. 8. Обнаружено взаимное проникновение многоугольников
Последний рисунок показывает, что симплекс, в пределах которого обнаружено начало координат, не может быть использован для расчета глубины проникновения (есть симплексы, дающие меньшие оценки этой величины).
Приведенные результаты, полученные на основе алгоритма GJK, обеспечивает следующий код:
-- Функция sLft получает точки v0, v1 и v2 и возвращает
-- положительное число, если v2 находится слева от линии, проведенной через v0 и v1
-- 0, если v2 – на линии
-- отрицательное число, если v2 находится справа от линии
fn sLft v0 v1 v2 = (v1[1] - v0[1]) * (v2[2] - v0[2]) - (v2[1] - v0[1]) * (v1[2] - v0[2])
-- Функция clcCf возвращает массив коэффициентов прямой, проходящей через точки v и v2
-- Используем каноническое уравнение прямой Ax + By + C = 0
fn clcCf v vv = (
local x1, y1, x2, y2, dx, dy, A, B, C
x1 = v[1]
y1 = v[2]
x2 = vv[1]
y2 = vv[2]
dx = x2 - x1
dy = y2 - y1
case of (
(dx == 0.0): (A = 1; B = 0; C = -x1)
(dy == 0.0): (A = 0; B = -1; C = y1)
default: (A = dy / dx; B = -1; C = -A * x1 + y1)
)
return #(A, B, C)
)
-- Функция clcCfNrml возвращает массив коэффициентов прямой, перпендикулярной прямой
-- с коэффициентами, хранимыми массивом arrCf
fn clcCfNrml arrCf = (
local A, B, C
A = arrCf[1]
B = arrCf[2]
C = arrCf[3]
return if B == 0 then #(0, 1.0, 0) else if A == 0 then #(1.0, 0, 0) else #(-1.0 / (A / B), 1.0, 0)
)
-- Функция pntrFnd вернет true, если начало координат находится внутри текущего симплекса
fn pntrFnd arrQ = (
if arrQ.Count == 3 then
return sLft arrQ[1] arrQ[2] [0, 0, 0] > 0 \
and sLft arrQ[2] arrQ[3] [0, 0, 0] > 0 \
and sLft arrQ[3] arrQ[1] [0, 0, 0] > 0
else
return false
)
-- Функция fndVN возвращает координаты точки пересечения прямых с коэффициентами,
-- хранимыми массивами arrCf и arrCf2
fn fndVN arrCf arrCf2 = (
local A, B, C, A2, B2, C2, x, y
A = arrCf[1]
B = arrCf[2]
C = arrCf[3]
case of (
-- Вторая прямая проходит через начало координат
-- Прямые перпендикулярны
(A == 0): return point3 0 (-C / B) 0
(B == 0): return point3 (-C / A) 0 0
default: (
A2 = arrCf2[1]
B2 = arrCf2[2]
C2 = arrCf2[3]
bb = B2 / B
x = C * bb / (A2 - A * bb) - C2
y = -(A * x + C) / B
return point3 x y 0
)
)
)
-- Находит экстремальную точку множества вершин arrNG в направлении vNCrnt
fn fndSCP arrNGC vNCrnt = (
local dtPrd, dtPrd2, cnt, k, kV
kV = 1
dtPrd = arrNGC[1][1] * vNCrnt[1] + arrNGC[1][2] * vNCrnt[2]
cnt = arrNGC.Count
for k = 2 to cnt do (
dtPrd2 = arrNGC[k][1] * vNCrnt[1] + arrNGC[k][2] * vNCrnt[2]
if dtPrd2 > dtPrd do (
kV = k
dtPrd = dtPrd2
)
)
return arrNGC[kV]
)
-- Находит на отрезке v vv точку, ближайшую к началу координат
-- Возвращает массив, содержащий найденную точку, вершины обновленного симплекса,
-- расстояние от начала координат до найденной точки,
-- удаляемые из симплекса (массива arrQ) вершины
-- координаты точки пересечения прямых с коэффициентами, хранимыми массивами arrCf и arrCfNrml
fn fndClsPnt v vv arrQ vDlt = (
local arrCf, arrCfNrml, vN, vNw, dMn, d1, d2
arrCf = clcCf v vv
-- Массив коэффициентов прямой, перпендикулярной прямой с коэффициентами,
-- хранимыми массивом arrCf
arrCfNrml = clcCfNrml arrCf
-- Находим координаты точки пересечения прямых с коэффициентами,
-- записанными в массивы arrCf и arrCfNrml
vN = fndVN arrCf arrCfNrml
dMn = sqrt (vN[1] * vN[1] + vN[2] * vN[2])
-- Если точка vN лежит между v и vv, то оставим в симплексе две вершины
-- В противном случае оставим в симплексе одну ближайшую к началу координат вершину
d1 = v[1] * v[1] + v[2] * v[2]
d2 = vv[1] * vv[1] + vv[2] * vv[2]
dMn12 = amin d1 d2
if dMn12 == d1 then (
vNw = v
vDlt2 = arrQ[2]
)
else (
vNw = vv
vDlt2 = arrQ[1]
)
if vN[2] > v[2] and vN[2] < vv[2] then
return #(vNw, #(v, vv), dMn, #(vDlt), vN)
else
return #(vNw, #(vNw), dMn, #(vDlt, vDlt2), vN)
)
-- Функция fndDMn возвращает расстояние между многоугольниками,
-- Расстояние возвращается равным нулю, если между многоугольниками нет разделяющей плоскости
fn fndDMn arrQ arrQV vA vB prn = (
local sP, k, vAk, vBk, v, kMn, dMn, d, vNN
-- Находим вершину vMn конечного симплекса arrQ, наиболее близкую к началу координат,
-- а также вершины vAk и vBk исходных многоугольников, дающие вершину vMn,
-- и точку vNN на границе симплекса (или ее продолжении), наиболее близкую к началу координат
v = arrQ[1]
vMn = v
dMn = sqrt (v[1] * v[1] + v[2] * v[2])
for k = 2 to arrQ.Count do (
v = arrQ[k]
d = sqrt (v[1] * v[1] + v[2] * v[2])
if d < dMn do (
vMn = v
dMn = d
)
)
for k = 1 to arrQV.Count do (
vAk = arrQV[k][1]
vBk = arrQV[k][2]
vNN = arrQV[k][3]
if vAk - vBk == vMn do exit
)
-- Для отображения результата выводим следующие окружности:
-- в вершине vMn, ближайшей к началу координат (r = 15, цвет черный)
circle pos:vMn radius:15 wireColor:black render_renderable:on \
render_displayRenderMesh:on render_thickness:2.0
if prn do (
-- в вершинах исследуемых фигур, дающих вершину vMn (r = 20, цвет черный)
circle pos:vAk radius:20 wireColor:black render_renderable:on \
render_displayRenderMesh:on render_thickness:2.0
circle pos:vBk radius:20 wireColor:black render_renderable:on \
render_displayRenderMesh:on render_thickness:2.0
-- в точке пересечения границы симплекса, ближайшей к началу координат
-- с линией проходящей через начало кординат и перпендикулярной этой границе (r = 15, цвет коричневый)
circle pos:vNN radius:15 wireColor:brown render_renderable:on \
render_displayRenderMesh:on render_thickness:2.0
)
-- Проверяем наличие разделяющей плоскости между фигурами
sp = vMn[1] * vNN[1] + vMn[2] * vNN[2] >= 0
return if sP then (distance [0, 0, 0] vNN) else 0
)
-- Функция рисует фигуру по массиву точек arrNG
fn drwNG arrNG ps clr fCls fPts thck = (
local spln, nMN, dMn, dMnCrnt, k, v
spln = line pos:ps wireColor:clr \
render_renderable:on render_displayRenderMesh:on render_thickness:thck
addNewSpline spln
nMn = 1
dMn = arrNG[nMn][1] * arrNG[nMn][1] + arrNG[nMn][2] * arrNG[nMn][2]
for k = 1 to arrNG.Count do (
v = arrNG[k]
addKnot spln 1 #corner #line v
dMnCrnt = v[1] * v[1] + v[2] * v[2]
-- Находим вершину, ближайшую к началу координат
if dMnCrnt < dMn do (
nMn = k
dMn = dMnCrnt
)
if fPts do point pos:arrNG[k] size:10 drawOnTop:on box:on wireColor:orange
)
-- Выводим вершину выпуклого многоугольника, ближайшую к началу координат
if fPts do point pos:arrNG[nMn] size:20 drawOnTop:on box:on wireColor:brown
if fCls do close spln 1
updateShape spln
)
fn compareFN v1 v2 k:1 = (
local d = v1[k] - v2[k]
case of (
(d < 0.): -1
(d > 0.): 1
default: 0
)
)
-- Строит выпуклую оболочку точек, хранимых массивом arrMS2
fn cnvxHll arrMS2 = (
-- Сортируем точки по возрастанию их х-координаты
qsort arrMS2 compareFN k:1
-- Вывод ломаной линии
-- drwNG arrMS2 [0, 0, 0] (color 255 0 0) false true 1.0
-- Построение выпуклой оболочки
-- arrCnvxMS - массив вершин выпуклой оболочки
v1 = arrMS2[1]
v2 = arrMS2[2]
if arrMS2[1][2] < arrMS2[2][2] do (
v1 = v2
v2 = arrMS2[1]
)
cnt2 = arrMS2.Count
v3 = arrMS2[cnt2 - 1]
v4 = arrMS2[cnt2]
if arrMS2[cnt2 - 1][2] > arrMS2[cnt2][2] do (
v3 = v4
v4 = arrMS2[cnt2 - 1]
)
arrCnvxMS = #(v1, v2, v3, v4)
arrCtv = #(1, 4, 2, 3)
for k = 1 to 2 do deleteItem arrMS2 1
for k = 1 to 2 do deleteItem arrMS2 arrMS2.Count
--drwNG arrCnvxMS [0, 0, 0] (color 0 255 255) true true 1.0
-- Вывод вершин массива arrMS2
cnt2 = arrMS2.Count
-- for k = 1 to cnt2 do point pos:arrMS2[k] size:5 drawOnTop:on box:on wireColor:black
for k = 1 to cnt2 do (
v = arrMS2[k]
sd = sLft arrCnvxMS[arrCtv[1]] arrCnvxMS[arrCtv[2]] v
m = 0
if sd > 0 then
m = 1
else (
sd = sLft arrCnvxMS[arrCtv[3]] arrCnvxMS[arrCtv[4]] v
if sd < 0 do m = 4
)
if m > 0 do (
insertItem v arrCnvxMS arrCtv[m]
arrCtv[2] += 1
arrCtv[3] += 1
arrCtv[4] += 1
)
)
-- drwNG arrCnvxMS [0, 0, 0] (color 0 255 255) true true 1.0
-- Выправляем полученную оболочку
dltd = true
while dltd do (
dltd = false
k = 1
while k <= arrCnvxMS.Count do (
cnt = arrCnvxMS.Count
case k of (
cnt: (k2 = 2; k3 = 1)
(cnt - 1): (k2 = 1; k3 = cnt)
default: (k2 = k + 2; k3 = k + 1)
)
if sLft arrCnvxMS[k] arrCnvxMS[k2] arrCnvxMS[k3] > 0 then (
deleteItem arrCnvxMS k3
dltd = true
)
else
k += 1
)
)
return arrCnvxMS
)
delete $*
-- Если prn = true, то выполняется графическая иллюстрация работы программы
prn = true
-- Массивы с координатами тестовых множеств вершин
-- Координаты точек задаем, употребляя датчик случайных чисел
n = 25
dx = 0
xMn = -160.0 - dx
xMx = 50.0 - dx
yMn = -150.0
yMx = 50.0
arrNG0 = for k = 1 to n collect (point3 (random xMn xMx) (random yMn yMx) 0)
arrNG0_ = for k = 1 to arrNG0.Count collect arrNG0[k]
xMn2 = -40.0 + dx
xMx2 = 160.0 + dx
yMn2 = -50.0
yMx2 = 150.0
arrNG20 = for k = 1 to n collect (point3 (random xMn2 xMx2) (random yMn2 yMx2) 0)
arrNG20_ = for k = 1 to arrNG20.Count collect arrNG20[k]
arrNG = cnvxHll arrNG0_
arrNG2 = cnvxHll arrNG20_
-- Вывод исходных фигур
drwNG arrNG [0, 0, 0] (color 0 255 0) true false 1.0
drwNG arrNG2 [0, 0, 0] (color 0 0 0) true false 1.0
-- Массив с координатами вершин суммы Минковского
arrMS = #()
for k = 1 to arrNG.Count do (
pNG = arrNG[k]
for k2 = 1 to arrNG2.Count do
append arrMS (pNG - arrNG2[k2])
)
cnt = arrMS.Count
-- Вывод вершин массива arrMS
for k = 1 to cnt do point pos: arrMS[k] size:5 box:on wireColor:black
-- Вывод точки в начале координат
point pos:[0, 0, 0] size:20 drawOnTop:on box:on wireColor:brown
-- Создаем массив arrMS_ для построения выпуклой оболочки фигуры A - B
arrMS_ = for k = 1 to cnt collect arrMS[k]
-- Формируем выпуклую оболочку фигуры A - B
-- Алгоритмом GJK эта оболочка не используется
arrNGMS = cnvxHll arrMS_
drwNG arrNGMS [0, 0, 0] (color 0 0 255) true true 1.0
-- Начальный симплекс
ks = random 1 (arrNG.Count - 2)
ks2 = random 1 (arrNG2.Count - 2)
vA1 = arrNG[ks]
vA2 = arrNG[ks + 1]
vA3 = arrNG[ks + 2]
vB1 = arrNG2[ks2]
vB2 = arrNG2[ks2 + 1]
vB3 = arrNG2[ks2 + 2]
v1 = vA1 - vB1
v2 = vA2 - vB2
v3 = vA3 - vB3
arrQ = #(v1, v2, v3)
arrQV = #(#(vA1, vB1, ""), #(vA2, vB2, ""), #(vA3, vB3, ""))
dstAB = -1
kXt = 0
kXtMx = arrNG.Count * arrNG2.Count
--kXtMx = 0
-- Радиус иллюстрационных окружностей
r = 7
thck = 0.5
vN = [0, 0, 0]; vNN = [0, 0, 0]; dMn = 0
arrDlt = #()
vCSO = [0, 0, 0]; vMS = [0, 0, 0]
arrDst1 = #(); arrDst2 = #(); arrDst3 = #()
while dstAB == -1 do (
kXt += 1
-- Защита от возможного зацикливания (может быть снята после завершения отладки)
if kXt > kXtMx do dstAB = 1
-- Сортируем массив по возрастанию y-координаты его элементов
qsort arrQ compareFN k:2
if arrQ.Count == 3 do (
v2 = arrQ[2]
if v2[1] < arrQ[3][1] do (
arrQ[2] = arrQ[3]
arrQ[3] = v2
)
)
-- Вывод симплекса
if prn do drwNG arrQ [0, 0, 0] (color 255 0 0) true false 1.0
-- Проверяем, лежит ли начало координат в пределах симплекса arrQ
if pntrFnd arrQ then (
dstAB = -2
messageBox("Penetration")
)
else (
-- Находим границу симплекса, ближайшую к началу координат
v1 = arrQ[1]
v2 = arrQ[2]
arrDst1 = fndClsPnt v1 v2 arrQ (if arrQ.Count == 3 then arrQ[3] else 0)
if arrQ.Count == 3 then (
v3 = arrQ[3]
arrDst2 = fndClsPnt v2 v3 arrQ v1
arrDst3 = fndClsPnt v3 v1 arrQ v2
dMn = amin arrDst1[3] arrDst2[3] arrDst3[3]
case of (
(dMn == arrDst1[3]): (vN = arrDst1[1]; arrQ = arrDst1[2]; arrDlt = arrDst1[4]; vNN = arrDst1[5])
(dMn == arrDst2[3]): (vN = arrDst2[1]; arrQ = arrDst2[2]; arrDlt = arrDst2[4]; vNN = arrDst2[5])
(dMn == arrDst3[3]): (vN = arrDst3[1]; arrQ = arrDst3[2]; arrDlt = arrDst3[4]; vNN = arrDst3[5])
)
)
else (
vN = arrDst1[1]
arrQ = arrDst1[2]
arrDlt = arrDst1[4]
vNN = arrDst1[5]
)
-- Находим экстремальную точку CSO в направлении от vNN к началу координат
-- как разность экстремальных точек рассматриваемых фигур
vA = fndSCP arrNG -vNN
vB = fndSCP arrNG2 vNN
vCSO = vA - vB
-- Корректировка массива arrQV
arrQV2 = #()
for k = 1 to arrQV.Count do (
vAk = arrQV[k][1]
vBk = arrQV[k][2]
if findItem arrQ (vAk - vBk) > 0 do append arrQV2 #(vAk, vBk, vNN)
)
arrQV = for k = 1 to arrQV2.Count collect arrQV2[k]
if prn do (
circle pos:vA radius:r wireColor:green
circle pos:vB radius:r wireColor:blue
circle pos:vCSO radius:r wireColor:red
circle pos:vNN radius:r wireColor:brown render_renderable:on \
render_displayRenderMesh:on render_thickness:2.0
r += 2
)
if findItem arrQ vCSO + findItem arrDlt vCSO == 0 then (
-- Найдена вершина, улучшающая решение
append arrQ vCSO
append arrQV #(vA, vB)
)
else (
-- Поиск расстояния завершен
dstAB = fndDMn arrQ arrQV vA vB prn
)
)
)
if dstAB > 0 then messageBox("Distance is found")
if dstAB == 0 then messageBox("Distance 0")
format "Iterations amount = %; distance between A and B = %\n" kXt dstAB
Проверка функций, определяющих точку пересечения прямых и коэффициенты нормали к прямой, выполняет приводимый ниже код. Корректность вычислений оценивается по выводимому результату (рис. 9).
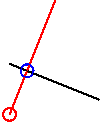
Рис. 9. Рисунок, выводимый отладочным кодом
В программе коэффициентами массива arrCf задается исходная прямая (показана на рис. 9 черным цветом), затем вычисляются коэффициенты прямой, перпендикулярной исходной прямой (показана красной линией). Определяется точка пересечения прямых, в которой выводится синяя окружность.
Также вычисляется расстояние от начальной точки красной линии до ее пересечения с исходной прямой. В начальной точке красной линии выводится красная окружность.
-- Возвращает координаты точки пересечения прямых с коэффициентами,
-- хранимыми массивами arrCf и arrCf2
fn fndVN arrCf arrCf2 = (
local A, B, C, A2, B2, C2, x, y
A = arrCf[1]
B = arrCf[2]
C = arrCf[3]
case of (
-- Вторая прямая проходит через начало координат
-- Прямые перпендикулярны
(A == 0): return point3 0 (-C / B) 0
(B == 0): return point3 (-C / A) 0 0
default: (
A2 = arrCf2[1]
B2 = arrCf2[2]
C2 = arrCf2[3]
bb = B2 / B
x = C * bb / (A2 - A * bb) - C2
y = -(A * x + C) / B
return point3 x y 0
)
)
)
-- Возвращает массив коэффициентов прямой, перпендикулярной прямой,
-- заданной коэффициентами, хранимыми массивом arrCf
fn clcCfNrml arrCf = (
local A, B, C
A = arrCf[1]
B = arrCf[2]
C = arrCf[3]
return if B == 0 then #(0, 1.0, 0) else if A == 0 then #(1.0, 0, 0) else #(-1.0 / (A / B), 1.0, 0)
)
-- Возвращает массив коэффициентов прямой, проходящей через точки v и v2
-- Используем каноническое уравнение прямой Ax + By + C = 0
fn clcCf v v2 = (
x1 = v[1]
y1 = v[2]
x2 = v2[1]
y2 = v2[2]
dx = x2 - x1
dy = y2 - y1
case of (
(dx == 0.0): (A = 1; B = 0; C = -x1)
(dy == 0.0): (A = 0; B = -1; C = y1)
default: (A = dy / dx; B = -1; C = -A * x1 + y1)
)
return #(A, B, C)
)
-- Возвращает расстояние между точкой v3 и прямой, проходящей через точки v и v2
fn dstnc v v2 v3 = (
local arrCf, A, B
arrCf = clcCf v v2
A = arrCf[1]
B = arrCf[2]
return abs(A * v3[1] + B * v3[2] + arrCf[3]) / sqrt (A * A + B * B)
)
-- Рисует линию, проходящую через заданные массивом arrV точки
fn drwLn arrV clr = (
sp = line wireColor:clr render_renderable:on render_displayRenderMesh:on \
render_thickness:1.0
addNewSpline sp
for i = 1 to arrV.Count do (addKnot sp 1 #corner #line arrV[i])
updateShape sp
)
delete $*
-- Массив с коэффициентами первой (исходной) прямой
arrCf = #(2.0, 5.0, 20.0)
A = arrCf[1]
B = arrCf[2]
C = arrCf[3]
-- Массив с коэффициентами второй прямой, которая перпендикулярна исходной прямой
arrCfNrml = clcCfNrml arrCf
A2 = arrCfNrml[1]
B2 = arrCfNrml[2]
-- Координаты точек исходной и найденной прямых
x0 = -15
x = if B == 0 then -C / A else if A == 0 then -15 else x0
y = if A == 0 then -C / B else if B == 0 then -15 else (-A * x - C) / B
x2 = if B2 == 0 then 0 else if A2 == 0 then -15 else x0
y2 = if A2 == 0 then 0 else if B2 == 0 then -15 else -A2 * x2
xx0 = 55
xx = if B == 0 then -C / A else if A == 0 then 15 else xx0
yy = if A == 0 then -C / B else if B == 0 then 15 else (-A * xx - C) / B
xx2 = if B2 == 0 then 0 else if A2 == 0 then 15 else xx0
yy2 = if A2 == 0 then 0 else if B2 == 0 then 15 else -A2 * xx2
v = [x, y, 0]
vv = [xx, yy, 0]
v2 = [x2, y2, 0]
vv2 = [xx2, yy2, 0]
-- Вывод исходной и нормальной к ней прямой
drwLn #(v, vv) (color 0 0 0)
drwLn #(v2, vv2) (color 255 0 0)
-- Находим координаты точки пересечения прямых с коэффициентами,
-- записанными в массивы arrCf и arrCfNrml
vN = fndVN arrCf arrCfNrml
-- Вывод окружности в точке пересечения прямых
circle pos:vN radius:5 wireColor:blue render_renderable:on render_displayRenderMesh:on \
render_thickness:1.0
-- Вывод окружности в точке v2
circle pos:v2 radius:5 wireColor:red render_renderable:on render_displayRenderMesh:on \
render_thickness:1.0
format "Distance from point % to line = %\n" v2 (dstnc v vv v2)