Рассматривается частный случай растровой развертки полигона в окне вывода, когда известны цвета вершин этого полигона. Эти цвета могут быть либо заданы, либо рассчитаны с использованием некоторой модели освещенности.
Так, в 3ds Max полигону можно задать произвольной сложности материал, указать группу сглаживания, в сцене разместить источники света, задать параметры выбранной программы воспроизведения и пр. Далее приложение, а точнее отвечающий за воспроизведение плагин обеспечит расчет цветовых характеристик выводимых полигонов и их отображение в заданных видовых окнах или в окне программы воспроизведения (рис. 1).

Рис. 1. Модифицированная сфера
Для получения рис. 1 можно употребить, например, следующий код:
delete $*
mrbl = marble()
mrbl.coords.Tiling = [7, 7, 1]
std = standard showInViewport:true diffuseMap:mrbl
--meditmaterials[1] = std
sph = sphere radius:30 pos:[0, 0, 0] material:std segs:32 mapcoords:on
convertToPoly sph
move sph.verts[#{1}] [0, 0, -37]
move sph.verts[#{2..33}] [0, 0, -35]
move sph.verts[#{34..65}] [0, 0, -33]
move sph.verts[#{66..97}] [0, 0, -27]
move sph.verts[#{98..129}] [0, 0, -20]
move sph.verts[#{130..161}] [0, 0, -10]
move sph.verts[#{162..193}] [0, 0, -5]
move sph.verts[#{194..225}] [0, 0, -1]
rotate sph (eulerAngles 0 -15 0)
backgroundColor = gray
max quick render
При закраске Гуро рассчитываются RGB-компоненты цвета каждой вершины полигональной модели объекта. Эти значения используются затем для расчета RGB-компонентов при растровой развертке полигонов модели.
Значимым элементом модели освещенности являются нормали к полигонам (рис. 2), расчет которых в 3ds Max зависит от принадлежности полигона к той или иной группе сглаживания.
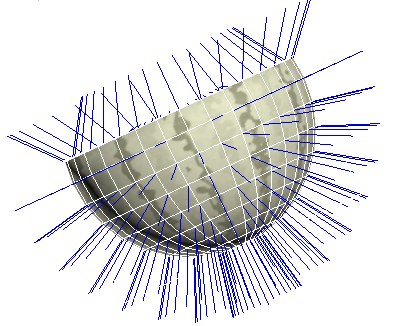
Рис. 2. Объект и его нормали
Нормали рассчитываются в каждой вершине полигона (рис. 3); полученные значения используются затем при расчете цвета вершины.
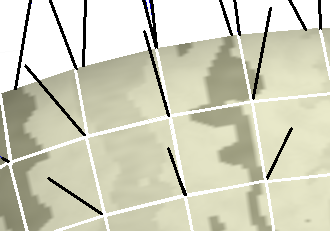
Рис. 3. Все полигоны в одной группе сглаживания: в каждой вершине по одной нормали
Иная картина будет, если полигоны входят в разные группы сглаживания (рис. 4).
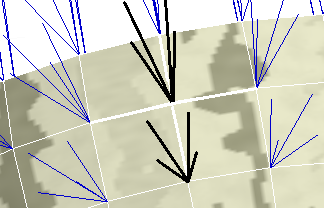
Рис. 4. Групп сглаживания нет: в каждой вершине по 4 нормали
В приводимом далее материале полагается, что известны RGB-компоненты цветов в вершинах полигональной модели объекта и решается задача растровой развертки полигона с интерполяцией его вершинных цветов.
Рассматривается случай выпуклых полигонов.
При интерполяции цветов полагается, что используется прямоугольное проецирование, при котором 3d-точка P(X, Y, Z) отобразится на плоскости проекций в виде точки с координатами x, y:
x = X; y = Y.
Изображение выводится как растровый образ заданного размера, например 200*160 пикселей, создаваемый конструктором bitmap:
btmp = bitmap 200 160 color:white.
Замечание. Рассматриваемый подход является серьезным упрощением схемы преобразований координат, применяемой в графических приложениях.
Механизм интерполяции цветов проиллюстрируем на примере заливки отрезка, одна вершина которого имеет белый цвет, а другая - черный (рис. 5).
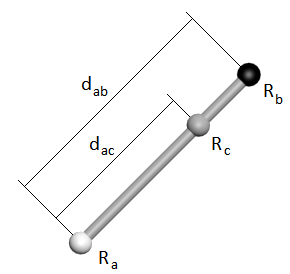
Рис. 5. К расчету R-компоненты цвета в точке Rc выводимого отрезка
fn drawLine p1 p2 prnt = (
l = line render_renderable:off wireColor:black parent:prnt
addNewSpline l
addKnot l 1 #corner #line p1
addKnot l 1 #corner #line p2
updateShape l
)
delete $*
r = 2; h = 40; d = 15; h7 = 0.7 * h
clr = white; clr2 = black
cl = cylinder radius:1 height:h wireColor:gray
sphere radius:r pos:[0, 0, 0] wireColor:clr parent:cl
sphere radius:r pos:[0, 0, h7] wireColor:gray parent:cl
sphere radius:r pos:[0, 0, h] wireColor:clr2 parent:cl
-- Размерные линии
drawLine [0, 0, 0] [-d, 0, 0] cl
drawLine [0, 0, 0.7 * h] [-0.5 * d, 0, h7] cl
drawLine [0, 0, h] [-d, 0, h] cl
drawLine [-0.9 * d, 0, 0] [-0.9 * d, 0, h] cl
drawLine [-0.4 * d, 0, 0] [-0.4 * d, 0, h7] cl
rotate cl (eulerAngles 0 45 0)
Пусть Ra и Rb - значения R-компонент вершин отрезка (используется система цветов RGB).
Рассчитаем значение R-компоненты цвета произвольной точки C отрезка по формуле линейной интерполяции:
Rc = (1 - t) * Ra + t * Rb,
где
t = dac / dab
и
dab - длина выводимого отрезка;
dac - расстояние между А и С.
Последние значения рассчитываются по известным 3d-координатам точек А и С. В случае прямоугольного проецирования X и Y координаты точек А и С и их проекций совпадают.
Выведем для примера растровую развертку отрезка прямой, с толщиной по оси Х в 7 пикселей.
Заметим, что X-координата выводимого отрезка при увеличении Y на 1 изменяется на угловой коэффициент k (x = k * y + b). Поэтому очередная X-координата находится простым суммированием:
x = x + k.
Используем для получения результата следующий код:
delete $*
-- Создаем растровый образ
btmp = bitmap 300 150 color:brown
clrA = white
clrB = black
d = 20
d2 = d + 100
pa = [10, 10, 10]
pb = [290, 140, 100]
xa = pa[1]; ya = pa[2]; za = pa[3]
xb = pb[1]; yb = pb[2]; zb = pb[3]
dx = xb - xa; dy = yb - ya; dz = zb - za
if dy == 0 do messageBox "Error: dy = 0"
k = dx / dy
k2 = sqrt (k * k + 1)
dab = sqrt (dx * dx + dy * dy + dz * dz)
x = xa
y = floor ya
mLL = abs (floor dy)
for n = -3 to 3 do setPixels btmp [x + n, y] #(clrA)
dx = 0
dac = 0
for m = 1 to mLL do (
y += 1
x += k
dac += k2
t = dac / dab
clrC = (1 - t) * clrA + t * clrB
for n = -3 to 3 do setPixels btmp [x + n, y] #(clrC)
)
-- Результат приведен на рис. 6 (используется физическая система координат)
display btmp
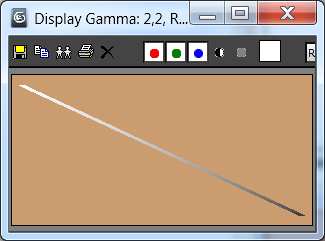
Рис. 6. Растровая развертка отрезка с интерполяцией цветов
Вычисление
dac = sqrt (dx * dx + m * m)
заменено на инкрементную схему:
dac = dac + k2,
в которой
k2 = sqrt (k * k + 1)
(dx = m * k, поэтому dac = m * k2, где значение m нарастает с шагом 1).
В качестве полигона используем четырехугольник (рис. 7), для отображения которого применен следующий код:
fn drawNGn d = (
nGn = line render_renderable:off render_displayRenderMesh:off
seed 2
addNewSpline nGn
addKnot nGn 1 #corner #line (random [0, 0, 0] [-d, d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [-d, -d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [d, -d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [d, d, 0])
close nGn 1
updateShape nGn
convertToPoly nGn
nGn.wireColor = gray
move nGn [d, d, 0]
return nGn
)
delete $*
nGn = drawNGn 60
arrClrs = #(white, yellow, black, [6, 135, 113])
vrts = nGn.verts
for k = 1 to 4 do sphere radius:3 wireColor:arrClrs[k] pos:vrts[k].pos
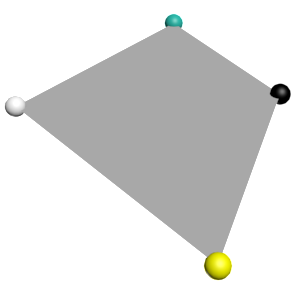
Рис. 6. Вершины полигона показаны в виде сфер (цвет сферы совпадает с цветом вершины)
Входными данными рассматриваемой задачи являются координаты вершин полигона и цвета вершин.
Выполним растровую развертку полигона, используя для расчета цветов пикселей известные цвета вершин, применив следующую последовательность действий:
Замечание. Алгоритм основан на известной схеме растровой развертки выпуклого полигона.
Оформим алгоритм интерполяционной развертки в виде функции fillInNGn, принимающей полигон и массив цветов его вершин.
global yI, xL, xR, kL, kR, kL2, kR2, dabL, dabR, dacL, dacR, btmp
-- Помощник сортировки
fn compareFNY pA pB = (
local d = pA[2] - pB[2]
case of (
(d < 0.0): -1
(d > 0.0): 1
default: 0
)
)
-- Округление числа до целого значения
fn round x = (
fx = floor x
cx = ceil x
return if 0.5 * (fx + cx) > x then fx else cx
)
fn fndDab p1 p2 = (
dx = p2[1] - p1[1]
dy = p2[2] - p1[2]
dz = p2[3] - p1[3]
return sqrt (dx * dx + dy * dy + dz * dz)
)
-- Этап stp заливки (интерполяционной развертки полигона)
fn oneStp yEI clrAL clrBL clrAR clrBR stp = (
while yI < yEI do (
yI += 1
xL += kL
xR += kR
-- Находим цвета пикселей с координатами (xL, YI) и (xR, YI)
dacL += kL2
tL = dacL / dabL
-- Цвет пикселя (xL, YI)
clrL = (1 - tL) * clrAL + tL * clrBL
dacR += kR2
tR = dacR / dabR
-- Цвет пикселя xR, YI
clrR = (1 - tR) * clrAR + tR * clrBR
xLI = round xL
xRI = round xR
dClr = (clrR - clrL) / (xRI - xLI + 1)
clr = clrL
if stp > 0 do for x = xLI to xRI do (
setPixels btmp [x, yI] #(clr)
clr += dClr
)
)
)
fn fillInNGn nGn arrClrs = (
local k, m, pL, pR, pN, pE
nV = nGn.verts.count
arrVs = for k = 1 to nV collect nGn.verts[k].pos
arrVsY = copy arrVs #nomap
qsort arrVsY compareFNY
pMi = arrVsY[1]
pMa = arrVsY[nV]
y = pMi[2]
yI = round y
xL = pMi[1]
xR = xL
k = findItem arrVs pMi
pL = if k == 1 then arrVs[nV] else arrVs[k - 1]
pR = if k == nV then arrVs[1] else arrVs[k + 1]
if pL[1] > pR[1] do (
pT = pL
pL = pR
pR = pT
)
clrPMi = arrClrs[k]
clrAL = clrPMi
clrAR = clrPMi
clrBL = arrClrs[findItem arrVs pL]
clrBR = arrClrs[findItem arrVs pR]
kL = (xL - pL[1]) / (y - pL[2])
kR = (xR - pR[1]) / (y - pR[2])
kL2 = sqrt (kL * kL + 1)
kR2 = sqrt (kR * kR + 1)
dabL = fndDab pMi pL
dabR = fndDab pMi pR
dacL = 0
dacR = 0
for stp = 1 to nV do (
yE = amin pL[2] pR[2]
if yE == pL[2] then (
pE = pL
pN = pR
)
else (
pE = pR
pN = pL
)
-- Очередной шаг растровой развертки полигона
oneStp (round yE) clrAL clrBL clrAR clrBR stp
if yE == pMa[2] do exit
m = findItem arrVs pE
pE1 = if m == 1 then arrVs[nV] else arrVs[m - 1]
pE2 = if m == nV then arrVs[1] else arrVs[m + 1]
pEN = if pE2[2] > pE1[2] then pE2 else pE1
-- Угловой коэффициент kE линии между вершинами pE и pEN
kE = (pEN[1] - pE[1]) / (pEN[2] - pE[2])
kE2 = sqrt (kE * kE + 1)
clrBN = arrClrs[findItem arrVs pEN]
dabN = fndDab pE pEN
if pN == pL then (
pR = pEN
clrAR = clrBR
clrBR = clrBN
kR = kE
kR2 = kE2
dacR = 0
dabR = dabN
)
else (
pL = pEN
clrAL = clrBL
clrBL = clrBN
kL = kE
kL2 = kE2
dacL = 0
dabL = dabN
)
)
)
fn drawNGn d = (
nGn = line render_renderable:off render_displayRenderMesh:off
seed 2
addNewSpline nGn
addKnot nGn 1 #corner #line (random [0, 0, 0] [-d, d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [-d, -d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [d, -d, 0])
addKnot nGn 1 #corner #line (random [0, 0, 0] [d, d, 0])
close nGn 1
updateShape nGn
convertToPoly nGn
nGn.wireColor = gray
move nGn [d, d, 0]
return nGn
)
-- Основная программа (поверка процедур интерполяционной заливки полигона)
delete $*
w = 200
h = 160
-- Создаем растровую карту белого цвета
btmp = bitmap w h color:white
-- Генерируем полигон (четырехугольник)
nGn = drawNGn 80
-- Задаем цвета вершин четырехугольника
arrClrs = #(gray, yellow, black, brown)
--arrClrs = #(black, white, black, white)
---
vrts = nGn.verts
for k = 1 to 4 do sphere radius:3 wireColor:arrClrs[k] pos:vrts[k].pos
--
-- Интерполяционная развертка многоугольника
fillInNGn nGn arrClrs
-- Отображение результата (см. рис. 8)
display btmp
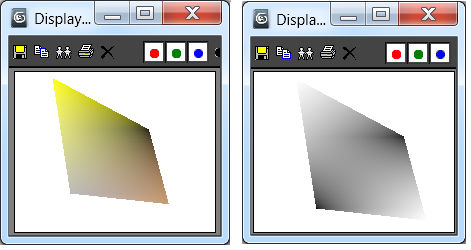
Рис. 8. Интерполяционная развертка полигона с наборами цветов вершин:
gray, yellow, black, brown и black, white, black, white
Та же, что и описанная выше схема, используется при закраске Гуро, с той разницей, что цвета вершин рассчитываются по правилам, определенным моделью освещения. Сами же модели создаются исходя о физических представлениях о природе света, свойств материала, влияющих на отражение, преломление и в ряде случаях на излучение света.