Список работ

Реализация схемы наложения текстуры

Содержание

• Введение
• Примеры текстурирования в 3ds Max
• Схема наложения текстуры
• Генерация текстуры
• Вывод сторон полигона
• Заливка полигона
• Расчетные формулы
• Наложение текстуры
• Заключение
• Литература

ВВЕДЕНИЕ

Рассматривается схема наложения текстуры на полигон при прямоугольном проецировании.
При таком проецировании 3d-точка P(X, Y, Z) отобразится на плоскости проекций в виде точки с координатами x, y

x = X; y = Y.

Реализация рассматриваемой схемы текстурирования выполнена средствами MAXScript. Изображение выводится как растровый образ размера 200*170 пикселей, создаваемый конструктором bitmap:

btmp = bitmap 200 170 color:white.

Замечание. Рассматриваемый подход является серьезным упрощением схемы преобразований координат, применяемой в графических приложениях.

ПРИМЕРЫ ТЕКСТУРИРОВАНИЯ В 3DS MAX

Текстура - это объект, генерирующий растровую карту текстуры, окончательный вид которой зависит от исходного образа и параметров текстуры (координат текстуры).
В 3ds Max ссылка на текстуру используется при определении значения карты материала, например:

delete $*
-- Создаем стандартный материал
std = standard showInViewport:true
-- Создаем текстуру Checker, используя одноименный конструктор
chck = Checker()
-- Задаем карту диффузионной составляющей созданного материала
std.diffuseMap = chck
-- Рисуем плоскость с 16-ю полигонами
pln = plane length:50 width:80 pos:[0, 0, 0] lengthSegs:4 widthSegs:4
-- Определяем материал плоскости
pln.material = std

По умолчанию в случае плоскости текстура накладывается в 3ds Max на все ее полигоны (рис. 1).

Рис. 1. Текстура Checker на плоскости с 16 полигонами (U_Tiling = V_Tiling = 4)

Координаты u, v текстуры изменяются в диапазоне [0, 0] - [1, 1]. Координатами можно управлять, регулируя такие свойства координат текстуры, как Offset (отступ), Tiling (повтор), Angle (угол) и др. Изменив, например, Tiling:

chck.coords.U_Tiling = 4
chck.coords.V_Tiling = 4

получим иное воспроизведение текстуры на тоже плоскости (рис. 2).

Рис. 2. Текстура Checker (U_Tiling = V_Tiling = 4)

Наложим теперь текстуру Checker с тем же tiling-значениями на невыпуклый многоугольник:

delete $*
-- Создаем текстуру Checker, используя одноименный конструктор
chck = Checker()
chck.coords.U_Tiling = 4
chck.coords.V_Tiling = 4
-- Создаем стандартный материал и задаем его диффузионную карту
std = standard showInViewport:true diffuseMap:chck
-- Создаем невыпуклый многоугольник
nGn = line()
addNewSpline nGn
addKnot nGn 1 #corner #line [-60, -20, 0]
addKnot nGn 1 #corner #line [-20, 40, 0]
addKnot nGn 1 #corner #line [20, 40, 0]
addKnot nGn 1 #corner #line [30, -30, 0]
addKnot nGn 1 #corner #line [-10, 0, 0]
close nGn 1
updateShape nGn
-- Преобразуем сплайн в полигон
convertToPoly nGn
update nGn
-- Обеспечим возможность генерации координат текстуры
addModifier nGn (unwrap_UVW())
-- Определяем материал многоугольника; результат приведен на рис. 3
nGn.material = std

Рис. 3. Текстура Checker на невыпуклом многоугольнике с одним полигоном

СХЕМА НАЛОЖЕНИЯ ТЕКСТУРЫ

Пусть в пространстве задана 4-угольный полигон P₁, P₅, P₄, P₆, ограниченный прямоугольником P₁, P₂, P₃, P₄ (рис. 4).

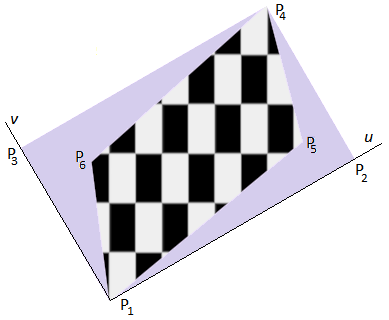
Рис. 4. Полигон с обрамляющим прямоугольником и наложенной текстурой Checker

Для получения рис. 4 употреблен следующий код:

delete $*
-- Вывод прямоугольника P₁, P₂, P₄, P₃
pln = plane length:50 width:80 pos:[0, 0, 0] lengthSegs:1 widthSegs:1
rotate pln (eulerAngles 0 0 30)
convertToPoly pln
p1 = pln.verts[1].pos
move pln -p1
p1 = pln.verts[1].pos
p2 = pln.verts[2].pos
p3 = pln.verts[3].pos
p4 = pln.verts[4].pos
x5 = p2[1] - 15
x6 = p3[1] + 20
y5 = p2[2] + 5
y6 = p3[2] - 4
-- Вывод четырехугольника P₁, P₅, P₄, P₆
nGn = line render_renderable:off render_displayRenderMesh:off wireColor:black
addNewSpline nGn
addKnot nGn 1 #corner #line p1
addKnot nGn 1 #corner #line [x5, y5, 0]
addKnot nGn 1 #corner #line p4
addKnot nGn 1 #corner #line [x6, y6, 0]
close nGn 1
updateShape nGn
-- Преобразование сплайна в полигон и его текстурирование средствами 3ds Max
convertToPoly nGn
chck = Checker()
chck.coords.U_Tiling = 4; chck.coords.V_Tiling = 3
std = standard showInViewport:true diffuseMap:chck
addModifier nGn (unwrap_UVW())
nGn.material = std

Свяжем прямоугольник P₁, P₂, P₄, P₃ с системой координат текстуры, полагая, что координаты u, v изменяются в диапазоне [0, 1].
Пусть также имеется растровый образ (рис. 5), на основе которого должна быть создана текстура.

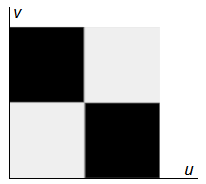
Рис. 5. Образ, используемый при создании текстуры

Кроме того, пусть заданы tiling-параметры координат текстуры, например u_tiling = 4, а v_tiling = 3. Зная эти параметры, несложно создать текстуру (рис. 6).

Рис. 6. Текстура, которую следует нанести на полигон P₁, P₅, P₄, P₆

Если размер исходного образа (см. рис. 5) равен 32*32, то размер приведенный на рис. 6 текстуры будет равен 128*96. При этом диапазон изменения координат текстуры остается тем же: [0, 1].

Задача текстурирования в том, чтобы каждой точке x, y (каждому пикселю) проекции полигона поставить в соответствие точку u, v созданной текстуры и использовать RGB-компоненты этой точки для закраски соответствующего пикселя экрана (x и y берутся в оконной системе координат).
Таким образом, программа наложения текстуры должна обеспечить:

1. Генерацию текстуры (выполняется по исходному образу с учетом параметров текстуры).
2. Сканирование пикселей проекции полигона.
3. Поиск для каждого пикселя, соответствующей точки на текстуре.
4. Закраску текущего пикселя изображения цветом найденной точки текстуры.

Наиболее трудоемким является 3-й этап приведенной схемы.

ГЕНЕРАЦИЯ КАРТЫ ТЕКСТУРЫ

Взятую для примера текстуру (см. рис. 6), несложно создать программно.

fn oneRow txtr w h s ny ns ys xs = (
 y = ys
 for n = ns to ny by 2 do (
  sy = if y + s > h then h - y else s
  y2 = 0
  while y2 < sy do (
   x = xs
   while x < w do (
    sx = if x + s > w then w - x else s
    for k = 1 to sx do (
     setPixels txtr [x, y + y2] #([0, 0, 0])
     x += 1
    )
    x += sx
   )
   y2 += 1
  )
  y += 2 * sy
 )
)
fn txtrGnrtn w h s = (
 txtr = bitmap w h color:white
 ny = (h / s) as integer
 ny += if h / s > ny then 1 else 0
 oneRow txtr w h s ny 1 0 0
 oneRow txtr w h s ny 2 s s
 return txtr
)
txtr = txtrGnrtn (32 * 4) (32 * 3) (32 / 2)
display txtr -- Результат приведен на рис. 7

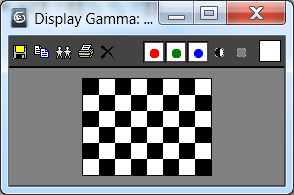
Рис. 7. Программно сгенерированная карта текстуры размером 128*96 пикселей

Отличие рис. 7 от рис. 6 объясняется тем, что при работе с растровым образом используется физическая система координат, в которой начало координат находится в левом верхнем углу образа.

ВЫВОД СТОРОН ПОЛИГОНА

Стороны полигонов выводятся функцией ptLn с использованием алгоритма Брезенхейма для 8-связной развертки отрезка [2]
(алгоритм приведен в конце этого раздела):

fn ptLn pa pb clr btmp = (
 xa = pa[1] as integer
 ya = pa[2] as integer
 xb = pb[1] as integer
 yb = pb[2] as integer
 dx = xb - xa
 dy = yb - ya
 incX = if dx > 0 then 1 else -1
 incY = if dY > 0 then 1 else -1
 dx = abs dx; dy = abs dy
 d = if dy > dx then dy else dx
 errX = 0; errY = 0
 setPixels btmp [xb, yb] #(clr)
 while xa != xb or ya != yb do (
  setPixels btmp [xa, ya] #(clr)
  errX += dx; errY += dy
  if errX >= d do (
   errX -= d
   xa += incX
  )
  if errY >= d do (
   errY -= d
   ya += incY
  )
 )
)
fn getVs = (
 -- Получаем координаты вершин P1, P2, P4, P3
 pln = plane length:100 width:160 pos:[0, 0, 0] lengthSegs:1 widthSegs:1
 rotate pln (eulerAngles 0 0 25)
 -- Преобразование в полигон
 convertToPoly pln
 p1 = pln.verts[1].pos
 move pln [0, -p1[2] + 5, 0]
 p3 = pln.verts[3].pos
 move pln [-p3[1] + 5, 0, 0]
 p1 = pln.verts[1].pos; p2 = pln.verts[2].pos; p3 = pln.verts[3].pos; p4 = pln.verts[4].pos
 -- Получаем координаты вершин P5 и P6
 x5 = p2[1] - 15; x6 = p3[1] + 20
 y5 = p2[2] + 5; y6 = p3[2] - 4
 p5 = [x5, y5]; p6 = [x6, y6]
 return #(p1, p2, p3, p4, p5, p6)
)
delete $*
arrVs = getVs()
btmp = bitmap 200 170 color:white
clr = (color 0 0 0)
-- Вывод полигонов (рис. 9)
-- Прямоугольник
ptLn arrVs[1] arrVs[2] clr btmp
ptLn arrVs[1] arrVs[3] clr btmp
ptLn arrVs[2] arrVs[4] clr btmp
ptLn arrVs[3] arrVs[4] clr btmp
-- Четырехугольник
ptLn arrVs[1] arrVs[5] clr btmp
ptLn arrVs[1] arrVs[6] clr btmp
ptLn arrVs[5] arrVs[4] clr btmp
ptLn arrVs[6] arrVs[4] clr btmp
display btmp

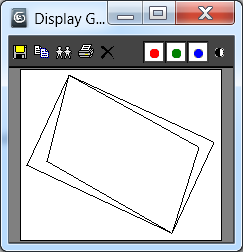
Рис. 8. Для вывода сторон полигонов употреблен алгоритм Брезенхейма

Замечания:

1. В итоговом коде, обеспечивающем наложение текстуры, при выводе сторон четырехугольника данный алгоритм не используется. Взамен берутся точки пересечения текущего ряда растрового образа с линиями, задающими стороны выводимого полигона.
2. В алгоритме Брезенхейма при построении растрового изображения отрезка на линии x = const, проводимой по центру пикселя, всегда выбирается ближайший по вертикали пиксель (рис. 9).

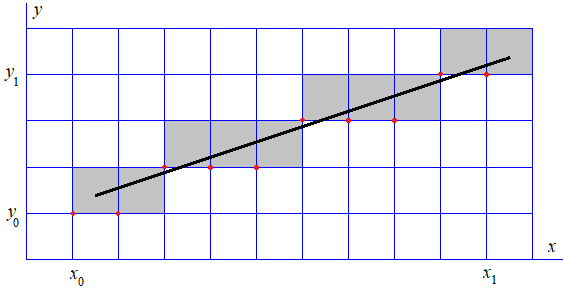
Рис. 9. Алгоритм Брезенхейма: 8-связная развертка отрезка

Для вывода рис. 9 (без заливки) можно употребить следующий код:

fn drawLine ss k p1 p2 = (
 addNewSpline ss
 addKnot ss k #corner #line p1
 addKnot ss k #corner #line p2
 updateShape ss
)
delete $*
d = 20
sL = 4; sW = 10
L = sL * d; w = sW * d
dL = L / sL; dW = w / sW
x = (0.5 * sW - 1) * dW + 0.5 * dW; y = (0.5 * sL - 1) * dL + 0.5 * dL
pln = plane width:w length:L pos:[0, 0, -1] lengthSegs:sL widthSegs:sW wireColor:blue
ss = line render_renderable:on wireColor:black
drawLine ss 1 [-x, -y, 0] [x, y, 0] pos:[0, 0, 0]
move ss [0, -0.125 * dW, 0]

Алгоритм Брезенхейма для первого квадранта:
Входные данные:
(x₀, y₀); (x₁, y₁) - координаты начального и конечного пикселей отрезка (см. рис. 9).

1. Начало.
2. dx = x1 - x0
3. dy = y1 - y0
4. D = 2 * dy - dx
5. x = x0
6. y = y0
7. Пока x < x1 Цикл
       Вывести пиксель (x, y)
       Если D > 0 Тогда
           y = y + 1
           D = D - 2 * dx
       КонецЕсли
       D = D + 2 * dy
       x = x + 1
   КонецЦикла
8. Останов.

ЗАЛИВКА ПОЛИГОНА

Отметим прежде, что X-координата выводимой стороны полигона при увеличении Y на 1 изменяется на угловой коэффициент k соответствующего уравнения прямой (x = k *  y + b). Поэтому очередная X-координата находится простым суммированием:

x = x + k

Заливка заданным цветом выпуклого многоугольника выполняется по следующей схеме:

1. Найти вершины pMi и pMa многоугольника с минимальной и максимальной Y-координатами.
2. y = pMi[2]; xL = pMi[1]; xR = xL.
3. Найти вершины pL и pR, смежные с pMi (pL[1] < pR[1]).
4. Вычислить угловые коэффициенты kL и kR линий, выводимых сторон многоугольника.
5. yE = min(pL[2], pR[2]).
6. Если yE = pL[2] Тогда
    pE = pL
    pN = pR
   Иначе
    pE = pR
    pN = pL
   КонецЕсли.
7. Пока y < yE Цикл
    y = y + 1
    -- Находим точки пересечения линии Y со сторонами полигона
    xL = xL + kL
    xR = xR + kR
    Залить отрезок между xL и xR заданным цветом.
   КонецЦикла
   
8. Если yE = pMa[2] Тогда
    Останов.
   КонецЕсли.
9. Найти вершину pEN, следующую за вершиной pE.
10. Вычислить угловой коэффициент kE линии между вершинами pE и pEN.
11. Если pN == pL Тогда
     pR = pEN
     kR = kE
    Иначе
     pL = pEN
     kL = kE
    КонецЕсли
12. Перейти к п. 5

Согласно схеме на каждом этапе выпуклый многоугольник заливается начиная с некоторого значения Y до ближайшей по Y вершины pE. После достижения этой вершины определяется смежная с ней вершина pEN (не пройденная), рассчитывается угловой коэффициент прямой, проходящей через pE и pEN, и выполняется следующий этап заливки, либо заливка прекращается, если все вершины пройдены.
Оформим приведенную схему в виде функции fillInNGn, принимающей полигон и цвет заливки.

global y, xL, xR, kL, kR, btmp
-- Помощник сортировки
fn compareFNY pA pB = (
 local d = pA[2] - pB[2]
 case of (
 (d < 0.0): -1
 (d > 0.0): 1
 default: 0
 )
)
-- Округление числа до целого значения
fn round x = (
 fx = floor x
 cx = ceil x
 return if 0.5 * (fx + cx) > x then fx else cx
)
-- Этап заливки (растровой развертки полигона) с номером stp
fn oneStp yE clr stp = (
 while y < yE do (
  y += 1
  xL += kL
  xR += kR
  xLI = round xL
  xRI = round xR
  if stp > 0 do for x = xLI to xRI do setPixels btmp [x, y] #(clr)
 )
)
fn fillInNGn nGn clr = (
 local k, m, pL, pR
 nV = nGn.verts.count
 arrVs = for k = 1 to nV collect nGn.verts[k].pos
 arrVsY = copy arrVs #nomap
 qsort arrVsY compareFNY
 pMi = arrVsY[1]
 pMa = arrVsY[nV]
 y = pMi[2]
 xL = pMi[1]
 xR = xL
 k = findItem arrVs pMi
 pL = if k == 1 then arrVs[nV] else arrVs[k - 1]
 pR = if k == nV then arrVs[1] else arrVs[k + 1]
 if pL[1] > pR[1] do (
  pT = pL
  pL = pR
  pR = pT
 )
 kL = (xL - pL[1]) / (y - pL[2])
 kR = (xR - pR[1]) / (y - pR[2])
 for stp = 1 to nV do (
  yE = amin pL[2] pR[2]
  if yE == pL[2] then (
   pE = pL
   pN = pR
  )
  else (
   pE = pR
   pN = pL
  )
  oneStp yE clr stp
  if yE == pMa[2] do exit
  m = findItem arrVs pE
  pE1 = if m == 1 then arrVs[nV] else arrVs[m - 1]
  pE2 = if m == nV then arrVs[1] else arrVs[m + 1]
  pEN = if pE2[2] > pE1[2] then pE2 else pE1
  -- Угловой коэффициент kE линии между вершинами pE и pEN
  kE = (pEN[1] - pE[1]) / (pEN[2] - pE[2])
  if pN == pL then (
   pR = pEN
   kR = kE
  )
  else (
   pL = pEN
   kL = kE
  )
 )
)
-- Формирование четырехугольника
fn drawNGn nGn k p1 p2 p3 p4 = (
 addNewSpline nGn
 addKnot nGn k #corner #line p1
 addKnot nGn k #corner #line p2
 addKnot nGn k #corner #line p3
 addKnot nGn k #corner #line p4
 close nGn 1
 updateShape nGn
)
fn dfnPlgn d ngl clr sd sM = (
 -- Затравка датчика случайных чисел
 seed sd
 -- Генерируем координаты полигона
 p1 = random [0, 0, 0] [-d, d, 0]
 p2 = random [0, 0, 0] [-d, -d, 0]
 p3 = random [0, 0, 0] [d, -d, 0]
 p4 = random [0, 0, 0] [d, d, 0]
 -- Формируем четырехугольник
 nGn = line render_renderable:off render_displayRenderMesh:off wireColor:clr
 drawNGn nGn 1 p1 p2 p3 p4
 convertToPoly nGn
 rotate nGn (eulerAngles ngl ngl 0)
 move nGn [sM, sM, 0]
 return nGn
)
-- Основная программа (поверка процедур заливки полигона)
delete $*
w = 200
h = 150
-- Создаем растровую карту белого цвета
btmp = bitmap w h color:white
-- Генерируем полигон (четырехугольник) и выполняем его сдвиг и поворот
nGnR = dfnPlgn 50 15 red 2 60
-- Растровая развертка многоугольника; при выводе полигон заливается красным цветом
fillInNGn nGnR red
-- Отображение результата (см. рис. 10)
display btmp

Рис. 10. Заливка полигона

РАСЧЕТНЫЕ ФОРМУЛЫ

Приводятся формулы, обеспечивающие реализацию 3-го пункта вышеприведенной схемы текстурирования.
При прямоугольном проецировании точка P(X, Y, Z) отобразится на плоскости проекций в точку с координатами x, y:

x = X; y = Y.

Вернемся к рис. 4 и введем следующие векторы:

a = P₁; e₁ = P₂ - P₁; e₂ = P₃ - P₁.

Тогда в системе координат u, v координаты произвольной точки

P(X, Y, Z) = a + u * e₁ + v * e₂.

Тогда координаты x, y этой точки картинной плоскости соответственно равны:

x = a_x + u * e_1x + v * e_2x;
y = a_y + u * e_1y + v * e_2y.

Решая эту систему относительно u и v, применяя правило Крамера, получим

u = Δ_u / Δ; v = Δ_v / Δ,

где

Δ = e_1x * e_2y - e_1y * e_2x
Δ_u = (x - a_x) * e_2y - (y - a_y) * e_2x
Δ_v = (y - a_y) * e_1x - (x - a_x) * e_1y

Заметим, что координаты u, v находятся в диапазоне [0, 1].
Тогда пиксель с координатами x, y при наложении приведенной на рис. 7 текстуры (ее размер равен 128*96) следует закрасить следующим цветом:

clr = getPixels txtr [128 * u, 96 * v] 1

НАЛОЖЕНИЕ ТЕКСТУРЫ

Приводится код, обеспечивающий наложение текстуры на выпуклый четырехугольник. Результат отображается в виде растрового образа.
При выводе рисунка, для каждого ряда растрового образа, начиная с вершины с меньшей y-координаты, выполняются следующие действия:

• определяются точки xL, xR пересечения линии Y, отвечающей текущему ряду растрового образа, со сторонами четырехугольника;
• закрашиваются черным цветом пиксели с координатами (xLI, Y) и (xRI, Y) (вывод сторон полигона), где xLI и xRI - это целые числа, равные округленным значениям xL и xR;
• определяются u, v координаты на отрезке (xLI + 1, Y) и (xRI - 1, Y) и в соответствии с текстурой закрашиваются пиксели исследуемого отрезка (см. цикл for в функции oneStep).

Алгоритм вывода полигона приведен в разд. Заливка полигона.

global y, xL, xR, kL, kR, txtr, btmp
-- Помощник сортировки
fn compareFNY pA pB = (
 local d = pA[2] - pB[2]
 case of (
 (d < 0.0): -1
 (d > 0.0): 1
 default: 0
 )
)
-- Округление числа до целого значения
fn round x = (
 fx = floor x
 cx = ceil x
 return if 0.5 * (fx + cx) > x then fx else cx
)
-- Этап заливка с номером stp
fn oneStp2 ax ay e1x e1y e2x e2y dt yE stp = (
 while y < yE do (
  y += 1
  xL += kL
  xR += kR
  xLI = round xL
  xRI = round xR
  setPixels btmp [xLI, y] #(black)
  setPixels btmp [xRI, y] #(black)
  -- if stp == 3 do (
  for x = xLI + 1 to xRI - 1 do (
    u = ((x - ax) * e2y - (y - ay) * e2x) / dt
    v = ((y - ay) * e1x - (x - ax) * e1y) / dt
    clr = getPixels txtr [128 * u, 96 * v] 1
    setPixels btmp [x, y] clr
  )
  --)
 )
)
fn fillInNGn2 arrVsLL = (
 local k, m, pL, pR
 p1 = arrVsLL[1]
 p2 = arrVsLL[2]
 p3 = arrVsLL[3]
 p4 = arrVsLL[4]
 p5 = arrVsLL[5]
 p6 = arrVsLL[6]
 arrVs = #(p1, p5, p4, p6)
 arrVsY = copy arrVs #nomap
 qsort arrVsY compareFNY
 --
 ax = p1[1]; ay = p1[2]
 e1 = p2 - p1
 e2 = p3 - p1
 e1x = e1[1]; e1y = e1[2]; e2x = e2[1]; e2y = e2[2]
 dt = e1x * e2y - e1y * e2x
 --
  nV = arrVs.count
  pMi = arrVsY[1]
  pMa = arrVsY[nV]
  y = pMi[2]; xL = pMi[1]; xR = xL
  k = findItem arrVs pMi
  pL = if k == 1 then arrVs[nV] else arrVs[k - 1]
  pR = if k == nV then arrVs[1] else arrVs[k + 1]
  if pL[1] > pR[1] do (
  pT = pL
  pL = pR
  pR = pT
 )
 kL = (xL - pL[1]) / (y - pL[2])
 kR = (xR - pR[1]) / (y - pR[2])
 for stp = 1 to 3 do (
  yE = amin pL[2] pR[2]
  if yE == pL[2] then (
   pE = pL
   pN = pR
  )
  else (
   pE = pR
   pN = pL
  )
  oneStp2 ax ay e1x e1y e2x e2y dt yE stp
  m = findItem arrVs pE
  pE1 = if m == 1 then arrVs[nV] else arrVs[m - 1]
  pE2 = if m == nV then arrVs[1] else arrVs[m + 1]
  pEN = if pE2[2] > pE1[2] then pE2 else pE1
  kE = (pEN[1] - pE[1]) / (pEN[2] - pE[2])
  if pN == pL then (
   pR = pEN
   kR = kE
  )
  else (
   pL = pEN
   kL = kE
  )
 )
)
-- Основная программа
delete $*
-- Код функций txtrGnrtn и oneRow см. выше
txtr = txtrGnrtn (32 * 4) (32 * 3) (32 / 2)
btmp = bitmap 200 170 color:white
-- Получаем вершины четырехугольника
-- Код функции getVs см. выше
arrVsLL = getVs()
-- Наложение текстуры
fillInNGn2 arrVsLL
display btmp

Отдельные этапы наложения текстуры и конечный результат показаны на рис. 12.

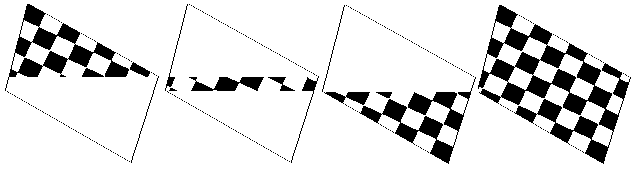
Рис. 11. Три этапа наложения текстуры и конечный результат

ЗАКЛЮЧЕНИЕ

В примере использован упрощенный подход к задачам вывода изображения и наложения текстуры. Этим и объясняется отличие результатов, приведенных на рис. 4 и рис. 11.
В [2] приведена схема наложения текстуры при перспективном проецировании объекта (также упрощенный вариант). Центр проецирования (рис. 12) находится в начале координат, а плоскость проекций (картинная плоскость) удалена на единицу от начала координат (z = 1).

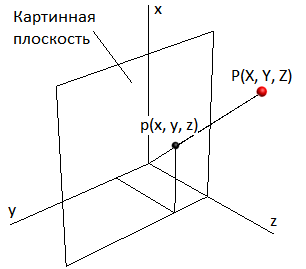
Рис. 12. Упрощенная схема центрального проецирования

Кроме того, z-координаты проецируемого объекта больше 1.
При таком проецировании 3d-точка P(X, Y, Z) отобразится на плоскости проекций в виде точки с координатами x, y:

x = X / Z; y = Y / Z.

Применение центрального проецирования влечет рост объема вычислений, но не меняет схему наложения текстуры.
Также в [2] рассматриваются интерполяционные, применяемые на практике методы наложения текстуры, обеспечивающие снижение времени вычислений и сохраняющие приемлемое качество результата.

Замечание. Для вывода рис. 12 (без надписей) можно употребить следующий код:

fn drawLine ss k p1 p2 = (
 addNewSpline ss
 addKnot ss k #corner #line p1
 addKnot ss k #corner #line p2
 updateShape ss
)
delete $*
pC = [0, 0, 0]
d = 50
d2 = d / 2
d3 = 0.75 * d
r = 1
ss = line render_renderable:off wireColor:black; drawLine ss 1 pC [-d, 0, 0]
ss = line wireColor:black; drawLine ss 1 pC [0, -d, 0]
ss = line wireColor:black; drawLine ss 1 pC [0, 0, d]
rctngl = rectangle width:50 length:50 pos:[-d2, -d2, d2] wireColor:black
rotate rctngl (eulerangles -90 0 0)
p0 = [-12.8, -25.2, 21.1]
p1 = [-d3, -1.5 * d, 1.25 * d]
sphere radius:r pos:p1 wireColor:red
ss = line wireColor:black; drawLine ss 1 pC p1
sphere radius:r pos:p0 wireColor:black
ss = line wireColor:black; drawLine ss 1 p0 p1
p2 = p0 - [0, 0, p0[3]]
ss = line wireColor:black; drawLine ss 1 p0 p2
p3 = p2 -[0, p2[2], 0]
ss = line wireColor:black; drawLine ss 1 p2 p3

ЛИТЕРАТУРА

1. Autodesk® 3ds Max® 2009 MAXScript Reference.
2. Шикин Е. В., Боресков А. В. Компьютерная графика. Динамика, реалистические изображения. - М.: Диалог-МИФИ, 1995. - 288 с.

Список работ