В задачах компьютерного зрения при анализе изображений зачастую необходимо выделять в изображении различные кривые (прямые, окружности и т.д.). Для решения данной задачи существует целое семейство методов, основанных на преобразовании Хафа. Теоретические возможности этого преобразования позволяют не ограничиваться плоскостью и дискретными кривыми, его можно применять для поиска кривых в облаке точек на плоскости или в многомерном пространстве. Однако практическое применение преобразования Хафа затрудняется высокой сложностью алгоритма, как по времени, так и по памяти, поэтому большинство модификаций метода направлено на его ускорение.
Целью курсового проекта является разработка приложения, позволяющего векторизовать растровые изображения методом Хафа.
Пусть дано облако точек в пространстве Rm
X = {x1, …, xn}
и семейство параметрически заданных кривых
F(φ, x) = 0
где F – некоторая функция, φ – вектор параметров семейства кривых, x – координаты точек из Rm. Каждое значение φ определяет одну кривую, а все множество значений φ образует фазовое пространство Ф кривых данного семейства.
В силу конечного объема памяти и дискретного машинного представления мы не можем рассматривать каждое значение φ в отдельности, поэтому фазовое пространство Ф разбивается на ячейки, для чего вводится регулярная сетка с заданным шагом дискретизации. Каждой ячейке ставится в соответствие счетчик. Набор всех счетчиков называется аккумулятором. Любая ячейка задаёт множество кривых, а значение счетчика ячейки определяется количеством точек из облака X, лежащих хотя бы на одной из этих кривых. Тогда если все точки из X лежат на одной кривой с параметром φ0, то в соответствующей ячейке значение счетчика будет максимально.
Базовый алгоритм выделения кривых состоит из следующих шагов:
Дискретизация.
На шаге 1 мы выбираем сетку дискретизации. В связи с этим выбором возможны следующие проблемы:
Сложность алгоритма.
Заполнение аккумулятора на шаге 2 является самой трудоёмкой частью алгоритма, сложность которой зависит от размерности фазового пространства и сетки дискретизации. Чем больше размерность Ф и меньше сетка, тем больше ячеек в аккумуляторе. Значит, тем больше требуется памяти и времени для его хранения и заполнения. Именно поэтому на практике чаще всего фазовое пространство представляет собой плоскость, а преобразование Хафа применяется в основном для поиска прямых на плоскости.
В связи с вышеперечисленными проблемами были разработаны модификации стандартного алгоритма (Standard Hough Transform).
Эта модификация разрабатывалась для быстрого поиска прямых линий на изображении. В таком случае у нас имеется плоское бинарное изображение (на нём точки интереса одного цвета, а точки фона другого). Поскольку производится поиск прямых линий, то размерность фазового пространства равна 2.
Идея метода состоит в изменении шага 2 (заполнение аккумулятора):
Первый шаг модификации необходим для сокращения числа переборов.
Если точек в участке мало и сетка дискретизации фазового пространства тоже мала, количество записей в аккумуляторе получается меньше.
Это еще одна модификации для поиска линий на бинарном изображении.
Идея метода:
В результате сложность алгоритма снижается за счет разбиения изображения (можно использовать более грубую сетку в фазовом пространстве).
Недостаток в том, что одна длинная линия может быть в результате представлена несколькими близкими линиями, поскольку разные концы отрезка могут быть неколлинеарными при близком рассмотрении, то есть на низких уровнях иерархического слияния.
Эта модификация позволяет использовать меньше места для хранения аккумулятора и быстрее выделять кривые. На протяжении всего процесса поиска используется аккумулятор заранее выбранного маленького размера, например, 9*9 или 3*3*3*3 в многомерном случае.
Алгоритм выглядит следующим образом:
Главными достоинствами являются:
Главный недостаток:
Если исходное облако точек X образует несколько кривых из заданного семейства, то для выделения каждой необходимо повторить весь алгоритм сначала (предварительно выкинув из рассмотрения точки уже выделенных кривых).
В этой модификации алгоритма рассматривается только доля α точек из X, при этом результат с некоторой вероятностью получается такой же, как и у стандартного алгоритма. Доля точек выбирается случайно с равномерной вероятностью.
Показано, что существует αthreshold, такое, что при α > αthreshold ошибок (относительно стандартного алгоритма) происходит очень мало, а при α < αthreshold их количество резко возрастает. Поэтому рекомендуется выбирать α примерно равное αthreshold, которое находится в диапазоне 5 – 15% от всего количества точек.
Очевидное достоинство модификации заключается в сокращении перебора на шаге 2.
И также очевиден недостаток – недетерминированность результата относительно входных данных.
Пусть имеется облако точек X и большое количество точек образуют искомую кривую. Тогда в соответствующей ячейке фазового пространства значение счетчика будет иметь большое значение. Идея этой модификации заключается в том, чтобы выделять кривые (шаг 4) при достижении счетчиком порогового значения, не заполняя аккумулятор полностью (шаг 2). Для вышеописанной кривой значение соответствующего счетчика довольно быстро наберет пороговое значение.
Алгоритм формулируется следующим образом:
Достоинством этого метода в том, что он постоянно пополняет результат. Поэтому поиск можно прервать при достижении достаточного количества результатов или по истечении некоторого времени.
Эта модификация своей идеей схожа с идеей Комбинаторного преобразования Хафа. Если параметры φ кривой F(φ, x) = 0 можно однозначно восстановить по К точкам, то алгоритм заполнения аккумулятора формулируется следующим образом (шаг 2):
Перед поиском следующей кривой, необходимо удалить из рассмотрения все точки предыдущих кривых, поскольку алгоритм носит случайный характер.
Анализ аккумулятора бывает часто затруднен следующими проблемами:
Причинами являются дискретизация и шум.
Для их решения можно применяются следующие методы.
Это простое решение призвано бороться с проблемами дискретизации, а именно с граничной проблемой (когда точки одно кривой могут попасть в разные ячейки аккумулятора). Для этого при заполнении аккумулятора (шаг 2), увеличивают счетчик не только той ячейки, в которую попала точка, но также увеличивают счетчики соседних ячеек.
Это тоже довольно простой метод поиска максимумов, но при этом он более устойчивый, нежели простой анализ локальных максимумов или градиентный спуск.
Суть алгоритма в том, что он оперирует не понятием значения в точке, а понятием плотности региона. Здесь плотность региона – это среднее арифметическое точек региона, то есть отношение суммы значений в каждой точке региона к количеству точек.
Пусть имеется квадратная матрица значений, размером K*K.
Поскольку сравниваемые матрицы одного размера, плотность считать не обязательно – суммы значений будет вполне достаточно. К тому же матрицы пересекаются (большей своей частью), это позволяет сильно оптимизировать алгоритм.
Рассматривается частный, наиболее простой случай применения этого метода.
Пусть дана матрица значений (например, аккумулятор). Для применения алгоритма необходимо также задать радиус окна (оно представляет собой окружность) и начальную точку – центр окна.
Существует дополнение к алгоритму, выполняющее проверку найденного максимума. После окончания основного алгоритма, окно сдвигается во всевозможных направлениях, на небольшое расстояние. Если из каждого такого положения алгоритм, опять сойдется к уже найденному максимуму, значит это стабильный максимум.
Средой разработки выбран Borland C++ Builder 6.
Реализован следующий алгоритм векторизации:
class TVectoriz
{
public:
TVectoriz();
~TVectoriz();
int toVector(int, int);
void select_PInterest(Graphics::TBitmap*, float);
unsigned int m_SizePI;
SPoint* p_PInterest;
int m_heigh, m_width;
// Вектор vElement включает в себя типы распознаваемых элементов (окружности, прямые и т. д.)
vector<TObj> vElement;
};
class IObj
{
public:
virtual void create(IObj*&) = 0;
virtual int find(SPoint*, const unsigned int&, const int&, void**) =0;
virtual void SelectFromPS(int) = 0;
// Интерфейс описывает распознаваемый элемент
virtual void draw(Graphics::TBitmap*) = 0;
};
class TLine: public IObj
{
public:
TLine(){}
~TLine(){}
void create(IObj*& aObj)
{
aObj = new TLine();
*aObj = *this;
}
int find(SPoint*, const unsigned int&, const int&, void**);
void SelectFromPS(int);
void draw(Graphics::TBitmap*){}
protected:
int find(SPoint*, const unsigned int&, const double&, const float&, int&);
// Вектор vLine хранит распознанные прямые
vector<TLineParametr> vLine;
float** pParamSpace;
int Arc, H;
float darc, dh;
};
class TArc: public IObj
{
public:
TArc(){}
~TArc(){}
void create(IObj*& aObj)
{
aObj = new TArc();
*aObj = *this;
}
int find(SPoint*, const unsigned int&, const int&, void**);
void SelectFromPS(int);
void draw(Graphics::TBitmap*);
protected:
find(SPoint* p_pi, const unsigned int& n, const int& dH, const int& R);
float** pParamSpace;
int H;
int Rtemp;
float dh;
// Вектор vArc хранит распознанные окружности
vector<TArcParametr> vArc;
};
Перед распознаванием посредством стандартного диалога "Файл открыть" указывается файл, содержащий распознаваемые образы (рис. 1).
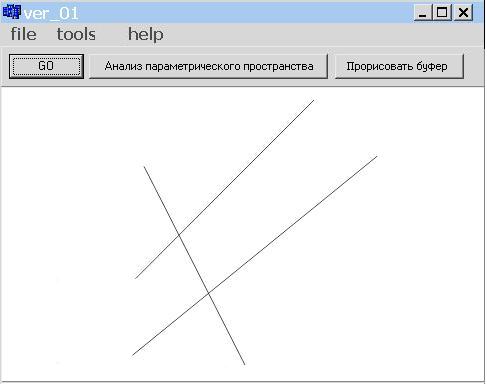
Рис. 1. Распознавание прямых
Далее необходимо выбрать тип распознаваемых образов и указать, сколько образов должно быть найдено в рисунке (рис. 2).
Рис. 2. Параметры распознавания
Также есть возможность сохранять полученное фазовое пространство в формате XMCD для дальнейшего анализа. На рис. 3 средствами MatCad показано фазовое пространство рассматриваемого примера.
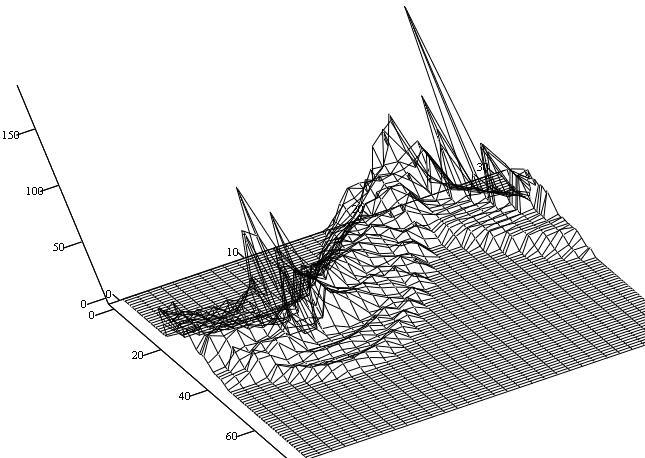
Рис. 3. Фазовое пространство, отвечающее рис. 1
В следующей версии планируется добавить
Листинг классов
void toMCAD_3dGRAF(int h, int w, float**A, TXMLDocument* xml_rez, AnsiString STR)
{
xml_rez->Active = true;
_di_IXMLNode _id_Matrix = xml_rez->DocumentElement
->ChildNodes->Nodes[(AnsiString)"regions"]
->ChildNodes->Nodes[(AnsiString)"region"]
->ChildNodes->Nodes[(AnsiString)"math"]
->ChildNodes->GetNode(0)
->ChildNodes->GetNode(1);
_id_Matrix->Attributes["rows"] = IntToStr(w);
_id_Matrix->Attributes["cols"] = IntToStr(h);
for(int i = 0; i < h; i++)
for(int j = 0; j < w; j++)
{
_di_IXMLNode temp =_id_Matrix->AddChild("ml:real");
temp->SetText(FloatToStr(A[j][i]));
}
xml_rez->SaveToFile(STR);
xml_rez->Active = false;
}
TVectoriz::TVectoriz(): m_SizePI(0), p_PInterest(NULL)
{
this->vElement.push_back();
vElement.back().p = new TLine();
this->vElement.push_back();
vElement.back().p = new TArc();
}
TVectoriz::~TVectoriz()
{
delete []p_PInterest;
}
int TVectoriz::toVector(int typeObj, int n)
{
select_PInterest(m_bmap, 1);
if(m_SizePI)
if(typeObj == 0)
{
int maska = HOUGF_TRANSFORM;
void** param = new void*[3];
param[0] = new float(0.1);
param[1] = new float(10);
param[2] = new int(sqrt(m_width * m_width + m_heigh * m_heigh));
vElement[typeObj].p->find(p_PInterest, m_SizePI, maska, param);
delete param[0];
delete param[1];
delete param[2];
delete[] param;
}
else if(typeObj == 1)
{
int maska = HOUGF_TRANSFORM;
void** param = new void*[2];
param[0] = new int(10);
param[1] = new int(47);
vElement[typeObj].p->find(p_PInterest, m_SizePI, maska, param);
delete param[0];
delete param[1];
delete[] param;
}
vElement[typeObj].p->SelectFromPS(n);
return 0;
}
void TVectoriz::select_PInterest(Graphics::TBitmap *bmap, float p
{
delete[] p_PInterest;
m_width = bmap->Width;
m_heigh = bmap->Height;
p_PInterest= new SPoint[m_width*m_heigh];
m_SizePI =0;
for (int y = 0; y < m_heigh; y++)
for (int x = 0; x < m_width; x++)
if(m_bmap->Canvas->Pixels[x][y] < clGray)
{
p_PInterest[m_SizePI].x = x;
p_PInterest[m_SizePI++].y = y;
}
}
int TLine::find(SPoint* p_pi, const unsigned int& n, const int& mask, void** param)
{
switch(mask)
{
case HOUGF_TRANSFORM:
return find(p_pi, n, *(const float *)param[0], *(const float *)param[1], *(int *)param[2]);
default:
return 0;
}
}
int TLine::find(SPoint* p_pi, const unsigned int& n, const double & dArc, const float& dH, int& Htemp)
{
darc = dArc;
dh = dH;
H = Htemp / dH;
Arc = RADIAN / dArc;
float** pParamSpace = new float*[H];
int i,j;
for(i = 0; i < H; i++)
{
pParamSpace[i] = new float[Arc];
for(j = 0; j < Arc; j++) pParamSpace[i][j] = 0;
}
float iH;
double iArc;
for(int t = 0; t < n; t++)
for(iArc = 0, j = 0; j < Arc; j++, iArc += dArc)
{
iH = fabs(p_pi[t].x * cos(iArc) + p_pi[t].y * sin(iArc));
i = (int)iH / dH;
pParamSpace[i][j]++;
}
toMCAD_3dGRAF(Arc, H, pParamSpace, Form1->xml_rez, Form1->URL_REZ);
return 0;
}
void TLine::SelectFromPS(int n)
{
vLine.clear();
while(n)
{
int H_max = 0;
int Arc_max = 0;
float temp = -1;
for(int i = 0; i < H; i++)
for(int j = 0; j < Arc; j++)
if(pParamSpace[i][j] > temp)
{
Arc_max = j;
H_max = i;
temp = pParamSpace[i][j];
}
vLine.push_back();
vLine.back().h = H_max * dh;
vLine.back().arc = Arc_max * darc;
n--;
}
for(int i = 0; i < H; i++) delete []pParamSpace[i];
delete []pParamSpace;
}
int TArc::find(SPoint* p_pi, const unsigned int& n, const int& mask, void** param)
{
switch(mask)
{
case HOUGF_TRANSFORM:
return find(p_pi, n, *(const int *)param[0], *(const int *)param[1]);
default:
return 0;
}
}
int TArc::find(SPoint* p_pi, const unsigned int& n, const int& dH, const int& R)
{
Rtemp = R;
dh = dH;
pParamSpace = new float*[H];
int i, j;
for(i = 0; i < H; i++)
{
pParamSpace[i] = new float[H];
for(j = 0; j < H; j++) pParamSpace[i][j] = 0;
}
float iX, iY;
for(int t = 0; t < n; t++)
for(iY = 0, j = 0; j < H; j++, iY += dH)
{
iX = sqrt( abs(R * R - (iY - p_pi[t].y) * (iY - p_pi[t].y))) + p_pi[t].x;
i = (int)iX / dH;
if(i < H && j < H) pParamSpace[i][j]++;
}
toMCAD_3dGRAF(H, H, pParamSpace, Form1->xml_rez, Form1->URL_REZ);
return 0;
}
void TArc::SelectFromPS(int n)
{
vArc.clear();
while(n)
{
int X_max = 0;
int Y_max = 0;
float temp = -1;
for(int i = 0; i < H; i++)
for(int j = 0; j < H; j++)
if(pParamSpace[i][j] > temp)
{
X_max = j;
Y_max = i;
temp = pParamSpace[i][j];
}
vArc.push_back();
vArc.back().R = Rtemp;
vArc.back().center.x = Y_max * dh;
vArc.back().center.y = X_max * dh;
pParamSpace[Y_max][X_max] = 0;
n--;
}
for(int i = 0; i < H; i++) delete []pParamSpace[i];
delete []pParamSpace;
}
void TArc::draw(Graphics::TBitmap* bmp)
{
int n = vArc.size();
int R;
int x0, y0;
for(int i = 0; i < n; i++)
{
R = vArc[i].R;
x0 = vArc[i].center.x;
y0 = vArc[i].center.y;
bmp->Canvas->Ellipse(x0 - R, y0 - R, x0 + R, y0 + R);
}
}