Список работ

Реализация метода Z-буфера удаления невидимых частей поверхности

Содержание

ВВЕДЕНИЕ

Известно много алгоритмов решения задачи удаления невидимых линий и поверхностей (задачи загораживания) [2].
Метод Z-буфера является одновременно и простым, и универсальным, то есть решающий любые задачи загораживания. Он реализован в известных графических приложениях. С целью ускорения счета применяются аппаратные реализации метода
Реализация метода выполнена для учебных целей. Язык программирования MAXScript. Выводимые объекты представлены полигональными моделями. Для их отображения на картинной плоскости используется прямоугольное проецирование.
При таком проецировании 3d-точка P(X, Y, Z) отобразится на плоскости проекций в виде точки с координатами x, y:

x = X; y = Y.

Изображение выводится как растровый образ заданного размера, например 200*160 пикселей, создаваемый конструктором bitmap:

btmp = bitmap 200 160 color:white.

Замечание. Рассматриваемый подход является серьезным упрощением схемы преобразований координат, применяемой в графических приложениях.

При решении задачи загораживания пиксель P0 (рис. 1) картинной плоскости, если в него проецируются несколько точек, будет закрашен цветом точки P1, имеющей наибольшую Z-координату.

Задача загораживания при параллельном проецировании

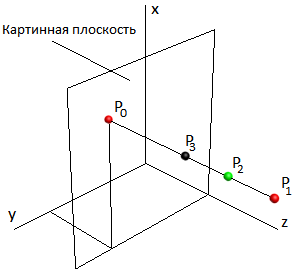
Рис. 1. Иллюстрация задачи загораживания при параллельном проецировании

Для вывода рис. 1 (без текста), можно употребить следующий код:

fn drawLine ss k p1 p2 = (
 addNewSpline ss
 addKnot ss k #corner #line p1
 addKnot ss k #corner #line p2
 updateShape ss
)
delete $*
pC = [0, 0, 0]
d = 50
d2 = d / 2
d3 = 0.75 * d
r = 1
ss = line render_renderable:off wireColor:black; drawLine ss 1 pC [-d, 0, 0]
ss = line wireColor:black; drawLine ss 1 pC [0, -d, 0]
ss = line wireColor:black; drawLine ss 1 pC [0, 0, d]
rctngl = rectangle width:50 length:50 pos:[-d2, -d2, d2] wireColor:black
rotate rctngl (eulerangles -90 0 0)
p0 = [-d3, -d2, d3]
p1 = [-d3, -1.5 * d, d3]
sphere radius:r pos:p0 wireColor:red
sphere radius:r pos:[-d3, -d, d3] wireColor:black
sphere radius:r pos:[-d3, -1.25 * d, d3] wireColor:green
sphere radius:r pos:p1 wireColor:red
ss = line wireColor:black; drawLine ss 1 p0 p1
p4 = [-d3, -d2, 0]
ss = line wireColor:black; drawLine ss 1 p0 p4
ss = line wireColor:black; drawLine ss 1 p4 [-d3, 0, 0]

МЕТОД Z-БУФЕРА

При решении задачи загораживания методом Z-буфера при выводе текущего полигона формируется его растровое представление на картинной плоскости и для каждого пикселя картинной плоскости, кроме цвета, хранится расстояние проецируемой в этот пиксель точки, вычисляемое вдоль направления проецирования.
Это расстояние хранится в двумерном массиве глубин ZB, размеры которого совпадает в размерами картинной плоскости.

Замечание. Z-буфер также называют буфером глубины.

Алгоритм Z-буфера.

  1. ZB = -∞ // Инициализировать массив глубин ZB значением -∞
  2. Для текущего пикселя p[i, j] проекции полигона определить Zp - Z-координату (глубину) точки P, принадлежащей грани и проецируемой в пиксель p[i, j].
  3. Если Zp > ZB[i, j] тогда // i, j - оконные координаты пикселя
        Закрасить пиксель p[i, j] цветом точки P     ZB[i, j] = Zp // Глубина точки P заносится в массив глубин (Z-буфер)
Код, отвечающий действиям, выполняемых для пикселя p, можно записать следующим образом:

fn treatPixel x y clrP btmp arrZ = (
 -- x, y - растровые координаты пикселя p
 -- clrP - цвет точки P, проецируемой в пиксель p
 -- btmp - растровый образ (картинная плоскость)
 -- arrZ - массив глубин
 zXY = arrZ[x][y]
 zP = findZP(x, y) -- Функция, возвращающая глубину точки P
 if zP > zXY then (
  arrZ[x][y] = zP
  setPixels btmp [x, y] #(clrP)
 )
)

ВЫЧИСЛЕНИЕ ГЛУБИНЫ

Z-координата произвольной точки P полигона, находятся по ее известным X и Y координатам, которые подставляются в уравнение плоскости, в которой лежит полигон.
Уравнение плоскости, проходящей через точку M(x0, y0, z0), перпендикулярно вектору N(A, B, C):

A(x - x0) + B(y - y0) + C(z - z0) = 0

Определим на сторонах выводимого полигона векторы e1 и e2 (рис. 2).

Вектор нормали к плоскости

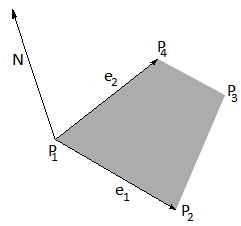
Рис. 2. Полигон и его нормаль

e1 = P2 - P1
e2 = P4 - P1

Вектор N, перпендикулярный полигону, - суть векторное произведение e1 и e2.
Для построения рис. 2 употреблен следующий код:

fn drawNGn nGn k p1 p2 p3 p4 = (
 addNewSpline nGn
 addKnot nGn k #corner #line p1
 addKnot nGn k #corner #line p2
 addKnot nGn k #corner #line p3
 addKnot nGn k #corner #line p4
 close nGn 1
 updateShape nGn
)
-- Возвращает массив ссылкой на полигон и с координатами нормали к полигону
fn dfnPlgn d ngl clr sd sM = (
 -- Затравка датчика случайных чисел
 seed sd
 -- Генерируем координаты полигона
 p1 = random [0, 0, 0] [-d, d, 0]
 p2 = random [0, 0, 0] [-d, -d, 0]
 p3 = random [0, 0, 0] [d, -d, 0]
 p4 = random [0, 0, 0] [d, d, 0]
 nGn = line render_renderable:off render_displayRenderMesh:off wireColor:clr
 drawNGn nGn 1 p1 p2 p3 p4
 convertToPoly nGn
 rotate nGn (eulerAngles ngl ngl 0)
 move nGn [sM, sM, 0]
 -- Координаты полигона после его поворота и перемещения
 p1 = nGn.verts[1].pos
 p2 = nGn.verts[2].pos
 p3 = nGn.verts[3].pos
 p4 = nGn.verts[4].pos
 -- Векторы на сторонах полигона
 e1 = p2 - p1
 e2 = p4 - p1
 -- Векторное произведение e1 и e2
 N = cross e1 e2
 return #(nGn, N)
)
delete $*
d = 40
ngl = -10
clr = [150, 150, 150]
arrNGn = dfnPlgn d ngl clr 2 0
--
-- Вывод нормали N к полигону
nrml = line render_renderable:off wireColor:black
addNewSpline nrml; addKnot nrml 1 #corner #line p1; addKnot nrml 1 #corner #line N
-- Вывод векторов e1 e2
p12 = line wireColor:black
addNewSpline p12; addKnot p12 1 #corner #line p1; addKnot p12 1 #corner #line p2
p14 = line wireColor:black
addNewSpline p14; addKnot p14 1 #corner #line p1; addKnot p14 1 #corner #line p4
--
-- Проверка
-- Z-координата точки P3 из уравнения плоскости, проходящей через P1, перпендикулярно N
nGn = arrNGn[1]
p1 = nGn.verts[1].pos
p3 = nGn.verts[3].pos
N = arrNGn[2]
z3 = p1[3] - (N[1] * (p3[1] - p1[1]) + N[2] * (p3[2] - p1[2])) / N[3]
-- Z-координата точки P3
p3[3]

Таким образом, функция, возвращающая Z-координату точки полигона, отвечающей пикселю x, y, крайне проста:

fn findZP x y M N = (
 return M[3] - (N[1] * (x - M[1]) + N[2] * (y - M[2])) / N[3]
)
-- Вызов функции
findZP p3[1] p3[2] p1 N

РЕАЛИЗАЦИЯ МЕТОДА Z-БУФЕРА

Полагается, что выводимые полигоны - это выпуклые многоугольники, закрашенные заданным цветом.
Результат отображается в виде растрового образа.
Отметим прежде, что X-координата выводимой стороны полигона при увеличении Y на 1 изменяется на угловой коэффициент k соответствующего уравнения прямой (x = k *  y + b). Поэтому очередная X-координата находится простым суммированием:

x = x + k

При выводе полигона реализуется следующая схема:

  1. Найти вершины pMi и pMa многоугольника с минимальной и максимальной Y-координатами.
  2. y = pMi[2]; xL = pMi[1]; xR = xL.
  3. Найти вершины pL и pR, смежные с pMi (pL[1] < pR[1]).
  4. Вычислить угловые коэффициенты kL и kR линий, выводимых сторон многоугольника.
  5. yE = min(pL[2], pR[2]).
  6. Если yE = pL[2] Тогда
     pE = pL
     pN = pR
    Иначе
     pE = pR
     pN = pL
    КонецЕсли.
  7. Пока y < yE Цикл
     y = y + 1
     -- Находим точки пересечения линии Y со сторонами полигона
     xL = xL + kL
     xR = xR + kR
     Для каждого пикселя x, y на отрезке [xL, xR] найти Z-координату zP точки выводимого полигона,
     проецируемой в этот пиксель и выполнить тест глубины
     и в случае его удачного завершения (zP > arrZ[x][y], где arrZ - буфер глубины)
     залить пиксель x, y заданным цветом и модифицировать arrZ: arrZ[x][y] = zP.
    КонецЦикла
    Если yE = pMa[2] Тогда
     Останов.
    КонецЕсли.
  8. Найти вершину pEN, следующую за вершиной pE.
  9. Вычислить угловой коэффициент kE линии между вершинами pE и pEN.
  10. Если pN == pL Тогда
     pR = pEN
     kR = kE
    Иначе
     pL = pEN
     kL = kE
    КонецЕсли
  11. Перейти к п. 5

Согласно схеме на каждом этапе выпуклый многоугольник заливается начиная с некоторого значения Y до ближайшей по Y вершины pE. После достижения этой вершины определяется смежная с ней вершина pEN (не пройденная), рассчитывается угловой коэффициент прямой, проходящей через pE и pEN, и выполняется следующий этап заливки, либо заливка прекращается, если все вершины пройдены.
Решение об обновлении текущего пикселя принимается по результатам теста глубины.
Оформим эту схему в виде функции fillInNGn, принимающей массив arrNGn с полигоном и его нормалью и цвет заливки.

global y, xL, xR, kL, kR, btmp, arrZ
--
-- Находит Z-координату точки полигона, проецируемой в пиксель x, y
fn findZP x y M N = (
 return M[3] - (N[1] * (x - M[1]) + N[2] * (y - M[2])) / N[3]
)
-- Помощник сортировки
fn compareFNY pA pB = (
 local d = pA[2] - pB[2]
 case of (
 (d < 0.0): -1
 (d > 0.0): 1
 default: 0
 )
)
-- Округление числа до целого значения
fn round x = (
 fx = floor x
 cx = ceil x
 return if 0.5 * (fx + cx) > x then fx else cx
)
-- Этап растровой развертки полигона
fn oneStp M N yE clr = (
 while y < yE do (
  y = y + 1
  xL += kL
  xR += kR
  xLI = round xL
  xRI = round xR
  for x = xLI to xRI do (
   -- Находим Z-координату точки полигона, проецируемой в пиксель x, y
   z = findZP x y M N
   -- Выполняем Z-тест
   if z > arrZ[y][x] do (
    -- Модифицируем и пиксель, и Z-буфер
    setPixels btmp [x, y] #(clr)
    arrZ[y][x] = z
   )
  )
 )
)
fn fillInNGn arrNGn clr = (
 local k, m, pL, pR
 nGn = arrNGn[1]
 -- Координаты вектора нормали к полигону
 N = arrNGn[2]
 nV = nGn.verts.count
 arrVs = for k = 1 to nV collect nGn.verts[k].pos
 arrVsY = copy arrVs #nomap
 qsort arrVsY compareFNY
 pMi = arrVsY[1]
 pMa = arrVsY[nV]
 y = pMi[2]; xL = pMi[1]; xR = xL
 k = findItem arrVs pMi
 pL = if k == 1 then arrVs[nV] else arrVs[k - 1]
 pR = if k == nV then arrVs[1] else arrVs[k + 1]
 if pL[1] > pR[1] do (
  pT = pL
  pL = pR
  pR = pT
 )
 kL = (xL - pL[1]) / (y - pL[2])
 kR = (xR - pR[1]) / (y - pR[2])
 for stp = 1 to nV do (
  yE = amin pL[2] pR[2]
  if yE == pL[2] then (
   pE = pL
   pN = pR
  )
  else (
   pE = pR
   pN = pL
  )
  oneStp pMi N yE clr
  if yE == pMa[2] do exit
  m = findItem arrVs pE
  pE1 = if m == 1 then arrVs[nV] else arrVs[m - 1]
  pE2 = if m == nV then arrVs[1] else arrVs[m + 1]
  pEN = if pE2[2] > pE1[2] then pE2 else pE1
  -- Угловой коэффициент kE линии между вершинами pE и pEN
  kE = (pEN[1] - pE[1]) / (pEN[2] - pE[2])
  if pN == pL then (
   pR = pEN
   kR = kE
  )
  else (
   pL = pEN
   kL = kE
  )
 )
)
-- Формирование четырехугольника
fn drawNGn nGn k p1 p2 p3 p4 = (
 addNewSpline nGn
 addKnot nGn k #corner #line p1
 addKnot nGn k #corner #line p2
 addKnot nGn k #corner #line p3
 addKnot nGn k #corner #line p4
 close nGn 1
 updateShape nGn
)
fn dfnPlgn d ngl clr sd sM = (
 -- Затравка датчика случайных чисел
 seed sd
 -- Генерируем координаты полигона
 p1 = random [0, 0, 0] [-d, d, 0]
 p2 = random [0, 0, 0] [-d, -d, 0]
 p3 = random [0, 0, 0] [d, -d, 0]
 p4 = random [0, 0, 0] [d, d, 0]
 -- Формируем четырехугольник
 nGn = line render_renderable:off render_displayRenderMesh:off wireColor:clr
 drawNGn nGn 1 p1 p2 p3 p4
 convertToPoly nGn
 rotate nGn (eulerAngles ngl ngl 0)
 move nGn [sM, sM, 0]
 -- Координаты полигона после его поворота и перемещения
 p1 = nGn.verts[1].pos
 p2 = nGn.verts[2].pos
 p3 = nGn.verts[3].pos
 p4 = nGn.verts[4].pos
 -- Векторы на сторонах полигона
 e1 = p2 - p1
 e2 = p4 - p1
 -- Векторное произведение e1 и e2
 N = cross e1 e2
 return #(nGn, N)
)
-- Основная программа (поверка процедур заливки одного полигона)
delete $*
w = 200
h = 120
-- Инициализация буфера глубины
ngtvVl = -100000.0
arrZ = for k = 1 to h collect for k2 = 1 to w collect ngtvVl
-- Создаем растровую карту белого цвета
btmp = bitmap w h color:white
-- Генерируем полигон (четырехугольник) и выполняем его поворот и сдвиг
arrNGnR = dfnPlgn 50 15 red 2 60
-- Растровая развертка многоугольника; при выводе полигон заливается красным цветом
fillInNGn arrNGnR red
-- Отображение результата (см. рис. 3)
display btmp

Заливка полигона заданным цветом

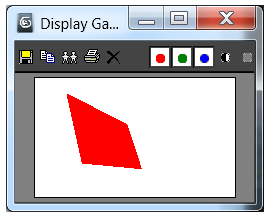
Рис. 3. Заливка полигона

-- Основная программа (поверка решения задачи загораживания)
delete $*
w = 200
h = 120
-- Инициализация буфера глубины
ngtvVl = -100000.0
arrZ = for k = 1 to h collect for k2 = 1 to w collect ngtvVl
-- Создаем растровую карту белого цвета
btmp = bitmap w h color:white
-- Генерируем три пересекающихся четырехугольника и выполняем их поворот и сдвиг
sR = 50; sG = 60; sB = 40
sM = amax #(sR, sG, sB)
arrNGnR = dfnPlgn sR 15 red 2 sM
arrNGnG = dfnPlgn sG 0 green 3 sM
arrNGnB = dfnPlgn sB 15 blue 4 sM
-- Растровая развертка многоугольников с учетом загораживания (см. рис. 4)
fillInNGn arrNGnR red
fillInNGn arrNGnG green
fillInNGn arrNGnB blue
-- Отображение результата
display btmp

Z-буфер: вывод пересекающихся многоугольников

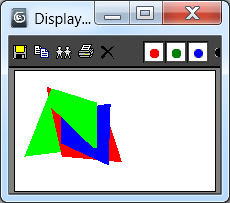
Рис. 4. Вывод трех пересекающихся полигонов

ЗАКЛЮЧЕНИЕ

В случае центрального проецирования несколько усложняется расчет Z-координат проецируемых точек полигона, но суть метода не меняется.
Случай вывода невыпуклой фигуры (полигона) оставляется студентам для самостоятельной проработки.
Порядок вывода растровой развертки иллюстрирует рис. 5.

Обработка линии Y при развертке невыпуклой фигуры

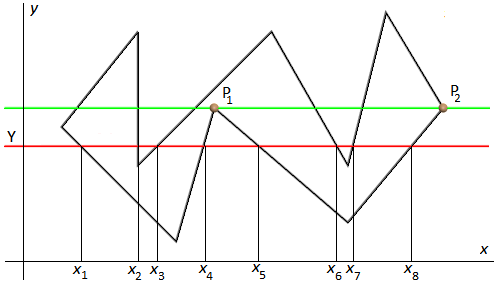
Рис. 5. Растровая развертка невыпуклого многоугольника

Согласно рис. 5. на каждой линии Y нужно выполнить следующие действия:

  1. Найти точки пересечения линии Y со сторонами многоугольника.
  2. Упорядочить найденные точки по возрастанию Х-координат.
  3. Залить заданным (или рассчитанным) цветом пиксели линии Y на отрезках [x1, x2], [x3, x4] и т. д., пропуская отрезки [x2, x3], [x4, x5] и т. д.

Если линия Y пересекает в одной точке две стороны многоугольника (см. зеленую линию на рис. 5 и точки P1 и P2), то нумеруется только точка пересечения с стороной многоугольника в ее верхней вершине. Так, в P1 в список точек пересечения зеленой линии Y со сторонами многоугольника будут добавлены 2 точки, а в P2 - одна.

Вывод приведенного на рис. 5 многоугольника (без надписей) обеспечивает следующий код:

fn drwN2 p1 p2 clr = (
n2 = line wireColor:clr
addNewSpline n2
addKnot n2 1 #corner #line p1
addKnot n2 1 #corner #line p2
updateShape n2
)
delete $*
-- Многоугольник
nGn = line wireColor:black
addNewSpline nGn
addKnot nGn 1 #corner #line [-120, 0, 0]
addKnot nGn 1 #corner #line [-60, -60, 0]
addKnot nGn 1 #corner #line [-40, 10, 0]
addKnot nGn 1 #corner #line [30, -50, 0]
addKnot nGn 1 #corner #line [80, 10, 0]
addKnot nGn 1 #corner #line [50, 60, 0]
addKnot nGn 1 #corner #line [30, -20, 0]
addKnot nGn 1 #corner #line [-10, 50, 0]
addKnot nGn 1 #corner #line [-80, -20, 0]
addKnot nGn 1 #corner #line [-80, 50, 0]
addKnot nGn 1 #corner #line [-80, 50, 0]
close nGn 1
updateShape nGn
-- Красная и зеленая линии Y
drwN2 [-150, -10, 0] [120, -10, 0] red
drwN2 [-150, 10, 0] [120, 10, 0] green
-- Оси координат
drwN2 [-140, 70, 0] [-140, -80, 0] black
drwN2 [-150, -70, 0] [120, -70, 0] black
-- Х-координаты точек пересечения красной линии Y со сторонами полигона
drwN2 [-110, -10, 0] [-110, -70, 0] black
drwN2 [-80, -10, 0] [-80, -70, 0] black
drwN2 [-70, -10, 0] [-70, -70, 0] black
drwN2 [-45, -10, 0] [-45, -70, 0] black
drwN2 [-17, -10, 0] [-17, -70, 0] black
drwN2 [24, -10, 0] [24, -70, 0] black
drwN2 [33, -10, 0] [33, -70, 0] black
drwN2 [63, -10, 0] [63, -70, 0] black
sphere radius:2.5 pos:[-40, 10, 0] wireColor:brown
sphere radius:2.5 pos:[80, 10, 0] wireColor:brown

ЛИТЕРАТУРА

  1. Autodesk® 3ds Max® 2009 MAXScript Reference.
  2. Шикин Е. В., Боресков А. В. Компьютерная графика. Динамика, реалистические изображения. - М.: Диалог-МИФИ, 1995. - 288 с.

Список работ

Рейтинг@Mail.ru