Рассматривается модель пловца, выполненная на базе Biped (двуногого). Модель реализована средствами языка MAXScript.
Анимация Biped может быть выполнена интерактивно, например, в режиме Footstep или в результате задания ключей анимации, которые могут быть созданы для выбранного элемента Biped на вкладке Motion, в окне Workbench или Curve Editor.
Кнопочное (ручное) задание ключей анимации Biped, отражающей, например, упражнения Тай-Чи или иные нетривиальные движения, – это весьма трудоемкая задача. Однако, работая в 3ds Max, решение такой задачи можно автоматизировать, применяя MAXScript. На входе MAXScript-программы могут быть данные, полученные в результате захвата движений, либо импортированные из других приложений, либо рассчитанные с помощью соответствующей математической модели.
В настоящем примере иллюстрируется последний подход формирования входных данных.
Интерактивные средства управления Biped не рассматриваются.
Запуск программы выполняется в 3ds Max в следующем порядке:
Объекты 3ds Max имеют свойства, значения которых могут изменяться во времени. Например, можно изменять радиус сферы или ее позицию.
Зависимость изменения значения свойства во времени называется анимационной кривой.
На рис. 1 приведен пример анимационной кривой. Порядок ее формирования рассмотрен чуть ниже.
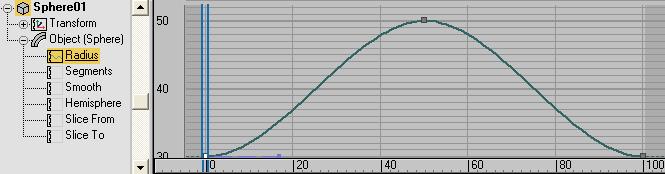
Рис. 1. Анимационная кривая радиуса сферы
Контроллер 3ds Max – это, как правило, объект, содержащий данные, используемые для построения анимационной кривой.
Классификация контроллеров 3ds Max – это отдельная тема, здесь же приведем вводные сведения, в определенной мере способствующие восприятию настоящего материала.
Контроллеры разделяются на преопределенные и назначаемые.
Предопределенными контроллерами объект обладает с момента его создания. Так, после создания сфера, а точнее ее свойство Position, обладает контроллером Position_XYZ. В этом можно убедиться, выполнив в MAXScript Editor нижеприводимый код и просмотрев результаты в MAXScript Listener:
delete $*
animationRange = interval 0f 100f
sph = sphere radius:30
cP = sph.Position.Controller -- Controller:Position_XYZ
showProperties cP
--.X_Position : float
--.Y_Position : float
-- .Z_Position : float
В приведенном коде сфера создается конструктором Sphere.
Выражение sph.Position.Controller возвращает ссылку на контроллер свойства Position сферы.
Метод ShowProperties показывает свойства объекта, ссылка на который передана методу в качестве параметра (в данном случае – это ссылка cP). Метод вернет false, если ему подать неподходящий параметр.
Метод Delete $* очищает сцену; метод будет присутствовать практически в каждом примере кода.
В примерах этого раздела используется анимационный интервал длиной в 100 кадров, устанавливаемый путем задания значения системной глобальной переменной animationRange.
Свойство Radius после создания сферы контроллером не обладает, что подтверждает следующий код, печатающий для выражения sph.Radius.Controller значение undefined (не пределен):
delete $*
sph = sphere radius:30
sph.Radius.Controller -- undefined
Анимация свойства, не обладающего изначально контроллером, может быть выполнена методом Animate On, например:
delete $*
sph = sphere()
animate on (
at time 0 sph.Radius = 30
at time 50 sph.Radius = 50
at time 100 sph.Radius = 30
)
sph.Radius.Controller -- Controller:Bezier_Float
playAnimation()
Метод PlayAnimation воспроизводит анимацию сцены.
Отметим, что в результате выполнения метода Animate On свойству Radius сферы будет назначен контроллер Bezier_Float, на что в приведенном коде укажет выражение sph.Radius.Controller. Анимационная кривая радиуса показана на ранее приведенном рис. 1. Для ее наблюдения следует выполнить: меню Graph Editors – Track View – Curve Editor – ветвь Objects – Sphere01 – Object – Radius.
Анимацию свойства, имеющего предопределенный контроллер, также можно осуществить методом Animate On, например:
delete $*
sph = sphere radius:30
animate on (
at time 0 sph.Pos = [0, 40, 0]
at time 50 sph.Pos = [0, -50, 0]
at time 100 sph.Pos = [0, 40, 0]
)
playAnimation()
Можно, однако, прибегнуть к явному заданию ключей анимации, например:
delete $*
sph = sphere radius:30
cP = sph.Position.Controller -- Controller:Position_XYZ
cPY = cP.Y_Position.Controller
addNewKey cPY 0 -- #Bezier Float key(1 @ 0f)
addNewKey cPY 50 -- #Bezier Float key(2 @ 50f)
addNewKey cPY 100 -- #Bezier Float key(3 @ 100f)
ks = cPY.Keys -- #keys(0f, 50f, 100f)
ks[1].Value = 40
ks[2].Value = -50
ks[3].Value = 40
playAnimation()
В коде учтена особенность контроллера Position_XYZ: он является составным и осуществляет раздельное управление своими компонентами X_Position, Y_Position и Z_Position посредством трех контроллеров Bezier_Float. Эти три контроллеры также являются предопределенными.
Имя контроллера указывает на вид формируемой по его данным анимационной кривой (сплайн Безье) и на тип возвращаемых им данных (Float, вещественные данные).
В приведенном коде для сокращения вводится ссылка cPY на контроллер sph.Position.Controller.Y_Position.Controller.
Далее методом addNewKey формируются 3 ключа анимации в точках 0, 50 и 100 временного интервала (время указывается в кадрах).
Свойство Keys принадлежит классу MAXKeyArray и содержит массив ключей контроллера.
Значение свойства Y_Position родительского контроллера Position_XYZ устанавливается путем изменения свойства Value соответствующего ключа.
Контроллеры также можно поделить на контроллеры, обладающие ключами и контроллеры, не имеющие таковых.
Так, контроллер Bezier_Float функционирует на основе анимационных ключей, а рассмотренный в работе "Параметрическая модель стула" контроллер Float_Expression формирует анимационную кривую по указанному в нем выражению. Это подтверждает следующий пример:
delete $*
animationRange = interval 0f 100f
sph = sphere()
fltX = float_expression()
fltX.SetExpression "if(F < 50, F, 100 - F)"
sph.Radius.Controller = fltX
fltX.Keys -- #keys()
playAnimation()
В примере контроллер Float_Expression возвращает вещественно число, линейно зависящее от текущего времени. Радиус сферы устанавливается равным этому числу. Параметр F использованного выражения – это текущее, измеряемое в кадрах время анимации. Согласно выражению, радиус сферы равен F, если время меньше половины длины анимационного интервала, в противном случае радиус равен 100 – F. Сформированная контроллером анимационная кривая радиуса показана на рис. 2.
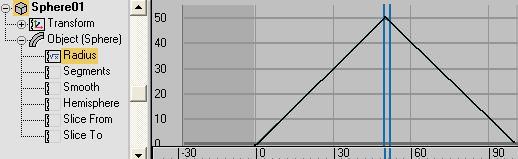
Рис. 2. Анимационная кривая радиуса, сформированная контроллером Float_Expression
При формировании модели пловца используются только предопределенные, обладающие ключами контролеры.
В случае таких контроллеров их программирование заключается в создании ключей анимации и в определении значений свойств созданных ключей.
Структура используемого Biped и отвечающей этой структуре двуногий приведены на рис. 3.
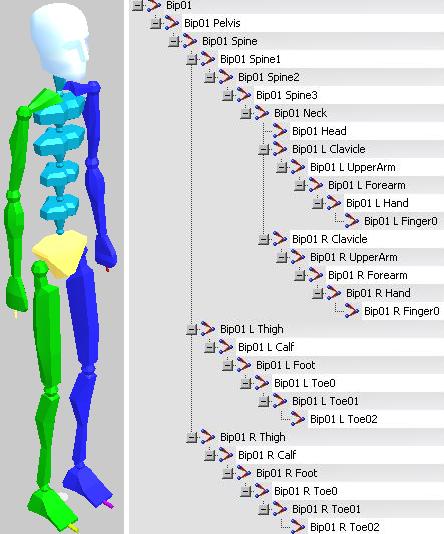
Рис. 3. Используемый Biped и его структура
Такой Biped создается следующим конструктором:
b2 = biped.CreateNew 100 -90.0 [0, 0, 0]
Первый параметр конструктора – это высота двуногого, второй – ориентация объекта (при нулевом значении этого параметра взгляд Biped устремлен в положительном направлении оси Х), а третий – позиция центра массы объекта. Угол поворота Biped и позиция центра массы задаются в мировой системе координат.
Компоненты двуногого, структура которого приведена на рис. 3, имеют номера и имена, используемые MAXScript для получения ссылки на компонент. Эти сведения приведены в следующей таблице:
| Индекс | Имя | Компонент Biped и подчиненные ему компоненты | |||
|---|---|---|---|---|---|
| 1 | #larm | L Clavicle | L UpperArm | L Forearm | L Hand |
| 2 | #rarm | R Clavicle | R UpperArm | R Forearm | R Hand |
| 5 | #lleg | L Thigh | L Calf | L Foot | |
| 6 | #rleg | R Thigh | R Calf | R Foot | |
| 9 | #spine | Spine | Spine1 | Spine2 | Spine3 |
| 11 | #head | Head | |||
| 12 | #pelvis | Pelvis | |||
| 17 | #neck | Neck | |||
Ссылку на компонент Biped вернет метод biped.GetNode:
nd = biped.GetNode <biped> <index> [link:<int_link>]
Первый параметр метода – это ссылка на Biped, второй – это номер корневого компонента рассматриваемой части тела (берется из столбца Индекс), третий, необязательный, – это номер дочернего компонента в иерархии рассматриваемой части тела.
Используя вышеприведенную таблицу, получим, например, ссылки на левую ладонь двуногого, его правую ступню и голову:
delete $*
b2 = biped.CreateNew 100 0.0 [0, 0, 0]
ndL = biped.GetNode b2 1 link:4 -- L Hand
ndFR = biped.GetNode b2 6 link:3 -- R Foot
ndH = biped.GetNode b2 11 -- Head
При этом свойство Parent (родитель) компонентов ndL и ndFR будет соответственно иметь значение L Forearm и R Calf:
ndL.Parent -- L Forearm
ndFR.Parent -- R Calf
Приводятся сведения, необходимые для реализации разбираемой ниже модели пловца.
Biped, взятый как единое целое, управляется так называемым Body-контроллером, позволяющим изменять координаты тела двуногого в мировой системе координат. Контролер создается конструктором Transform.Controller или Controller, например:
b2 = biped.CreateNew 100 -90.0 [0, 0, 0]
bc = b2.Transform.Controller -- bc = b2.Controller
Далее используется короткая форма конструктора.
Body-контроллер принадлежит классу Vertical_Horizontal_Turn. Контролер обеспечивает доступ к компонентам Vertical, Horizontal и Turning класса SubAnim, посредством которых можно перемещать и вращать Biped. Эти операции выполняются средствами соответствующих контроллеров.
Пример. Анимировать перемещение Biped по оси Y на 100 единиц и его поворот относительно оси X на 360°.
delete $*
animationRange = interval 0f 100f
b2 = biped.CreateNew 100 0.0 [0, 0, 0]
b2.Pivot = [0, 0, 0]
bc = b2.Controller
bcH = bc.Horizontal.Controller
bcT = bc.Turning.Controller
with redraw off (
ks = biped.AddNewKey bcH 0
ks.Y = 50
ks = biped.AddNewKey bcH 100
ks.Y = -50
ks = biped.AddNewKey bcT 0
ks.Rotation = eulerAngles 0 0 0 as quat
ks = biped.AddNewKey bcT 50
ks.Rotation = eulerAngles 180 0 0 as quat
ks = biped.AddNewKey bcT 100
ks.Rotation = eulerAngles 360 0 0 as quat
sliderTime = 0f
)
playAnimation()
Два кадра анимации приведены на рис. 4.

Рис. 4. 35-й и 70-й кадры анимации Biped
В приведенном решении присваивание b2.Pivot = [0, 0, 0] вызывает перемещение базовой точки Biped в начало мировой системы координат. Наличие конструкции With Redraw с параметром off обеспечивает задание ключей анимации без перерисовки сцены.
Контроллер bcH = bc.Horizontal.Controller обеспечивает управление X и Y координатами Biped, а контроллер bcT = bc.Turning.Controller управляет поворотом двуногого.
Анимационные ключи создаются методом biped.AddNewKey. В случае контроллера bcH ключ имеет свойства X и Y, а в случае bcT – свойство Rotation. Единица измерения Rotation – кватернион.
Управление Z координатой двуногого выполняется посредством Vertical-контроллера, например код:
delete $*
b2 = biped.CreateNew 100 0.0 [0, 0, 0]
bc = b2.Controller
bcV = bc.Vertical.Controller
ks = biped.AddNewKey bcV 0
ks.Z = -25
ks = biped.AddNewKey bcV 100
ks.Z = 25
sliderTime = 0f
playAnimation()
обеспечит анимацию перемещения Biped по оси Z.
Заметим, что ключи, создаваемые в приводимых примерах, имеют и иные свойства, знакомство с которыми выходит за границы настоящего материала.
Координаты компонента Biped могут быть изменены после ассоциирования компонента с подходящим контроллером, например Bezier_Position. Также можно употребить метод biped.SetTransform, выполняющий преобразование перемещения, поворота или масштабирования отдельного компонента Biped и при необходимости создающий ключ в текущей точке временного интервала контроллера компонента. Например:
sliderTime = 20f
biped.SetTransform nd #pos [20, 30, 0] true
Первым параметром метода является ссылка на компонент Biped, вторым – вид преобразования #pos, #rotation или #scale, третьим – значение ключа, а четвертым – флаг создания ключа. Ключ будет создан, если этот флаг имеет значение true. В противном случае преобразование будет выполнено без создания ключа.
Пример. Приподнять правую руку Biped на 30 единиц по оси Z и удалить ее от плеча на 10 единиц по оси X.
delete $*
b2 = biped.CreateNew 100 0.0 [0, 0, 0]
ndR = biped.GetNode b2 2 link:4 -- R Hand
btp = biped.GetTransform ndR #pos
biped.SetTransform ndR #pos (btp + [10, 0, 30]) false
btp2 = biped.GetTransform ndR #pos
Координаты компонента Biped (в данном случае ладони правой руки) возвращаются методом biped.GetTransform. До преобразования они равны [0.0142776,-10.6849,-41.681], а после преобразования имеют значение [10.0143,-10.6849,-11.681]. Используется мировая система координат.
Если же попытаться приподнять ладонь на 300 единиц, то, несмотря на бессмысленность такой попытки (величина смещения существенно превосходит длину руки), преобразование все же будет выполнено, а результирующие координаты ладони окажутся равными [1.0656,-8.13174,15.8423].
Иными словами, плохие позиции буду восприняты методом, но нередко с непредсказуемым результатом.
Результаты описанных преобразований приведены на рис. 5.
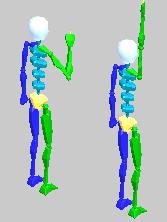
Рис. 5. Преобразования позиции правой ладони Biped
Аналогичный результат можно получить, назначив компоненту R Hand контроллер Bezier_Position, например:
delete $*
b2 = biped.CreateNew 100 0.0 [0, 0, 0]
bc = b2.Controller
ndR = biped.GetNode b2 2 link:4 -- R Hand
bzP = bezier_position()
biped.CreatePosSubAnims bc bzP true
biped.SetPosSubAnim bc [0, 0, 0] ndR true
biped.SetPosSubAnim bc [10.0143,-10.6849,-11.681] ndR true
Рассмотрение назначаемых контроллеров Biped выходит за рамки настоящего материала. Далее будет употребляться только метод biped.SetTransform.
Чтобы не задавать бессмысленные значения координат, достаточно знать векторы масштабирования компонентов объекта. Эти значения для указанного элемента можно получить методом biped.GetTransform с параметром #scale.
Пример. Определяется вектор масштабирования левого предплечья двуногого, высота которого равна 100 единицам.
delete $*
b2 = biped.CreateNew 100 0.0 [0, 0, 0]
ndL = biped.GetNode b2 1 link:2 -- L UpperArm
bts = biped.GetTransform ndL #scale -- [14.4578,14.4578,14.4578]
Изменение высоты объекта приведет к пропорциональному изменению векторов масштабирования его компонентов.
В основном примере рассматривается модель пловца, использующего стиль плавания "Ми-8": быстрая работа рук подобна вращению лопастей вертолета.
Стиль напоминает кроль, не столь эффективен, но весьма выразителен (рис. 6).
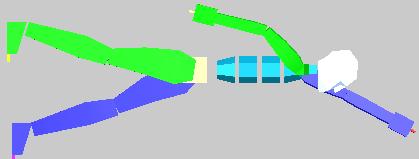
Рис. 6. Стиль плавания Ми-8 (фрагмент)
Изначально пловец помещается в начало координат. Движение выполняется в отрицательном направлении оси Y.
Особенности стиля Ми-8:
Центр окружности, задающей траекторию движения ладони пловца, размещен в базовой точке соответствующего предплечья. Центр окружности, задающей траекторию движения ступни пловца, размещен в базовой точке соответствующего бедра.
Замеры Biped показывают, что базовая точка правого предплечья находится в позиции
[-0.0801 * H, 0, 0.30825 * H],
где H – высота Biped, а сам Biped помещен в начало координат. В позицию правого предплечья помещен центр окружности, задающей траекторию движения правой ладони. Центр окружности для ладони левой руки находится в позиции
[0.0801 * H, 0, 0.30825 * H].
Длина руки, вычисляемая как расстояние между базовыми точками предплечья и ладони Biped, равна
(0.30825 – 0.01988) * H = 0.28837 * H.
Это значение используется в качестве радиуса окружностей для ладоней пловца.
Позиция базовой точки правого бедра равна
[-0.04854 * H, 0, 0].
В эту позицию помещен центр окружности, задающей траекторию движения правой ступни. Центр окружности для ступни левой ноги находится в точке
[0.04854 * H, 0, 0].
Длина ноги, вычисляемая как расстояние между базовыми точками бедра и ступни Biped, равна
0.48301* H.
Это значение используется в качестве радиуса окружностей для ступней ног пловца.
Тогда имеем следующее уравнение окружности, задающей траекторию правой ладони:
y = 0.28837 * cosφ* H
z = (0.30825 + 0.28837 * sinφ) * H
φ ∈ [0, 360]
Уравнение окружности, определяющей траекторию правой ступни:
y = 0.48301 * cosφ * H
z = 0.48301 * sinφ * H
φ ∈ [-110, -60]
Очевидны уравнения и левых окружностей рассматриваемых частей тела Biped.
На рис. 7 показаны посредством сфер траектории движения рук и ног двуногого.
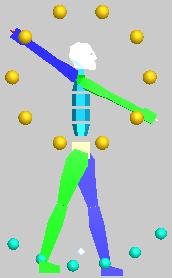
Рис. 7. Стиль Ми-8: траектории движения ладоней и ступней
Для формирования рис. 7 использован следующий код (для наглядности несколько увеличена длина траектории ступней ног):
delete $*
h = 100
b2 = biped.CreateNew h -90.0 [0, 0, 0]
b2.Pivot = [0, 0, 0]
d = 36
ng = -d
x = -0.1 * h
for k = 1 to 10 do (
ng += d
y = 0.28837 * cos ng * h
z = (0.30825 + 0.28837 * sin ng) * h
sphere radius:3 pos:[x, y, z] wireColor:[135, 110, 8]
)
d = 16
ng = -150
x = -0.04854 * h
for k = 1 to 6 do (
ng += d
y = 0.48301 * cos ng * h
z = 0.48301 * sin ng * h
sphere radius:2.5 pos:[x, y, z] wireColor:[6, 135, 113]
)
Движение пловца показывается на интервале из 216 кадров. За это время руки выполняют 3 оборота по 360°. Угловая скорость ног в 3 раза превышает угловую скорость рук, поэтому каждая нога выполняет по 9 циклических движений. Угловые движения головы и позвоночника выполняются с одинаковой периодичностью.
Обсудим теперь программу, позволяющую Biped плыть стилем Ми-8. В программе функции Hand, Foot, Head и Spine отвечают за движение отдельных частей тела пловца. Функция MvLL управляет пловцом, как единым целым. Используемые в расчетных формулах коэффициенты округлены до 2-го десятичного знака, что не влияет на качество анимации.
Функция Hand вызывается дважды. При первом обращении она создает ключи анимации элемента L Hand, а при втором – R Hand.
fn hand nd d ngs x dt ni nj h = (
tm = -dt
sc = 0.29; z0 = 0.31
for j = 1 to nj do (
ng = ngs - d
for k = 1 to ni do (
ng += d
y = sc * cos ng * h
z = (z0 + sc * sin ng) * h
tm += dt
sliderTime = tm
biped.SetTransform nd #pos [x, y, z] true
)
)
)
Функция Foot создает ключи анимации элементов L Foot и R Foot.
fn foot b2 x dt ni nj kj h = (
d = 8
tm = -dt
sc = 0.48
ng = -118
ng2 = -68
ni2 = 0.5 * ni + 1
ndFL = biped.GetNode b2 5 link:3 -- L Foot
ndFR = biped.GetNode b2 6 link:3 -- R Foot
for j = 1 to (nj * kj) do (
for k = 1 to ni do (
d2 = if k < ni2 then d else -d
ng += d2
ng2 -= d2
y = sc * cos ng * h
z = sc * sin ng * h
y2 = sc * cos ng2 * h
z2 = sc * sin ng2 * h
tm += dt
sliderTime = tm
biped.SetTransform ndFL #pos [x, y, z] true
biped.SetTransform ndFR #pos [-x, y2, z2] true
)
)
)
Функция Head отвечает за покачивание головой (элемент Head, рис. 8).
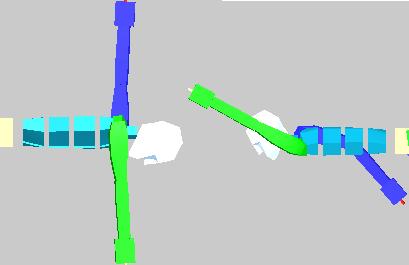
Рис. 8. Предельные положения головы пловца
fn head b2 tSp nj = (
dt = (2.0 / 3.0) * tSp
tm = -dt
ndH = biped.GetNode b2 11 -- Head
arrBtr = #(eulerAngles -90 -70 -90, eulerAngles 90 -60 90)
for j = 1 to nj do
for k = 1 to 2 do (
tm += dt
sliderTime = tm
biped.SetTransform ndH #rotation (arrBtr[k] as quat) true
)
)
Функция Spine, воздействуя на одноименный элемент Spine, управляет угловыми движениями тела относительно вектора скорости (рис. 9).

Рис. 9. Предельные повороты корпуса пловца (вид сверху)
fn spine b2 ngS tSp nj = (
dt = (2.0 / 3.0) * tSp
tm = -dt
dNg = 2 * (-90 - ngS)
ndSpn = biped.GetNode b2 9 link:1 -- Spine
for j = 1 to nj do (
ng = ngS
for k = 1 to 2 do (
tm += dt
sliderTime = tm
btr = eulerAngles -90 -90 ng as quat
biped.SetTransform ndSpn #rotation btr true
ng += dNg
)
)
)
Функция MvLL ориентирует Biped вдоль оси Y и организует его перемещение в отрицательном направлении этой оси.
fn mvLL bc aRng = (
bcT = bc.Turning.Controller
ks = biped.AddNewKey bcT 0f
ks.Rotation = quat -0.5 -0.5 0.5 0.5
ks = biped.AddNewKey bcT aRng
ks.Rotation = quat -0.5 -0.5 0.5 0.5
--
bcH = bc.Horizontal.Controller
ks = biped.AddNewKey bcH 0f
ks.Y = 70
ks = biped.AddNewKey bcH aRng
ks.Y = -70
)
Вспомогательная функция Prps выполняет подготовку сцены.
Ниже приводится вся программа, которую можно скопировать и исполнить в MAXScript Editor, а далее следуют несколько кадров анимации (рис. 10).
fn prps = (
delete $*
units.DisplayType = #Generic
units.SystemType = #Inches
viewport.SetLayout #layout_4
viewport.ActiveViewport = 4
max vpt persp user
viewport.SetGridVisibility 4 false
)
fn hand nd d ngs x dt ni nj h = (
tm = -dt
sc = 0.29; z0 = 0.31
for j = 1 to nj do (
ng = ngs - d
for k = 1 to ni do (
ng += d
y = sc * cos ng * h
z = (z0 + sc * sin ng) * h
tm += dt
sliderTime = tm
biped.SetTransform nd #pos [x, y, z] true
)
)
)
fn foot b2 x dt ni nj kj h = (
d = 8
tm = -dt
sc = 0.48
ng = -118
ng2 = -68
ni2 = 0.5 * ni + 1
ndFL = biped.GetNode b2 5 link:3 -- L Foot
ndFR = biped.GetNode b2 6 link:3 -- R Foot
for j = 1 to (nj * kj) do (
for k = 1 to ni do (
d2 = if k < ni2 then d else -d
ng += d2
ng2 -= d2
y = sc * cos ng * h
z = sc * sin ng * h
y2 = sc * cos ng2 * h
z2 = sc * sin ng2 * h
tm += dt
sliderTime = tm
biped.SetTransform ndFL #pos [x, y, z] true
biped.SetTransform ndFR #pos [-x, y2, z2] true
)
)
)
fn head b2 tSp nj = (
dt = (2.0 / 3.0) * tSp
tm = -dt
ndH = biped.GetNode b2 11 -- Head
arrBtr = #(eulerAngles -90 -70 -90, eulerAngles 90 -60 90)
for j = 1 to nj do
for k = 1 to 2 do (
tm += dt
sliderTime = tm
biped.SetTransform ndH #rotation (arrBtr[k] as quat) true
)
)
fn spine b2 ngS tSp nj = (
dt = (2.0 / 3.0) * tSp
tm = -dt
dNg = 2 * (-90 - ngS)
ndSpn = biped.GetNode b2 9 link:1 -- Spine
for j = 1 to nj do (
ng = ngS
for k = 1 to 2 do (
tm += dt
sliderTime = tm
btr = eulerAngles -90 -90 ng as quat
biped.SetTransform ndSpn #rotation btr true
ng += dNg
)
)
)
fn mvLL bc aRng = (
bcT = bc.Turning.Controller
ks = biped.AddNewKey bcT 0f
ks.Rotation = quat -0.5 -0.5 0.5 0.5
ks = biped.AddNewKey bcT aRng
ks.Rotation = quat -0.5 -0.5 0.5 0.5
--
bcH = bc.Horizontal.Controller
ks = biped.AddNewKey bcH 0f
ks.Y = 70
ks = biped.AddNewKey bcH aRng
ks.Y = -70
)
prps()
ni = 12
nj = 3
-- Time space
tSp = 72.0
aRng = nj * tSp
animationRange = interval 0f aRng
with redraw off (
h = 100.0
b2 = biped.CreateNew h -90.0 [0, 0, 0]
bc = b2.Controller
bc.BodyType = 3 -- Classic
b2.Pivot = [0, 0, 0]
d = 30
x = 0.08 * h
dt = tSp / ni
ndL = biped.GetNode b2 1 link:4 -- L Hand
ndR = biped.GetNode b2 2 link:4 -- R Hand
-- Hands
hand ndL d 0 x dt ni nj h
hand ndR d 180 -x dt ni nj h
x2 = 0.05 * h
kj = 3
dt2 = dt / kj
-- Foot
foot b2 x2 dt2 ni nj kj h
-- Head
head b2 tSp nj
-- Spine
spine b2 -110 tSp nj
-- Move
mvLL bc aRng
sliderTime = 0f
)
playAnimation()

Рис. 10. Ми-8
Используя описанные средства, можно реализовать модели различных регулярных движений, выполняемых, например, лыжниками или конькобежцами. Нерегулярные движения с большим числом оттенков, скажем, движения балерины, также можно представить в виде Biped-моделей, но с привлечением иных методов, основанных, например, на захвате движений.