Система итерируемых функций (СИФ, Iterated functions system) – это средство получения фрактальных структур.
Наиболее простая СИФ состоит из аффинных преобразований на плоскости. (Напомним, что аффинные преобразования координат – это в общем случае суперпозиция масштабирования, поворота, параллельного переноса и зеркального отображения.)
В общей виде аффинное преобразование на плоскости задается следующей системой уравнений:
X' = A * X + B * Y + E
Y' = C * X + D * Y + F
Число систем уравнений, используемых для получения фрактальной структуры, не менее двух. Так для получения фрактальной решетки (Lattice, рис. 1) берутся следующие четыре системы:
(1, вероятность выбора 0.25)
X' = 0.3 * X - 0.3 * Y + 1
Y' = 0.3 * X + 0.3 * Y + 1
(2, вероятность выбора 0.25)
X' = 0.3 * X - 0.3 * Y + 1
Y' = 0.3 * X + 0.3 * Y - 1
(3, вероятность выбора 0.25)
X' = 0.3 * X - 0.3 * Y - 1
Y' = 0.3 * X + 0.3 * Y + 1
(4, вероятность выбора 0.25)
X' = 0.3 * X - 0.3 * Y - 1
Y' = 0.3 * X + 0.3 * Y - 1
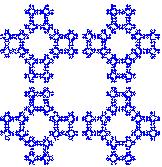
Рис. 1. Фрактальная решетка (построена как растровый образ)
Каждая система называется СИФ-преобразованием.
В СИФ применяются сжимающиеся аффинные преобразования, то есть такие, в которых коэффициент масштабирования меньше единицы.
Алгоритм построения СИФ-фрактала:
В качестве начальной можно брать любую принадлежащую изображению точку. Приводимый ниже алгоритм поиска начальной точки обеспечивает ее выбор в так называемом аттракторе, то есть в области, принадлежащей изображению фрактала. Все последующие точки, найденные по вышеприведенному алгоритму построения СИФ-фрактала, блуждают в области аттрактора, не перемещаясь в области, не принадлежащие изображению.
Алгоритм поиска начальной точки:
Рассматривая каждое СИФ-преобразование в отдельности, можно заметить, что независимо от положения начальной точки после нескольких итераций точка перестает двигаться. Точка остановки называется неподвижной точкой.
Неподвижная точка каждого преобразования входит в состав аттрактора. Поэтому за начальную точку при построении фрактала можно взять неподвижную точку, например, первого преобразования.
СИФ можно представить более компактно в виде следующей таблицы:
| A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|
| 0.3 | -0.3 | 0.3 | 0.3 | 1 | 1 | 0.25 |
| 0.3 | -0.3 | 0.3 | 0.3 | 1 | -1 | 0.25 |
| 0.3 | -0.3 | 0.3 | 0.3 | -1 | 1 | 0.25 |
| 0.3 | -0.3 | 0.3 | 0.3 | -1 | -1 | 0.25 |
В последнем столбце для каждого СИФ-преобразования указывается вероятность его выбора при поиске очередной точки изображения фрактала.
В примере эти вероятности равны, что, впрочем, не характерно.
Приводимый ниже код обеспечивает вывод показанной на рис. 1 фрактальной решетки.
global ifs, xP, yP, ifsCnt
global xI, yI, xA, yA
-- Вычисляет координаты очередной точки изображения фрактала
-- Параметры x и y передаются по ссылке
fn affine col &x &y = (
t = x * col[1] + y * col[2] + col[5]
y = x * col[3] + y * col[4] + col[6]
x = t
)
-- Находит начальную точку изображения
fn sPoint = (
-- Берем первое СИФ-преобразование
col = for k = 1 to 6 collect ifs[k]
-- После 100 итераций xP и yP – это координаты начальной точки
for k = 1 to 100 do affine col &xP &yP
)
-- Выбирает, используя датчик случайных чисел и вероятности выбора,
-- СИФ-преобразование для вычисления координат очередной точки изображения
fn findK12 &k11 &k22 = (
-- Получаем случайное число из диапазона 0.0 – 1.0
r = random 0.0 1.0
p = 0.0
-- j2 – число строк в таблице СИФ-преобразований
j2 = ifsCnt / 7
j3 = j2 - 1
for j = 1 to j3 do (
p += ifs[7 * j]
if r <= p then (j2 = j; exit)
)
-- Индексы начала и конца выбранной строки таблицы СИФ-преобразований
k11 = 7 * (j2 - 1) + 1
k22 = k11 + 5
)
-- Находит границы изображения фрактала и устанавливает видовой порт в этих границах
-- Далее эти границы используются для масштабирования изображения
-- и пересчета координат его текущей точки
fn fConv nPAll = (
local k1, k2
xA = yA = -1e3
xI = yI = 1e3
sPoint()
for k = 1 to nPAll do (
findK12 &k1 &k2
col = for m = k1 to k2 collect ifs[m]
affine col &xP &yP
xA = amax #(xP, xA); yA = amax #(yP, yA)
xI = amin #(xP, xI); yI = amin #(yP, yI)
)
viewport.ZoomToBounds false [xI, 0, yI] [xA, 0, yA]
)
-- Формирует фрактальное изображение из nPAll точек
fn showFrctB = (
-- Массив четырех СИФ-преоразований, задающих фрактальную решетку
-- Отражает таблицу СИФ-преоразований
ifs = #(0.3, -0.3, 0.3, 0.3, 1, 1, 0.25,
0.3, -0.3, 0.3, 0.3, 1, -1, 0.25,
0.3, -0.3, 0.3, 0.3, -1, 1, 0.25,
0.3, -0.3, 0.3, 0.3, -1, -1, 0.25)
ifsCnt = ifs.Count
-- nPAll - число точек в изображении фрактала
nPAll = 10000
xP = yP = 1.0
fConv nPAll
bSz = 200
-- Создаем растровый образ размера 200 * 200 пикселей
btmp = bitmap bSz bSz color:white
-- Коэффициенты для пересчета координат точки изображения
-- Изображение вписывается в заданный растровый образ
c = 0.8
cx = c * bSz / (xA - xI)
cy = c * bSz / (yA - yI)
d = 0.5 * (1.0 - c) * bSz
clr = color 0 0 255
k1 = k2 = 0
-- Получаем nPAll точек изображения
-- и фиксируем их в виде синих пикселей растрового образа btmp
-- Начало координат растрового образа в его левом верхнем углу
for k = 1 to nPAll do (
-- Выбираем СИФ-преобразование
findK12 &k1 &k2
col = for m = k1 to k2 collect ifs[m]
-- Находим координаты очередной точки изображения
affine col &xP &yP
xb = d + cx * (xP - xI)
yb = bSz - (d + cy * (yP - yI))
setPixels btmp [xb, yb] #(clr)
)
-- Показываем результат (см. рис. 1)
display btmp
)
showFrctB()
Запуск программы выполняется в 3ds Max в следующем порядке:
Для получения иного изображения достаточно определить массив ifs другими подходящими данными. Эти данные можно взять из кода, приведенного в нижерасположенном разделе "Коллекция Particle Flow-фракталов". Так, если массив ifs определить данными 8-го рисунка
ifs = #(0.824074, 0.281482, -0.212346, 0.864198, -1.882290, -0.110607, 0.787473,
0.088272, 0.520988, -0.463889, -0.377778, 0.785360, 8.095795, 0.212527)
то программа создаст растровый образ фрактального дракона (рис. 2).
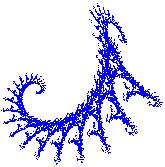
Рис. 2. После замены массива ifs
При формировании СИФ-фрактала из частиц Particle Flow возникают дополнительные возможности по управлению изображением, обусловленные имеющимися в Particle Flow ресурсами.
Ниже следует код, генерирующий СИФ-решетку из крестообразных частиц (рис. 3).

Рис. 3. Фрактальная решетка (построена из частиц)
В отличие от предыдущего варианта вывод, выполняемый в proceed-обработчике оператора script_Operator системы частиц Particle Flow, направляется в видовое окно. При этом определяется позиция только что рожденных частиц. Позиция старых частиц остается неизменной.
Код, как и в случае растрового образа, основан на вышеприведенных алгоритмах построения СИФ-изображения.
global ifs, nPPrev, xP, yP, ifsCnt
-- Подготовка сцены
function tSttngs = (
delete $*
viewport.SetLayout #layout_4
viewport.ActiveViewport = 2
viewport.SetType #view_front
viewport.SetGridVisibility 2 false
sliderTime = 0f
animationRange = interval 0f 50f
timeConfiguration.RealTimePlayback = false
timeConfiguration.PlaybackLoop = false
)
global ifs, xP, yP, ifsCnt
global xI, yI, xA, yA
-- Вычисляет координаты очередной точки изображения фрактала
-- Параметры x и y передаются по ссылке
fn affine col &x &y = (
t = x * col[1] + y * col[2] + col[5]
y = x * col[3] + y * col[4] + col[6]
x = t
)
-- Находит начальную точку изображения
fn sPoint = (
-- Берем первое СИФ-преобразование
col = for k = 1 to 6 collect ifs[k]
-- После 100 итераций xP и yP – это координаты начальной точки
for k = 1 to 100 do affine col &xP &yP
)
-- Выбирает, используя датчик случайных чисел и вероятности выбора,
-- СИФ-преобразование для вычисления координат очередной точки изображения
fn findK12 &k11 &k22 = (
-- Получаем случайное число из диапазона 0.0 – 1.0
r = random 0.0 1.0
p = 0.0
-- j2 – число строк в таблице СИФ-преобразований
j2 = ifsCnt / 7
j3 = j2 - 1
for j = 1 to j3 do (
p += ifs[7 * j]
if r <= p then (j2 = j; exit)
)
-- Индексы начала и конца выбранной строки таблицы СИФ-преобразований
k11 = 7 * (j2 - 1) + 1
k22 = k11 + 5
)
-- Находит границы изображения фрактала и устанавливает видовой порт в этих границах
-- Далее эти границы используются для масштабирования изображения
-- и пересчета координат его текущей точки
fn fConv nPAll = (
local k1, k2
xA = yA = -1e3
xI = yI = 1e3
sPoint()
for k = 1 to nPAll do (
findK12 &k1 &k2
col = for m = k1 to k2 collect ifs[m]
affine col &xP &yP
xA = amax #(xP, xA); yA = amax #(yP, yA)
xI = amin #(xP, xI); yI = amin #(yP, yI)
)
viewport.ZoomToBounds false [xI, 0, yI] [xA, 0, yA]
)
fn showFrct = (
-- Массив четырех СИФ-преоразований, задающий фрактальную решетку
-- Отражает таблицу СИФ-преоразований
ifs = #(0.3, -0.3, 0.3, 0.3, 1, 1, 0.25,
0.3, -0.3, 0.3, 0.3, 1, -1, 0.25,
0.3, -0.3, 0.3, 0.3, -1, 1, 0.25,
0.3, -0.3, 0.3, 0.3, -1, -1, 0.25)
ifsCnt = ifs.Count
-- nPAll - число точек в изображении фрактала
local nPAll = 10000, emS = 0.8 * 160 * 50
xP = yP = 1.0
fConv nPAll
nPPrev = 1
-- Создаем источник частиц с операторами рождения (Birth)
-- и отображения (DisplayParticles) частиц
-- Также источник частиц имеет оператор script_Operator,
-- обеспечивающий нахождение координат только что родившихся частиц
pF = PF_Source enable_Particles:true emitter_Type:0 \
quantity_Viewport:100 show_Logo:off show_Emitter:off
particleFlow.BeginEdit()
opBth = birth emit_Start:0 emit_Stop:emS amount:nPAll
-- Отображаем в видовом порте крестообразную частицу (type = 2)
opDP = displayParticles color:blue type:2
opSO = script_Operator proceed_Script:"
-- Каналы передачи данных
on channelsUsed pCont do (
pCont.UseTime = true
pCont.UsePosition = true
)
on proceed pCont do (
k1 = k2 = 0
nP = pCont.NumParticles()
-- Параметр nPPrev введен для сокращения перебора
for k = nPPrev to nP do (
pCont.ParticleIndex = k
-- Берем только новые частицы
if pCont.ParticleNew do (
-- Выбираем СИФ-преобразование
findK12 &k1 &k2
col = for m = k1 to k2 collect ifs[m]
-- Находим координаты частицы (очередной точки изображения)
affine col &xP &yP
pCont.ParticlePosition = [xP, 0, yP]
)
)
nPPrev = nP
)"
evn = event()
particleFlow.EndEdit()
evn.AppendAction opBth
evn.AppendAction opDP
evn.AppendAction opSO
pF.AppendInitialActionList evn
playAnimation()
)
-- Готовим сцену
tSttngs()
-- Строим изображение
showFrct()
Добавим теперь в сцену бомбу, которая взрывается на 10-м кадре, и взрыв длится 25 кадров:
pb = PBomb symmetry:0 chaos:10 start_Time:10f lasts_For:25f strength:0.1
Для ее учета добавим в источник частиц следующий оператор Force:
opFrc = force force_Space_Warps:#(pb) influence:25
Следующую строку кода поместим перед методом AppendInitialActionList:
evn.AppendAction opFrc
Наблюдаемый результат приведем на рис. 4.

Рис. 4. Решетка с бомбой (40-й кадр анимации)
Приводимый ниже код строит фрактальные объекты на основе системы итерируемых функций (СИФ), а также фрактальные множества Мандельброта и Жюлиа (рис. 5 и 6).

Рис. 5. Множество Мандельброта
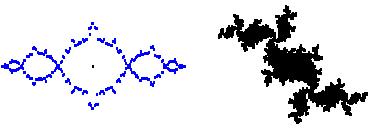
Рис. 6. Множества Жюлиа
Кроме того, демонстрируется морфинг двух СИФ.
Фрактальные объекты и программы их воспроизведения широко представлены в Сети (см., например, статью "Фрактал в Большой Советской Энциклопедии"). Особенности этой программы в том, что, во-первых, в ней собраны СИФ генерации более 80 объектов. Во-вторых, фракталы создаются, как системы частиц, что позволяет манипулировать ими, применяя подходящие 3ds Max-средства управления частицами.
Для запуска исходный ms-код отрывается в редакторе MAXSript, окно с кодом активизируется и затем нажимается Ctrl+E. Появляющийся управляющий диалог приведен на рис. 7.
Рис. 7. Управляющий диалог
global ifs, nPPrev, xP, zP, ifsCnt
global usbNm = "E:\\"
global frmCnt
function apActFn pF arrOps hasRP = (
local evn
evn = event()
arrCnt = if hasRP then arrOps.Count - 1 else arrOps.Count
for k = 1 to arrCnt do evn.AppendAction arrOps[k]
if hasRP do pF.AppendAction arrOps[arrCnt + 1]
particleFlow.EndEdit()
pF.AppendInitialActionList evn
return evn
)
function tSttngs vPn frmCnt rtp gVsb dspBkg sef = (
delete $*
viewport.SetLayout #layout_4
viewport.ActiveViewport = vPn
if vPn == 2 then
viewport.SetType #view_front
else
viewport.SetType #view_persp_user -- Or: max vpt persp user
viewport.SetGridVisibility vPn gVsb
viewport.SetRenderLevel #smoothhighlights
viewport.SetShowEdgeFaces sef
sliderTime = 0f
animationRange = interval 0f frmCnt
timeConfiguration.RealTimePlayback = rtp
timeConfiguration.PlaybackLoop = false
timeConfiguration.PlaybackSpeed = 3 -- 1x
max tool zoomExtents
clearListener()
gc()
return frmCnt
)
fn julia cP showBrd = (
delete $*
sliderTime = 0f
aRng = 100
animationRange = interval 0f aRng
global nChk = 500, k2 = 2.0, c = #(0, 0), emSF = 0.5 * aRng, addF = 5
global notTstd = true, notDltd = true, arrPSt = "Arry arrP is created"
local nPAll = 20000, dpTp = 1, emS = emSF * 160
c = #(cP[1], cP[2])
global xL, xR, yL, yU, dx, dy
xL = yL = k2; xR = yU = -k2
for k = 1 to nPAll do (
x = random -k2 k2
y = random -k2 k2
z = #(x, y)
flg = true
for j = 1 to nChk do (
z = #(z[1] * z[1] - z[2] * z[2] + c[1], 2 * z[1] * z[2] + c[2])
z2 = z[1] * z[1] + z[2] * z[2]
if z2 > 4.0 do (flg = false; exit)
)
if flg do (
xL = amin #(x, xL); yL = amin #(y, yL)
xR = amax #(x, xR); yU = amax #(y, yU)
)
)
nX = 150; nY = 100
dx = (xR - xL) / nX
dy = (yU - yL) / nY
nPAll2 = 1.5 * nX * nY
xR += 5 * dx
global xC = xL - dx, yC = yL - dy
nPPrev = 1
pF = PF_Source enable_Particles:true emitter_Type:0 \
quantity_Viewport:100 show_Logo:off show_Emitter:off
particleFlow.BeginEdit()
opBth = birth emit_Start:0 emit_Stop:emS amount:nPAll2
opDP = displayParticles color:black type:dpTp -- 1 - Dots; 2 - Ticks; 3 - Circles; 9 - Asterisks (6 - Geometry)
opSO = script_Operator proceed_Script:"
on channelsUsed pCont do (
pCont.UseTime = true
pCont.UsePosition = true
)
on proceed pCont do (
nP = pCont.NumParticles()
for k = nPPrev to nP do (
pCont.ParticleIndex = k
if pCont.ParticleNew do (
yC += dy
if yC > yU do (yC = yL; xC += dx)
if xC > xR then exit
z = #(xC, yC)
flg = true
for j = 1 to nChk do (
z = #(z[1] * z[1] - z[2] * z[2] + c[1], 2 * z[1] * z[2] + c[2])
z2 = z[1] * z[1] + z[2] * z[2]
if z2 > 4.0 do (flg = false; exit)
)
if flg do pCont.ParticlePosition = [xC, 0, yC]
)
)
nPPrev = nP
)"
if showBrd then (
tstST = script_Test proceed_Script:"
on channelsUsed pCont do (
pCont.UseTime = true
pCont.UsePosition = true
)
on proceed pCont do (
if sliderTime > emSF + addF and notTstd do (
notTstd = false
nP = pCont.NumParticles()
for k = 1 to nP do (
pCont.ParticleIndex = k
pPs = pCont.ParticlePosition
if pPs[1] != 0 and pPs[3] != 0 then (
pCont.ParticleTestStatus = true
pCont.ParticleTestTime = pCont.ParticleTime
)
)
)
)"
apActFn pF #(opBth, opDP, opSO, tstST) false
--
-- Event 2
particleFlow.BeginEdit()
opDP2 = displayParticles type:dpTp color:red
tstST2 = script_Test proceed_Script:"
on channelsUsed pCont do (
pCont.UseTime = true
pCont.UsePosition = true
)
on proceed pCont do (
if sliderTime > emSF + 3 * addF and notDltd do (
notDltd = false
nP = pCont.NumParticles()
arrP = #()
x = xL - dx
while x < xR do (
x += dx
arrAdd = #()
for k = 1 to nP do (
pCont.ParticleIndex = k
pPs = pCont.ParticlePosition
xP = pPs[1]
if xP == x do append arrAdd k
)
append arrP arrAdd
)
print arrPSt
x = xL - dx
n = 0
while x < xR do (
x += dx
n += 1
arrCr = arrP[n]
cnt = arrCr.Count
if cnt > 0 do (
pCont.ParticleIndex = arrCr[1]
pCont.ParticleTestStatus = true
pCont.ParticleTestTime = pCont.ParticleTime
pCont.ParticleIndex = arrCr[cnt]
pCont.ParticleTestStatus = true
pCont.ParticleTestTime = pCont.ParticleTime
cnt1 = cnt - 1
for j = 2 to cnt1 do (
pCont.ParticleIndex = arrCr[j - 1]
pPs0 = pCont.ParticlePosition
pCont.ParticleIndex = arrCr[j + 1]
pPs2 = pCont.ParticlePosition
pCont.ParticleIndex = arrCr[j]
pPs = pCont.ParticlePosition
zP = pPs[3]
if zP > pPs0[3] + dY and zP < pPs2[3] - dY then(
pCont.ParticleTestStatus = true
pCont.ParticleTestTime = pCont.ParticleTime
)
)
)
)
)
)"
tstAg2 = age_Test test_Type:2 test_Value:(160 * 4 * addF) variation:0
evn2 = apActFn pF #(opDP2, tstST2, tstAg2) false
tstST.SetNextActionList evn2 tstST
--
-- Event 3
particleFlow.BeginEdit()
opDP3 = displayParticles type:dpTp color:blue
evn3 = apActFn pF #(opDP3) false
tstST2.SetNextActionList evn3 tstST2
--
-- Event 4
particleFlow.BeginEdit()
opDlt4 = deleteParticles type:0
evn4 = apActFn pF #(opDlt4) false
tstAg2.SetNextActionList evn4 tstAg2
)
else
apActFn pF #(opBth, opDP, opSO) false
--
xz = 2.0
viewport.ZoomToBounds false [-xz, 0, -xz] [xz, 0, xz]
timeConfiguration.RealTimePlayback = false
playAnimation()
)
fn mndlbrt h = (
delete $*
sliderTime = 0f
aRng = 100
animationRange = interval 0f aRng
local nPAll = 10000, emS = 0.8 * 160 * aRng, dpTp = 9
global nChk = 300, k2 = sqrt 2.0
nPPrev = 1
pF = PF_Source enable_Particles:true emitter_Type:0 \
quantity_Viewport:100 show_Logo:off show_Emitter:off
particleFlow.BeginEdit()
opBth = birth emit_Start:0 emit_Stop:emS amount:nPAll
-- 1 - Dots; 2 - Ticks; 3 - Circles; 9 - Asterisks (6 - Geometry)
opDP = displayParticles color:black type:dpTp
opSO = script_Operator proceed_Script:"
on channelsUsed pCont do (
pCont.UseTime = true
pCont.UsePosition = true
)
on proceed pCont do (
nP = pCont.NumParticles()
for k = nPPrev to nP do (
pCont.ParticleIndex = k
if pCont.ParticleNew do (
r1 = pCont.Rand11()
r2 = pCont.Rand11()
c = #(k2 * r1, k2 * r2)
z = #(0.0, 0.0)
flg = true
for j = 1 to nChk do (
z = #(z[1] * z[1] - z[2] * z[2] + c[1], 2 * z[1] * z[2] + c[2])
z2 = z[1] * z[1] + z[2] * z[2]
if z2 > 4.0 do (flg = false; exit)
)
if flg do pCont.ParticlePosition = [c[1], 0, c[2] + 0.2]
)
)
nPPrev = nP
)"
apActFn pF #(opBth, opDP, opSO) false
xz = 1.0
viewport.ZoomToBounds false [-xz, 0, -xz] [xz, 0, xz]
timeConfiguration.RealTimePlayback = false
playAnimation()
)
fn affine col &x &y = (
t = x * col[1] + y * col[2] + col[5]
y = x * col[3] + y * col[4] + col[6]
x = t
)
fn sPoint = (
col = for k = 1 to 6 collect ifs[k]
for k = 1 to 100 do affine col &xP &zP
)
fn findK12 &k11 &k22 = (
r = random 0.0 1.0
p = 0.0
j2 = ifsCnt / 7
j3 = j2 - 1
for j = 1 to j3 do (
p += ifs[7 * j]
if r <= p then (j2 = j; exit)
)
k11 = 7 * (j2 - 1) + 1
k22 = k11 + 5
)
fn fConv nPAll = (
local k1, k2
xA = zA = -1e3
xI = zI = 1e3
sPoint()
for k = 1 to nPAll do (
findK12 &k1 &k2
col = for m = k1 to k2 collect ifs[m]
affine col &xP &zP
xA = amax #(xP, xA); zA = amax #(zP, zA)
xI = amin #(xP, xI); zI = amin #(zP, zI)
)
viewport.ZoomToBounds false [xI, 0, zI] [xA, 0, zA]
)
fn showFrct h = (
ifs = case h of (
1 : #(0.04, 0.22, 0.31, -0.03, 0.63, -1.74, 0.13,
-0.02, 0.0, -0.32, 0.26, -0.17, -1.35, 0.01,
0.79, 0.06, -0.03, 0.73, -0.02, 1.03, 0.74,
-0.03, -0.3, 0.35, -0.04, -0.68, -0.94, 0.12)
2 : #(0.00, 0.00, 0.00, -0.50, 0.00, 0.00, 0.05,
0.42, -0.42, 0.42, 0.42, 0.00, 0.20, 0.40,
0.42, 0.42, -0.42, 0.42, 0.00, 0.20, 0.40,
0.10, 0.00, 0.00, 0.10, 0.00, 0.20, 0.15)
3 : #(-0.50, -0.30, 0.30, -0.50, -6.07, -3.58, 0.33,
-0.50, -0.29, 0.29, -0.50, 5.92, 3.50, 0.33,
0.00, -0.59, 0.59, 0.00, -0.09, -0.04, 0.34,
0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00)
4 : #(0.14, 0.01, 0.00, 0.51, -0.08, -1.31, -0.06,
0.43, 0.52, -0.45, 0.50, 1.49, -0.75, 0.37,
0.45, -0.49, 0.47, 0.47, -1.62, -0.74, 0.36,
0.49, 0.00, 0.00, 0.51, 0.02, 1.62, 0.21)
5 : #(0.50, 0.00, 0.00, 0.50, 0.00, 0.00, 0.333333,
0.50, 0.00, 0.00, 0.50, 0.5, 0.00, 0.333333,
0.00, -0.50, 0.50, 0.00, 1.00, 0.50, 0.333333)
6 : #(0.307692, -0.531469, -0.461538, -0.293706, 5.401953, 8.655175, 0.4,
0.307692, -0.076923, 0.153846, -0.447552, -1.295248, 4.152990, 0.15,
0.00, 0.545455, 0.692308, -0.195804, -4.893637, 7.269794, 0.45)
7 : #(0.696970, -0.481061, -0.393939, -0.662879, 2.147003, 10.310288, 0.747826,
0.090909, -0.443182, 0.515552, -0.094697, 4.286558, 2.925762, 0.252174)
8 : #(0.824074, 0.281482, -0.212346, 0.864198, -1.882290, -0.110607, 0.787473,
0.088272, 0.520988, -0.463889, -0.377778, 0.785360, 8.095795, 0.212527)
9 : #(0.00, 0.00, 0.00, 0.16, 0.00, 0.00, 0.001,
0.85, 0.04, -0.04, 0.85, 0.00, 1.6, 0.85,
0.20, -0.26, 0.23, 0.22, 0.00, 1.60, 0.07,
-0.15, 0.28, 0.26, 0.24, 0.00, 0.44, 0.07)
10 : #(0.00, -0.50, 0.50, 0.00, -0.25, 0.00, 0.333333,
0.50, 0.00, 0.00, 0.50, 0.00, 0.25, 0.333333,
0.00, 0.50, -0.50, 0.00, 0.25, 0.00, 0.333333)
11 : #(0.3333, 0.00, 0.00, 0.3333, 0.00, 0.00, 0.25,
0.1677, -0.2887, 0.2887, 0.1677, 0.3333, 0.00, 0.25,
-0.1677, 0.2887, 0.2887, 0.1677, 0.6666, 0.00, 0.25,
0.3333, 0.00, 0.00, 0.3333, 0.6666, 0.00, 0.25)
12 : #(0.787879, -0.424242, 0.242424, 0.859848, 1.758647, 1.408065, 0.895652,
-0.121212, 0.257576, 0.151515, 0.053030, -6.721654, 1.377326, 0.052174,
0.181818, -0.136364, 0.090909, 0.181818, 6.086107, 1.568035, 0.052174)
13 : #(0.745455, -0.459091, 0.406061, 0.887121, 1.460279, 0.691072, 0.912675,
-0.424242, -0.065152, -0.175758, -0.218182, 3.809567, 6.741476, 0.087325)
14 : #(0.50, 0.00, 0.00, 0.50, 0.00, 0.50, 0.33333,
0.50, 0.00, 0.00, 0.50, -0.25, 0.00, 0.33333,
0.50, 0.00, 0.00, 0.50, 0.25, 0.00, 0.33333)
15 : #(-0.40, 0.00, 0.00, -0.40, 0.24, 0.37, 0.23,
0.50, 0.00, 0.00, 0.50, -1.37, 0.25, 0.36,
0.21, 0.00, 0.00, 0.21, 1.00, 1.47, 0.06,
0.50, 0.00, 0.00, 0.50, 0.76, -1.16, 0.36)
16 : #(-0.632407, -0.614815, -0.545370, 0.659259, 3.840822, 1.282321, 0.888128,
-0.036111, 0.444444, 0.210185, 0.037037, 2.071081, 8.330552, 0.111872)
17 : #(0.307692, 0.00, 0.00, 0.294118, 4.136530, 1.604278, 0.20,
0.192308, -0.205882, 0.653846, 0.0882235, -0.688840, 5.978916, 0.30,
-0.192308, 0.205882, 0.653846, 0.0882235, 0.688840, 5.978916, 0.30,
0.307692, 0.00, 0.00, 0.294118, -4.136530, 1.604278, 0.20)
18 : #(0.00, 0.00, 0.00, -0.50, 0.00, 0.00, 0.05,
0.42, -0.42, 0.42, 0.42, 0.00, 0.20, 0.40,
0.42, 0.42, -0.42, 0.42, 0.00, 0.20, 0.40,
0.10, 0.00, 0.00, 0.10, 0.00, 0.20, 0.15)
19 : #(0.50, -0.50, 0.50, 0.50, 0.00, 0.00, 0.5,
-0.50, 0.5, -0.50, -0.50, 1.5, 0.5, 0.5,
0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00,
0.00, 0.00, 0.00, 0.00, 0.00, 0.00, 0.00)
20 : #(0.5, 0, 0, 0.3, 0, 0, 0.246154,
0.5, 0, 0, 0.3, 0.5, 0, 0.246154,
0.5, 0, 0, 0.7, 0.25, 0.3, 0.507692)
21 : #(0.3, -0.3, 0.3, 0.3, 1, 1, 0.25,
0.3, -0.3, 0.3, 0.3, 1, -1, 0.25,
0.3, -0.3, 0.3, 0.3, -1, 1, 0.25,
0.3, -0.3, 0.3, 0.3, -1, -1, 0.25)
22 : #(0.47, 0.17, -0.17, 0.47, 0.00, 0.00, 0.45,
-0.11, 0.77, -0.77, -0.11, 1.11, 0.77, 0.55)
23 : #(-0.81, -0.38, 0.38, -0.81, 0.0, 0.00, 0.83,
-0.30, 0.25, -0.25, -0.30, 1.3, 0.25, 0.17)
24 : #(0.5, 0, 0, -0.5, 0.00, 0.000000, 0.3333,
0.5, 0, 0, -0.5, 0.50, 0.000000, 0.3333,
0.5, 0, 0, -0.5, 0.25, 0.433013, 0.3333)
25 : #(0.358591, 0.329160, -0.334007, 0.580720, -5.889050, 1.924278, 0.361396,
0.796218, 0.136942, 0.075187, 0.719074, 1.086998, 0.408452, 0.638604)
26 : #(0.833333, 0.333333, -0.446667, 0.253333, -0.729257, 3.228710, 0.480522,
0.447556, 0.134222, -0.413778, 0.326222, 1.905433, 5.822160, 0.269013,
-0.286667, -0.186667, 0.531556, -0.308444, -2.854176, 4.504472, 0.250465)
27 : #(0.424242, -0.651515, -0.484848, -0.344697, 3.442830, 2.889184, 0.622449,
0.030303, -0.439394, -0.636364, -0.022727, -1.425239, 6.437284, 0.377551)
28 : #(0.636364, -0.727273, -0.515152, -0.405303, 3.395211, 5.032732, 0.826733,
0.151515, -0.321970, 0.484848, -0.155303, -3.669363, 5.726923, 0.173267)
29 : #(0.788060, -0.552239, -0.391045, -0.835821, 2.852489, 7.293853, 0.912773,
-0.134328, -0.462687, -0.137313, 0.149254, -4.167883, 5.968212, 0.087227)
30 : #(-0.548060, -0.181095, 0.257313, -1.015920, -1.126466, 10.341689, 0.760052,
-0.049353, -0.415920, 0.440398, -0.148259, 3.405604, 3.257883, 0.239948)
31 : #(0.50, 0, 0, 0.3, 0.0, 0.4, 0.25,
0.3, 0, 0, 0.50, -0.4, 0.0, 0.25,
0.3, 0, 0, 0.50, 0.4, 0.0, 0.25,
0.50, 0, 0, 0.3, 0.0, -0.4, 0.25)
32 : #(0.860671, 0.401487, -0.402177, 0.860992, 0.108537, 0.075138, 0.956972,
0.094957, -0.000995, 0.237023, 0.002036, -0.746911, 0.047343, 0.009813,
0.150288, 0.000000, 0.000000, 0.146854, -0.563199, 0.032007, 0.023402,
0.324279, -0.002163, 0.005846, 0.001348, -0.557936, -0.139735, 0.009813)
33 : #(0.5, 0.5, 0.5, -0.5, 0.0, 0.0, 0.5,
0.6, -0.2, -0.2, -0.6, 0.4, 0.2, 0.5)
34 : #(0.0, -0.7, 0.7, 0.0, 0.0, 0.0, 0.5,
0.7, 0.0, 0.0, 0.7, 0.3, 0.0, 0.5)
35 : #(0.5, 0.288675, 0.288675, -0.5, 0.0, 0.000000, 0.5,
0.5, -0.288675, -0.288675, -0.5, 0.5, 0.288675, 0.5)
36 : #(0.60, -0.6, 0.6, 0.60, 0.00, 0.0, 0.5,
0.53, 0.0, 0.0, 0.53, 0.47, 0.0, 0.5)
37 : #(0.5, 0.5, -0.5, 0.5, -1.0, 0.0, 0.5,
0.5, 0.5, 0.5, -0.5, 0.0, 1.0, 0.5)
38 : #(0.1000, 0.00, 0.00, 0.16, 0.0, 0.0, 0.01,
0.8500, 0.00, 0.00, 0.85, 0.0, 1.6, 0.85,
-0.1667, -0.2887, 0.2887, -0.1667, 0.0, 1.6, 0.07,
-0.1667, 0.2887, -0.2887, -0.1667, 0.0, 1.6, 0.07)
39 : #(-0.61, 0.7, -0.7, -0.61, 0.0, 0.0, 0.9,
0.21, 0.0, 0.0, 0.21, 0.79, 0.0, 0.1)
40 : #(0.7, 0.2, -0.2, 0.7, 0.0, 0.0, 0.5,
0.0, -0.6, 0.6, 0.0, 1.0, -0.6, 0.5)
41 : #(0.2, -0.3, 0.3, 0.2, 0.0, 0.0, 0.3,
0.5, 0.7, -0.7, 0.5, 0.5, 0.7, 0.7)
42 : #(-0.75, -0.30, 0.30, -0.75, 0.0, 0.00, 0.7,
0.30, -0.35, 0.35, 0.30, 0.7, -0.35, 0.3)
43 : #(0.46, 0, 0, 0.46, 0.54, 0, 0.25,
0.46, 0, 0, 0.46, -0.54, 0, 0.25,
0.46, 0, 0, 0.46, 0, 0.54, 0.25,
0.46, 0, 0, 0.46, 0, -0.54, 0.25)
44 : #(-0.92, -0.09, 0.09, -0.92, 0.00, 0.00, 0.1,
0.79, 0.26, -0.26, 0.79, 0.21, 0.26, 0.9)
45 : #(-0.81, -0.26, 0.26, -0.81, 0.00, 0.00, 0.65,
-0.38, 0.23, -0.23, -0.38, 1.38, 0.23, 0.35)
46 : #(-0.4, 0.51, -0.51, -0.4, 0.0, 0.00, 0.5,
-0.4, -0.51, 0.51, -0.4, 1.4, -0.51, 0.5)
47 : #(-0.5, -0.43, 0.43, -0.5, 0.0, 0.00, 0.55,
-0.5, 0.43, -0.43, -0.5, 1.5, 0.43, 0.45)
48 : #(0.5, 0.66, -0.66, 0.5, 0.0, 0.0, 0.77,
0.0, 0.50, -0.50, 0.0, 1.0, 0.5, 0.23)
49 : #(0.0, 0.77, -0.77, 0.0, 0.0, 0.0, 0.65,
0.0, -0.50, 0.50, 0.0, 1.0, -0.5, 0.35)
50 : #(-0.75, -0.4, 0.4, -0.75, 0.00, 0.0, 0.79,
0.09, -0.4, 0.4, 0.09, 0.91, -0.4, 0.21)
51 : #(0.38, 0.21, -0.21, 0.38, 1, 1, 0.25,
0.38, 0.21, -0.21, 0.38, -1, 1, 0.25,
0.38, 0.21, -0.21, 0.38, 1, -1, 0.25,
0.38, 0.21, -0.21, 0.38, -1, -1, 0.25)
52 : #(-0.87, 0.23, -0.23, -0.87, 0.0, 0.00, 0.8,
0.30, 0.21, -0.21, 0.30, 0.7, 0.21, 0.2)
53 : #(-0.87, 0.23, -0.23, -0.87, 0.00, 0.00, 0.8,
-0.34, 0.21, -0.21, -0.34, 1.34, 0.21, 0.2)
54 : #(0.83, -0.43, 0.43, 0.83, 0.00, 0.00, 0.89,
0.21, 0.21, -0.21, 0.21, 0.79, 0.21, 0.11)
55 : #(0.255, 0.000, 0.000, 0.255, 0.1146, 0.2232, 0.15,
0.255, 0.000, 0.000, 0.255, 0.3726, 0.6714, 0.15,
0.255, 0.000, 0.000, 0.255, 0.6306, 0.2232, 0.15,
0.370, -0.642, 0.642, 0.370, 0.6356, -0.0061, 0.55)
56 : #(0.307692, 0.000000, 0.000000, 0.294118, 4.119164, 1.604278, 0.151515,
0.192308, -0.205882, 0.653846, 0.088235, -0.688840, 5.978916, 0.253788,
0.192308, 0.205882, -0.653846, 0.088235, 0.668580, 5.962514, 0.253788,
0.307692, 0.000000, 0.000000, 0.294118, -4.136530, 1.604278, 0.151515,
0.384615, 0.000000, 0.000000, -0.294118, -0.007718, 2.941176, 0.189394)
57 : #(0.195, -0.488, 0.344, 0.443, 0.4431, 0.2452, 0.25,
0.462, 0.414, -0.252, 0.361, 0.2511, 0.5692, 0.25,
-0.058, -0.070, 0.423, -0.111, 0.5976, 0.0969, 0.15,
-0.035, 0.070, -0.469, 0.022, 0.4884, 0.5069, 0.15,
-0.637, 0.000, 0.000, 0.501, 0.8562, 0.2513, 0.20)
58 : #(0.5, 0, 0.4, 0.1, 1.0, 1.2, 0.2,
0.5, 0, 0.0, 0.1, 0.0, 2.0, 0.2,
0.5, 0, 0.0, 0.1, 1.0, 2.0, 0.2,
0.5, 0, -0.4, 0.1, 1.0, 2.8, 0.2,
0.5, 0, 0.0, 0.1, -1.0, 2.0, 0.2)
59 : #(0.5, 0.0, 0.4, 0.1, 1.00, 1.20, 0.14,
0.5, 0.0, 0.0, 0.1, 1.00, 2.00, 0.14,
0.5, 0.0, -0.4, 0.1, 1.00, 2.80, 0.14,
0.5, 0.0, 0.0, 0.1, -1.00, 2.00, 0.14,
0.5, 0.0, 0.4, 0.1, -1.00, 2.80, 0.14,
0.5, 0.0, -0.4, 0.1, -1.00, 1.20, 0.14,
0.0, 0.1, 0.8, 0.0, -0.22, 2.22, 0.14)
60 : #(0.5, 0, 0.4, 0.1, 1.0, 1.0, 0.19,
1.2, 0, 0.0, 0.1, -0.4, 2.0, 0.24,
0.5, 0, -0.4, 0.1, 1.0, 3.0, 0.19,
0.5, 0, 0.4, 0.1, -1.0, 3.0, 0.19,
0.5, 0, -0.4, 0.1, -1.0, 1.0, 0.19)
61 : #(0.333333, 0.000000, 0.000000, -0.333333, 0.000000, 0.000000, 0.166666,
0.333333, 0.000000, 0.000000, 0.333333, 0.333333, 0.000000, 0.166666,
0.333333, 0.000000, 0.000000, -0.333333, 0.666666, 0.000000, 0.166666,
0.333333, 0.000000, 0.000000, -0.333333, 0.333333, 0.333333, 0.166666,
0.000000, -0.333333, 0.333333, 0.000000, 0.333333, 0.000000, 0.166666,
0.000000, 0.333333, -0.333333, 0.000000, 0.666666, 0.333333, 0.166666)
62 : #(0.284211, -0.356436, 0.326316, 0.445545, 0.006246, 0.562745, 0.166,
0.378947, 0.386139, -0.273684, 0.346535, -0.081705, 0.540626, 0.166,
0.410526, 0.000000, 0.000000, 0.554455, -0.028316, 0.533465, 0.166,
-0.621053, 0.000000, 0.000000, 0.435644, -0.095368, 0.357723, 0.166,
-0.031579, -0.079208, 0.557895, -0.089109, -0.007548, 0.511956, 0.166,
-0.084211, 0.089109, -0.557895, -0.059406, -0.176167, 0.405866, 0.166)
63 : #(0.336735, 0.000000, 0.000000, 0.330097, -0.161633, 0.610194, 0.143,
0.326531, 0.000000, 0.000000, 0.330097, 0.143265, 0.610194, 0.143,
0.091837, -0.281553, 0.336735, 0.106796, -0.247188, 0.551960, 0.143,
0.275510, -0.174757, 0.214286, 0.271845, -0.061759, 0.370832, 0.143,
0.265306, 0.184466, -0.204082, 0.262136, 0.041585, 0.372231, 0.143,
0.102041, 0.300971, -0.336735, 0.097087, 0.222962, 0.545807, 0.143,
0.326531, 0.000000, 0.010204, 0.339806, -0.006735, 0.104714, 0.143)
64 : #(0.333333, 0, 0, 0.333333, -0.333333, 0.733333, 0.125,
0.333333, 0, 0, 0.333333, -0.033333, 0.733333, 0.125,
0.333333, 0, 0, 0.333333, 0.266667, 0.733333, 0.125,
0.333333, 0, 0, 0.333333, -0.333333, 0.433333, 0.125,
0.333333, 0, 0, 0.333333, 0.266667, 0.433333, 0.125,
0.333333, 0, 0, 0.333333, -0.333333, 0.133333, 0.125,
0.333333, 0, 0, 0.333333, -0.033333, 0.133333, 0.125,
0.333333, 0, 0, 0.333333, 0.266667, 0.133333, 0.125)
65 : #(0.406061, -0.712879, -0.769697, -0.389394, 4.317561, 5.632481, 0.762878,
0.090909, -0.443182, 0.515152, -0.094697, -2.580470, 3.755983, 0.237122)
66 : #(0.5, 0.5, 0.0, 0.0, 0.00, 0.00, 0.166,
0.5, 0.5, 0.0, 0.0, 0.00, 1.00, 0.166,
0.0, 0.0, 0.5, 0.5, 0.00, 0.00, 0.166,
0.0, 0.0, 0.5, 0.5, 1.00, 0.00, 0.166,
0.5, 0.0, 0.0, 0.5, 0.25, 0.25, 0.336)
67 : #(-0.322222, -0.007143, 0.040741, -0.240476, 0.164143, 10.217592, 0.053858,
-0.166667, -0.250000, -0.333333, 0.214286, 3.914220, 3.198747, 0.082436,
-0.166667, 0.250000, 0.333333, 0.214286, -3.819525, 3.171691, 0.082436,
0.111111, -0.285714, -0.166667, -0.107143, 4.455358, 8.163677, 0.041218,
0.155556, -0.257143, -0.207407, -0.133333, -1.593255, 8.570432, 0.051293,
-0.222222, 0.000000, 0.000000, 0.428571, 0.049603, -0.129243, 0.065949,
0.944444, -0.007143, -0.007407, 0.952381, 0.038005, 0.363189, 0.622811)
68 : #(0.1665, -0.288386, 0.288386, 0.1665, -1.569386, 2.432818, 0.142857,
0.333, 0, 0, 0.333, -0.006, -0.127, 0.142857,
0.1665, 0.288386, -0.288386, 0.1665, 1.563386, 2.440181, 0.142857,
0.333, 0, 0, 0.333, 3.018, 5.093, 0.142857,
0.333, 0, 0, 0.333, -3.006, 5.057, 0.142857,
0.333, 0, 0, 0.333, -0.006, 6.797, 0.142857,
0.333, 0, 0, 0.333, -0.006, 3.329, 0.142857)
69 : #(0.382, 0, 0, 0.382, 3.528, 4.230, 0.2,
0.382, 0, 0, 0.382, -0.024, 6.810, 0.2,
0.382, 0, 0, 0.382, -3.540, 4.230, 0.2,
0.382, 0, 0, 0.382, -2.208, 0.102, 0.2,
0.382, 0, 0, 0.382, 2.196, 0.102, 0.2)
70 : #(0.255, 0, 0, 0.255, 0.006, 7.307, 0.080149,
0.255, 0, 0, 0.255, -3.09, 1.931, 0.080149,
0.255, 0, 0, 0.255, 3.102, 1.931, 0.080149,
0.268485, -0.737658, 0.737658, 0.268485, 3.705256, 3.658438, 0.759552)
71 : #(0.788060, -0.552239, -0.352239, -0.791045, 2.744518, 6.550929, 0.889610,
-0.149254, -0.402985, -0.191045, 0.164179, -4.915581, 5.265871, 0.110390)
72 : #(0.636364, -0.727273, -0.636364, -0.397727, 3.546802, 6.288650, 0.710526,
0.030303, -0.189394, 0.666667, -0.166667, 0.657856, 3.712271, 0.120301,
0.212121, 0.049242, 0.272727, 0.545455, 3.124111, 1.359796, 0.101504,
0.090909, 0.181818, -0.151515, 0.446970, -3.132705, 5.667240, 0.067669)
73 : #(-0.54, -0.58, 0.58, -0.54, 0, 0, 0.61,
-0.41, 0.33, -0.33, -0.41, 1.41, 0.33, 0.39)
74 : #(-0.429709, 0.239060, -0.186789, -0.549960, 3.062810, -0.698988, 0.375,
0.313497, -0.228097, -0.494939, -0.512296, 0.474109, 13.318000, 0.625)
75 : #(-0.62, 0, 0, -0.62, 0, 0, 0.5,
0, -0.6, -0.6, 0, 1, 0.6, 0.5)
76 : #(0.5, 0.5, 0, 0, 0, 0.5, 0.08,
0.5, 0.5, 0, 0, 0, -0.5, 0.08,
0, 0, 0.5, 0.5, 0.5, 0, 0.08,
0, 0, 0.5, 0.5, -0.5, 0, 0.08,
0.85, -0.15, 0.15, 0.85, 0, 0, 0.68)
77 : #(0.62, 0, 0, 0.09, 0, 0, 0.03,
-0.79, 0.55, -0.55, -0.79, 1.79, 0.55, 0.97)
78 : #(0.333333, 0, 0, 0.333333, 0, 0.666667, 0.2,
0.333333, 0, 0, 0.333333, 0.333333, 0.666667, 0.2,
0.333333, 0, 0, 0.333333, 0.666667, 0.666667, 0.2,
0.333333, 0, 0, 0.333333, 0.333333, 0.333333, 0.2,
0.333333, 0, 0, 0.333333, 0.333333, 0, 0.2)
79 : #(0.935567, -0.164966, 0.164966, 0.935567, 0, 0, 0.958,
0.1, 0, 0, 0.1, 0.75, -0.75, 0.011,
0.1, 0, 0, 0.1, -0.75, 0.75, 0.011,
0.1, 0, 0, 0.1, 0.75, 0.75, 0.011,
0.1, 0, 0, 0.1, -0.75, -0.75, 0.009)
80 : #(0.25, 0, 0, 0.25, 1.0, 0, 0.105,
0.125, -0.216506, 0.216506, 0.125, 0.5, 0.866025, 0.105,
-0.125, -0.216506, 0.216506, -0.125, -0.5, 0.866025, 0.105,
-0.25, 0, 0, -0.25, -1.0, 0, 0.105,
-0.125, 0.216506, -0.216506, -0.125, -0.5, -0.866025, 0.105,
0.125, 0.216506, -0.216506, 0.125, 0.5, -0.866025, 0.105,
0.536625, -0.143788, 0.143788, 0.536625, 0, 0, 0.37)
81 : #(0.5, 0, 0.2, 0.4, -0.6, 0, 0.25,
-0.2, 0, 0.2, 0.5, 0.3, 0.8, 0.25,
-0.8, 0, 0, 0.8, 0.1, 0, 0.25,
0.2, 0, 0, 0.6, 0, 0.35, 0.25)
82 : #(0.25, 0, 0, -0.5, 0, 0, 0.25,
0.25, 0, 0, 0.5, 0.25, -0.2, 0.25,
0.25, 0, 0, 0.5, 0.5, 0, 0.25,
0.25, 0, 0, 0.5, 0.75, 0.2, 0.25)
)
if h == 18 then (
ifs1 = #(0.00, 0.00, 0.00, -0.50, 0.00, 0.00, 0.05,
0.42, -0.42, 0.42, 0.42, 0.00, 0.20, 0.40,
0.42, 0.42, -0.42, 0.42, 0.00, 0.20, 0.40,
0.10, 0.00, 0.00, 0.10, 0.00, 0.20, 0.15)
ifs2 = #(0.14, 0.01, 0.00, 0.51, -0.08, -1.31, -0.06,
0.43, 0.52, -0.45, 0.50, 1.49, -0.75, 0.37,
0.45, -0.49, 0.47, 0.47, -1.62, -0.74, 0.36,
0.49, 0.00, 0.00, 0.51, 0.02, 1.62, 0.21)
ifsCnt = ifs1.Count
)
else
ifsCnt = ifs.Count
aRng = 50
animationRange = interval 0f aRng
local nPAll = 4000, emS = 0.8 * 160 * aRng, dpTp = 2
m2 = if h == 18 then 6 else 1
ph = 0.0
for m = 1 to m2 do (
delete $*
sliderTime = 0f
if h == 18 do (
ifs = for i = 1 to ifsCnt collect (1.0 - ph) * ifs1[i] + ph * ifs2[i]
ph += 0.2
)
xP = zP = 1.0
fConv nPAll
nPPrev = 1
pF = PF_Source enable_Particles:true emitter_Type:0 \
quantity_Viewport:100 show_Logo:off show_Emitter:off
particleFlow.BeginEdit()
opBth = birth emit_Start:0 emit_Stop:emS amount:nPAll
-- 1 - Dots; 2 - Ticks; 3 - Circles; 9 - Asterisks (6 - Geometry)
opDP = displayParticles color:green type:dpTp
opSO = script_Operator proceed_Script:"
on channelsUsed pCont do (
pCont.UseTime = true
pCont.UsePosition = true
)
on proceed pCont do (
k1 = k2 = 0
nP = pCont.NumParticles()
for k = nPPrev to nP do (
pCont.ParticleIndex = k
if pCont.ParticleNew do (
findK12 &k1 &k2
col = for m = k1 to k2 collect ifs[m]
affine col &xP &zP
pCont.ParticlePosition = [xP, 0, zP]
)
)
nPPrev = nP
)"
tstAT = age_Test test_Type:1 condition_Type:1 test_Value:(emS / 3) variation:0
apActFn pF #(opBth, opDP, opSO, tstAT) false
-- Event 2
particleFlow.BeginEdit()
opDP2 = displayParticles color:red type:dpTp
tstAT2 = age_Test test_Type:1 condition_Type:1 test_Value:(2 * emS / 3) variation:0
evn2 = apActFn pF #(opDP2, tstAT2) false
tstAT.SetNextActionList evn2 tstAT
-- Event 3
particleFlow.BeginEdit()
opDP3 = displayParticles color:blue type:dpTp
evn3 = apActFn pF #(opDP3) false
tstAT2.SetNextActionList evn3 tstAT2
playAnimation()
)
)
fn fAlPFFr g = (
arrUs = #( 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, \
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, \
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, \
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, \
1, 1, 1, 1, 1, 1, 1, 1)
arrN = #( 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, \
20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, \
36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, \
55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, \
75, 76, 77, 78, 79, 80, 81, 82)
arrNm = #("1 - Curl", "2 - Tree", "3 - Davis", "4 - Leaf", "5 - Binary", \
"6 - Coral", "7 - Crystal", "8 - Dragon", "9 - Fern", \
"10 - Floor", "11 - Koch", "12 - Spiral", "13 - Swirl", "14 - Sierpinski", \
"15 - Triangle", "16 - Zigzag", "17 - Koch2", "18 - Morph", "19 - Dragon_3", \
"20 - Eiffel_Tower", "21 - Lattice", "22 - Goblins", "23 - Web", "24 - Flake", \
"25 - Windy", "26 - Wilting", "27 - Twigs", "28 - Needle", "29 - Scales", \
"30 - Sinewy", "31 - Ball_45", "32 - Nautilus", "33 - Dendrit_1", "34 - Dendrit_2", \
"35 - Koch_curve", "36 - Leaf_3", "37 - Wolfs", "38 - Fir_2", "39 - Spiral_12", \
"40 - Talon", "41 - Spiral_19", "42 - Chain_2", "43 - Square", "44 - Seashell", \
"45 - Branch", "46 - Frog_paws", "47 - Wood", "48 - Spiral_14", "49 - Chess", \
"50 - Chain", "51 - Net", "52 - Spiral_16", "53 - Spiral_17", "54 - Spiral_18", \
"55 - Crystal_2", "56 - Koch_Curve_3", "57 - Tree_2", "58 - Arrow", "59 - Diamond_2", \
"60 - Fish", "61 - Mandelbrot_GC", "62 - Tree_3", "63 - Parachute", "64 - Sierpinsky_3", \
"65 - Jagged", "66 - Boxes", "67 - Shooter", "68 - A_n_flake", "69 - Pentagon_3", \
"70 - First_star", "71 - Zigzag0", "72 - Neuron", "73 - Break_4", "74 - Atilla", \
"75 - Corner_35", "76 - Stairway", "77 - Star_55", "78 - Tee_3x3", "79 - Spiral_54", \
"80 - Snowflake-Dancing", "81 - Mountains2", "82 - Kieswetter")
cnt = pFIFS.Controls.Count
for h = 1 to 82 do
if arrUs[h] == 1 do (
if shMsg do messageBox(arrNm[h])
pFIFS.Controls[cnt].Text = pFIFS.Controls[h].Caption
showFrct h
)
pFIFS.Controls[cnt].Text = ""
if g do (
mndlbrt 1
julia #(-1.0, 0.0) true
julia #(-0.2, 0.75) false
julia #(0.25, 0.52) false
julia #(0.37, -0.248) false
julia #(0.5, 0.0) false
)
)
rollout pFIFS "PF IFS" width:300 height:682 (
button btn1 "Curl" pos:[10,6] width:64 height:20
button btn2 "Tree" pos:[83,6] width:64 height:20
button btn3 "Davis" pos:[154,6] width:64 height:20
button btn4 "Leaf" pos:[225,6] width:64 height:20
button btn5 "Binary" pos:[10,33] width:64 height:20
button btn6 "Coral" pos:[83,33] width:64 height:20
button btn7 "Crystal" pos:[154,33] width:64 height:20
button btn8 "Dragon" pos:[225,33] width:64 height:20
button btn9 "Fern" pos:[10,61] width:64 height:20
button btn10 "Floor" pos:[83,61] width:64 height:20
button btn11 "Koch" pos:[154,61] width:64 height:20
button btn12 "Spiral" pos:[225,61] width:64 height:20
button btn13 "Swirl" pos:[10,88] width:64 height:20
button btn14 "Sierpinski" pos:[83,88] width:64 height:20
button btn15 "Triangle" pos:[154,88] width:64 height:20
button btn16 "Zigzag" pos:[225,88] width:64 height:20
button btn17 "Koch2" pos:[10,115] width:64 height:20
button btn18 "Morph" pos:[83,115] width:64 height:20
button btn19 "Dragon_3" pos:[154,115] width:64 height:20
button btn20 "Eiffel_Tower" pos:[225,115] width:64 height:20
button btn21 "Lattice" pos:[10,140] width:64 height:20
button btn22 "Goblins" pos:[83,140] width:64 height:20
button btn23 "Web" pos:[154,140] width:64 height:20
button btn24 "Flake" pos:[225,140] width:64 height:20
button btn25 "Windy" pos:[10,165] width:64 height:20
button btn26 "Wilting" pos:[83,165] width:64 height:20
button btn27 "Twigs" pos:[154,165] width:64 height:20
button btn28 "Needle" pos:[225,165] width:64 height:20
button btn29 "Scales" pos:[10,192] width:64 height:20
button btn30 "Sinewy" pos:[83,192] width:64 height:20
button btn31 "Ball_45" pos:[154,192] width:64 height:20
button btn32 "Nautilus" pos:[225,192] width:64 height:20
button btn33 "Dendrit_1" pos:[10,217] width:64 height:20
button btn34 "Dendrit_2" pos:[83,217] width:64 height:20
button btn35 "Koch_curve" pos:[154,217] width:64 height:20
button btn36 "Leaf_3" pos:[225,217] width:64 height:20
button btn37 "Wolfs" pos:[10,243] width:64 height:20
button btn38 "Fir_2" pos:[83,243] width:64 height:20
button btn39 "Spiral_12" pos:[154,243] width:64 height:20
button btn40 "Talon" pos:[225,243] width:64 height:20
button btn41 "Spiral_19" pos:[10,269] width:64 height:20
button btn42 "Chain_2" pos:[83,269] width:64 height:20
button btn43 "Square" pos:[154,269] width:64 height:20
button btn44 "Seashell" pos:[225,269] width:64 height:20
button btn45 "Branch" pos:[10,295] width:64 height:20
button btn46 "Frog_paws" pos:[83,295] width:64 height:20
button btn47 "Wood" pos:[154,295] width:64 height:20
button btn48 "Spiral_14" pos:[225,295] width:64 height:20
button btn49 "Chess" pos:[10,320] width:64 height:20
button btn50 "Chain" pos:[83,320] width:64 height:20
button btn51 "Net" pos:[154,320] width:64 height:20
button btn52 "Spiral_16" pos:[225,320] width:64 height:20
button btn53 "Spiral_17" pos:[10,346] width:64 height:20
button btn54 "Spiral_18" pos:[83,346] width:64 height:20
button btn55 "Crystal_2" pos:[154,346] width:64 height:20
button btn56 "Koch_Curve_3" pos:[225,346] width:64 height:20
button btn57 "Tree_2" pos:[10,372] width:64 height:20
button btn58 "Arrow" pos:[83,372] width:64 height:20
button btn59 "Diamond_2" pos:[154,372] width:64 height:20
button btn60 "Fish" pos:[225,372] width:64 height:20
button btn61 "Mandelbrot I" pos:[10,397] width:64 height:20
button btn62 "Tree_3" pos:[83,397] width:64 height:20
button btn63 "Parachute" pos:[154,397] width:64 height:20
button btn64 "Sierpinsky_3" pos:[225,397] width:64 height:20
button btn65 "Jagged" pos:[10,422] width:64 height:20
button btn66 "Boxes" pos:[83,422] width:64 height:20
button btn67 "Shooter" pos:[154,422] width:64 height:20
button btn68 "A_n_flake" pos:[225,422] width:64 height:20
button btn69 "Pentagon_3" pos:[10,446] width:64 height:20
button btn70 "First_star" pos:[83,446] width:64 height:20
button btn71 "Zigzag0" pos:[154,446] width:64 height:20
button btn72 "Neuron" pos:[225,446] width:64 height:20
button btn73 "Break_4" pos:[10,471] width:64 height:20
button btn74 "Atilla" pos:[83,471] width:64 height:20
button btn75 "Corner_35" pos:[154,471] width:64 height:20
button btn76 "Stairway" pos:[225,471] width:64 height:20
button btn77 "Star_55" pos:[10,497] width:64 height:20
button btn78 "Tee_3x3" pos:[83,497] width:64 height:20
button btn79 "Spiral_54" pos:[154,497] width:64 height:20
button btn80 "Snowflake-D" pos:[225,497] width:64 height:20
button btn81 "Mountains 2" pos:[10,524] width:64 height:20
button btn82 "Kieswetter" pos:[83,524] width:64 height:20
button btn83 "-" pos:[154,524] width:64 height:20
button btn84 "-" pos:[225,524] width:64 height:20
button btn85 "Mandelbrot" pos:[10,549] width:64 height:20
button btn86 "Julia" pos:[83,549] width:64 height:20
button btn87 "Julia 2" pos:[154,549] width:64 height:20
button btn88 "-" pos:[225,549] width:64 height:20
button btn89 "-" pos:[10,575] width:64 height:20
button btn90 "-" pos:[83,575] width:64 height:20
button btn91 "-" pos:[154,575] width:64 height:20
button btn92 "-" pos:[225,575] width:64 height:20
button btn93 "-" pos:[10,602] width:64 height:20
button btn94 "-" pos:[83,602] width:64 height:20
button btn95 "-" pos:[154,602] width:64 height:20
button btn96 "-" pos:[225,602] width:64 height:20
button btn97 "-" pos:[10,628] width:64 height:20
button btn98 "-" pos:[83,628] width:64 height:20
button btn99 "-" pos:[154,628] width:64 height:20
button btn100 "-" pos:[225,628] width:64 height:20
button bAll "All" pos:[10,655] width:64 height:20
label lblAll "" pos:[83,660] width:100 height:18
on btn1 pressed do (showFrct 1)
on btn2 pressed do (showFrct 2)
on btn3 pressed do (showFrct 3)
on btn4 pressed do (showFrct 4)
on btn5 pressed do (showFrct 5)
on btn6 pressed do (showFrct 6)
on btn7 pressed do (showFrct 7)
on btn8 pressed do (showFrct 8)
on btn9 pressed do (showFrct 9)
on btn10 pressed do (showFrct 10)
on btn11 pressed do (showFrct 11)
on btn12 pressed do (showFrct 12)
on btn13 pressed do (showFrct 13)
on btn14 pressed do (showFrct 14)
on btn15 pressed do (showFrct 15)
on btn16 pressed do (showFrct 16)
on btn17 pressed do (showFrct 17)
on btn18 pressed do (showFrct 18)
on btn19 pressed do (showFrct 19)
on btn20 pressed do (showFrct 20)
on btn21 pressed do (showFrct 21)
on btn22 pressed do (showFrct 22)
on btn23 pressed do (showFrct 23)
on btn24 pressed do (showFrct 24)
on btn25 pressed do (showFrct 25)
on btn26 pressed do (showFrct 26)
on btn27 pressed do (showFrct 27)
on btn28 pressed do (showFrct 28)
on btn29 pressed do (showFrct 29)
on btn30 pressed do (showFrct 30)
on btn31 pressed do (showFrct 31)
on btn32 pressed do (showFrct 32)
on btn33 pressed do (showFrct 33)
on btn34 pressed do (showFrct 34)
on btn35 pressed do (showFrct 35)
on btn36 pressed do (showFrct 36)
on btn37 pressed do (showFrct 37)
on btn38 pressed do (showFrct 38)
on btn39 pressed do (showFrct 39)
on btn40 pressed do (showFrct 40)
on btn41 pressed do (showFrct 41)
on btn42 pressed do (showFrct 42)
on btn43 pressed do (showFrct 43)
on btn44 pressed do (showFrct 44)
on btn45 pressed do (showFrct 45)
on btn46 pressed do (showFrct 46)
on btn47 pressed do (showFrct 47)
on btn48 pressed do (showFrct 48)
on btn49 pressed do (showFrct 49)
on btn50 pressed do (showFrct 50)
on btn51 pressed do (showFrct 51)
on btn52 pressed do (showFrct 52)
on btn53 pressed do (showFrct 53)
on btn54 pressed do (showFrct 54)
on btn55 pressed do (showFrct 55)
on btn56 pressed do (showFrct 56)
on btn57 pressed do (showFrct 57)
on btn58 pressed do (showFrct 58)
on btn59 pressed do (showFrct 59)
on btn60 pressed do (showFrct 60)
on btn61 pressed do (showFrct 61)
on btn62 pressed do (showFrct 62)
on btn63 pressed do (showFrct 63)
on btn64 pressed do (showFrct 64)
on btn65 pressed do (showFrct 65)
on btn66 pressed do (showFrct 66)
on btn67 pressed do (showFrct 67)
on btn68 pressed do (showFrct 68)
on btn69 pressed do (showFrct 69)
on btn70 pressed do (showFrct 70)
on btn71 pressed do (showFrct 71)
on btn72 pressed do (showFrct 72)
on btn73 pressed do (showFrct 73)
on btn74 pressed do (showFrct 74)
on btn75 pressed do (showFrct 75)
on btn76 pressed do (showFrct 76)
on btn77 pressed do (showFrct 77)
on btn78 pressed do (showFrct 78)
on btn79 pressed do (showFrct 79)
on btn80 pressed do (showFrct 80)
on btn81 pressed do (showFrct 81)
on btn82 pressed do (showFrct 82)
on btn85 pressed do (mndlbrt 1)
on btn86 pressed do (julia #(-1.0, 0.0) true)
on btn87 pressed do (julia #(-0.2, 0.75) false)
on bAll pressed do (fAlPFFr false)
)
tSttngs 2 50 true false true false
shMsg = false
createDialog pFIFS 301 683 200 50 modal:on escapeEnable:on lockHeight:on lockWidth:on
На рис. 8 приведены два построенных из частиц СИФ-фрактала.
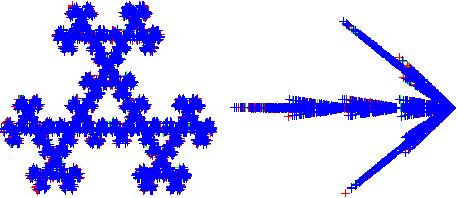
Рис. 8. СИФ-фракталы Flake и Arrow
Число вариантов реализации СИФ-изображения не ограничивается приведенными. Кроме того, в некоторых случаях можно управлять порядком вывода точек изображения, предварительно записав их координаты в массив. Далее массив можно отсортировать, например, по Y-координате и выполнить последовательный вывод отсортированных точек. Такой прием, в частности, употреблен в работе "Времена года. Осень" конкурса "Живая картина" для отображения растущего дерева.