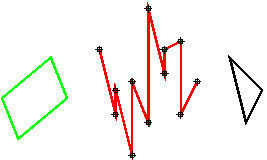
Рис. 3. Исходные фигуры и их сумма Минковского виде непересекающейся ломаной линии
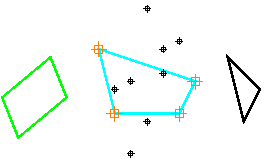
Рис. 4. Текущая ВО
Выпуклая оболочка конечного множества заданных на плоскости точек – это наименьший выпуклый многоугольник, содержащий все точки этого множества. При этом все вершины многоугольника – это точки исходного множества точек.
Потребность построения выпуклой оболочки возникла при решении задачи отображения суммы Минковского (рис. 1).
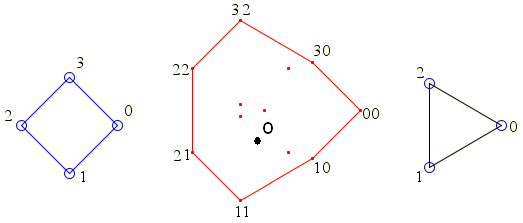
Рис. 1. Сумма Минковского вершин четырехугольника и треугольника. О – начало координат
Напомним, что суммой Минковского двух подмножеств A и B линейного пространства называется множество, состоящее из сумм всевозможных векторов из A и B:
A + B = {a + b: a ∈ A, b ∈ B}
Если A и B – это полигональные модели 3d-объектов или многоугольники, то a и b – это вершины геометрических фигур.
Выпуклая оболочка суммы Минковского показана на рис. 1 красным цветом. Вершины, эту оболочку образующие, пронумерованы. Вершины, находящиеся внутри оболочки, принадлежащие сумме Минковского, выведены без номеров.
Существует несколько алгоритмов построения выпуклой оболочки. Однако ввиду простоты задачи анализ этих алгоритмов не выполнялся, а был реализован достаточно очевидный алгоритм построения выпуклой оболочки конечного множества заданных на плоскости точек.
Не исключено, что такой алгоритм уже предложен. Если так, то в работу следует добавить ссылку на соответствующий источник.
Программа, реализующая рассматриваемый алгоритм, написана на MAXScript.
Алгоритм обеспечивает построения выпуклой оболочки конечного множества заданных на плоскости точек. Исходное множество точек содержится в массиве arrMS2. При иллюстрации алгоритма число точек исходного множества невелико. Вдобавок это множество определяется как сумма Минковского двух выпуклых фигур (рис. 2).
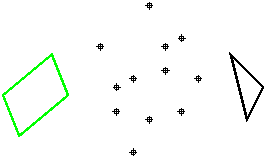
Рис. 2. Исходные фигуры и их сумма Минковского
При последующем тестировании алгоритма точки генерируются случайным образом.
Построение и отображение выпуклой оболочки (ВО) суммы Минковского выпуклых многоугольников выполним по следующему алгоритму:

Рис. 3. Исходные фигуры и их сумма Минковского виде непересекающейся ломаной линии

Рис. 4. Текущая ВО
Достроенная оболочка может оказаться невыпуклой (рис. 5), например, если A и B задаются следующими массивами:
arrNG = #([-40.0, 5.0, 0], [-50.0, -20.0, 0], [-70.0, 0.0, 0], [-50.0, 40.0, 0])
arrNG2 = #([45.0, 10.0, 0], [70.0, -10.0, 0], [60.0, 30.0, 0])
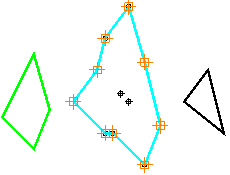
Рис. 5. Необходима корректировка оболочки
Эту ситуацию можно обрабатывать по ходу построения оболочки. Можно также выправить полученную невыпуклую оболочку (в примере осуществляется переход от фигуры, приведенной на рис. 5, к фигуре, показанной на рис. 6).
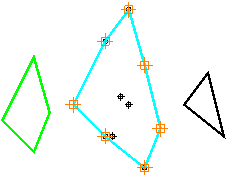
Рис. 6. После правки имеем выпуклую оболочку
При правке нужно взять вершины полученной оболочки через одну и посмотреть, как расположена находящаяся между ними вершина v. Если она в левой полуплоскости взятых вершин, то v удаляется из массива вершин выпуклой оболочки.
Такую правку следует выполнять до полного устранения проблемных вершин.
Пункту 3 приведенного алгоритма отвечает следующий код:
-- Оставляем на каждой линии x = const не более двух точек
arrMS2 = #()
cnt = arrMS.Count
k = 1
while k < cnt do (
x = arrMS[k][1]
arrMSX = #(arrMS[k])
k2 = k + 1
while k2 <= cnt and arrMS[k2][1] == x do (
append arrMSX arrMS[k2]
k2 += 1
)
cntX = k2 - k
if cntX > 2 do (
qsort arrMSX compareFN k:2
)
append arrMS2 arrMSX[1]
if cntX > 1 do append arrMS2 arrMSX[cntX]
k = k2
)
append arrMS2 arrMS[cnt]
В действительности этот пункт избыточен, поэтому итоговый код приведенный фрагмент не содержит.
Поскольку алгоритм предусматривает сортировку исходного множества вершин, то его вычислительная сложность равна O(nlogn).
Приводимая программа обеспечивает сначала построение оболочки, которая может быть и невыпуклой, а затем выполняет ее правку. Кроме того, выполняется визуализация обрабатываемых геометрических объектов. Так, вывод многоугольников и ломаной линии обеспечивает функция drwNG, а для вывода вершин употребляется объект Point.
-- Функция получает точки v0, v1 и v2
-- Возвращает
-- положительное число, если v2 находится слева от линии, проведенной через v0 и v1
-- 0, если v2 - на линии
-- отрицательное число, если v2 находится справа от линии
fn sLft v0 v1 v2 = (v1[1] - v0[1]) * (v2[2] - v0[2]) - (v2[1] - v0[1]) * (v1[2] - v0[2])
-- Функция рисует фигуру по массиву точек arrNG
fn drwNG arrNG ps clr fCls fPts = (
spln = line pos:ps wireColor:clr \
render_renderable:on render_displayRenderMesh:on \
render_thickness:1.0
addNewSpline spln
for k = 1 to arrNG.Count do (
addKnot spln 1 #corner #line arrNG[k]
if fPts do point pos:arrNG[k] size:10 drawOnTop:on box:on wireColor:orange
)
if fCls do close spln 1
updateShape spln
)
fn compareFN v1 v2 k:1 = (
local d = v1[k] - v2[k]
case of (
(d < 0.): -1
(d > 0.): 1
default: 0
)
)
fn cnvxHll arrMS2 = (
-- Сортируем точки по возрастанию их х-координаты
qsort arrMS2 compareFN k:1
-- Вывод ломаной линии
-- drwNG arrMS2 [0, 0, 0] (color 255 0 0) false true
-- Построение выпуклой оболочки
-- arrCnvxMS - массив вершин выпуклой оболочки
v1 = arrMS2[1]
v2 = arrMS2[2]
if arrMS2[1][2] < arrMS2[2][2] do (
v1 = v2
v2 = arrMS2[1]
)
cnt2 = arrMS2.Count
v3 = arrMS2[cnt2 - 1]
v4 = arrMS2[cnt2]
if arrMS2[cnt2 - 1][2] > arrMS2[cnt2][2] do (
v3 = v4
v4 = arrMS2[cnt2 - 1]
)
arrCnvxMS = #(v1, v2, v3, v4)
arrCtv = #(1, 4, 2, 3)
for k = 1 to 2 do deleteItem arrMS2 1
for k = 1 to 2 do deleteItem arrMS2 arrMS2.Count
--drwNG arrCnvxMS [0, 0, 0] (color 0 255 255) true true
-- Вывод вершин массива arrMS2
cnt2 = arrMS2.Count
for k = 1 to cnt2 do point pos:arrMS2[k] size:5 drawOnTop:on box:on wireColor:black
for k = 1 to cnt2 do (
v = arrMS2[k]
sd = sLft arrCnvxMS[arrCtv[1]] arrCnvxMS[arrCtv[2]] v
m = 0
if sd > 0 then
m = 1
else (
sd = sLft arrCnvxMS[arrCtv[3]] arrCnvxMS[arrCtv[4]] v
if sd < 0 do m = 4
)
if m > 0 do (
insertItem v arrCnvxMS arrCtv[m]
arrCtv[2] += 1
arrCtv[3] += 1
arrCtv[4] += 1
)
)
-- drwNG arrCnvxMS [0, 0, 0] (color 0 255 255) true true
-- Выправляем полученную оболочку
dltd = true
while dltd do (
dltd = false
k = 1
while k <= arrCnvxMS.Count do (
cnt = arrCnvxMS.Count
case k of (
cnt: (k2 = 2; k3 = 1)
(cnt - 1): (k2 = 1; k3 = cnt)
default: (k2 = k + 2; k3 = k + 1)
)
if sLft arrCnvxMS[k] arrCnvxMS[k2] arrCnvxMS[k3] > 0 then (
deleteItem arrCnvxMS k3
dltd = true
)
else
k += 1
)
)
return arrCnvxMS
)
delete $*
-- Массивы с координатами вершин исходных многоугольников
arrNG = #([-40.0, 5.0, 0], [-70.0, -20.0, 0], [-80.0, 5.0, 0], [-50.0, 30.0, 0])
arrNG2 = #([80.0, 10.0, 0], [70.0, -10.0, 0], [60.0, 30.0, 0])
--arrNG = #([-40.0, 5.0, 0], [-60.0, -15.0, 0], [-80.0, 5.0, 0], [-60.0, 25.0, 0])
--arrNG2 = #([80.0, 5.0, 0], [60.0, -15.0, 0], [60.0, 25.0, 0])
--arrNG = #([-40.0, 5.0, 0], [-50.0, -20.0, 0], [-70.0, 0.0, 0], [-50.0, 40.0, 0])
--arrNG2 = #([45.0, 10.0, 0], [70.0, -10.0, 0], [60.0, 30.0, 0])
-- Вывод исходных фигур
drwNG arrNG [0, 0, 0] (color 0 255 0) true false
drwNG arrNG2 [0, 0, 0] (color 0 0 0) true false
-- Массив с координатами вершин суммы Минковского
arrMS = #()
for k = 1 to arrNG.Count do (
pNG = arrNG[k]
for k2 = 1 to arrNG2.Count do
append arrMS (pNG + arrNG2[k2])
)
cnt = arrMS.Count
-- Вывод вершин массива arrMS
-- for k = 1 to cnt do point pos: arrMS[k] size:5 box:on wireColor:black
-- Получаем на базе массива arrMS непересекающуюся ломаную линию
arrMS2 = for k = 1 to cnt collect arrMS[k]
arrCnvxMS = cnvxHll arrMS2
drwNG arrCnvxMS [0, 0, 0] (color 0 255 255) true true
Программа, если исключить из подсчета комментарий и вспомогательный код, содержит менее 50 строчек кода, что говорит о сравнительной простоте рассматриваемой задачи.
При тестировании алгоритма исходное множество точек можно получить, применив следующий код:
-- Массив с координатами тестового множества вершин
-- Координаты точек задаем, употребляя датчик случайных чисел
n = 300
arrMS2 = for k = 1 to n collect (point3 (random -100.0 100.0) (random -50.0 150.0) 0)
-- Вывод вершин массива arrMS2
for k = 1 to arrMS2.Count do point pos:arrMS2[k] size:5 box:on wireColor:black
Результат одного из тестовых примеров показан на рис. 7.
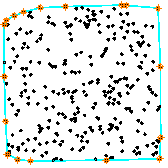
Рис. 7. Выпуклая оболочка множества, содержащего 300 точек