Список работ

Воспроизведение фракталов средствами стандартной графики Фортрана

Содержание

• Введение
• Снежинка Коха
• L-системы
• Системы итерированных функций
  • Введение в СИФ
  • Примеры СИФ
  • Морфинг СИФ
• Алгебраические фракталы
  • Множество Мандельброта
  • Множество Жюлиа
• Стохастические фракталы
• Литература

Введение

Задача получения навыков программирования на Фортране решается путем создания программ вывода фрактальных объектов, таких, как L-системы, СИФ, алгебраические и стохастические фракталы. Для запуска приводимых программ может быть использован любой компилятор, поддерживающий стандарт Фортран 90 или более поздние издания Фортрана.

Снежинка Коха

Правила получения фрактальной кривой Коха наглядно иллюстрирует рис. 1.

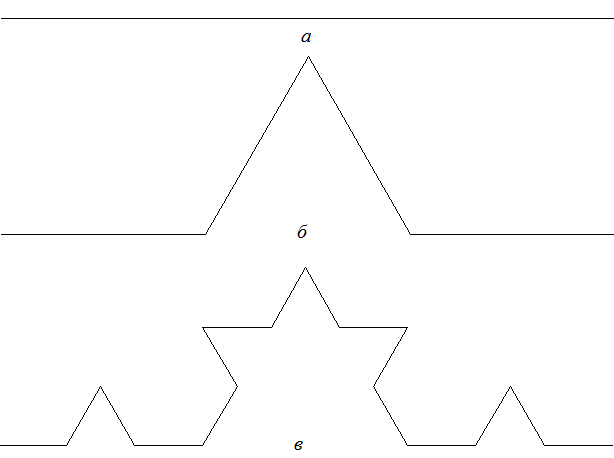
Рис. 1. Этапы получения кривой Коха: а - начальный отрезок (инициатор);б, в - второй и третий этапы построения кривой

При генерации кривой использован угол поворота, равный 60°. В принципе, угол можно задать и иным.

Код формирования и вывода кривой Коха на Фортране может быть таким:

module screen
 use ifqwin
 integer(4) rslt
 integer(2) XE, YE ! XE, YE - размеры экрана (в пикселях)
 integer(4), parameter :: nm = 10000 ! Предельное число вершин в кривой Коха
 real(8) rotd(2, 2) ! Матрица поворота против часовой стрелки
 real(8) kochN(nm, 2) ! Массив вершин кривой Коха на следующей итерации
end module screen
!
subroutine oneSide(nv, koch) ! Вывод кривой Коха
 use screen
 implicit none
 type(wxycoord) :: wt
 integer(4) :: i
 integer(4) nv ! Число вершин в кривой Коха
 real(8) koch(nm, 2) ! Массив вершин кривой Коха
 call moveto_w(koch(1, 1), koch(1, 2), wt)
 do i = 2, nv
  rslt = lineto_w(koch(i, 1), koch(i, 2))
 end do
end subroutine oneSide
!
subroutine newKoch(nv, koch) ! Формирует кривую Коха на очередном шаге
 use screen
 implicit none
 integer(4) j, j2
 real(8) x, y ! Координаты начала разбиваемого отрезка
 real(8) dx, dy, x2, y2
 integer(4) nv ! Число вершин в кривой Коха
 real(8) koch(nm, 2) ! Массив вершин кривой Коха
 j2 = 0
 do j = 1, nv - 1
  x = koch(j, 1)
  y = koch(j, 2)
  ! Разбиваем текущий отрезок на 3 части
  dx = (koch(j + 1, 1) - x) / 3.0_8
  dy = (koch(j + 1, 2) - y) / 3.0_8
  x2 = x + dx
  y2 = y + dy
  j2 = j2 + 1
  kochN(j2, :) = (/ x, y /)
  j2 = j2 + 1
  kochN(j2, :) = (/ x2, y2 /)
  ! Формируем выступ
  j2 = j2 + 1
  kochN(j2, :) = (/ x2, y2 /) + matmul((/ dx, dy /), rotd)
  j2 = j2 + 1
  kochN(j2, :) = (/ x2 + dx, y2 + dy /)
 end do
 j2 = j2 + 1
 kochN(j2, :) = koch(nv, :)
 nv = j2
 koch = kochN
 call oneSide(nv, koch) ! Графический вывод кривой Коха
end subroutine newKoch
!
program kochCurv ! Фрактальная кривая Коха
 use screen
 implicit none
 integer(2) kv
 integer(4) i
 type(windowconfig) wc
 real(8) :: cd, sd ! Косинус и синус угла поворота
 integer(4) nv ! Число вершин в кривой Коха
 real(8) koch(nm, 2) ! Массив вершин кривой Коха
 cd = cosd(60.0_8)
 sd = sind(60.0_8)
 ! Матрица поворота на 60 градусов по часовой стрелке
 rotd = reshape((/ cd, sd, -sd, cd /), shape = (/ 2, 2 /))
 rslt = setbkcolorrgb(#ffffff) ! Белый цвет фона
 call clearscreen($gclearscreen) ! Заливка экрана цветом фона
 rslt = getwindowconfig(wc)
 XE = wc.numxpixels; YE = wc.numypixels ! Число пикселей по осям X и Y
 kv = 5 ! Задаем видовой порт в центре окна вывода
 call setviewport(XE / kv, YE / kv, (kv - 1_2) * XE / kv, (kv - 1_2) * YE / kv)
 ! Работаем в оконной системе координат с двойной точностью
 rslt = setcolor(0) ! Текущий цвет - черный
 ! Задаем инициатор
 koch(1, :) = (/ 1.0_8, YE / 1.9_8 /)
 koch(2, :) = (/ XE - 1.0_8, YE / 1.9_8 /)
 nv = 2 ! Начальное число вершин в кривой Коха
 ! Вывод начального отрезка (инициатора)
 call oneSide(nv, koch)
 read * ! Ожидаем нажатия Enter
 do i = 1, 4
  ! Вывод новой ситуации
  call clearscreen($gclearscreen) ! Заливка экрана цветом фона
  call newKoch(nv, koch)
  read * ! Ожидаем нажатия Enter
 end do
end program kochCurv

В программе использована стандартная графика Фортрана и двойная точность для вещественных данных. Полагается, что в процессе вычислений число вершин nv получаемой кривой не превышает заданного в модуле screen значения nm.

После выполнения четвертого шага кривая Коха приобретает представленный на рис. 2 вид.

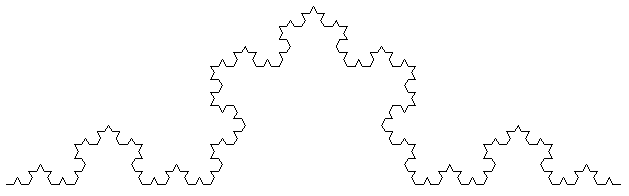
Рис. 2. Кривая Коха после четырех итераций

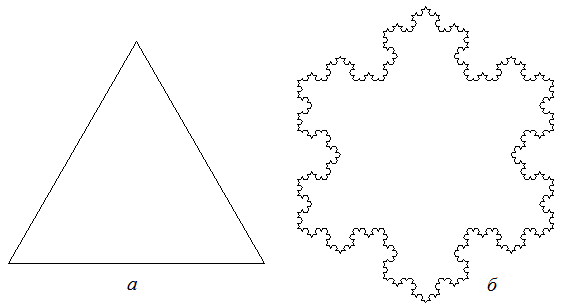
Выполнив построение кривой Коха, для каждой из сторон заданного треугольника (рис. 3, а) (или иного многоугольника), мы получим так называемую снежинку Коха (рис. 3, б).

Рис. 3. Снежинка Коха: а - инициаторы; б - снежинка Коха после четырех итераций

Приведем код получения снежинки (большая часть кода заимствована из вышеприведенной программы kochCurv).

program kochSnowPiece ! Снежинка Коха
 use screen ! Код модуля см. выше
 implicit none
 integer(2) :: kv
 integer(4) :: n, i
 integer(4) :: nv1, nv2, nv3
 type(windowconfig) wc
 real(8) :: koch1(nm, 2) ! Массивы вершин снежинки Коха
 real(8) :: koch2(nm, 2)
 real(8) :: koch3(nm, 2)
 real(8) :: cd, sd ! Косинус и синус угла поворота
 rslt = setbkcolorrgb(#ffffff) ! Белый цвет фона
 call clearscreen($gclearscreen) ! Заливка экрана цветом фона
 rslt = getwindowconfig(wc)
 XE = wc.numxpixels; YE = wc.numypixels ! Число пикселей по осям X и Y
 kv = 3 ! Задаем видовой порт в центре окна вывода
 call setviewport(XE / kv, YE / kv, (kv - 1_2) * XE / kv, (kv - 1_2) * YE / kv)
 ! Работаем в оконной системе координат с двойной точностью
 rslt = setcolor(0) ! Текущий свет - черный
 cd = cosd(60.0_8); sd = sind(60.0_8)
 ! Матрица поворота на 60 градусов по часовой стрелке
 rotd = reshape((/ cd, sd, -sd, cd /), shape = (/ 2, 2 /))
 ! Задаем инициаторы - стороны приведенного на рис. 3, а треугольника
 koch1(1, 1) = XE / kv; koch1(1, 2) = (kv - 1) * YE / kv
 koch1(2, 1) = (kv - 1) * XE / kv; koch1(2, 2) = koch1(1, 2)
 koch2 = koch1
 koch2(2, :) = koch1(1, :) + matmul(koch1(2, :) - koch1(1, :), rotd)
 koch3(1, :) = koch2(2, :); koch3(2, :) = koch1(2, :)
 nv1 = 2; nv2 = 2; nv3 = 2
 ! Вывод начального треугольника (инициаторов)
 do n = 1, 3
  call oneSide(nv1, koch1) ! Вывод одной стороны треугольника
  call oneSide(nv2, koch2) ! Код подпрограммы oneSide см. выше
  call oneSide(nv3, koch3)
 end do
 read * ! Ожидаем нажатия Enter
 do i = 1, 4
  ! Вывод новой ситуации
  call clearscreen($gclearscreen) ! Заливка экрана цветом фона
  ! Матрица поворота на 60 градусов против часовой стрелки
  rotd = reshape((/ cd, -sd, sd, cd /), shape = (/ 2, 2 /))
  call newKoch(nv1, koch1) ! Код подпрограммы newKoch см. выше
  ! Матрица поворота на 60 градусов по часовой стрелке
  rotd = reshape((/ cd, sd, -sd, cd /), shape = (/ 2, 2 /))
  call newKoch(nv2, koch2)
  call newKoch(nv3, koch3)
  read * ! Ожидаем нажатия Enter
 end do
end program kochSnowPiece

Подпрограммы oneSide и newKoch, вызываемые главной программой kochSnowPiece, а также модуль screen мы берем из вышеприведенной программы вывода кривой Коха. Как и ранее, полагается, что в процессе вычислений число вершин nv1, nv2 и nv3 получаемой снежинки не превышает заданного в модуле screen значения nm.

L-системы

Инициатор и выполняемые с ним преобразования можно записать на языке L-систем. Так, только что выведенная кривая Коха описывается на этом языке следующим образом:

Кривая Коха {
θ = 60; ! Угол поворота равен 60°
F; ! Аксиома (инициатор в виде отрезка) (F - вперед)
F = F-F++F-F; ! Правило преобразования отрезка
}

В правиле преобразования отрезка знаки - и + означают соответственно поворот против и по часовой стрелке на угол θ

Рассмотрим язык L-систем более детально.

Для графической реализации L-систем используется так называемая черепашья графика. При этом исполнитель (черепашка) может вспомнить лишь то, что запомнил в последний раз. Исполнитель движется по плоскости дискретными шагами, как правило, прочерчивая свой след, но при необходимости может перемещаться и без рисования.

Текущее состояние черепашки описывается набором из трех параметров (х, у, α), где

• (х, у) - текущие координаты черепашки;
• α - угол, определяющий направление, в котором черепашка ползет по команде "вперед".
• Начальное состояние черепашки описывается набором из пяти параметров: (х₀, y₀, α₀, step, θ), где
• х₀, y₀, α₀ - начальные значения координат и угла;
• step - длина одного шага черепашки, который она делает по команде F ("вперед");
• θ - угол поворота; определяет, на сколько поворачивается черепашка, то есть на сколько меняется угол а при выполнении команд - ("налево") и + ("направо").

Черепашка выполняет последовательность команд, задаваемых кодовым словом, символы которого читаются слева направо. Кодовое слово может включать следующие символы:

• F - переместиться вперед на шаг step в направлении α, прорисовывая след (отрезок);
• b - переместиться вперед на шаг step в направлении α, не прорисовывая след;
• [ - открыть ветвь, то есть сохранить в конце стека текущее состояние (х, у, α);
• ] - закрыть ветвь, то есть взять из стека и присвоить переменным (х, у, α) последнее запомненное в стеке состояние;
• + - повернуться направо (по часовой стрелке) на угол θ (при исполнении этой команды меняется только угол α);
• - - повернуться налево (против часовой стрелки) на угол θ (при исполнении этой команды также меняется только угол α).

Формально детерминированная L-система состоит из алфавита, слова инициализации, называемого аксиомой, или инициатором, и набора порождающих правил, указывающих, как следует преобразовывать слово при переходе от одной итерации к следующей.

L-система, соответствующая снежинке Коха (рис. 3, б), имеет то же порождающее правило, что и L-система для кривой Коха, но иную, задающую равносторонний (рис. 3, а) треугольник аксиому.

Снежинка Коха {
θ = 60; ! Угол поворота равен 60°
F++F++F; ! Аксиома (равносторонний треугольник)
F = F-F++F-F; ! Порождающее правило
}

На каждом шаге каждая буква F заменяется на порождающее правило и в результате получается снежинка Коха.

Программа, выводящая L-систему, будет рассмотрена ниже. Для вывода снежинки Коха в модуле screen этой программы указываются следующие заменяемые параметры:

 ! Заменяемые параметры
 real(8), parameter :: dNgl = 60.0_8 ! Приращение угла поворота
 real(8) :: strtPnt(2) = (/ 400.0_8, 700.0_8 /) ! Начальная точка
 real(8) :: stp(2) = (/9.0_8, 0.0_8 /) ! Координаты конца шага, расположенного в начале координат
 character(nRl) :: xm = 'F++F++F' ! Аксиома
 character(nRl) :: rlF = 'F-F++F-F' ! Исходное правило
 character(nRl) :: rlB = '' ! Исходное b-правило
 integer(4), parameter :: nStp = 4 ! Число итераций

Снежинка Коха не имеет разрывов, и черепашка при движении каждый раз прорисовывает свой след. Разрывные образы получаются, если порождающее правило содержит символ b. Так, используя этот символ, можно задать, например, следующую L-систему:

Цепочка (рис. 4) {
θ = 90; ! Угол поворота равен 90°
F+F+F+F; ! Аксиома (квадрат)
F = F+b-F-FFF+F+b-F; ! Порождающие правила
b = bbb;
}

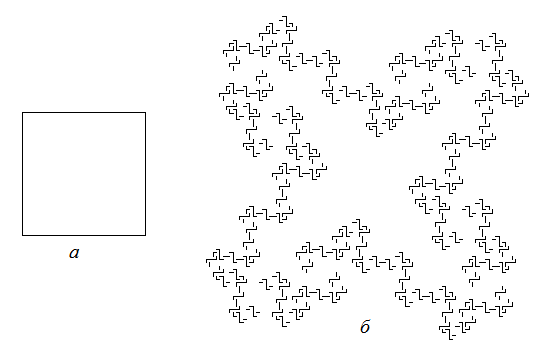
Рис. 4. Цепочка: а - инициатор; б - цепочка после трех итераций

Используем для построения цепочки следующий код:

module screen
 use ifqwin
 integer(4) rslt
 character(1) s
 integer(2) XE, YE ! XE, YE - размеры экрана (в пикселях)
 integer(4), parameter :: nm = 100000 ! Предельное число элементов в массиве символов правила
 real(8) rotd(2, 2) ! Матрица поворота
 character(1) frctl(nm) ! Массив символов, образующих правило
 character(1) frctlN(nm) ! Массив символов, образующих правило на следующей итерации
 integer(4) nFrctl ! Число символов в исполняемом правиле
 integer(4) nSRF ! Число символов в исходном F-правиле
 integer(4) nSRB ! Число символов в исходном b-правиле
 integer(4), parameter :: nRl = 200 ! Предельное число символов в исходном правиле и аксиоме
 character(1) :: sRlF(nRl) ! Массив символов исходного F-правила
 character(1) :: sRlB(nRl) ! Массив символов исходного b-правила
 ! Заменяемые параметры
 real(8), parameter :: dNgl = 90.0_8 ! Приращение угла поворота
 real(8) :: strtPnt(2) = (/ 1200.0_8, 300.0_8 /) ! Начальная точка
 real(8) :: stp(2) = (/0.0_8, 6.0_8 /) ! Координаты конца шага, расположенного в начале координат
 character(nRl) :: xm = 'F+F+F+F' ! Аксиома
 character(nRl) :: rlF = 'F+b-F-FFF+F+b-F' ! Исходное F-правило
 character(nRl) :: rlB = 'bbb' ! Исходное b-правило
 integer(4), parameter :: nStp = 3 ! Число итераций
end module screen
!
subroutine mkRotd(ngl, rotd) ! Формирование матрицы поворота
 real(8) ngl
 real(8) cd, sd ! Косинус и синус угла поворота
 real(8) rotd(2, 2)
 cd = cosd(ngl)
 sd = sind(ngl)
 ! Матрица поворота на угол ngl по часовой стрелке
 rotd = reshape((/ cd, sd, -sd, cd /), shape = (/ 2, 2 /))
end subroutine mkRotd
!
subroutine mkFrctl() ! Формирование исполняемого правила
 use screen
 integer(4) k, k2, j
 j = 0
 do k = 1, nFrctl
  s = frctl(k)
  select case(s)
  case('F')
   do k2 = 1, nSRF
    j = j + 1
    frctlN(j) = sRlF(k2)
   end do
  case('b')
   do k2 = 1, nSRB
    j = j + 1
    frctlN(j) = sRlB(k2)
   end do
  case('+', '-', '[', ']')
   j = j + 1
   frctlN(j) = s
  end select
 end do
 frctl = frctlN
 nFrctl = j
end subroutine mkFrctl
!
subroutine mkRR(strng, rr, nRr) ! Формирует массив символов rr по строке символов strng
 implicit none
 character(*) strng
 character(1) rr(*), s
 integer(4) k, nRr
 nRr = 0
 do k = 1, len_trim(strng)
  s = strng(k:k)
  if (s /= ' ') then
   nRr = nRr + 1
   rr(nRr) = s
  end if
 end do
end subroutine mkRR
!
program doFrctl
 use screen
 implicit none
 integer(2) kv
 integer(4) k
 type(windowconfig) wc
 rslt = setbkcolorrgb(#ffffff) ! Белый цвет фона
 rslt = getwindowconfig(wc)
 XE = wc.numxpixels; YE = wc.numypixels ! Число пикселей по осям X и Y
 kv = 5 ! Задаем видовой порт в центре окна вывода
 call setviewport(XE / kv, YE / kv, (kv - 1_2) * XE / kv, (kv - 1_2) * YE / kv)
 ! Работаем в оконной системе координат с двойной точностью
 rslt = setcolor(0) ! Текущий цвет - черный
 ! Массив символов исходного F-правила
 call mkRR(rlF, sRlF, nSRF)
 ! Массив символов исходного b-правила
 call mkRR(rlB, sRlB, nSRB)
 ! Аксиома
 call mkRR(xm, frctl, nFrctl)
 do k = 1, nStp
  ! Вывод новой ситуации
  call clearscreen($gclearscreen) ! Заливка экрана цветом фона
  call mkFrctl() ! Формируем массив символов текущего правила
  call pltFrctl() ! Вывод фрактала
  read * ! Ожидаем нажатия Enter
 end do
end program doFrctl
!
subroutine pltFrctl() ! Вывод фрактала
 use screen
 implicit none
 type(wxycoord) wt
 integer(4) k, nStck
 real(8) pnt(2), stck(nm, 3)
 real(8) ngl ! Угол поворота
 logical(4) rt
 call clearscreen($gclearscreen) ! Заливка экрана цветом фона
 call moveto_w(strtPnt(1), strtPnt(2), wt)
 pnt = strtPnt
 nStck = 0
 ngl = 0.0_8
 do k = 1, nFrctl
  s = frctl(k)
  select case(s)
  case('+')
   ngl = ngl + dNgl
  case('-')
   ngl = ngl - dNgl
  case('[')
   nStck = nStck + 1
   stck(nStck, 1:2) = pnt
   stck(nStck, 3) = ngl
  case(']')
   pnt = stck(nStck, 1:2)
   ngl = stck(nStck, 3)
   nStck = nStck - 1
   call moveto_w(pnt(1), pnt(2), wt)
  case('F', 'b')
   call mkRotd(ngl, rotd)
   pnt = pnt + matmul(stp, rotd)
   if (s == 'F') then
    rslt = lineto_w(pnt(1), pnt(2))
   else
    call moveto_w(pnt(1), pnt(2), wt)
   end if
  end select
 end do
end subroutine pltFrctl

Символы [ и ] позволяют создавать ветвления. Когда встречается символ [ (открыть ветвь), то запоминается положение в направлении черепашки, то есть переменные (x, y, α), и возврат к этим установкам происходит позднее, когда встречается символ ] закрытия соответствующей ветви. Для хранения триплетов (x, y, α) можно использовать стек

При работе со стеком используется принцип LIFO (last in, first out).
Новые данные записываются в конец стека. Когда ветвь закрывается, переменным (x, y, ) присваиваются значения, считанные из конца стека. Затем эти значения из стека удаляются.

На приведенных ниже рис. 5 и 6 представлены фрактальные кривые, напоминающие растения, построенные с использованием L-систем, имеющих операции ветвления.

Рис. 5. Куст после четырех итераций

L-система для рис. 5:

Куст {
θ = 22.5; ! Угол поворота равен 22.5°
F; ! Аксиома (отрезок)
F = FF+[+F-F-F]-[-F+F+F]; ! Порождающее правило
}

Куст выводится, если в модуле screen программы, использованной для вывода цепочки, задать следующие заменяемые параметры:

 ! Заменяемые параметры
 real(8), parameter :: dNgl = 22.5_8 ! Приращение угла поворота
 real(8) :: strtPnt(2) = (/ 400.0_8, 800.0_8 /) ! Начальная точка
 real(8) :: stp(2) = (/0.0_8, -10.0_8 /) ! Координаты конца шага, расположенного в начале координат
 character(nRl) :: xm = 'F' ! Аксиома
 character(nRl) :: rlF = 'FF+[+F-F-F]-[-F+F+F]' ! Исходное правило
 character(nRl) :: rlB = '' ! Исходное b-правило
 integer(4), parameter :: nStp = 4 ! Число итераций

Рис. 6. Цветок после четырех итераций

L-система для рис. 6:

Цветок {
θ = π/16; ! Угол поворота
F[+F+F][-F-F][++F][--F]F; ! Аксиома
F = FF[++F][+F][F][-F][--F]; ! Порождающее правило
}

Параметры для выводя цветка:

 ! Заменяемые параметры
 real(8), parameter :: dNgl = 11.25_8 ! Приращение угла поворота
 real(8) :: strtPnt(2) = (/ 400.0_8, 800.0_8 /) ! Начальная точка
 real(8) :: stp(2) = (/0.0_8, -10.0_8 /) ! Координаты конца шага, расположенного в начале координат
 character(nRl) :: xm = 'F[+F+F][-F-F][++F][--F]F' ! Аксиома
 character(nRl) :: rlF = 'FF[++F][+F][F][-F][--F]' ! Исходное правило
 character(nRl) :: rlB = '' ! Исходное b-правило
 integer(4), parameter :: nStp = 4 ! Число итераций

Для генерации рис. 7, помимо операций ветвления, в L-систему введены вспомогательные переменные и соответствующие им порождающие правила.

Рис. 7. Ель после 11 итераций

L-система для рис. 7:

Ель {
θ = π/10; ! Угол поворота
SLFFF; ! Аксиома
G = +H[-G]L; ! Порождающие правила
H = -G[+H]L;
F = FF[++F][+F][F][-F][--F];
L = [-FFF][+FFF]F;
S = [+++G ][---G]TS;
T = TL;
}

Для вывода ели необходима доработка вышеприведенной программы отображения L-систем.

L-системы генерируют предфракталы заданного порядка. Собственно фракталы дают рассматриваемы ниже системы итерированных функций.

Системы итерированных функций

Введение в СИФ

Система итерированных функций (СИФ) - это совокупность аффинных преобразований. (Напомним, что произвольное преобразование координат можно выполнить, применив суперпозицию масштабирования, поворота, параллельного переноса и зеркального отображения координат.) В СИФ применяются сжимающие аффинные преобразования, то есть такие, в которых коэффициент масштабирования меньше единицы.

Рассмотрим построение кривой Коха с использованием аффинных преобразований. Каждый новый элемент кривой содержит четыре звена, полученных из образующего элемента использованием масштабирования, поворота и переноса.

1. Первое звено получается в результате сжатия исходного отрезка в 3 раза.
2. Второе звено строится с использованием всех имеющихся аффинных преобразований, а именно: сжатие в 3 раза, поворот на -60° и параллельный перенос на 1/3 длины исходного отрезка по оси X.
3. Третье звено строится аналогично второму: сжатие в три раза, поворот на +60°, параллельный перенос на 2/3 длины исходного отрезка по оси X.
4. Последнее звено: сжатие в три раза, параллельный перенос на 2/3 длины исходного отрезка по оси X.

Перечисленные правила построения кривой Коха позволяют найти СИФ, пригодную для построения этой кривой. Новые координаты x', y' точки x, y определяются следующими равенствами:

x' = a x + b y + e,
y' = c x + d y + f,

где

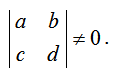
Поворот на угол φ против часовой стрелки описывается соотношениями

x' = x cosφ - y sinφ,
y' = x sinφ + y cosφ.

Растяжение (сжатие) задается уравнениями

x' = a x,
y' = b y.

Отражение относительно оси абсцисс задается формулами

x' = x,
y' = -y.

В результате переноса координаты меняются следующим образом:

x' = x + e,
y' = y + f.

Таким образом, коэффициенты преобразования координат для кривой Коха будут такими:

• для первого звена (сжатие в 3 раза)
    a = 1/3, b = 0, e = 0,
    c = 0, d = 1/3, f = 0;
• для второго звена (сжатие в 3 раза, поворот на -60° и параллельный перенос на 1/3 длины исходного отрезка по оси X)
    a = 1/3 * cos60, b = -1/3 * sin60, e = 1/3,
    c = 1/3 * sin60, d = 1/3 * cos60, f = 0;
• для третьего звена (сжатие в 3 раза, поворот на 60° и параллельный перенос на 2/3 длины исходного отрезка по оси X)
    a = -1/3 * cos60, b = 1/3 * sin60, e = 2/3,
    c = 1/3 * sin60, d = 1/3 * cos60, f = 0;
• для четвертого звена (сжатие в 3 раза, и параллельный перенос на 2/3 длины исходного отрезка по оси X)
    a = 1/3, b = 0, e = 2/3,
    c = 0, d = 1/3, f = 0.

Разместим вычисленные коэффициенты аффинных преобразований в табл. 1, добавив в нее столбец g.

Табл. 1.Коэффициенты аффинных преобразований элемента кривой Коха

Значения в столбце g пропорциональны площади, занимаемой каждым звеном (ширина звена принимается равной 1.0). Сумма значений ячеек столбца g равна единице. В нашем случае все звенья равновелики, поэтому элементы последнего столбца совпадают.
При построении СИФ значение в ячейке столбца g интерпретируется как вероятность выбора соответствующего аффинного преобразования из набора преобразований СИФ.
Совокупность приведенных в табл. 1 коэффициентов образует СИФ кривой Коха.

СИФ-кривая Коха строится по алгоритму 1.

Алгоритм 1:

1. Выбрать начальную точку изображения и вывести в выбранной точке пиксель.
2. Выбрать случайным образом одно из преобразований СИФ (в нашем случае одну из строчек табл. 1), найти координаты новой точки и вывести в ней пиксель изображения.
3. Повторить пункт 2 заданное число раз.

Начальная точка выбирается алгоритмом 2. Он обеспечивает выбор начальной точки в так называемом аттракторе, то есть области, принадлежащей изображению фрактала. Тогда все последующие точки блуждают в области аттрактора, не выходя за его пределы.

Алгоритм 2:

1. Выбрать произвольную точку окна вывода.
2. Применить к ней случайным образом выбранное преобразование СИФ.
3. Выполнить пункт 2 заданное число раз (например 100).

Рассматривая каждое преобразование в отдельности, можем заметить, что где бы мы ни начинали, после нескольких итераций, точка перестанет двигаться по экрану. Точка остановки называется неподвижной точкой.
Неподвижная точка каждого преобразования входит в состав аттрактора. Поэтому за начальную точку при построении фрактала можно взять, например, неподвижную точку первого преобразования из набора СИФ (взамен точки, найденной алгоритмом 2).
Чтобы порождаемые алгоритмом 1 точки окрашивали новые пиксели изображения, а не блуждала по старым, используют седьмой параметр, который представляет собой вероятность появления конкретного аффинного преобразования из набора преобразований СИФ.
На рис. 8 изображена кривая Кох, построенная преобразованиями СИФ.

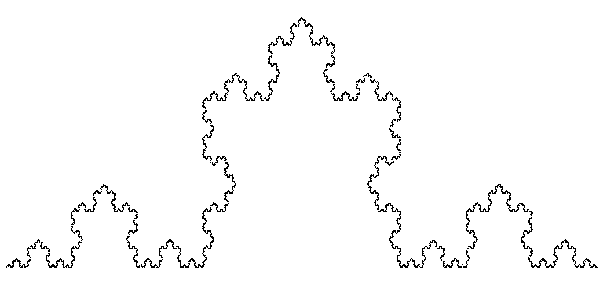
Рис. 8. СИФ-кривая Коха

Для ее вывода использована следующая программа.

module screen2
 ! minx, miny - минимальные мировые координаты изображения
 ! maxx, maxy - максимальные мировые координаты изображения
 ! Значения переменных minx, miny, maxx, maxy находит подпрограмма fconv
 real(8) :: minx, miny, maxx, maxy
 integer(2) :: rslt, XE, YE ! Размеры экрана (в пикселях)
 integer(4), parameter :: nm = 10000 ! Число выводимых точек
 integer(4), parameter :: nc = 28 ! Размер массива СИФ-коэффициентов
end module screen2
!
subroutine initGraph() ! Инициализация графического режима
 use ifqwin
 use screen2
 type(windowconfig) wc
 rslt = setbkcolorrgb(#ffffff) ! Белый цвет фона
 call clearscreen($gclearscreen) ! Заливка экрана цветом фона
 rslt = getwindowconfig(wc)
 XE = wc.numypixels; YE = wc.numypixels ! Число пикселей по осям Х и Y
 ! Задаем видовой порт
 call setviewport(10, 10, XE / 2_2, YE / 4_2)
 ! Работаем в оконной системе координат с двойной точностью
 rslt = setcolor(0) ! Текущий свет - черный
end subroutine initGraph
!
subroutine affine(x, y, ifs) ! Аффинные преобразования координат
 real(8) :: x, y, ifs(6), x2 ! Используем некоторое преобразование СИФ
 x2 = x * ifs(1) + y * ifs(2) + ifs(5)
 y = x * ifs(3) + y * ifs(4) + ifs(6)
 x = x2
end subroutine affine
!
subroutine spoint(ifs, x, y) ! Нахождение неподвижной точки
 real(8) :: ifs(6), x, y
 integer(4) :: i
 x = 1.0; y = 1.0 ! Произвольная точка плоскости
 do i = 1, 100 ! Используем первое преобразование СИФ
  call affine(x, y, ifs) ! для поиска начальной точки
 end do
end subroutine spoint
!
subroutine findk12(col, n, k1, k2)
 use screen2
 integer(4) :: n, j, k1, k2
 real(8) :: col(nc)
 real(4) :: p, r ! r - число, возвращаемое датчиком случайных чисел
 call random(r)
 p = 0.0
 do j = 1, n - 1 ! Выбираем случайным образом с учетом
  p = p + col(7 * j) ! столбца g очередное преобразование СИФ
  if(r <= p) exit
 end do
 k1 = 7 * (j - 1) + 1; k2 = k1 + 5
end subroutine findk12
!
! Находит простым перебором minx, miny, maxx, maxy
! minx, miny - диапазоны изменения мировых координат изображения
! maxx, maxy - максимальные мировые координаты изображения
subroutine fconv(ifs, n)
 use screen2
 integer(4) :: n, i, k1, k2
 real(8) :: ifs(nc), col(nc)
 real(8) :: x, y ! x, y - мировые координаты точки изображения
 maxx = -1.0e10; minx = 1.0e10
 maxy = -1.0e10; miny = 1.0e10
 call spoint(ifs(1:6), x, y) ! Ищем начальную точку
 ! Полностью воспроизводим цикл генерации изображения
 do i = 1, nm
  col = ifs ! Сохраняем коэффициенты СИФ,
  call findk12(col, n, k1, k2) ! Выбор преобразования СИФ
  call affine(x, y, col(k1:k2)) ! Вычисляем новые координаты точки
  ! Корректируем наши представления о максимальных и минимальных координатах образа
  maxx = max(x, maxx); minx = min(x, minx)
  maxy = max(y, maxy); miny = min(y, miny)
 end do
end subroutine fconv
! 
subroutine render(ifs, n) ! Вывод СИФ (выводится nm точек)
 use ifqwin
 use screen2
 integer(4) :: n, i, k1, k2
 real(8) :: ifs(nc), col(nc)
 real(8) :: x, y ! x, y - мировые координаты точки изображения
 logical(2) :: finv = .true.
 ! Задаем оконную систему координат, указывая диапазон изменения x и y
 rslt = setwindow(finv, minx, miny, maxx, maxy)
 call clearscreen($gclearscreen) ! Очистка экрана
 call spoint(ifs(1:6), x, y) ! Поиск начальной точки
 do i = 1, nm ! Вывод nm точек изображения
  col = ifs ! Сохраняем коэффициенты СИФ,
  call findk12(col, n, k1, k2) ! Выбор преобразования СИФ
  call affine(x, y, col(k1:k2)) ! Вычисляем новые координаты точки
  rslt = setpixel_w(x, y) ! Выводим очередную точку изображения
 end do
end subroutine render
!
program koch ! Вывод СИФ-изображения снежинки Коха
 use screen2
 real(8) :: ifs(nc)
 integer(4) :: n = 4 ! n - число преобразований СИФ
 call initGraph() ! Инициализация графического режима
 ! Задаем СИФ-кривую Коха
 ifs = (/  0.3333, 0.0, 0.0, 0.3333, 0.0, 0.0, 0.25, &
  0.1667, -0.2887, 0.2887, 0.1667, 0.3333, 0.0, 0.25, &
  -0.1667, 0.2887, 0.2887, 0.1667, 0.6666, 0.0, 0.25, &
  0.3333, 0.0, 0.0, 0.3333, 0.6666, 0.0, 0.25 /)
 call fconv(ifs, n) ! Поиск minx, miny, maxx, maxy
 call render(ifs, n) ! Вывод изображения (nm точек)
end program koch

В этой программе реализованы вышеприведенные алгоритмы 1 и 2. Для поиска коэффициентов перевода мировых координат в оконные и минимальных значений мировых координат применяется подпрограмма fconv. Она основана на следующем алгоритме.

Алгоритм 3:

1. Найти начальную точку, применив алгоритм 2.
2. Рассчитать мировые координаты всех точек будущего изображения и найти их минимальные (minx, miny) и максимальные значения (maxx, maxy).
3. Коэффициенты перевода мировых координат в оконные вычислить по формулам
   kwx = XE / (maxx - minx) ! Коэффициенты преобразования мировых координат точки в оконные
   kwy = YE / (maxy - miny),
   в которых XE и YE - размеры экрана.

Примеры СИФ

Приведем некоторые СИФ и соответствующие им изображения, а также программу их вывода. СИФ запишем в файл frctls.txt, предварив каждый СИФ соответствующим заголовком.

Состав файла fract.txt:

Иные СИФ-фракталы можно найти в работе Две реализации системы итерируемых функций.

Программа fract вывода образов, порождаемых СИФ, берет основные процедуры (initGraph, findk12, foncv, spoint, affine, render) и модуль screen2 из ранее приведенной программы koch.
Новая функция loadifs вводит в массив ifs заданный СИФ.

program fract
 use ifqwin
 use screen2
 implicit none
 real(8) :: ifs(nc)
 integer(4) :: loadifs, n, k
 ! Задаем имена СИФ
 character(12) :: fn(17) = (/ 'Curl', 'Tree', 'Davis', 'Leaf', 'Binary', 'Coral', &
  'Crystal', 'Dragon', 'Fern', 'Floor', 'Koch', 'Spiral', &
  'Swirl', 'Triang', 'Triangle', 'Zigzag', 'Koch2' /)
 call initGraph()
 do k = 1, 17 ! Обработка 17 СИФ; их имена содержит вектор fn
  n = loadifs(ifs, fn(k), nc) ! Читаем очередной СИФ из файла frctls.txt
  if(n == 0) then ! Если СИФ не найден
   ! Используем С-строки
   rslt = MESSAGEBOXQQ("Cannot load fractal " // fn(k) // ""C, "IFS"C, MB$OK)
   stop
  end if
  call fconv(ifs, n) ! Поиск minx, miny, maxx, maxy
  call render(ifs, n) ! Вывод nm точек изображения очередного СИФ
  call sleepqq(300) ! Задержка на 300 миллисекунд
 end do
end program fract
!
function loadifs(ifs, name, nc)
 integer(4):: loadifs
 real(8) :: ifs(nc)
 character(*) :: name
 character(len(name)) :: st
 open(1, file = 'frctls.txt')
 do while(.not. eof(1))
  read(1, *) st
  if(st == name) exit
 end do
 if(eof(1)) then
  loadifs = 0
  return
 end if
 read(1, *) ifs
 close(1)
 loadifs = 4
end function loadifs

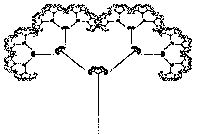
Результаты работы программы приведены в табл. 2.

Табл. 2. Некоторые фракталы, порождаемые СИФ из файла frctls.txt

Curl	Tree	Davis
Leaf	Binary	Coral
Crystal	Dragon	Fern
Floor	Spiral	Swirl

Морфинг СИФ

Морфинг СИФ - это постепенное преобразование одного изображения в другое, осуществляемое в результате смешения СИФ двух изображений. При этом доля исходного СИФ в смеси СИФ по мере преобразования уменьшается, а доля СИФ-результата увеличивается.
Смешение СИФ, хранящихся в массивах ifs1 и ifs2, можно осуществить, скажем, так:

! Линейная интерполяция двух СИФ
ifs = (1.0 - phase) * ifs1 + phase * ifs2 ! ifs - массив результирующего СИФ

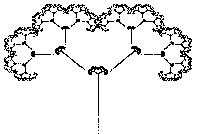
Морфинг-преобразование Tree в Leaf выполнит программа morph. Результат работы программы приведен в табл. 3.

Табл. 3. Морфинг Tree в Leaf

1.0 * Tree + 0.0 * Leaf	0.9 * Tree + 0.1 * Leaf	0.8 * Tree + 0.2 * Leaf
0.6 * Tree + 0.4 * Leaf	0.5 * Tree + 0.5 * Leaf	0.4 * Tree + 0.6 * Leaf
0.2 * Tree + 0.8 * Leaf	0.1 * Tree + 0.9 * Leaf	0.0 * Tree + 1.0 * Leaf

program morph
 use ifqwin
 use screen2
 implicit none
 real(8) :: ifs(nc) , Tree(nc), Leaf(nc)
 real(8) :: phase, df = 0.1_8
 integer(4) :: loadifs
 integer(4) :: n, n1
 n = loadifs(Tree, 'Tree', nc) ! Загрузка СИФ для Tree
 n1 = loadifs(Leaf, 'Leaf', nc) ! Загрузка СИФ для Leaf
 if(n == 0 .or. n1 == 0) then
  rslt = MESSAGEBOXQQ("Cannot load fractal Tree or Leaf"C, "IFS"C, MB$OK)
  stop
 end if
 call initGraph() ! Инициализация графического режима
 phase = 0.0_8
 do while(phase < 1.0)
  ! Линейная интерполяция двух СИФ
  ifs = (1.0 - phase) * Tree + phase * Leaf ! ifs - массив результирующего СИФ
  call fconv(ifs, n) ! Поиск minx, miny, maxx, maxy
  call render(ifs, n) ! Вывод изображения
  call sleepqq(300) ! Задержка на 300 миллисекунд
  phase = phase + df ! Изменяем пропорции смешения СИФ
 end do
end program morph
!
function loadifs(ifs, name, nc)
 integer(4):: loadifs
 real(8) :: ifs(nc)
 character(*) :: name
 character(len(name)) :: st
 open(1, file = 'frctls.txt')
 do while(.not. eof(1))
  read(1, *) st
  if(st == name) exit
 end do
 if(eof(1)) then
  loadifs = 0
  return
 end if
 read(1, *) ifs
 close(1)
 loadifs = 4
end function loadifs

Алгебраические фракталы

Алгебраические фракталы получают с помощью нелинейных процессов в n-мерных пространствах.
Нелинейные динамические системы обладают в общем случае несколькими устойчивыми состояниями. То состояние, в котором оказалась динамическая система после некоторого числа итераций, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом, фазовое пространство системы разбивается на области притяжения аттракторов. Если фазовым является двумерное пространство, то, окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы (итерационного процесса). Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами.

Множество Мандельброта

Возьмем функцию комплексного переменного f(z) = z² + c. Положим z₀ = 0 и рассмотрим последовательность {z_n}, где ∀i > 0: z_i = f(z_i). Такая последовательность может быть ограниченной (то есть может существовать такое R, что ∀i: | z_i | < R), либо убегать в бесконечность (то есть ∀ R > 0 ∃ i: | z_i | > R).

Множество Мандельброта можно определить как множество комплексных чисел c, для которых указанная последовательность является ограниченной. Неизвестно аналитического выражения, которое позволяло бы по данному с определить, принадлежит ли оно множеству Мандельброта или нет. Поэтому для построения множества используют компьютерный эксперимент: просматривают с некоторым шагом множество точек на комплексной плоскости; для каждой точки проводят определенное число итераций (находят определенное число членов последовательности) и смотрят за ее поведением.
Доказано, что множество Мандельброта размещается в круге радиуса 2 с центром в начале координат. Таким образом, если на некотором шаге модуль очередного члена последовательности превышает 2, то можно сделать вывод, что точка, соответствующая с, определяющему данную последовательность, не принадлежит множеству Мандельброта. Впрочем, если проделать большое, но конечное число итераций, а точки так и останутся в круге радиуса 2, то нельзя гарантировать, что с принадлежит множеству Мандельброта. Уменьшая шаг, с которым просматриваются комплексные числа, и увеличивая количество итераций, можно получать сколь угодно подробные, но всегда лишь приближенные изображения множества.
Для генерации множества можно употребить следующую программу:

module screen2
 integer(2) rslt, YE ! Y - размер экрана (в пикселях)
 integer(4), parameter :: nm = 150000 ! Число исследуемых точек
 integer(4), parameter :: nc = 500 ! Число проверочных итераций
end module screen2
!
subroutine initGraph() ! Инициализация графического режима
 use ifqwin
 use screen2
 type(windowconfig) wc
 rslt = setbkcolorrgb(#ffffff) ! Белый цвет фона
 call clearscreen($gclearscreen) ! Заливка экрана цветом фона
 rslt = getwindowconfig(wc)
 YE = wc.numypixels ! Число пикселей по оси Y
 ! Задаем видовой порт размером в центре окна вывода
 call setviewport(10, 10, YE / 3_2, YE / 3_2)
 ! Работаем в оконной системе координат с двойной точностью
 rslt = setcolor(0) ! Текущий свет - черный
end subroutine initGraph
!
program mandelbrot ! Вывод множества Мандельброта
 use ifqwin
 use screen2
 implicit none
 real(4) :: r1, r2, r3 ! Псевдослучайные числа
 real(8) :: k2
 logical(4) :: flag
 complex(8) :: c, z
 integer(4) :: i, j
 logical(2) :: finv = .true.
 call initGraph() ! Инициализация графического режима
 ! Задаем оконную систему координат, указывая диапазон изменения x и y
 rslt = setwindow(finv, -2, -2, 2, 2)
 ! Множитель для перевода случайных чисел в комплексное число с
 k2 = sqrt(2.0)
 do i = 1, nm ! Исследуем nm точек комплексной плоскости
  call random(r1) ! на предмет их принадлежности множеству
  call random(r2) ! Мандельброта
  call random(r3) ! Случайным образом устанавливаем знаки чисел r1 и r2
  if(r3 < 0.5) r1 = -r1
  call random(r3)
  if(r3 < 0.5) r2 = -r2
  c = cmplx(k2 * r1, k2 * r2) ! Формируем комплексное число с
  z = (0.0, 0.0) ! Начальное значение проверочной переменной
  flag = .true.
  ! Используем для установления факта принадлежности комплексного числа с множеству Мандельброта nc итераций
  do j = 1, nc
   z = z * z + c
   if(abs(z) > 2.0) then
    flag = .false.
    exit
   end if
  end do
  ! Считаем, что число с принадлежит множеству Мандельброта
  if(flag) then
   rslt = setpixel_w(real(c), aimag(c)) ! Выводим очередную точку изображения
  end if
 end do
 ! Выводим окружность радиуса 2; ее центр разместим в центре окна вывода
 rslt = ellipse_w($gborder, -2, -2, 2, 2)
end program mandelbrot

Результат работы программы mandelbrot приведен на рис. 9.

Рис. 9. Приближенное изображение множества Мандельброта, обведенное окружностью радиуса 2

Множество Жюлиа

Множество Жюлиа тесно связано с множеством Мандельброта. Множество Жюлиа J(f) определяется как

J(f) = δ, {z: |f ⁿ(z)| → ∞ при n → ∞}.

Иными словами, множество Жюлиа функции f есть граница множества точек z, для которых справедливо:

|f ⁿ (z)| → ∞ при n → ∞.

Простейшее множество Жюлиа соответствует случаю f (z) = z².

Так как в этом случае f ⁿ(z) = z²ⁿ, то |f ⁿ(z)| → ∞ при n → ∞ тогда и только тогда, когда | z | > 1. Границей этого множества точек z является множество Жюлиа в виде единичной окружности {z : | z | = 1}.

Рассмотрим способ построения множеств Жюлиа для функции комплексного переменного f(z) = z² + с, например при с = -1.0. Возьмем прямоугольник (x₁, у₁), (x₂, y₂).
Зафиксируем константу с и будем случайным образом выбирать точки в пределах взятого прямоугольника. Для каждой точки проверим, как меняется |f ⁿ(z)| при n → ∞.
Вывод множества Жюлиа функции f(z) = z² + с обеспечит следующая программа:

module screen2
 integer(2) rslt, XE, YE ! XE, YE - размеры экрана (в пикселях)
 integer(4), parameter :: nm = 150000 ! Число исследуемых точек
 integer(4), parameter :: nc = 500 ! Число проверочных итераций
end module screen2
!
subroutine initGraph() ! Инициализация графического режима
 use ifqwin
 use screen2
 type(windowconfig) wc
 rslt = setbkcolorrgb(#ffffff) ! Белый цвет фона
 call clearscreen($gclearscreen) ! Заливка экрана цветом фона
 rslt = getwindowconfig(wc)
 XE = wc.numxpixels; YE = wc.numypixels ! Число пикселей по осям X и Y
 ! Задаем видовой порт размером в центре окна вывода
 call setviewport(10, 10, YE / 3_2, YE / 3_2)
 ! Работаем в оконной системе координат с двойной точностью
 rslt = setcolor(0) ! Текущий свет - черный
end subroutine initGraph
!
program julia ! Вывод множества Жюлиа
 use ifqwin
 use screen2
 real(4) r1, r2, r3 ! Псевдослучайные числа
 logical(2) :: finv = .true., flag
 complex(8) :: c = -1.0, z, f, z2
 real(8) :: x = 2.0_8, y = 2.0_8 ! Для задания исследуемого прямоугольника
 integer(4) i
 call initGraph() ! Инициализация графического режима
 ! Задаем оконную систему координат, указывая диапазон изменения x и y
 rslt = setwindow(finv, -x, -y, x, y)
 do i = 1, nm ! Исследуем nm точек комплексной плоскости на предмет их принадлежности множеству Жюлиа
  call random(r1)
  call random(r2)
  call random(r3) ! Случайным образом устанавливаем знаки
  if(r3 < 0.5) r1 = -r1 ! чисел r1 и r2
  call random(r3)
  if(r3 < 0.5) r2 = -r2
  z = cmplx(x * r1, y * r2) ! Формируем комплексное число z
  z2 = z
  flag = .true.
  ! Используем для установления факта принадлежности комплексного числа z множеству Жюлиа nc итераций
  do j = 1, nc
   z2 = z2 * z2 + c
   if(abs(z2) > 4.0) then
    flag = .false.
    exit
   end if
  end do
  ! Если значение flag истинно, то число z находится в пределах искомого множества Жюлиа
  if(flag) rslt = setpixel_w(real(z), aimag(z)) ! Выводим очередную точку изображения
 end do
 ! Выводим окружность радиуса 2; ее центр разместим в центре окна вывода
 rslt = ellipse_w($gborder, -2, -2, 2, 2)
end program julia

Результат работы программы приведен на рис. 10.

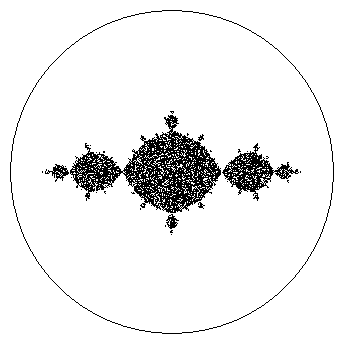
Рис. 10. Приближенное изображение точек, лежащих в пределах множества Жюлиа, обведенное окружностью радиуса 2

Стохастические фракталы

Еще одним известным классом фракталов являются стохастические (случайные) фракталы, которые получаются, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом можно получить объекты напоминающие природные - несимметричные деревья, изрезанные береговые линии и т. д. Поэтому стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
Используя случайные возмущения, можно, например, построить снежинку Коха, добавляя на каждом шаге треугольники, обращенные как во внутрь, так и в наружу (рис. 11). Причем выбор ориентации треугольника осуществляется случайным образом.

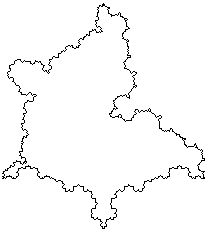
Рис. 11. Рандомизированная снежинка Коха

Основной моделью, применяемой при генерации стохастических фракталов, является фрактальное броуновское движение - случайный процесс, широко распространенный в природе и исследованный Мандельбротом и Ван Нессом. В отличие от классического броуновского движения, фрактальное броуновское движение обладает некоторой памятью, зависимыми приращениями, не является марковским процессом и определяется при помощи параметра H, 0 < H < 1 (параметр Херста). При H = 1/2 фрактальное броуновское движение совпадает с классическим.

Литература

1. Гарднер М. От мозаик Пенроуза к надежным шифрам. - М.: Мир, 1993.
2. Кроновер Р. М. Фракталы и хаос в динамических системах. Основы теории. - М.: Постмаркет, 2000.
3. Леви П. Стохастические процессы и броуновское движение. - М.: Наука, 1972.
4. Пайтген Х., Рихтер П. Красота фракталов. Образы комплексных динамических систем. - М.: Мир, 1993.
5. Barnsley M. Fractals Everywhere. Academic Press, Boston, 1988.
6. Hausdorff F. Dimension und Ausseres Mass. Mathematische Annalen, V 79, 1919, pp. 157-179.
7. Hutchinson J. Fractals and Self Similarity. Indiana University Mathematics Journal, V 30, N 5, 1981, pp. 713-747.
8. Mandelbrot B. The Fractal Geometry of Nature. Freeman, San Francisco, 1982.

Список работ