

Приводятся некоторые средства библиотеки pyglet для работы с OpenGL. Программирование выполняется на Python 3.6.6. Рассматривается вывод примитивов, заливка полигона с использованием растрового образа, применение материалов, наложение текстуры и употребление шейдеров.
Предполагается, что читатель знаком с основами компьютерной графики и OpenGL. По этой причине опускается рассмотрение вопросов проецирования, аффинных преобразований координат, систем цветов и пр., так же как и процедур и функций OpenGL.
Некоторые сведения об OpenGL можно найти, например, в [1-9].
Программирование вывода прямоугольника позволит привести код, обеспечивающий визуализацию на основе pyglet OpenGL.
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window
dx, dy = 25, 15 # Размеры прямоугольника
dx2 = dx / 2
dy2 = dy / 2
wx, wy = 1.5 * dx2, 1.5 * dy2 # Параметры области визуализации
width, height = int(20 * wx), int(20 * wy) # Размеры окна вывода
# Создаем окно визуализации
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Прямоугольник')
gl.glClearColor(0.1, 0.1, 0.1, 1.0) # Задаем почти черный цвет фона
gl.glClear(gl.GL_COLOR_BUFFER_BIT) # Заливка окна цветом фона
@window.event
def on_draw():
# Проецирование
gl.glMatrixMode(gl.GL_PROJECTION) # Теперь текущей является матрица проецирования
gl.glLoadIdentity() # Инициализация матрицы проецирования
gl.glOrtho(-wx, wx, -wy, wy, -1, 1) # Ортографическое проецирование
gl.glColor3f(0, 1, 0) # Зеленый цвет
gl.glBegin(gl.GL_QUADS) # Обход против часовой стрелки
gl.glVertex3f(-dx2, -dy2, 0)
gl.glVertex3f(dx2, -dy2, 0)
gl.glVertex3f(dx2, dy2, 0)
gl.glVertex3f(-dx2, dy2, 0)
gl.glEnd()
app.run()
Результат показан на рис. 1.
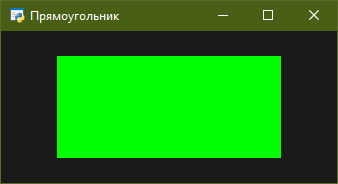
Рис. 1. Прямоугольник
Тот же результат получим, применив graphics.draw [10] (приводится только процедура on_draw).
@window.event
def on_draw():
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-wx, wx, -wy, wy, -1, 1)
graphics.draw(4, gl.GL_QUADS,
('v2f', (-dx2, -dy2, dx2, -dy2, dx2, dy2, -dx2, dy2)),
('c3f', (0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0)))
Первый параметр – это число вершин, далее следуют кортежи с координатами вершин и их цветом.
Цвет можно задать перед graphics.draw:
gl.glColor3f(0, 1, 0)
graphics.draw(4, gl.GL_QUADS,
('v2f', (-dx2, -dy2, dx2, -dy2, dx2, dy2, -dx2, dy2)))
Так же можно употребить graphics.vertex_list:
@window.event
def on_draw():
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-wx, wx, -wy, wy, -1, 1)
v_lst = graphics.vertex_list(4,
('v2f', (-dx2, -dy2, dx2, -dy2, dx2, dy2, -dx2, dy2)),
('c3f', (0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0)))
v_lst.draw(gl.GL_QUADS)
При выводе нескольких примитивов, например треугольников, с общими вершинами более компактным будет применение graphics.draw_indexed, например:
@window.event
def on_draw():
# Проецирование
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-wx, wx, -wy, wy, -1, 1)
graphics.draw_indexed(4, gl.GL_TRIANGLES,
[0, 1, 2, 1, 3, 2],
('v2f', (-dx2, -dy2, 0, -dy / 4, 0, dy2, dx2, -dy2)),
('c3f', (1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0)))
Всего для вывода двух смежных треугольников (рис. 2 ) достаточно задать 4 вершины.
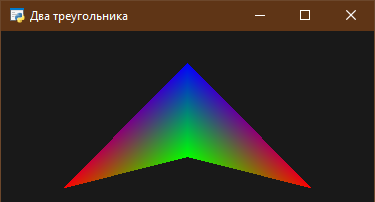
Рис. 2. Треугольники
Чтобы отключить интерполяцию цветов, перед graphics.draw_indexed следует задать
gl.glShadeModel(gl.GL_FLAT) # По умолчанию употребляется GL_SMOOTH
Будет использован цвет вершины с индексом 2 – (0, 1, 0).
Для точки можно задать ее размер:
gl.glPointSize(16)
и режим сглаживания:
gl.glEnable(gl.GL_POINT_SMOOTH)
Отобразим 8 точек: 4, используя glBegin / glEnd, и 4 сглаженные, применив draw, (рис. 3):
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window
d, d2 = 12, 10
wx, wy = 1.5 * d, 1.2 * d # Параметры области визуализации
width, height = int(20 * wx), int(20 * wy) # Размеры окна вывода
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Точки')
gl.glClearColor(0.1, 0.1, 0.1, 1.0)
gl.glClear(gl.GL_COLOR_BUFFER_BIT)
@window.event
def on_draw():
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-wx, wx, -wy, wy, -1, 1)
gl.glPointSize(16)
gl.glBegin(gl.GL_POINTS)
gl.glColor3f(1, 0, 0)
gl.glVertex3f(-d, -d, 0)
gl.glColor3f(0, 1, 0)
gl.glVertex3f(-d, d, 0)
gl.glColor3f(0, 0, 1)
gl.glVertex3f(d, d, 0)
gl.glColor3f(1, 1, 0)
gl.glVertex3f(d, -d, 0)
gl.glEnd()
gl.glEnable(gl.GL_POINT_SMOOTH)
graphics.draw(4, gl.GL_POINTS,
('v2f', (-d2, -d2, -d2, d2, d2, d2, d2, -d2)),
('c3B', (0, 0, 255, 0, 255, 0, 255, 0, 0, 255, 255, 0)))
gl.glDisable(gl.GL_POINT_SMOOTH)
app.run()

Рис. 3. Точки
Для линии можно задать ее толщину:
gl.glLineWidth(4)
и образец (маску):
gl.glEnable(gl.GL_LINE_STIPPLE)
pattern = '0b1111100110011111' # '1111100110011111'
gl.glLineStipple(2, int(pattern, 2)) # Повторяем каждый бит образца 2 раза
Линии (рис. 4) выводятся после задания GL_LINES, или GL_LINE_STRIP, или GL_LINE_LOOP:
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window
d, d2, d3 = 12, 8, 6
wx, wy = 1.5 * d, 1.2 * d # Параметры области визуализации
width, height = int(20 * wx), int(20 * wy) # Размеры окна вывода
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Линии')
gl.glClearColor(0.1, 0.1, 0.1, 1.0)
gl.glClear(gl.GL_COLOR_BUFFER_BIT)
@window.event
def on_draw():
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-wx, wx, -wy, wy, -1, 1)
gl.glLineWidth(4)
gl.glBegin(gl.GL_LINES)
gl.glColor3f(1, 0, 0)
gl.glVertex3f(-d, -d, 0)
gl.glVertex3f(-d, d, 0)
gl.glColor3f(0, 1, 0)
gl.glVertex3f(-d, d, 0)
gl.glVertex3f(d, d, 0)
gl.glColor3f(0, 0, 1)
gl.glVertex3f(d, d, 0)
gl.glVertex3f(d, -d, 0)
gl.glColor3f(1, 1, 0)
gl.glVertex3f(d, -d, 0)
gl.glVertex3f(-d, -d, 0)
gl.glEnd()
graphics.draw(5, gl.GL_LINE_STRIP,
('v2f', (-d, -d, -d, d, d, d, d, -d, -d, -d)),
('c3f', (1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0)))
gl.glEnable(gl.GL_LINE_STIPPLE)
pattern = '0b1111100110011111' # '1111100110011111'
gl.glLineStipple(2, int(pattern, 2)) # Повторяем каждый бит образца 2 раза
gl.glColor3f(1, 1, 1)
gl.glBegin(gl.GL_LINE_STRIP)
gl.glVertex3f(-d2, -d2, 0)
gl.glVertex3f(-d2, d2, 0)
gl.glVertex3f(d2, d2, 0)
gl.glVertex3f(d2, -d2, 0)
gl.glVertex3f(-d2, -d2, 0)
gl.glEnd()
graphics.draw(4, gl.GL_LINE_LOOP,
('v2f', (-d3, -d3, -d3, d3, d3, d3, d3, -d3)))
gl.glDisable(gl.GL_LINE_STIPPLE)
app.run()

Рис. 4. Линии
Лицевая сторона будет показана, если при выводе многоугольника его вершины обходятся против часовой стрелки, в противном случае будет наблюдаться нелицевая сторона многоугольника. Каждая из сторон может быть показана либо в виде точек в вершинах многоугольника, либо в виде линий, либо залита одним цветом, либо залита с использованием интерполяции цветов, указанных в вершинах многоугольника, либо залита с использованием образца, текстуры или материала. Эти возможности, кроме трех последних, демонстрирует нижеприводимая программа, в которой первоначально левый прямоугольник выводится лицевой стороной, а правый – нелицевой, причем с интерполяцией цветов (рис. 5), поскольку вершины имеют разные цвета, а по умолчанию имеем glShadeModel(GL_SMOOTH).
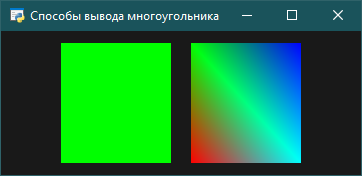
Рис. 5. По умолчанию для GL_FRONT_AND_BACK установлено GL_FILL
Затем после нажатия на клавишу 1 лицевая сторона выводится в виде точек, а нелицевая – в виде линий (рис. 6).
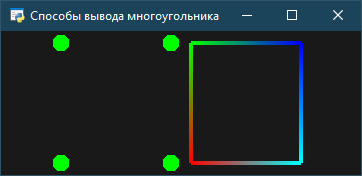
Рис. 6. После нажатия на 1
После нажатия на клавишу 2 картина меняется: лицевая сторона выводится в виде линий, а нелицевая – в виде точек (рис. 7).
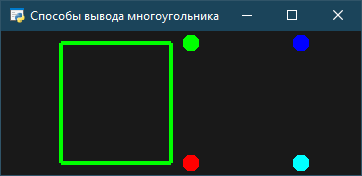
Рис. 7. После нажатия на 2
После нажатия на 3 оба прямоугольника заливаются без интерполяции цветов (рис. 8), а после нажатия на 4 получаем рис. 5.
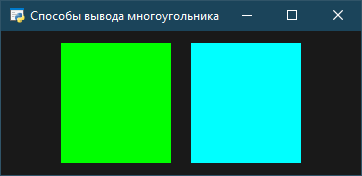
Рис. 8. После нажатия на 3
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window, key
d = 12
d2 = 6
wx, wy = 1.5 * d, 1.2 * d2 # Параметры области визуализации
width, height = int(20 * wx), int(20 * wy) # Размеры окна вывода
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Способы вывода многоугольника')
gl.glClearColor(0.1, 0.1, 0.1, 1.0)
gl.glClear(gl.GL_COLOR_BUFFER_BIT)
gl.glEnable(gl.GL_POINT_SMOOTH)
gl.glPointSize(16)
gl.glLineWidth(4)
@window.event
def on_draw():
window.clear()
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-wx, wx, -wy, wy, -1, 1)
gl.glBegin(gl.GL_QUADS)
gl.glColor3f(0, 1, 0)
gl.glVertex3f(-d, -d2, 0)
gl.glVertex3f(-1, -d2, 0)
gl.glVertex3f(-1, d2, 0)
gl.glVertex3f(-d, d2, 0)
gl.glEnd()
graphics.draw(4, gl.GL_QUADS,
('v2f', (1, -d2, 1, d2, d, d2, d, -d2)),
('c3f', (1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1)))
@window.event
def on_key_press(symbol, modifiers):
mode_f = mode_b = None
c = chr(symbol)
if c == '1': # c == key._1
mode_f = gl.GL_POINT
mode_b = gl.GL_LINE
shade_model = gl.GL_SMOOTH
elif symbol == key._2:
mode_f = gl.GL_LINE
mode_b = gl.GL_POINT
shade_model = gl.GL_SMOOTH
elif symbol == key._3:
mode_f = mode_b = gl.GL_FILL
shade_model = gl.GL_FLAT
elif symbol == key._4:
mode_f = mode_b = gl.GL_FILL
shade_model = gl.GL_SMOOTH
if mode_f is not None:
gl.glPolygonMode(gl.GL_FRONT, mode_f)
gl.glPolygonMode(gl.GL_BACK, mode_b)
gl.glShadeModel(shade_model)
app.run()
Образец размера 32*32 бита приведен на рис. 9.

Рис. 9. Образец
Он задается массивом mask из 128 элементов. Тип массива __main__.c_ubyte_Array_128. Каждые 4 элемента массива содержат 32 бита и определяют одну строку образца. Образец используется после задания
gl.glEnable(gl.GL_POLYGON_STIPPLE)
gl.glPolygonStipple(mask)
Результат показан на рис. 10.

Рис. 10. Заливка по образцу
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window, key
d = 12
d2 = 6
wx, wy = 1.5 * d, 1.2 * d2 # Параметры области визуализации
width, height = int(20 * wx), int(20 * wy) # Размеры окна вывода
# Муха
mask0 = [0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x00, 0x03, 0x80, 0x01, 0xc0, 0x06, 0xc0, 0x03, 0x60,
0x04, 0x60, 0x06, 0x20, 0x04, 0x30, 0x0c, 0x20, 0x04, 0x18, 0x18, 0x20, 0x04, 0x0c, 0x30, 0x20,
0x04, 0x06, 0x60, 0x20, 0x44, 0x03, 0xc0, 0x22, 0x44, 0x01, 0x80, 0x22, 0x44, 0x01, 0x80, 0x22,
0x44, 0x01, 0x80, 0x22, 0x44, 0x01, 0x80, 0x22, 0x44, 0x01, 0x80, 0x22, 0x44, 0x01, 0x80, 0x22,
0x66, 0x01, 0x80, 0x66, 0x33, 0x01, 0x80, 0xcc, 0x19, 0x81, 0x81, 0x98, 0x0c, 0xc1, 0x83, 0x30,
0x07, 0xe1, 0x87, 0xe0, 0x03, 0x3f, 0xfc, 0xc0, 0x03, 0x31, 0x8c, 0xc0, 0x03, 0x33, 0xcc, 0xc0,
0x06, 0x64, 0x26, 0x60, 0x0c, 0xcc, 0x33, 0x30, 0x18, 0xcc, 0x33, 0x18, 0x10, 0xc4, 0x23, 0x08,
0x10, 0x63, 0xc6, 0x08, 0x10, 0x30, 0x0c, 0x08, 0x10, 0x18, 0x18, 0x08, 0x10, 0x00, 0x00, 0x08]
dim = 128
mask = (gl.GLubyte * dim)()
for k in range(dim):
mask[k] = mask0[k]
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Заливка по образцу')
gl.glClearColor(0.1, 0.1, 0.1, 1.0)
gl.glClear(gl.GL_COLOR_BUFFER_BIT)
@window.event
def on_draw():
window.clear()
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-wx, wx, -wy, wy, -1, 1)
gl.glEnable(gl.GL_POLYGON_STIPPLE)
gl.glPolygonStipple(mask)
gl.glBegin(gl.GL_QUADS)
gl.glColor3f(0, 1, 0)
gl.glVertex3f(-d, -d2, 0)
gl.glVertex3f(-1, -d2, 0)
gl.glVertex3f(-1, d2, 0)
gl.glVertex3f(-d, d2, 0)
gl.glEnd()
graphics.draw(4, gl.GL_QUADS,
('v2f', (1, -d2, 1, d2, d, d2, d, -d2)),
('c3f', (1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1)))
app.run()
Вывод текстуры регулируется ее координатами (glTexCoord2f) и параметрами (glTexParameterf). Цвет полигона определяется либо чисто текстурой, либо в результате смешения цвета полигона и текстуры (glTexEnvf).
Текстура обычно создается на основе растрового образа, загружаемого из файла (рис. 11), но может быть создана и программно (рис. 12).

Рис. 11. Текстура на основе файла; tile_x = 2, tile_y = 1
tile_x, tile_y – соответственно число повторов текстуры по X и Y.

Рис. 12. Программно сгенерированная текстура; tile_x = tile_y = 1
Оба результата получены следующим кодом:
from pyglet.gl import *
from pyglet import app
from pyglet.window import Window, key
d = 12
wx, wy = 1.5 * d, 1.1 * d # Параметры области визуализации
width, height = int(20 * wx), int(20 * wy) # Размеры окна вывода
texFromFile = True # True False
if texFromFile:
tile_x = 2 # Число повторов текстуры по X
tile_y = 1 # Число повторов текстуры по Y
else:
tile_x = tile_y = 1
def to_c_float_Array(data): # Преобразование в си-массив
return (GLfloat * len(data))(*data)
vld = to_c_float_Array([-d, -d, 0]) # Левая нижняя вершина
vrd = to_c_float_Array([d, -d, 0]) # Правая нижняя вершина
vru = to_c_float_Array([d, d, 0]) # Правая верхняя вершина
vlu = to_c_float_Array([-d, d, 0]) # Левая верхняя вершина
#
def texInit():
if texFromFile:
fn = 'G:\\python\\openGL\\кот.jpg'
img = pyglet.image.load(fn)
iWidth = img.width
iHeight = img.height
img = img.get_data('RGB', iWidth * 3)
else:
iWidth = iHeight = 64 # Размер текстуры равен iWidth * iHeight
n = 3 * iWidth * iHeight
# Каждый элемент текстуры содержит три компонента (формат текстуры GL_RGB)
# GL_UNSIGNED_BYTE - это диапазон 0-255, поэтому для img задается тип uint8, а затем GLubyte
img = np.zeros((3, iWidth, iHeight), dtype = 'uint8')
for i in range(iHeight): # Генерация черно-белого образа, на основе которого создается текстура
for j in range(iWidth):
img[:, i, j] = ((i - 1) & 16 ^ (j - 1) & 16) * 255
img = img.reshape(n)
img = (GLubyte * n)(*img)
p = GL_TEXTURE_2D
r = GL_RGB
# Задаем параметры текстуры
glTexParameterf(p, GL_TEXTURE_WRAP_S, GL_REPEAT) # GL_CLAMP
glTexParameterf(p, GL_TEXTURE_WRAP_T, GL_REPEAT)
glTexParameterf(p, GL_TEXTURE_MAG_FILTER, GL_LINEAR)
glTexParameterf(p, GL_TEXTURE_MIN_FILTER, GL_LINEAR)
# Способ взаимодействия с текущим фрагментом изображения
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_DECAL)
# Создаем 2d-текстуру на основе образа img
glTexImage2D(p, 0, r, iWidth, iHeight, 0, r, GL_UNSIGNED_BYTE, img)
glEnable(p)
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Текстура')
glClearColor(0.1, 0.1, 0.1, 1.0)
glClear(GL_COLOR_BUFFER_BIT)
texInit()
@window.event
def on_draw():
window.clear()
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
glOrtho(-wx, wx, -wy, wy, -1, 1)
glBegin(GL_QUADS)
glTexCoord2f(0, 0);
glVertex3fv(vld)
glTexCoord2f(tile_x, 0)
glVertex3fv(vrd)
glTexCoord2f(tile_x, tile_y)
glVertex3fv(vru)
glTexCoord2f(0, tile_y)
glVertex3fv(vlu)
glEnd()
app.run()
Материалы позволяют получать, с одной стороны, изображения, похожие на реальные, так и реализовывать различные цветовые фантазии. Материал применяется в режиме расчета освещенности:
gl.glEnable(gl.GL_LIGHTING)
Помимо этого задаются цвет материала, цвет источника света, его позиция и нормали к вершинам полигонов. На рис. 13 показан прямоугольник, в трех вершинах которого нормали обращены к источнику света, в четвертой вершине угол между нормалью и направлением света близок к 180°. По этой причине цвет этой вершины почти черный.

Рис. 13. Выполнен расчет освещенности
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window, key
import numpy as np
from sys import exit
d = 12
wx, wy = 1.5 * d, 1.1 * d # Параметры области визуализации
width, height = int(20 * wx), int(20 * wy) # Размеры окна вывода
#
mtClr0 = [1, 1, 0, 0] # Цвет материала
light_position0 = [0, 40, 40, 0] # Позиция источника света
lghtClr0 = [0.75, 0, 0, 0] # Цвет источника света
mtClr = (gl.GLfloat * 4)()
light_position = (gl.GLfloat * 4)()
lghtClr = (gl.GLfloat * 4)()
for k in range(4): mtClr[k] = mtClr0[k]
for k in range(4): light_position[k] = light_position0[k]
for k in range(4): lghtClr[k] = lghtClr0[k]
#
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Материал')
gl.glClearColor(0.1, 0.1, 0.1, 1.0)
gl.glClear(gl.GL_COLOR_BUFFER_BIT)
gl.glEnable(gl.GL_LIGHTING) # Активизируем использование материалов
@window.event
def on_draw():
window.clear()
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-wx, wx, -wy, wy, -1, 1)
gl.glShadeModel(gl.GL_SMOOTH) # GL_FLAT - без интерполяции цветов
gl.glMaterialfv(gl.GL_FRONT, gl.GL_SPECULAR, mtClr)
gl.glLightfv(gl.GL_LIGHT0, gl.GL_POSITION, light_position)
gl.glLightfv(gl.GL_LIGHT0, gl.GL_SPECULAR, lghtClr)
gl.glEnable(gl.GL_LIGHT0) # Включаем в уравнение освещенности источник GL_LIGHT0
gl.glColor3f(1, 0, 0)
gl.glBegin(gl.GL_QUADS)
gl.glNormal3f(0, 0, 1)
gl.glVertex3f(-d, -d, 0)
gl.glNormal3f(0, 0, 1)
gl.glVertex3f(d, -d, 0)
gl.glNormal3f(0, 0, 1)
gl.glVertex3f(d, d, 0)
gl.glNormal3f(0, 0, -1)
gl.glVertex3f(-d, d, 0)
gl.glEnd()
@window.event
def on_key_press(symbol, modifiers):
if symbol == key._1:
gl.glDisable(gl.GL_LIGHTING)
elif symbol == key._2:
gl.glEnable(gl.GL_LIGHTING)
app.run()
Цвет полигона будет определяться glColor3f, если отказаться от использования материала:
gl.glDisable(gl.GL_LIGHTING)
Это произойдет при нажатии на 1. После нажатия на 2 материал будет применен вновь.
Выводится параболоид (рис. 14)
y = a*x2 + a*z2
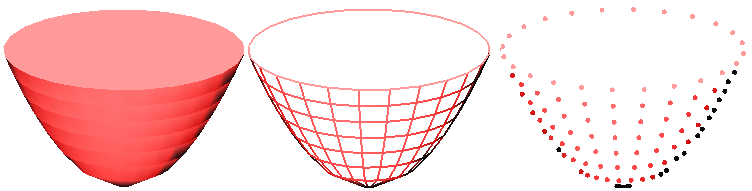
Рис. 14. Параболоид
Нормали рассчитываются к граням в каждой вершине параболоида (гранью является трапеция).
Разницу между нормалью к грани и к вершине иллюстрирует рис. 14.
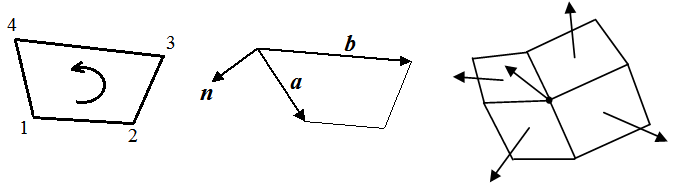
Рис. 15. Порядок вывода вершин, нормаль к грани и нормаль к вершине
Вычисление нормали:
import numpy as np
n = np.cross(a, b) # Векторное произведение
n = n / np.linalg.norm(n) # Нормализация
или
n = n / np.sqrt(np.sum(n**2)) # Нормализация
Замечание.OpenGL выполнит нормализацию самостоятельно, если задать:
glEnable(GL_NORMALIZE)
Нормали к грани задаются во всех вершинах (нормали к вершине не вычисляются, поэтому видны слои фигуры даже при использовании GL_SMOOTH).
Параболоид с нормалями показан на рис. 16.
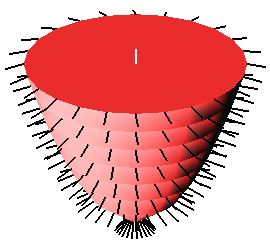
Рис. 16. Параболоид с нормалями
После отказа от сглаживания видны отдельные грани:

Рис. 17. Параболоид: gl.glShadeModel(gl.GL_FLAT)
При выводе текстуры (сгенерированной или из файла) имеем рис. 18.

Рис. 18. Параболоид с текстурой
# Вывод параболоида
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window, key
import numpy as np, math
from sys import exit
# z = ac*x**2 + ac*y**2 (реально имеем: y = ac*x**2 + ac*z**2)
save_to_file = True # Флаг записи модели в файлы
read_from_file = True # Флаг чтения модели из файлов
if read_from_file: save_to_file = False
plot_surf = False # Флаг вывода поверхности z = ac*x**2 + ac*y**2
show_top = True # Флаг вывода крышки
show_normals = True
kn = 2 # Коэффициент увеличения длины отображаемой нормали
ac = 2.5 # Коэффициент в уравнении параболоида
n = 24 # Число вершин в сечении параболоида
ch = 7 # Число сечений параболоида плоскостями y = const
h_cover = 20 # Высота параболоида
vrts = [] # Координаты вершин параболоида
nrms = [] # Координаты нормалей к граням (рассчитываются для каждой вершины)
textr = [] # Координаты текстуры (задаются для каждой вершины)
vrts_top = [] # Координаты вершин крышки
textr_top = [] # Координаты тектстуры крышки
dh = h_cover / ch # Расстояние между сечениями
dal = 2 * math.pi / n # dal - угол между вершинами сечения
hp0 = 0.1 # Низ параболоида
# Текстура
use_txtr = True
texFromFile = True # True False
if use_txtr: show_normals = False
# Координаты текстуры меняются в диапазоне 0-1
dnx = 1 / (n - 1) # Шаг изменения координат текстуры по x
dny = 1 / ch # Шаг изменения координат текстуры по y
if read_from_file:
print('Загрузка данных из двоичных файлов')
def load_data(file, shape = None):
with open(file, 'rb') as r_b:
data = np.fromfile(r_b)
if shape is not None:
size = len(data)
if len(shape) == 2:
size = int(size / (shape[0] * shape[1]))
data = data.reshape(size, shape[0], shape[1])
else:
size = int(size / shape[0])
data = data.reshape(size, shape[0])
return data
vrts = load_data('vrts.bin', [4, 3])
vrts_top = load_data('vrts_top.bin', [3])
nrms = load_data('nrms.bin', [3])
nrm_top = load_data('nrm_top.bin', None)
textr = load_data('textr.bin', [2])
textr_top = load_data('textr_top.bin', [2])
else:
hp = hp0
for i in range(ch): # Вершины
al = 0 # Первая вершина лежит на оси Х
s = ac * math.sqrt(hp)
h0 = hp
hp += dh
s2 = ac * math.sqrt(hp)
for j in range(n):
co = math.cos(al)
si = math.sin(al)
al += dal
co2 = math.cos(al)
si2 = math.sin(al)
# Координаты вершин очередной трапеции
v0 = np.array([s * co, h0, -s * si])
v1 = np.array([s * co2, h0, -s * si2])
v2 = np.array([s2 * co2, hp, -s2 * si2])
v3 = np.array([s2 * co, hp, -s2 * si])
vrts.append([v0, v1, v2, v3])
a = v1 - v0
b = v3 - v0
sab = np.cross(a, b) # Векторное произведение
sab = sab / np.linalg.norm(sab) # Нормализация
#sab = sab / np.sqrt(np.sum(sab**2))
nrms.append(sab) # Координаты нормали
textr.append([j * dnx, (h0 - hp0) / h_cover]) # Координаты текстуры
n_vrts = len(vrts)
# Крышка
al = 0
kt = 0.25
for j in range(n):
co = math.cos(al); si = math.sin(al)
al += dal
vrts_top.append([s2 * co, hp, -s2 * si])
nrms.append(nrms[n_vrts - n + j])
textr.append([j * dnx, 1])
if texFromFile:
j2 = 2 * j * dnx
if j <= n / 4:
textr_top.append([j2, 0.5 - j2])
elif j <= n / 2:
textr_top.append([j2, j2 - 0.5])
elif j <= 3 * n / 4:
textr_top.append([2 - j2, j2 - 0.5])
else:
textr_top.append([2 - j2, 2.5 - j2])
else:
textr_top.append([kt * co, kt * si])
v0 = np.array(vrts_top[0])
v1 = np.array(vrts_top[1])
vn = np.array(vrts_top[n - 1])
nrm_top = np.cross(v1 - v0, vn - v0) # Нормаль к крышке
nrm_top = nrm_top / np.linalg.norm(sab)
if save_to_file:
print('Запись данных в двоичные файлы')
def write_to_bin(file, data):
fn = open(file, 'wb')
fn.write(np.array(data))
fn.close()
write_to_bin('vrts.bin', vrts)
write_to_bin('vrts_top.bin', vrts_top)
write_to_bin('nrms.bin', nrms)
write_to_bin('nrm_top.bin', nrm_top)
write_to_bin('textr.bin', textr)
write_to_bin('textr_top.bin', textr_top)
if plot_surf:
from mpl_toolkits.mplot3d import Axes3D # Для projection = '3d'
from matplotlib import cm
import matplotlib.pyplot as plt
xy, z = [], []
x_min = x_max = vrts[0][0][0]
y_min = y_max = vrts[0][0][2]
for quad in vrts:
for v in quad:
p = [v[0], v[2]]
if not p in xy:
xy.append(p)
z.append(v[1])
if p[0] < x_min: x_min = p[0]
if p[0] > x_max: x_max = p[0]
if p[1] < y_min: y_min = p[1]
if p[1] > y_max: y_max = p[1]
step = 0.5
X = np.arange(x_min, x_max, step) # Формирование сетки
Y = np.arange(y_min, y_max, step)
X, Y = np.meshgrid(X, Y)
Z = ac*X**2 + ac*Y**2 # Формируем массив Z формы (len(X), len(Y))
fig = plt.figure()
ax = fig.gca(projection = '3d')
surf = ax.plot_surface(X, Y, Z, cmap = cm.plasma) # plasma Spectral
ax.set_xlabel('X') # Метки осей координат
ax.set_ylabel('Y')
ax.set_zlabel('Z')
for label in ax.xaxis.get_ticklabels(): # Настройка оси X
label.set_color('black')
label.set_rotation(-45)
label.set_fontsize(9)
for label in ax.yaxis.get_ticklabels(): # Настройка оси Y
label.set_fontsize(9)
for label in ax.zaxis.get_ticklabels(): # Настройка оси Z
label.set_fontsize(9)
ax.view_init(elev = 30, azim = 45) # Проецирование
fig.colorbar(surf, shrink = 0.5, aspect = 5) # Шкала цветов
plt.show() # Отображение результата
exit()
#
def c_float_Array(data): # Преобразование в си-массив
return (gl.GLfloat * len(data))(*data)
lghtClr0 = [0.75, 0, 0, 0]
mtClr = c_float_Array([1, 1, 0, 0])
light_position = c_float_Array([-80, 20, 90, 0])
lghtClr = c_float_Array([0.75, 0, 0, 0])
#
def texInit():
if texFromFile:
fn = 'G:\\python\\openGL\\кот.jpg'
img = pyglet.image.load(fn)
iWidth = img.width
iHeight = img.height
img = img.get_data('RGB', iWidth * 3)
else:
iWidth = iHeight = 64
n = 3 * iWidth * iHeight
img = np.zeros((3, iWidth, iHeight), dtype = 'uint8')
for i in range(iHeight): # Генерация черно-белого образа, на основе которого создается текстура
for j in range(iWidth):
img[:, i, j] = ((i - 1) & 16 ^ (j - 1) & 16) * 255
img = img.reshape(n)
img = (gl.GLubyte * n)(*img)
p = gl.GL_TEXTURE_2D
r = gl.GL_RGB
gl.glTexParameterf(p, gl.GL_TEXTURE_WRAP_S, gl.GL_REPEAT)
gl.glTexParameterf(p, gl.GL_TEXTURE_WRAP_T, gl.GL_REPEAT)
gl.glTexParameterf(p, gl.GL_TEXTURE_MAG_FILTER, gl.GL_LINEAR)
gl.glTexParameterf(p, gl.GL_TEXTURE_MIN_FILTER, gl.GL_LINEAR)
gl.glTexEnvf(gl.GL_TEXTURE_ENV, gl.GL_TEXTURE_ENV_MODE, gl.GL_DECAL)
gl.glTexImage2D(p, 0, r, iWidth, iHeight, 0, r, gl.GL_UNSIGNED_BYTE, img)
if use_txtr:
gl.glEnable(p)
w = h = h_cover
width, height = 20 * w, 10 * w
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Параболоид')
gl.glClearColor(1, 1, 1, 1) # Белый цвет фона
gl.glClear(gl.GL_COLOR_BUFFER_BIT|gl.GL_DEPTH_BUFFER_BIT)
gl.glPolygonMode(gl.GL_FRONT_AND_BACK, gl.GL_FILL)
gl.glLineWidth(2)
gl.glPointSize(4)
gl.glEnable(gl.GL_POINT_SMOOTH)
gl.glShadeModel(gl.GL_SMOOTH) # GL_SMOOTH, GL_FLAT - без интерполяции цветов
gl.glCullFace(gl.GL_BACK) # Запрещен вывод граней, показанных нелицевой стороной
gl.glEnable(gl.GL_CULL_FACE) # Активизируем режим GL_CULL_FACE
##gl.glEnable(gl.GL_NORMALIZE)
if show_normals:
gl.glEnable(gl.GL_DEPTH_TEST) # Активизируем тест глубины
texInit()
@window.event
def on_draw():
window.clear()
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-w, w, -0.5 * h, h, -w, w) # Ортографическое проецирование
gl.glRotatef(30, 1, 0, 0) # Поворот относительно оси X
if use_txtr and texFromFile:
gl.glRotatef(90, 0, 1, 0) # Поворот относительно оси Y
gl.glTranslatef(0, -7, 0) # Перенос объекта вниз (вдоль оси Y)
gl.glMaterialfv(gl.GL_FRONT, gl.GL_SPECULAR, mtClr)
gl.glLightfv(gl.GL_LIGHT0, gl.GL_POSITION, light_position)
gl.glLightfv(gl.GL_LIGHT0, gl.GL_SPECULAR, lghtClr)
gl.glEnable(gl.GL_LIGHTING) # Активизируем заданные параметры освещенности
gl.glEnable(gl.GL_LIGHT0)
gl.glBegin(gl.GL_QUADS)
k = -1
for i in range(ch):
for j in range(n):
k += 1
v = vrts[k]
v0 = v[0]; v1 = v[1]; v2 = v[2]; v3 = v[3]
sn = nrms[k] # Нормаль к вершине (она же нормаль к грани)
gl.glNormal3f(sn[0], sn[1], sn[2])
tc = textr[k] # Координаты текстуры
gl.glTexCoord2f(tc[0], tc[1])
gl.glVertex3f(v0[0], v0[1], v0[2])
sn = nrms[k + 1]
gl.glNormal3f(sn[0], sn[1], sn[2])
gl.glTexCoord2f(tc[0] + dnx, tc[1])
gl.glVertex3f(v1[0], v1[1], v1[2])
sn = nrms[k + n]
gl.glNormal3f(sn[0], sn[1], sn[2])
gl.glTexCoord2f(tc[0] + dnx, tc[1] + dny)
gl.glVertex3f(v2[0], v2[1], v2[2])
sn = nrms[k + n - 1]
gl.glNormal3f(sn[0], sn[1], sn[2])
gl.glTexCoord2f(tc[0], tc[1] + dny)
gl.glVertex3f(v3[0], v3[1], v3[2])
gl.glEnd() # Заканчиваем вывод боковых граней
if show_top:
gl.glBegin(gl.GL_POLYGON) # Вывод крышки
gl.glNormal3f(nrm_top[0], nrm_top[1], nrm_top[2]) # Нормаль к крышке
for j in range(n):
v = vrts_top[j]
tc = textr_top[j]
gl.glTexCoord2f(tc[0], tc[1])
gl.glVertex3f(v[0], v[1], v[2])
gl.glEnd() # Заканчиваем вывод крышки
if show_normals:
# Вывод нормалей
gl.glDisable(gl.GL_LIGHTING) # Отключаем расчет освещенности
gl.glLineWidth(2) # Задание толщины линии
gl.glColor3f(0, 0, 0) # Задание текущего цвета
gl.glBegin(gl.GL_LINES)
k = -1
for i in range(ch):
for j in range(n):
k += 1
v = vrts[k][0]
gl.glVertex3f(v[0], v[1], v[2])
sn = nrms[k]
sx = kn * sn[0]
sy = kn * sn[1]
sz = kn * sn[2]
gl.glVertex3f(v[0] + sx, v[1] + sy, v[2] + sz)
# Нормали в верхнем сечении совпадают с нормалями в предыдущем сечении
if i == ch - 1:
v = vrts[k][3]
gl.glVertex3f(v[0], v[1], v[2])
gl.glVertex3f(v[0] + sx, v[1] + sy, v[2] + sz)
gl.glEnd()
if show_top:
gl.glColor3f(1, 1, 1) # Текущий цвет
gl.glBegin(gl.GL_LINES) # Нормаль к крышке
gl.glVertex3f(0, h_cover, 0)
gl.glVertex3f(kn * nrm_top[0], h_cover + kn * nrm_top[1], kn * nrm_top[2])
gl.glEnd()
@window.event
def on_key_press(symbol, modifiers):
if symbol == key._1:
gl.glDisable(gl.GL_TEXTURE_2D)
gl.glPolygonMode(gl.GL_FRONT, gl.GL_FILL)
gl.glShadeModel(gl.GL_SMOOTH)
gl.glEnable(gl.GL_CULL_FACE)
elif symbol == key._2:
gl.glPolygonMode(gl.GL_FRONT, gl.GL_FILL)
gl.glShadeModel(gl.GL_FLAT)
gl.glEnable(gl.GL_CULL_FACE)
elif symbol == key._3:
gl.glPolygonMode(gl.GL_FRONT, gl.GL_LINE) # Вывод ребер
elif symbol == key._4:
gl.glPolygonMode(gl.GL_FRONT, gl.GL_POINT)
elif symbol == key._5:
gl.glDisable(gl.GL_CULL_FACE)
app.run()
Сведения о созданной модели будут записаны в бинарные файлы, если
save_to_file = True
и
read_from_file = False
Если read_from_file = True, то модель будет прочитана из ранее созданных бинарных файлов.
Если plot_surf = True, то по уравнению параболоида будет выведена его поверхность (рис. 19).
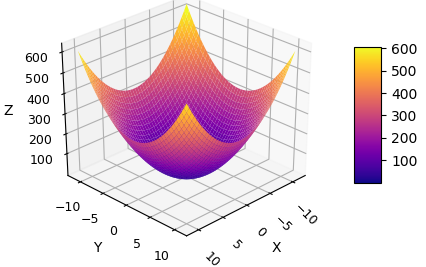
Рис. 19. Параболоид
Рассматривается на примере вывода игральной кости (рис. 20).
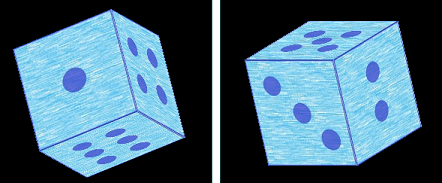
Рис. 20. Используется 6 текстур
Текстуры создаются на основе 6 файлов, содержащих приведенные на рис. 21 изображения.

Рис. 21. Стороны игральной кости
Помимо куба с текстурами, приводимая ниже программа показывает после нажатия на клавиши 2-6 разные способы вывода куба (рис. 22).
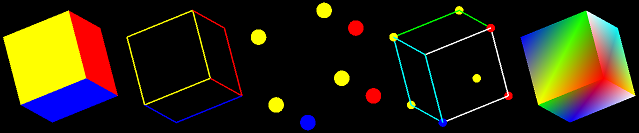
Рис. 22. После нажатия на 2, 3, ..., 6
После нажатия на 1 возвращаемся к игральной кости (рис. 20). После нажатия на 4 растут размеры точек в вершинах куба до тех пор, пока не достигнут максимально возможного значения:
elif symbol == key._4:
ps = (gl.GLfloat * 1)()
ps_range = (gl.GLfloat * 2)()
gl.glGetFloatv(gl.GL_POINT_SIZE, ps) # Получаем текущий размер точки
# Допустимый диапазон изменения размеров точки
gl.glGetFloatv(gl.GL_POINT_SIZE_RANGE, ps_range)
ps = ps[0]
ps = (ps + 2) if ps < ps_range[1] - 2 else 4
gl.glPointSize(ps)
gl.glPolygonMode(gl.GL_FRONT, gl.GL_POINT)
Программа вывода куба с текстурой и без нее:
# Игральная кость
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window, key
h = 20 # Половины длины ребра куба
w = 2 * h # Для задания области вывода
width = height = 300 # Размер окна вывода
textureIDs = (gl.GLuint * 6)() # Массив идентификаторов (номеров) текстур
p = gl.GL_TEXTURE_2D
tc = 1 # Число повторов текстуры
rot_x = 15 # Углы поворота вокруг осей X, Y и Z
rot_y = 25 # (15, 25, 15) или (-25, 215, -15)
rot_z = 15
verts = ((h, -h, -h), # <class 'tuple'> Координаты вершин куба
(h, h, -h),
(-h, h, -h),
(-h, -h, -h),
(h, -h, h),
(h, h, h),
(-h, -h, h),
(-h, h, h))
faces = ((0, 1, 2, 3), # Индексы вершин граней куба
(3, 2, 7, 6),
(6, 7, 5, 4),
(4, 5, 1, 0),
(1, 5, 7, 2),
(4, 0, 3, 6))
clrs = ((1, 0, 0), (0, 1, 0), (0, 0, 1), (1, 1, 0),
(0, 1, 1), (1, 1, 1), (1, 0, 0), (0, 1, 0),
(0, 0, 1), (1, 1, 0), (0, 1, 1), (1, 1, 1))
t_coords = ((0, 0), (0, tc), (tc, tc), (tc, 0)) # Координаты текстуры
# Индексы ребер куба (используется при выводе линий вдоль ребер куба)
edges = ((0, 1), (0, 3), (0, 4), (2, 1), (2, 3), (2, 7),
(6, 3), (6, 4), (6, 7), (5, 1), (5, 4), (5, 7))
def texInit(): # Формирование текстур
gl.glGenTextures(6, textureIDs)
r = gl.GL_RGB
p3 = gl.GL_REPEAT # GL_REPEAT GL_CLAMP_TO_EDGE
p4 = gl.GL_LINEAR
for k in range(6):
fn = 'dice' + str(k) + '.jpg'
img = pyglet.image.load(fn)
iWidth = img.width
iHeight = img.height
img = img.get_data('RGB', iWidth * 3)
gl.glBindTexture(p, textureIDs[k])
gl.glTexParameterf(p, gl.GL_TEXTURE_WRAP_S, p3)
gl.glTexParameterf(p, gl.GL_TEXTURE_WRAP_T, p3)
gl.glTexParameterf(p, gl.GL_TEXTURE_MAG_FILTER, p4)
gl.glTexParameterf(p, gl.GL_TEXTURE_MIN_FILTER, p4)
gl.glTexEnvf(gl.GL_TEXTURE_ENV, gl.GL_TEXTURE_ENV_MODE, gl.GL_DECAL)
gl.glTexImage2D(p, 0, r, iWidth, iHeight, 0, r, gl.GL_UNSIGNED_BYTE, img)
gl.glEnable(p)
def cube_draw():
k = -1
for face in faces:
k += 1
m = -1
v4, c4, t4 = (), (), ()
gl.glBindTexture(p, textureIDs[k])
for v in face:
m += 1
c4 += clrs[k + m]
t4 += t_coords[m]
v4 += verts[v]
graphics.draw(4, gl.GL_QUADS, ('v3f', v4), ('c3f', c4), ('t2f', t4))
## gl.glColor3f(1, 0, 0)
## for edge in edges:
## v2 = ()
## for v in edge:
## v2 += verts[v]
## graphics.draw(2, gl.GL_LINES, ('v3f', v2))
#
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Куб')
gl.glClearColor(0, 0, 0, 1) # Черный цвет фона
gl.glClear(gl.GL_COLOR_BUFFER_BIT|gl.GL_DEPTH_BUFFER_BIT)
gl.glPolygonMode(gl.GL_FRONT, gl.GL_FILL)
gl.glPolygonMode(gl.GL_BACK, gl.GL_LINE)
gl.glLineWidth(3)
gl.glPointSize(4)
gl.glEnable(gl.GL_POINT_SMOOTH)
gl.glShadeModel(gl.GL_SMOOTH) # GL_SMOOTH, GL_FLAT
gl.glCullFace(gl.GL_BACK) # GL_FRONT GL_BACK
gl.glEnable(gl.GL_CULL_FACE)
gl.glEnable(gl.GL_DEPTH_TEST)
gl.glDepthFunc(gl.GL_LESS) # GL_LESS GL_GREATER
#
texInit() # Создаем текстуры
#
@window.event
def on_draw():
window.clear()
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-w, w, -w, w, -w, w)
gl.glRotatef(rot_x, 1, 0, 0) # Поворот относительно оси X
gl.glRotatef(rot_y, 0, 1, 0) # Поворот относительно оси Y
gl.glRotatef(rot_z, 0, 0, 1) # Поворот относительно оси Z
cube_draw()
@window.event
def on_key_press(symbol, modifiers):
if symbol == key._1:
gl.glPolygonMode(gl.GL_FRONT, gl.GL_FILL)
gl.glShadeModel(gl.GL_SMOOTH)
gl.glEnable(gl.GL_CULL_FACE)
gl.glEnable(p)
elif symbol == key._2:
gl.glPolygonMode(gl.GL_FRONT, gl.GL_FILL)
gl.glShadeModel(gl.GL_FLAT)
gl.glEnable(gl.GL_CULL_FACE)
gl.glDisable(p)
elif symbol == key._3:
gl.glPolygonMode(gl.GL_FRONT, gl.GL_LINE) # Вывод ребер
elif symbol == key._4:
ps = (gl.GLfloat * 1)()
ps_range = (gl.GLfloat * 2)()
gl.glGetFloatv(gl.GL_POINT_SIZE, ps) # Получаем текущий размер точки
# Допустимый диапазон изменения размеров точки
gl.glGetFloatv(gl.GL_POINT_SIZE_RANGE, ps_range)
ps = ps[0]
ps = (ps + 2) if ps < ps_range[1] - 2 else 4
gl.glPointSize(ps)
gl.glPolygonMode(gl.GL_FRONT, gl.GL_POINT)
elif symbol == key._5:
gl.glDisable(gl.GL_CULL_FACE)
elif symbol == key._6:
gl.glPolygonMode(gl.GL_FRONT, gl.GL_FILL)
gl.glShadeModel(gl.GL_SMOOTH)
gl.glEnable(gl.GL_CULL_FACE)
gl.glDisable(p)
app.run()
Выводится вращающаяся игральная кость.
Шаг угла поворота 1°
Шаг угла поворота вокруг каждой оси равен либо da, либо -da.
Смена знака шага da выполняется после заданного числа поворотов (в программе – это 180).
Процедура cube_draw, выводящая куб, вызывается после каждого срабатывания таймера:
pyglet.clock.tick()
Вызов обеспечивает метод schedule:
pyglet.clock.schedule(cube_draw)
# Вращающаяся кость
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window
n_rot, da = 0, 1
h = 20 # Половины длины ребра куба
w = 2 * h # Для задания области вывода
width = height = 300 # Размер окна вывода
textureIDs = (gl.GLuint * 6)() # Массив идентификаторов (номеров) текстур
p = gl.GL_TEXTURE_2D
tc = 1 # Число повторов текстуры
verts = ((h, -h, -h), # Координаты вершин куба
(h, h, -h),
(-h, h, -h),
(-h, -h, -h),
(h, -h, h),
(h, h, h),
(-h, -h, h),
(-h, h, h))
faces = ((0, 1, 2, 3), # Индексы вершин граней куба
(3, 2, 7, 6),
(6, 7, 5, 4),
(4, 5, 1, 0),
(1, 5, 7, 2),
(4, 0, 3, 6))
t_coords = ((0, 0), (0, tc), (tc, tc), (tc, 0)) # Координаты текстуры
def texInit(): # Формирование текстур
gl.glGenTextures(6, textureIDs)
r = gl.GL_RGB
p3 = gl.GL_REPEAT
p4 = gl.GL_LINEAR
for k in range(6):
fn = 'dice' + str(k) + '.jpg'
img = pyglet.image.load(fn)
iWidth = img.width
iHeight = img.height
img = img.get_data('RGB', iWidth * 3)
gl.glBindTexture(p, textureIDs[k])
gl.glTexParameterf(p, gl.GL_TEXTURE_WRAP_S, p3)
gl.glTexParameterf(p, gl.GL_TEXTURE_WRAP_T, p3)
gl.glTexParameterf(p, gl.GL_TEXTURE_MAG_FILTER, p4)
gl.glTexParameterf(p, gl.GL_TEXTURE_MIN_FILTER, p4)
gl.glTexEnvf(gl.GL_TEXTURE_ENV, gl.GL_TEXTURE_ENV_MODE, gl.GL_DECAL)
gl.glTexImage2D(p, 0, r, iWidth, iHeight, 0, r, gl.GL_UNSIGNED_BYTE, img)
gl.glEnable(p)
def cube_draw(dt):
k = -1
for face in faces:
k += 1
m = -1
v4, t4 = (), ()
gl.glBindTexture(p, textureIDs[k])
for v in face:
m += 1
t4 += t_coords[m]
v4 += verts[v]
graphics.draw(4, gl.GL_QUADS, ('v3f', v4), ('t2f', t4))
window = Window(visible = True, width = width, height = height,
resizable = True, caption = 'Куб')
gl.glClearColor(0, 0, 0, 1) # Черный цвет фона
gl.glClear(gl.GL_COLOR_BUFFER_BIT)
gl.glCullFace(gl.GL_BACK) # GL_FRONT GL_BACK
gl.glEnable(gl.GL_CULL_FACE)
#
texInit() # Создаем текстуры
#
@window.event
def on_draw():
global n_rot, da
window.clear()
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-w, w, -w, w, -w, w)
gl.glMatrixMode(gl.GL_MODELVIEW)
if n_rot > 180:
n_rot = 0
da = -da
n_rot += 1
gl.glRotatef(da, 1, 0, 0)
gl.glRotatef(da, 0, 1, 0)
gl.glRotatef(da, 0, 0, 1)
pyglet.clock.tick()
#
pyglet.clock.schedule(cube_draw)
app.run()
На рис. 23 показаны два прямоугольника с одинаковыми размерами, но разными z-координатами вершин: z-координата вершин красного прямоугольника (КП) равна 1, синего прямоугольника (СП) – 0.

Рис. 23. Тест глубины отключен
СП перекрывает КП, хотя z-координата вершин КП больше, чем у СП (1 против 0). То есть должно быть ровно наоборот: КП перекрывает СП.
Однако этого не происходит, поскольку в приводимой ниже программе, выводящей СП и КП, первоначально отключен тест глубины:
glDisable(GL_DEPTH_TEST),
а СП выводится вслед за КП.
При нажатии на 1 включается тест глубины:
glEnable(GL_DEPTH_TEST),
и вывод осуществляется с учетом z-координат вершин СП и КП (рис. 24).

Рис. 24. Выполняется тест глубины
При нажатии на 2 тест глубины отключается и получаем рис. 23.
# Тест глубины
import pyglet
from pyglet import app, gl, graphics
from pyglet.window import Window, key
d = 20 # Половина длины большой стороны прямоугольника
d2 = d / 2
z2 = 1 # z-координата вершин красного прямоугольника
wx, wy = 2 * d, 2 * d2 # Для задания области вывода
width, height = 300, 150 # Размеры окна вывода
def draw():
gl.glMatrixMode(gl.GL_PROJECTION)
gl.glLoadIdentity()
gl.glOrtho(-wx, wx, -wy, wy, -2, 2)
gl.glMatrixMode(gl.GL_MODELVIEW)
gl.glLoadIdentity()
gl.glTranslatef(-d/2, -d2/2, 0)
gl.glColor3f(1, 0, 0) # Вывод красного прямоугольника (КП)
graphics.draw(4, gl.GL_QUADS, ('v3f', (-d, -d2, z2, d, -d2, z2, d, d2, z2, -d, d2, z2)))
gl.glTranslatef(d, d2, 0)
gl.glColor3f(0, 0, 1) # Вывод синего прямоугольника (СП)
graphics.draw(4, gl.GL_QUADS, ('v2f', (-d, -d2, d, -d2, d, d2, -d, d2)))
#
window = Window(width = width, height = height, caption = 'Тест глубины')
gl.glClearColor(0.75, 0.75, 0.75, 1) # Серый цвет фона
gl.glClear(gl.GL_COLOR_BUFFER_BIT|gl.GL_DEPTH_BUFFER_BIT)
gl.glDisable(gl.GL_DEPTH_TEST)
gl.glDepthFunc(gl.GL_LESS) # GL_LESS GL_GREATER
#
@window.event
def on_draw():
window.clear()
draw()
@window.event
def on_key_press(symbol, modifiers):
if symbol == key._1:
gl.glEnable(gl.GL_DEPTH_TEST)
elif symbol == key._2:
gl.glDisable(gl.GL_DEPTH_TEST)
app.run()
На рис. 25 показан результат применения двух материалов и двух источников света.
Первые материал и источник света применяются к левому прямоугольнику, вторые – к правому.

Рис. 25. Два материала и источника света. Нормали рассчитаны к граням
При левая грань выведена с применением первой пары материала и источника света:
gl.glMaterialfv(gl.GL_FRONT, gl.GL_SPECULAR, mtClr)
gl.glEnable(gl.GL_LIGHT0)
gl.glDisable(gl.GL_LIGHT1)
правая – с применением второй пары материала и источника света:
gl.glMaterialfv(gl.GL_FRONT, gl.GL_SPECULAR, mtClr2)
gl.glDisable(gl.GL_LIGHT0)
gl.glEnable(gl.GL_LIGHT1)
Цвета первых материала и света соответственно
[0.7, 0.9, 0, 0] и [1, 0.5, 0.5, 0],
а вторых
[0, 0.7, 0.9, 0] и [0.5, 0.5, 1.0, 0].
Координаты первого и второго источников света соответственно
[-100, 200, 400, 0] и [100, 200, 400, 0].
При одновременной работе обоих источников света получаем рис. 26.

Рис. 26. Два материала и источника света. Включены оба источника
Прозрачность моделируется, если активизирован режим смешения цветов
glEnable(GL_BLEND)
и функция смешения цветов задана следующим образом:
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
Степень прозрачности регулируется последним компонентом RGBA, например, при задании цвета материала:
mt_clr0 = [1, 0, 0, 0.45] # Цвет материала
Прозрачность растет по мере уменьшения A-компонента цвета.
Тест глубины при имитации прозрачности следует отключить.
Пример:
# Смешение цветов (прозрачность) и тест глубины
from pyglet.gl import *
from pyglet import app, graphics
from pyglet.window import Window, key
d = 20 # Половина длины большой стороны прямоугольника
d2 = d / 2
z0 = 3
z1 = 1
z2 = 2
wx, wy = 2 * d, 2 * d2 # Для задания области вывода
width, height = 300, 150 # Размеры окна вывода
mt_clr0 = (GLfloat * 4)(*[1, 0, 0, 0.75])
mt_clr1 = (GLfloat * 4)(*[0, 1, 0, 0.5])
mt_clr2 = (GLfloat * 4)(*[0, 0, 1, 0.5])
light_position = (GLfloat * 4)(*[0, 40, 40, 0])
lght_clr = (GLfloat * 4)(*[1, 1, 1, 1])
def material(mt_clr):
glMaterialfv(GL_FRONT, GL_SPECULAR, mt_clr)
glMaterialfv(GL_FRONT, GL_DIFFUSE, mt_clr)
glMaterialfv(GL_FRONT, GL_AMBIENT, mt_clr)
def rect(mt_clr, verts):
material(mt_clr)
graphics.draw(4, GL_QUADS, ('v3f', verts),
('n3f', (0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1)))
def draw():
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
glOrtho(-wx, wx, -wy, wy, -5, 5)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
glLightfv(GL_LIGHT0, GL_POSITION, light_position)
rect(mt_clr0, (-d, -d2, z0, d, -d2, z0, d, d2, z0, -d, d2, z0))
glTranslatef(3*d/4, 3*d2/4, 0)
rect(mt_clr1, (-d, -d2, z1, d, -d2, z1, d, d2, z1, -d, d2, z1))
glTranslatef(-3*d/2, -3*d2/2, 0)
rect(mt_clr2, (-d, -d2, z2, d, -d2, z2, d, d2, z2, -d, d2, z2))
#
window = Window(width = width, height = height, resizable = True, caption = 'Смешение цветов')
glClearColor(1, 1, 1, 1)
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT)
glDisable(GL_DEPTH_TEST)
glDepthFunc(GL_LESS) # GL_LESS GL_GREATER
glEnable(GL_LIGHTING)
glEnable(GL_LIGHT0)
glLightfv(GL_LIGHT0, GL_SPECULAR, lght_clr)
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
glEnable(GL_BLEND)
#
@window.event
def on_draw():
window.clear()
draw()
@window.event
def on_key_press(symbol, modifiers):
if symbol == key._1:
if modifiers == key.MOD_CTRL:
glDisable(GL_BLEND)
else:
glEnable(GL_BLEND)
elif symbol == key._2:
if modifiers == key.MOD_CTRL:
glDisable(GL_DEPTH_TEST)
else:
glEnable(GL_DEPTH_TEST)
app.run()
Результат:
| Рисунок | GL_BLEND | GL_DEPTH_TEST |
|---|---|---|
 | Да | Нет |
 | Да | Да |
 | Нет | Нет |
 | Нет | Да |
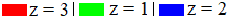 | glDepthFunc(GL_LESS) | |
В первом примере выводится приведенная на рис. 27 картинка.
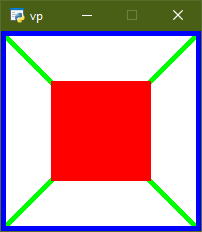
Рис. 27. Растровая картинка
Это выполняет следующий код:
import numpy as np
from pyglet.gl import *
from pyglet.window import Window
from pyglet import app
w = 200
vp = np.full((w, w, 3), 255, dtype = 'uint8')
for i in range(w):
i0, i2 = i - 2, i + 2
vp[i0:i2, i0:i2] = [0, 255, 0]
i00, i20 = w - i0 - 1, w - i2 - 1
vp[i0:i2, i20:i00] = [0, 255, 0]
vp[-5:, :] = vp[:5, :] = [0, 0, 255]
vp[:, -5:] = vp[:, :5] = [0, 0, 255]
k = w // 4; k2 = 3 * k
vp[k:k2, k:k2] = [255, 0, 0]
vp = vp.flatten()
vp = (GLubyte * (w * w * 3))(*vp)
window = Window(visible = True, width = w, height = w, caption = 'vp')
@window.event
def on_draw():
window.clear()
glDrawPixels(w, w, GL_RGB, GL_UNSIGNED_BYTE, vp)
app.run()
Во втором примере данные типа uint8 накапливаются в двумерном массиве vp. Они отображают распределение температуры на пластине, получаемое в результате решения краевой задачи. Массив vp содержит оттенки серого цвета: чем больше значение, тем выше температура. Перед отображением они преобразуются в RGB таким образом, что по мере снижения температуры цвет переходит от красного в синий. Это обеспечивает следующий код:
# (w, w) – форма массива vp
vp2 = np.zeros((w, w, 3), dtype = 'uint8')
for i in range(w):
for j in range(w):
clr = vp[i, j]
if clr > 240:
clr2 = (0xFF, 0, 0) # Red
elif clr > 225:
clr2 = (0xA5, 0xA2, 0x2A) # Brown
elif clr > 210:
clr2 = (0xFF, 0x63, 0x47) # Tomato
elif clr > 195:
clr2 = (0xFA, 0x80, 0x72) # Salmon
elif clr > 180:
clr2 = (0x7B, 0x68, 0xEE) # MediumSlateBlue
elif clr > 165:
clr2 = (0xFF, 0xFF, 0) # Yellow
elif clr > 145:
clr2 = (0xFF, 0xEF, 0xD5) # PapayaWhip
elif clr > 125:
clr2 = (0xEE, 0x82, 0xEE) # Violet
elif clr > 105:
clr2 = (0xDB, 0x70, 0x93) # PaleVioletRed
elif clr > 90:
clr2 = (0x9A, 0xCD, 0x32) # YellowGreen
elif clr > 75:
clr2 = (0, 255, 0) # Green
elif clr > 60:
clr2 = (0, 0xFF, 0x7F) # SpringGreen
elif clr > 50:
clr2 = (0, 0xFA, 0x9A) # MediumSpringGreen
elif clr > 40:
clr2 = (0x3C, 0xB3, 0x71) # MediumSeaGreen
elif clr > 30:
clr2 = (0x46, 0x82, 0xB4) # SteelBlue
elif clr > 20:
clr2 = (0x41, 0x69, 0xE1) # RoyalBlue
elif clr > 10:
clr2 = (0, 0, 255) # Blue
else:
clr2 = (0, 0, 0xCD) # MediumBlue
vp2[j, i, :] = clr2
Предварительно массив vp масштабируется (каждое его значение повторяется z_val раз):
from scipy.ndimage import zoom
if z_val > 1: vp = zoom(vp, z_val)
Отображение массива средствами OpenGL:
vp = (GLubyte * len(vp))(*vp)
window = Window(visible = True, width = w, height = w, caption = ('nH = ' + str(nH))) # nH – число нагревателей
@window.event
def on_draw():
window.clear()
glDrawPixels(w, w, GL_RGB, GL_UNSIGNED_BYTE, vp)
app.run()
Результат (рис. 28):
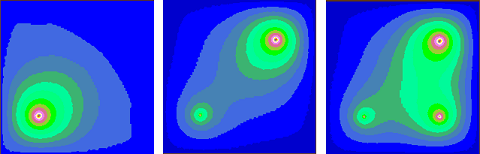
Рис. 28. Пластина с одним, двумя и тремя нагревателями
Процесс вычислений иллюстрирует следующее видео:
Предварительно для его получения формируются файлы с картами температур пластины после 10, 20, ..., 100 шагов вычислений. Далее они воспроизводятся в результате выполнения следующего кода:
from pyglet import clock
def callback(dt):
global vp, n_f
n_f += 1
if n_f > 10: n_f = 1
fn = fn0 + str(n_f) + '.bin'
vp = load_data(fn)
vp = (GLubyte * len(vp))(*vp)
clock.schedule_interval(callback, 1.5)
n_f = 1
fn = fn0 + str(n_f) + '.bin'
vp = load_data(fn)
vp = (GLubyte * len(vp))(*vp)
window = Window(visible = True, width = w, height = w, caption = ('nH = ' + str(nH)))
@window.event
def on_draw():
window.clear()
glDrawPixels(w, w, GL_RGB, GL_UNSIGNED_BYTE, vp)
app.run()
Через заданный интервал процедура callback загружает очередной файл с данными, который затем отображается в окне вывода OpenGL, заменяя прежнее изображение на новое.
Полный код решения краевой задачи, сохранения, загрузки и отображения данных:
import numpy as np, time
# 1 - решение и запись карты цветов в файл или несколько файлов
# 2 - отображение файлов
step = 2
nH = 2 # Число нагревателей (не более трех)
gl = True # Использование OpenGL
many_files = not True # Режим анимации
if not gl: many_files = False
n = 100 # Размер сетки
n1 = n + 1
n2 = n + 2
if gl:
from pyglet.gl import *
from pyglet import app, graphics
from pyglet.window import Window, key
from scipy.ndimage import zoom
z_val = 2
else:
from matplotlib import pyplot as plt
z_val = 1
w = n2 * z_val
g = 4 # Температура на границе
eps = 0.5 # Точность: eps = pow(10, -2)
tH, tH2, tH3 = 60, 140, 100 # Температуры нагревателей 1, 2 и 3
# Координаты нагревателей 1, 2 и 3
# Должны находиться в узлах сетки
xH, yH = n // 4, n // 4
xH2, yH2 = 3 * n // 4, 3 * n // 4
xH3, yH3 = xH2, yH
u = np.zeros((n2, n2), dtype = 'float32')
u_prev = np.zeros((n2, n2), dtype = 'float32')
vp = np.zeros((n2, n2), dtype = 'uint8')
max_steps = 100
fn0 = 'vp' + str(nH) + ('gl' if gl else '')
fn = fn0 + '.bin'
def save_data(fn, data):
fp = open(fn, 'wb')
fp.write(data.flatten())
fp.close()
def load_data(fn):
with open(fn, 'rb') as f:
data = np.fromfile(f, dtype = np.uint8)
return data
def f_r(x, y): # Правая часть
prs = 0.1
if abs(x - xH) < prs and abs(y - yH) < prs: return tH
if abs(x - xH2) < prs and abs(y - yH2) < prs and nH > 1: return tH2
if abs(x - xH3) < prs and abs(y - yH3) < prs and nH > 2: return tH3
return 0
def maxSumAMinusB(a, b):
max_val = -np.inf
for i in range(1, n1):
max_val = max(max_val, np.sum(abs(a[i, 1:n1] - b[i, 1:n1])))
return max_val
def sumAMultB(a, b):
return np.sum(a[1:n1, 1:n1] * b[1:n1, 1:n1])
def grid():
u[:, 0] = g; u[:, n1] = g
u[0, :] = g; u[n1, :] = g
def solve(vp):
r = np.zeros((n1, n1), dtype = 'float32')
r_prev = np.zeros((n1, n1), dtype = 'float32')
ap = np.zeros((n1, n1), dtype = 'float32')
p = np.zeros((n2, n2), dtype = 'float32')
for i in range(1, n1):
for j in range(1, n1):
# Начальные невязки
up_ij2 = 2 * u[i, j]
r[i, j] = f_r(i, j) + (u[i + 1, j] - up_ij2 + u[i - 1, j]) + (u[i, j + 1] - up_ij2 + u[i, j - 1])
p[i, j] = r[i, j]
n_steps = m_val = n_f = 0
while(1):
for i in range(1, n1):
for j in range(1, n1):
u_prev[i, j] = u[i, j]
up_ij2 = 2 * p[i, j]
ap[i, j] = -(p[i + 1, j] - up_ij2 + p[i - 1, j]) - (p[i, j + 1] - up_ij2 + p[i, j - 1])
alpha = sumAMultB(r, r) / sumAMultB(ap, p)
u[1:n1, 1:n1] = u[1:n1, 1:n1] + alpha * p[1:n1, 1:n1] # Приближения
r_prev[1:, 1:] = r[1:, 1:]
r[1:, 1:] = r[1:, 1:] - alpha * ap[1:, 1:] # Невязки
betta = sumAMultB(r, r) / sumAMultB(r_prev, r_prev)
p[1:n1, 1:n1] = r[1:, 1:] + betta * p[1:n1, 1:n1]
# Сравнение текущего и предшествующего приближений на предмет достижения заданной точности
m_val = maxSumAMinusB(u, u_prev)
n_steps += 1
if many_files and n_steps % 10 == 0:
vp2 = make_map(vp)
n_f += 1
fn = fn0 + str(n_f) + '.bin'
save_data(fn, vp2)
if m_val < eps or n_steps >= max_steps: break
print('Число шагов. Предельное:', max_steps, 'Сделано:', n_steps, 'Достигнутая точность:', m_val)
def make_map(vp):
uMax = np.max(u)
vp[...] = 255 * u / uMax
if gl:
if z_val > 1: vp = zoom(vp, z_val)
vp2 = np.zeros((w, w, 3), dtype = 'uint8')
for i in range(w):
for j in range(w):
clr = vp[i, j]
if clr > 240:
clr2 = (0xFF, 0, 0) # Red
elif clr > 225:
clr2 = (0xA5, 0xA2, 0x2A) # Brown
elif clr > 210:
clr2 = (0xFF, 0x63, 0x47) # Tomato
elif clr > 195:
clr2 = (0xFA, 0x80, 0x72) # Salmon
elif clr > 180:
clr2 = (0x7B, 0x68, 0xEE) # MediumSlateBlue
elif clr > 165:
clr2 = (0xFF, 0xFF, 0) # Yellow
elif clr > 145:
clr2 = (0xFF, 0xEF, 0xD5) # PapayaWhip
elif clr > 125:
clr2 = (0xEE, 0x82, 0xEE) # Violet
elif clr > 105:
clr2 = (0xDB, 0x70, 0x93) # PaleVioletRed
elif clr > 90:
clr2 = (0x9A, 0xCD, 0x32) # YellowGreen
elif clr > 75:
clr2 = (0, 255, 0) # Green
elif clr > 60:
clr2 = (0, 0xFF, 0x7F) # SpringGreen
elif clr > 50:
clr2 = (0, 0xFA, 0x9A) # MediumSpringGreen
elif clr > 40:
clr2 = (0x3C, 0xB3, 0x71) # MediumSeaGreen
elif clr > 30:
clr2 = (0x46, 0x82, 0xB4) # SteelBlue
elif clr > 20:
clr2 = (0x41, 0x69, 0xE1) # RoyalBlue
elif clr > 10:
clr2 = (0, 0, 255) # Blue
else:
clr2 = (0, 0, 0xCD) # MediumBlue
vp2[j, i, :] = clr2
return vp2
else:
return np.rot90(vp)
def plot():
global vp
if gl:
if step == 1: vp = vp.flatten()
vp = (GLubyte * len(vp))(*vp)
window = Window(visible = True, width = w, height = w, caption = ('nH = ' + str(nH)))
@window.event
def on_draw():
window.clear()
glDrawPixels(w, w, GL_RGB, GL_UNSIGNED_BYTE, vp)
app.run()
else:
plt.figure(figsize = (3, 3))
plt.title('Нагревателей: ' + str(nH))
plt.imshow(vp, cmap = 'jet', interpolation = 'nearest') # origin = 'lower'
plt.axis('off')
plt.show()
if step == 1:
grid() # Инициализация сетки (области интегрирования)
s_t = time.time()
solve(vp) # Решаем краевую задачу
s_t2 = time.time()
print('Потрачено на решение:', round(s_t2 - s_t, 1))
vp = make_map(vp)
save_data(fn, vp)
if gl:
print('Потрачено на подготовку данных:', round(time.time() - s_t2, 1))
plot() # Вывод карты температур
elif step == 2:
if many_files:
from pyglet import clock
def callback(dt):
global vp, n_f
n_f += 1
if n_f > 10: n_f = 1
fn = fn0 + str(n_f) + '.bin'
vp = load_data(fn)
vp = (GLubyte * len(vp))(*vp)
clock.schedule_interval(callback, 1.5)
n_f = 1
fn = fn0 + str(n_f) + '.bin'
vp = load_data(fn)
plot() # Вывод карты температур
else:
vp = load_data(fn)
if not gl:
vp = vp.reshape(n2, n2)
plot() # Вывод карты температур
Полученная анимация может быть захвачена и сохранена в виде gif-файла, например, GifCam. Затем gif-файл можно конвертировать, например, в mp4-файл, применив, скажем, Movavi Video Suite.
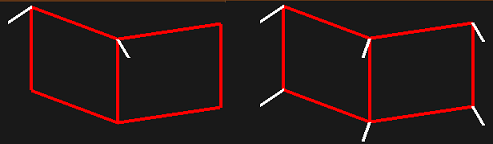
Наложение текстуры на грани призмы.


from pyglet.gl import *
import pyglet
from pyglet import app, graphics
from pyglet.window import Window, key
import numpy as np
d, d1, d2 = 5, 10, 15
wx, wy = 1.5 * d2, 1.5 * d2
width, height = int(30 * wx), int(30 * wy)
window = Window(visible = True, width = width, height = height, resizable = True)
glClearColor(0.1, 0.1, 0.1, 1.0)
glClear(GL_COLOR_BUFFER_BIT)
def texInit():
iWidth = iHeight = 64
n = 3 * iWidth * iHeight
img = np.zeros((3, iWidth, iHeight), dtype = 'uint8')
for i in range(iHeight):
for j in range(iWidth):
img[:, i, j] = ((i - 1) & 16 ^ (j - 1) & 16) * 255
img = img.reshape(n)
img = (GLubyte * n)(*img)
p, r = GL_TEXTURE_2D, GL_RGB
glTexParameterf(p, GL_TEXTURE_WRAP_S, GL_REPEAT)
glTexParameterf(p, GL_TEXTURE_WRAP_T, GL_REPEAT)
glTexParameterf(p, GL_TEXTURE_MAG_FILTER, GL_LINEAR)
glTexParameterf(p, GL_TEXTURE_MIN_FILTER, GL_LINEAR)
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE, GL_DECAL)
glTexImage2D(p, 0, r, iWidth, iHeight, 0, r, GL_UNSIGNED_BYTE, img)
glEnable(p)
texInit()
zv = -d2/2
v0, v1, v2, v3 = (-d2,d2,zv), (-d1,d1,0), (d1,d1,0), (d2,d2,zv)
@window.event
def on_draw():
window.clear()
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
glOrtho(-wx, wx, -wy, wy, -20, 20)
glRotatef(90, 1, 0, 0)
graphics.draw(4, GL_QUADS, ('v3f', (v0 + v1 + v2 + v3)), ('t2f', (0,1, 0,0, 1,0, 1,1)))
app.run()
Состоит из двух частей. В первой ведется работа с многослойным перцептроном, во второй – со сверточными слоями.
Требования к отчету:
Контрольные вопросы и задачи:
Состоит из двух частей. В первой создается и анализируется набор данных с зашумленных изображениями кривых и геометрических фигур, во второй – обучается НС, классифицирующая изображения созданного в первой части набора данных.
Отчет по задаче 224 включает:
Отчет по задаче 225 включает:
Выводится в зависимости от значения fun_no:
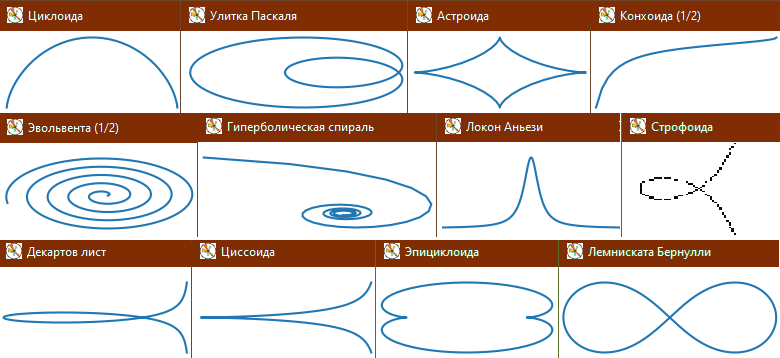
import matplotlib.pyplot as plt, math, numpy as np
from sys import exit
fun_no = 9 # 1, 2, 3, ..., 12
if fun_no < 1 or fun_no > 12: fun_no = 3
if fun_no == 1: # Циклоида
nm = 'Циклоида'
r = 15
t = np.linspace(0, 2 * np.pi, 50)
x = r * t - r * np.sin(t)
y = r - r * np.cos(t)
elif fun_no == 2: # Улитка Паскаля
nm = 'Улитка Паскаля'
r = 5
h = 17
t = np.linspace(0, 2 * np.pi, 500)
x = 2 * r * np.cos(t) - h * np.cos(2 * t)
y = 2 * r * np.sin(t) - h * np.sin(2 * t)
elif fun_no == 3: # Астроида
nm = 'Астроида'
a = 15
t = np.linspace(0, 2 * np.pi, 50)
x = a * np.cos(t)**3
y = a * np.sin(t)**3
elif fun_no == 4: # Конхоида (1/2)
nm = 'Конхоида (1/2)'
a = 15
b = 8
t = np.linspace(-0.95 * np.pi / 2, 0 * np.pi / 2, 50)
#t2 = np.linspace(1.05 * np.pi / 2, 0.95 * 3 * np.pi / 2, 50)
#t = np.concatenate((t, t2))
x = a + b * np.cos(t)
y = a * np.tan(t) + b * np.sin(t)
elif fun_no == 5: # Эвольвента (1/2)
nm = 'Эвольвента (1/2)'
r = 1
t = np.linspace(0, 30, 500)
x = r * (np.cos(t) + t * np.sin(t))
y = r * (np.sin(t) - t * np.cos(t))
elif fun_no == 6: # Гиперболическая спираль
nm = 'Гиперболическая спираль'
r = 1
t = np.linspace(-30, -1, 100)
#t2 = np.linspace(1, 30, 100)
#t = np.concatenate((t, t2))
x = r * np.cos(t) / t
y = r * np.sin(t) / t;
elif fun_no == 7: # Локон Аньези
nm = 'Локон Аньези'
a = 1
t = np.linspace(0.1, np.pi - 0.1, 100)
x = 2 * a / np.tan(t); y = 2 * a * np.sin(t)**2
elif fun_no == 8: # Декартов лист
nm = 'Декартов лист'
a = 10
t = np.linspace(-5, 5, 300)
x = a * (t**2 - 1) / (3 * t**2 + 1)
y = a * t * (t**2 - 1) / (3 * t**2 + 1)
elif fun_no == 9: # Циссоида
nm = 'Циссоида'
a = 10
t = np.linspace(-5, 5, 100)
x = 2 * a * t**2 / (t**2 + 1)
y = 2 * a * t**3 / (t**2 + 1)
elif fun_no == 10: # Строфоида
nm = 'Строфоида'
a = 25
t = np.linspace(-2, 2, 100)
x = a * (t**2 - 1) / (t**2 + 1)
y = a * t * (t**2 - 1) / (t**2 + 1)
x_min = int(min(x))
x_max = int(max(x))
y_min = int(min(y))
y_max = int(max(y))
# Нужно уместить в 64*64
dx = int((64 - (x_max - x_min)) / 2) # Половина свободного пространства по x
dy = int((64 - (y_max - y_min)) / 2) # Половина свободного пространства по y
shift_x = abs(x_min) + dx # Сдвиг по x
shift_y = abs(y_min) + dy # Сдвиг по y
w = h = 64 # Ширина и высота рисунка
arrPic = np.zeros((w, h), dtype = np.uint8)
clr_mim, clr_max = 75, 255 # Диапазон оттенков серого цвета
for x, y in zip(x, y):
ix = int(x) + shift_x
iy = int(y) + shift_y
clr = np.random.randint(clr_mim, clr_max)
arrPic[iy, ix] = clr
plt.figure(nm)
plt.imshow(arrPic, cmap = 'gray')
plt.axis('off')
plt.show()
exit()
elif fun_no == 11: # Эпициклоида
nm = 'Эпициклоида'
r = 5
t = np.linspace(0, 2 * np.pi, 100)
x = 3*r*np.cos(t) - r*np.cos(3*t)
y = 3*r*np.sin(t) - r*np.sin(3*t)
elif fun_no == 12: # Лемниската Бернулли
nm = 'Лемниската Бернулли'
a = 5
t = np.linspace(-70, 70, 5000)
x = a * np.sqrt(2) * (t + t**3) / (1 + t**4)
y = a * np.sqrt(2) * (t - t**3) / (1 + t**4)
plt.figure(nm)
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x, y)
plt.show()

Данные сохраняются в двоичные файлы.
import numpy as np
import math, time
import matplotlib.pyplot as plt
from PIL import Image # Для поворота изображения
#
np.random.seed(348)
full = not True # Полный прямоугольник, если True
cls = 0 if full else 1
show = True
show_test = False
fn_train = 'dataTrain.bin'
fn_train_labels = 'labelsTrain.bin'
fn_test = 'dataTest.bin'
fn_test_labels = 'labelsTest.bin'
n_train = 600 # Число рисунков для обучения
n_test = 100 # Число тестовых рисунков
clr_mim, clr_max = 75, 255 # Диапазон оттенков серого цвета
w, h = 64, 64 # Ширина и высота рисунка
w2 = w / 2
border = 4 # Граница
#
def line(arrPic, s, e, v, hor = True):
for i in range(s, e):
rnd = int(np.random.uniform(-2, 2))
if hor:
arrPic[v, i] = np.random.randint(100, 255)
arrPic[v + rnd, i] = np.random.randint(100, 255)
else:
arrPic[i, v] = np.random.randint(100, 255)
arrPic[i, v + rnd] = np.random.randint(100, 255)
def rect(arrPic):
xL = np.random.randint(6, 24)
xR = np.random.randint(40, 58)
yB = np.random.randint(6, 24)
yT = np.random.randint(40, 58)
if yT - yB == xR - xL:
yB -= 1
yT -= 1
xL -= 1
xR += 1
if full:
idx = range(4)
else:
mis = np.random.randint(4) # Номер отсутствующей стороны
idx = [i for i in range(4) if i != mis]
for i in idx:
if i == 0: line(arrPic, xL, xR, yB)
if i == 1: line(arrPic, xL, xR, yT)
if i == 2: line(arrPic, yB, yT, xL, False)
if i == 3: line(arrPic, yB, yT, xR, False)
#
def prepareData(n, fn, fn2):
file = open(fn, 'wb')
file2 = open(fn2, 'wb')
xs0 = border - w2 + 1
xe = w2 - border - 1
dx = 0.1
for i in range(n):
if full: # Прямоугольник
xs = xs0
label = cls
else: # Прямоугольник без одной стороны
xs = xs0
label = cls
arrPic = np.zeros((w, h), dtype = np.uint8)
rect(arrPic)
ang = np.random.randint(-90, 90)
arrPic = rot_img(ang, arrPic)
file.write(arrPic)
file2.write(np.uint8(label))
file.close()
file2.close()
#
def load_data(fn, fn2):
with open(fn, 'rb') as read_binary:
data = np.fromfile(read_binary, dtype = np.uint8)
with open(fn2, 'rb') as read_binary:
labels = np.fromfile(read_binary, dtype = np.uint8)
return data, labels
#
def rot_img(ang, img_array):
# Приводим данные к типу uint8
img_array = np.array(img_array, dtype = 'uint8')
# Формируем изображение по массиву img_array
img = Image.fromarray(img_array, 'L')
# Поворот изображения на угол ang против часовой стрелки
img = img.rotate(ang)
# Переводим изображение в массив
ix = img.size[0]
iy = img.size[1]
img_array_rot = np.array(img.getdata(), dtype = 'uint8').reshape(iy, ix)
return img_array_rot
if not show:
t0 = time.time()
print('Поехали')
prepareData(n_train, fn_train, fn_train_labels)
prepareData(n_test, fn_test, fn_test_labels)
print('Потрачено времени:', round(time.time() - t0, 3))
else:
def plotData(data, ttl):
plt.figure(ttl)
k = 0
for i in range(30):
j = np.random.randint(data.shape[0])
k += 1
plt.subplot(3, 10, k)
plt.imshow(data[i], cmap = 'gray')
plt.title(cls, fontsize = 11)
plt.axis('off')
plt.subplots_adjust(hspace = -0.1) # wspace
plt.show()
if show_test:
test_data, _ = load_data(fn_test, fn_test_labels)
data_show = test_data.reshape(n_test, w, h)
else:
train_data, _ = load_data(fn_train, fn_train_labels)
data_show = train_data.reshape(n_train, w, h)
ttl = 'Прямоугольник'
plotData(data_show, ttl)
Для поворота взамен PIL можно употребить следующий код (используются данные MNIST):
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from PIL import Image # Для поворота изображения
from skimage.measure import compare_ssim
def PIL_rot(img, ang):
# Формируем изображение по массиву img_array
img = Image.fromarray(img, 'L')
# Поворот изображения на угол ang против часовой стрелки
img = img.rotate(ang)
# Переводим изображение в массив
img = np.array(img)
return img
def show_x(img0, img1, img):
def sp(n, img, ttl):
plt.subplot(1, 3, n)
plt.title(ttl)
plt.axis('off')
plt.imshow(img, cmap = 'gray')
sp(1, img0, 'Исходное')
sp(2, img1, 'Программа')
sp(3, img, 'PIL')
plt.show()
def loadBinData(img_rows, img_cols):
print('Загрузка данных из двоичных файлов...')
with open('imagesTrain.bin', 'rb') as f:
x_trn = np.fromfile(f, dtype = np.uint8)
with open('imagesTest.bin', 'rb') as f:
x_tst = np.fromfile(f, dtype = np.uint8)
x = np.concatenate([x_trn, x_tst])
x = x.reshape(x.shape[0] // (img_rows * img_cols), img_rows, img_cols)
return x
def rot_img(img, ang):
def fill_in(vr, sy, sx, cs, sn, img, img_rot):
cy, cx = sy // 2, sx // 2
for j in range(sy):
for i in range(sx):
clr = img[i, j]
if clr == 0: continue
y0, x0 = i - cy, j - cx
y = x0 * sn + y0 * cs
x = x0 * cs - y0 * sn
ry = round(y)
rx = round(x)
if 0 <= cy + ry < sy and 0 <= cx + rx < sx:
if vr == 1:
new_i, new_j = cy + int(ry), cx + int(rx)
img_rot[new_i, new_j] = clr
else:
new_i, new_j = cy + int(y), cx + int(x)
if img_rot[new_i, new_j] == 0: img_rot[new_i, new_j] = clr
ang = -ang # Поворот против часовой стрелки
ang_radian = ang / 180 * np.pi
cs, sn = np.cos(ang_radian), np.sin(ang_radian)
img_rot = np.zeros(img.shape, dtype = 'uint8')
sy, sx = img.shape[0], img.shape[1]
fill_in(1, sy, sx, cs, sn, img, img_rot)
fill_in(2, sy, sx, cs, sn, img, img_rot)
return img_rot
img_rows = img_cols = 28
x = loadBinData(img_rows, img_cols)
ang = 30
ind = 2088 # np.random.randint(0, len(x) - 1)
img = x[ind]
img_rot = rot_img(img, ang) # Поворот изображения
pil_img = PIL_rot(img, ang)
print('Сходство программа vs PIL:', compare_ssim(img_rot / 255, pil_img / 255))
show_x(img, img_rot, pil_img)
# Поворот на -ang для сравнения с исходным изображением
img_rot = rot_img(img_rot, -ang)
pil_img = PIL_rot(pil_img, -ang)
print('Сходство исходное vs программа:', compare_ssim(img / 255, img_rot / 255))
print('Сходство исходное vs PIL:', compare_ssim(img / 255, pil_img / 255))
show_x(img, img_rot, pil_img)
# После поворота на 30
# Сходство программа vs PIL: 0.8753
# После поворота на -30
# Сходство исходное vs программа: 0.906
# Сходство исходное vs PIL: 0.9625
Результаты после поворота на 30° и обратного поворота на -30°.


Данные сохраняются в двоичные файлы.
import numpy as np
import math, time
import matplotlib.pyplot as plt
#
np.random.seed(348)
show = not True
show_test = False
fn_train = 'dataTrain.bin'
fn_train_labels = 'labelsTrain.bin'
fn_test = 'dataTest.bin'
fn_test_labels = 'labelsTest.bin'
n_train = 600 # Число рисунков для обучения
n_test = 100 # Число тестовых рисунков
clr_mim, clr_max = 75, 255 # Диапазон оттенков серого цвета
w, h = 64, 64 # Ширина и высота рисунка
w2 = w / 2
border = 1 # Граница
#
def parab(x, coef):
x_noise = np.random.uniform(-0.5, 0.5)
y_noise = np.random.uniform(-4, 4)
y = coef * (x + x_noise)**2 + border + 2 + y_noise
return y
#
def one_class(n, fn, fn2):
file = open(fn, 'wb')
file2 = open(fn2, 'wb')
xe = w2 - border - 1
dx = 0.1
xs = 0
label = 0
for i in range(n): # n - число примеров
sgn = np.random.randint(2) # x или -x
coef_noise = np.random.uniform(0.3, 3.0)
coef = 0.07 * coef_noise
arrPic = np.zeros((w, h), dtype = np.uint8)
x = xs - dx
while x < xe:
x += dx
y = parab(x, coef)
if sgn == 1:
ix = min(w - 1, int(w2 + x))
else:
ix = max(0, int(w2 - x))
iy = h - int(y)
iy = max(0, iy)
iy = min(h - 1, iy) # Уходим из физической системы координат
clr = np.random.randint(clr_mim, clr_max)
arrPic[iy, ix] = clr
file.write(arrPic)
file2.write(np.uint8(label))
file.close()
file2.close()
#
def load_data(fn, fn2):
with open(fn, 'rb') as read_binary:
data = np.fromfile(read_binary, dtype = np.uint8)
with open(fn2, 'rb') as read_binary:
labels = np.fromfile(read_binary, dtype = np.uint8)
return data, labels
#
if not show:
t0 = time.time()
print('Поехали')
one_class(n_train, fn_train, fn_train_labels)
one_class(n_test, fn_test, fn_test_labels)
print('Потрачено времени:', round(time.time() - t0, 3))
else:
def plotData(data, ttl, cls):
plt.figure(ttl)
k = 0
for i in range(30):
j = np.random.randint(data.shape[0])
k += 1
plt.subplot(3, 10, k)
plt.imshow(data[i], cmap = 'gray')
plt.title(cls, fontsize = 11)
plt.axis('off')
plt.subplots_adjust(hspace = -0.1) # wspace
plt.show()
if show_test:
test_data, _ = load_data(fn_test, fn_test_labels)
data_show = test_data.reshape(n_test, w, h)
else:
train_data, _ = load_data(fn_train, fn_train_labels)
data_show = train_data.reshape(n_train, w, h)
ttl = '1/2 параболы'
cls = 0
plotData(data_show, ttl, cls)
| № | ФИО | 2 | 8 | 15 | 18 | 19 | 22 | 25 | 200 | 203 | 224 | %И | %Д |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Алешина Софья | Д | 9 | 8 | И | 9 | 9 | 6 | Д | 8 | 6 | 85.0 | 85.0 |
| 2 | Аршинова Диана | Д | 9 | 7 | И | 8 | 7 | 6 | 8 | 9 | 9 | 78.3 | 90.0 |
| 3 | Волков Евгений | - | - | - | - | - | - | - | - | - | - | 0.0 | 0.0 |
| 4 | Гаврилова Дарья | Д | И | 8 | И | И | 8 | 8 | Д | Д | 7 | 90.0 | 92.5 |
Вариант 1.
Вариант 2.
Значение size берется из следующего списка.
Подготовка к ЛР 11.
Программа 1.
Программа 2.
Пример:
# wv – индексированные векторы слов
wv = wv_model.wv
# Словарь модели
vocab = wv.vocab # class 'dict'
sen = 'чтоб не упасть дорогой склизкой'
print(sen)
sen = sen.split()
for w in sen:
if vocab.get(w) is None:
print('Слова', w, 'нет в словаре')
pred_words = wv_model.predict_output_word([sen[0], sen[1], sen[3], sen[4]], topn = 5)
print(pred_words)
Результат:
чтоб не упасть дорогой склизкой
Слова склизкой нет в словаре
[('упасть', 0.0121), ('такого', 0.0096), ('хочу', 0.0087), ('тайны', 0.0078), ('того', 0.0059)]
Метрики:
from scipy.spatial import distance
from skimage.measure import compare_ssim
dist = distance.euclidean(im1, im2) # Евклидово расстояние
dist_cs = distance.cosine(im1, im2) # Косинусное расстояние
sim = compare_ssim(im1, im2) # Индекс структурного сходства изображений
где im1, im2 – векторы, содержащие данные об изображениях.
В случае compare_ssim расстояние оценивается как 1 – sim.
Случайное целое число от 0 до N-1:
k = np.random.randint(N)
Сортировка списка по ключу:
x = [['c', 8], ['b', 5], ['a', 3]]
x.sort(key = lambda r:(r[1]))
# [['a', 3], ['b', 5], ['c', 8]]
Результат:
Результат представляется в виде отчета, содержащего:
- задание;
- алгоритм;
- входные данные;
- выходные данные;
- программу.
Набор данных: MNIST.
1. Написать процедуру, определяющую вертикальный сдвиг изображения цифры.
Вертикальный сдвиг равен нулю, если изображение центрировано по оси Y.
Используя эту процедуру, найти и вывести изображения с максимальным и минимальным вертикальным сдвигом в обучающем и проверочном множествах.
2. Задать цифру.
Найти поочередно в обучающем и проверочном множествах два наиболее похожих изображения, используя поочередно следующие метрики:
- евклидово расстояние;
– косинусное расстояние;
- индекс структурного сходства.
Вывести расстояние, индексы и рисунки цифр.
Замерить время поиска изображений.
3. Задать вид множества (обучающее или проверочное).
Выбрать в заданном множестве случайным образом изображение и найти наиболее похожее на него изображение, используя поочередно следующие метрики:
- евклидово расстояние;
– косинусное расстояние;
- индекс структурного сходства.
Вывести для каждого множества расстояние, индексы и рисунки выбранного и найденного изображений.
4. Задать цифру и вид множества (обучающее или проверочное).
Найти n (n >= 2) изображений, наиболее близких к обобщенному образу цифры, используя поочередно следующие метрики:
- евклидово расстояние;
– косинусное расстояние;
- индекс структурного сходства.
Вывести найденное расстояние, индексы и рисунки найденных изображений.
5. Задать цифру и вид множества (обучающее или проверочное).
Найти центральное изображение и n (n >= 2) изображений, наиболее удаленных от центрального изображения.
Центральное изображение - это изображение, наиболее близкое к обобщенному изображению.
Вывести найденные расстояния, индексы и рисунки найденных изображений.
Метрика - любая.
6. Задать цифру и вид множества (обучающее или проверочное).
Найти граничные изображения и затем изображение с наименьшим суммарным расстоянием до граничных изображений.
Граничные изображения - два наиболее удаленных изображения.
Вывести индексы и рисунки найденных изображений.
Метрика - любая.
7. Задать вид множества (обучающее или проверочное).
Среди подмножеств изображений указать подмножество с наименьшим минимальным расстоянием между его изображениями.
Подмножество изображений - это совокупность изображений с одинаковой меткой.
Вывести список с элементами [метка, минимальное расстояние], упорядоченный по последнему показателю
и n (n >= 10) примеров рисунков случайно выбранных изображений из найденного подмножества.
8. Выполнить, используя ImageDataGenerator, генерацию данных на основе обучающего и проверочного множеств.
Сформировать множество пар изображений-аналогов. (Берутся изображения одинаковых цифр).
Изображения А и Б являются аналогами, если индекс структурного сходства этих изображений более sim_a (sim_a > 0.7).
Изображение А берется из обучающего множества, а Б - из тестового.
Вывести 20 пар изображений сформированного множества (или все, если его размер менее 20).
Вывести размер найденного множества, а также список с элементами [цифра, число аналогов],
отсортированный по числу аналогов.
Метрика - индекс структурного сходства.
9. Задать вид множества (обучающее или проверочное).
Внести шум в n (n >= 10) случайно выбранных изображений,
изменив случайным образом значения не менее 15% нулевых пикселей в каждом из них.
Изменяемый пиксель так же выбирается случайно.
Вывести метки, индексы и рисунки изображений до и после изменения.
10. Задать вид множества (обучающее или проверочное).
Найти последовательно в обучающем и проверочном множествах два самых похожих изображения цифр 1 и 7,
используя поочередно следующие метрики:
- евклидово расстояние;
– косинусное расстояние;
- индекс структурного сходства.
Вывести расстояние, индексы и рисунки найденных изображений.
Для сокращения объема вычислений использовать подвыборки из сформированных множеств.
11. Выполнить, используя ImageDataGenerator, генерацию данных на основе обучающего и проверочного множеств.
Найти два самых похожих изображения каждой из цифр (0, 1, ..., 9), выбирая первое из множества, полученного на основе обучающего,
а второе - на основе проверочного.
Вывести индексы и рисунки найденных изображений.
Метрика любая.
Для сокращения объема вычислений использовать подвыборки из сформированных множеств.
12. Задать вид множества (обучающее или проверочное).
Упорядочить множество по числу пустых пикселей в изображении (в убывающем порядке).
Вывести рисунки цифр упорядоченного множества с шагом 100
и отдельно рисунки первого, последнего и разности последнего и первого изображений упорядоченного множества.
13. Найти и вывести в обучающем и проверочном множествах изображения
с максимальным и минимальным горизонтальным сдвигом.
Горизонтальный сдвиг равен нулю, если изображение центрировано по оси X.
14. Задать вид множества (обучающее или проверочное).
А. Выполнить, используя ImageDataGenerator, генерацию данных на основе выбранного множества.
Б. Вычислить расстояние между обобщенными портретами исходных и сгенерированных данных.
В. Запомнить обобщенные портреты исходных и сгенерированных данных и полученное расстояние.
Повторить пункты А-В n раз (n >= 2).
Вывести полученные расстояния, рисунки обобщенных портретов и их разности.
15. Выполнить, используя ImageDataGenerator, генерацию данных на основе обучающего и проверочного множеств.
Найти для каждой из цифр в каждом из сгенерированном множестве максимально разделенные изображения.
Вывести найденные расстояние и изображения (рисунки).
Метрика любая.
Для сокращения объема вычислений использовать подвыборки из сформированных множеств.
16. Выполнить, используя ImageDataGenerator, генерацию данных на основе обучающего и проверочного множеств.
Определить, оперируя подвыборками из полученных множеств, DAi - средние расстояния между изображениями одинаковых цифр
(первое изображение берется из множества, полученного на основе обучающего, а второе - на основе проверочного).
Вывести список вида [i, DAi], упорядоченный по DAi (i = 0, 1, ..., 9).
Взять первую цифру этого списка и вывести два изображения, расстояние между которыми наиболее близко к DAi
(одно изображение берется из множества, полученного на основе обучающего, а второе - на основе проверочного).
Вывести расстояние между выведенными изображениями.
Метрика любая.
17. Сформировать список минимальных расстояний между изображениями обучающего и проверочного множеств одинаковых цифр.
Для каждой цифры сформировать множество пар изображений, расстояние между которыми больше соответствующего минимального расстояния,
не более чем на P%. (Значение P случайным образом берется из отрезка [5, 10]).
Вывести список вида [цифра, число пар изображений, отвечающих критерию P], упорядоченный по второму показателю.
Вывести 20 пар изображений сформированного множества (или все, если его размер менее 20).
В противном случае вывести 20 случайно выбранных пар изображений сформированного множества.
Метрика любая.
18. Задать цифру.
Найти в обучающем и проверочном множествах изображения с максимальным и минимальным числом загруженных пикселей (то есть пикселей с ненулевым значением цвета).
Вывести найденные максимальные и минимальные значения, индексы и найденные изображения (рисунки).
19. Создать процедура поворота изображения. Используя эту процедуру, выполнить поворот случайно выбранной цифры на заданный угол.
Сравнить, используя индекс структурного сходства, результат с изображением, полученным в результате поворота той же цифры с помощью метода rotate библиотеки PIL.
import numpy as np
import matplotlib.pyplot as plt
from PIL import Image # Для поворота изображения
def img_rot(img, ang):
# Формируем изображение по массиву img (тип данных – 'uint8')
img = Image.fromarray(img, 'L')
# Поворот изображения на угол ang против часовой стрелки
img = img.rotate(ang)
# Переводим изображение в массив
ix = img.size[0]
iy = img.size[1]
img = np.array(img.getdata()).reshape(iy, ix)
return img
... Получаем изображение img - массив формы (28, 28)
ang = 30
img = img_rot(img, ang) # Поворот изображения
Вариант 1. Написать процедуру вывода отрезка прямой с интерполяцией цветов. При выводе отрезка использовать алгоритм Брезенхема.
Вывести, используя созданную процедуру, четырехугольник и его диагонали.
Координаты вершин фигуры случайным образом берутся из следующих интервалов:
x0, y0: [2, 11], [2, 11]
x1, y1: [39, 48], [2, 11]
x2, y2: [39, 48], [39, 48]
x3, y3: [2, 11], [39, 48]
Цвет в вершинах:
clr0: [255, 0, 0]
clr1: [0, 255, 0]
clr2: [0, 0, 255]
clr3: [255, 255, 0]
Заданный цвет выводится в углах области вывода.
Пример.
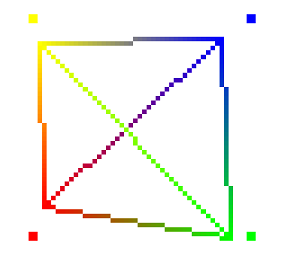
Вариант 2. Написать процедуру отсечения на основе алгоритма разбиения средней точкой.
Используя созданную процедуру, выполнить отсечение в области
(XL, YB) = (9, 11), (XR, YT) = (39, 29)
следующих отрезков:
Отрезок 1:
(x1, y1) = (2, 4), (x11, y11) = (48, 32)
Отрезок 2:
(x2, y2) = (48, 8), (x22, y22) = (20, 22)
Отрезок 3:
(x3, y3) = (13, 25), (x33, y33) = (35, 27)
Отрезок 4:
(x4, y4) = (2, 25), (x44, y44) = (13, 36)
Отрезок 5:
(x5, y5) = (13, 7), (x55, y55) = (37, 1)
При выводе отрезков использовать алгоритм Брезенхема.
Вывести начальную и конечную сцены:
Пример.
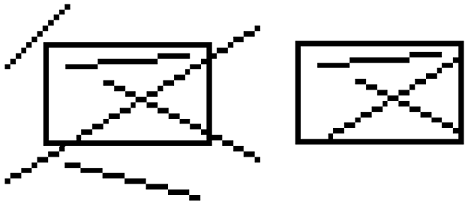
Вариант 3. Написать процедуру вывода отрезка прямой. При выводе отрезка использовать алгоритм Брезенхема.
Соединить, используя созданную процедуру, 6 случайно заданных точек.
Вдобавок вывести точки, используя следующие цвета:
[255, 0, 0]
[0, 255, 0]
[0, 0, 255]
[255, 255, 0]
[255, 0, 255]
[0, 255, 255]
Координаты точек выбираются из следующих интервалов:
x0, y0: [2, 60], [2, 10]
x1, y1: [2, 60], [12, 20]
x2, y2: [2, 60], [22, 30]
x3, y3: [2, 60], [32, 40]
x4, y4: [2, 60], [42, 50]
x5, y5: [2, 60], [52, 60]
Пример.
Вариант 4. Написать процедуру вывода отрезка прямой. При выводе отрезка использовать алгоритм Брезенхема.
Соединить, используя созданную процедуру, 6 случайно заданных точек, а затем конечную точку с начальной.
Вдобавок вывести точки, используя следующие цвета:
[255, 0, 0] – начальная точка;
[0, 255, 0];
[0, 0, 255];
[255, 255, 0];
[255, 0, 255];
[0, 255, 255] – конечная точка.
Координаты точек случайным образом выбираются из следующих интервалов:
x0, y0: [2, 10], [2, 60];
x1, y1: [12, 20], [2, 60];
x2, y2: [22, 30], [2, 60];
x3, y3: [32, 40], [2, 60];
x4, y4: [42, 50], [2, 60];
x5, y5: [52, 60], [2, 60].
При выводе отрезков использовать следующие цвета:
clr0 = [0, 0, 255] – первый отрезок, соединяющий (x0, y0) и (x1, y1);
clr1 = [255, 255, 0];
clr2 = [255, 0, 255];
clr3 = [0, 255, 255];
clr4 = [255, 0, 0];
clr5 = [0, 255, 0] – последний отрезок, соединяющий (x5, y5) и (x0, y0).
Пример.
1. OpenGL: преобразование координат. [Электронный ресурс] URL: http://100byte.ru/100btwrks/prjctn/prjctn.html. (Дата обращения: 01.09.2020).
2. Вывод граней OpenGL. [Электронный ресурс] URL: http://100byte.ru/stdntswrks/gl/gl.html. (Дата обращения: 01.09.2020).
3. C#, OpenGL: вывод стандартных примитивов. [Электронный ресурс] URL: http://100byte.ru/stdntswrks/cshrp/stdprmtvs/stdprmtvs.html. (Дата обращения: 01.09.2020).
4. Построение, текстурирование и тонирование сферы. [Электронный ресурс] URL: http://100byte.ru/stdntswrks/cshrp/sphTK/sphTK.html. (Дата обращения: 01.09.2020).
5. Шейдер с иллюзией выступов и впадин. [Электронный ресурс] URL: http://100byte.ru/stdntswrks/cshrp/mapTK/mapTK.html. (Дата обращения: 01.09.2020).
6. Шейдер с картой-кубом в задаче воспроизведения глобуса.Шейдер с картой-кубом в задаче воспроизведения глобуса. [Электронный ресурс] URL: http://100byte.ru/stdntswrks/cshrp/earthCubeMapTK/earthCubeMapTK.html. (Дата обращения: 01.09.2020).
7. Шейдерная реализация освещения по Блинну и Фонгу. [Электронный ресурс] URL: http://100byte.ru/stdntswrks/cshrp/blinnPhongPart/blinnPhong.html. (Дата обращения: 01.09.2020).
8. Вывод текста.. [Электронный ресурс] URL: http://100byte.ru/stdntswrks/cshrp/txt.html. (Дата обращения: 01.09.2020).
9. Вывод частиц. [Электронный ресурс] URL: http://100byte.ru/stdntswrks/cshrp/pf.html. (Дата обращения: 01.09.2020).
10. Руководство по программированию. [Электронный ресурс] URL: https://pyglet.readthedocs.io/en/latest/programming_guide/graphics.html. (Дата обращения: 01.09.2020).