Рассматривается нагрев прямоугольной пластины расположенными на ней источниками тепла. Температура источников тепла (нагревателей) не меняется во времени.
Определение стационарного распределения температуры в прямоугольной пластине сводится к следующей краевой задаче:

Ее запись в виде разностной схемы:
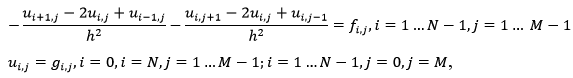
где
f = 0 во всех точках сетки, кроме позиций расположения источников тепла, в этих позициях f содержит значение температуры источника тепла,
g – содержит значения температуры на границах пластины.
В решаемой задаче полагаем:
пластина квадратная (M = N);
во всех граничных точках сетки, расположенных по периметру пластины, температура одинакова.
Задача решается методом сопряженных градиентов.
Пусть ui,j(0) - начальное приближение, тогда начальное значение невязки равно:
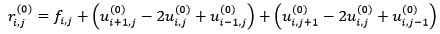
Запомним невязку:
pi,j(0) = ri,j(0)
Приближение и невязка на шаге k + 1 вычисляются по следующим формулам:
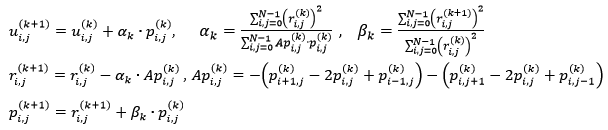
Вычисления завершаются при достижении заданной точности, определяемой как расстояние между последним и предшествующим приближениями.
На рис. 1 показаны результаты решения задачи с различным числом нагревателей.
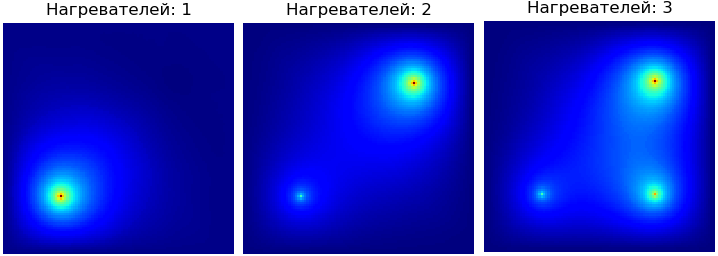
Рис. 1. Пластина с одним, двумя и тремя нагревателями
Замечание. Для согласования температурных карт с различным числом нагревателей необходимо выполнить нормирование данных по температуре.
Результаты обеспечивает следующий код:
import numpy as np
from matplotlib import pyplot as plt
nH = 3 # Число нагревателей (не более трех)
calc = True
g = 4 # Температура на границе
n = 100 # Размер сетки
n1 = n + 1
n2 = n + 2
eps = 0.5 # Точность: eps = pow(10, -2)
tH, tH2, tH3 = 60, 140, 100 # Температуры нагревателей 1, 2 и 3
# Координаты нагревателей 1, 2 и 3
xH, yH = n / 4, n / 4
xH2, yH2 = 3 * n / 4, 3 * n / 4
xH3, yH3 = xH2, yH
u = np.zeros((n2, n2), dtype = 'float32')
u_prev = np.zeros((n2, n2), dtype = 'float32')
max_steps = 100
fn = 'vp' + str(nH) + '.bin'
def save_data(fn, data):
fp = open(fn, 'wb')
fp.write(data.flatten())
fp.close()
def load_data(fn):
with open(fn, 'rb') as f:
data = np.fromfile(f, dtype = np.uint8)
return data
def f_r(x, y): # Правая часть
prs = 0.1
if abs(x - xH) < prs and abs(y - yH) < prs: return tH
if abs(x - xH2) < prs and abs(y - yH2) < prs and nH > 1: return tH2
if abs(x – xH3) < prs and abs(y – yH3) < prs and nH > 2: return tH3
return 0
def maxSumAMinusB(a, b):
max_val = -np.inf
for i in range(1, n1):
max_val = max(max_val, np.sum(abs(a[i, 1:n1] - b[i, 1:n1])))
return max_val
def sumAMultB(a, b):
return np.sum(a[1:n1, 1:n1] * b[1:n1, 1:n1])
def grid():
u[:, 0] = g; u[:, n1] = g
u[0, :] = g; u[n1, :] = g
def solve():
r = np.zeros((n1, n1), dtype = 'float32')
r_prev = np.zeros((n1, n1), dtype = 'float32')
ap = np.zeros((n1, n1), dtype = 'float32')
p = np.zeros((n2, n2), dtype = 'float32')
for i in range(1, n1):
for j in range(1, n1):
# Начальные невязки
up_ij2 = 2 * u[i, j]
r[i, j] = f_r(i, j) + (u[i + 1, j] - up_ij2 + u[i - 1, j]) + (u[i, j + 1] - up_ij2 + u[i, j - 1])
p[i, j] = r[i, j]
n_steps = m_val = 0
while(1):
for i in range(1, n1):
for j in range(1, n1):
u_prev[i, j] = u[i, j]
up_ij2 = 2 * p[i, j]
ap[i, j] = -(p[i + 1, j] - up_ij2 + p[i - 1, j]) - (p[i, j + 1] - up_ij2 + p[i, j - 1])
alpha = sumAMultB(r, r) / sumAMultB(ap, p)
u[1:n1, 1:n1] = u[1:n1, 1:n1] + alpha * p[1:n1, 1:n1] # Приближения
r_prev[1:, 1:] = r[1:, 1:]
r[1:, 1:] = r[1:, 1:] - alpha * ap[1:, 1:] # Невязки
betta = sumAMultB(r, r) / sumAMultB(r_prev, r_prev)
p[1:n1, 1:n1] = r[1:, 1:] + betta * p[1:n1, 1:n1]
# Сравнение текущего и предшествующего приближений на предмет достижения заданной точности
m_val = maxSumAMinusB(u, u_prev)
n_steps += 1
if m_val < eps or n_steps >= max_steps: break
print('Число шагов. Предельное:', max_steps, 'Сделано:', n_steps, 'Достигнутая точность:', m_val)
def make_map():
uMax = np.max(u)
vp = np.zeros((n2, n2), dtype = 'uint8')
vp[...] = 255 * u / uMax
return np.rot90(vp)
def plot():
plt.figure(figsize = (3, 3))
plt.title('Нагревателей: ' + str(nH))
plt.imshow(vp, cmap = 'jet', interpolation = 'nearest') # origin = 'lower'
plt.axis('off')
plt.show()
if calc:
grid() # Инициализация сетки (области интегрирования)
solve() # Решаем краевую задачу
vp = make_map()
save_data(fn, vp)
else:
vp = load_data(fn)
vp = vp.reshape(n2, n2)
plot() # Вывод карты температур
Приведенная схема так же реализуется как C# Windows Form-приложение. Графическое отображение результата (рис. 2) осуществляется встроенными в Microsoft Visual Studio средствами.
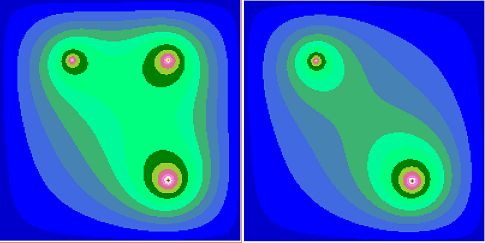
Рис. 2. Пластина с тремя и двумя нагревателями
Результат обеспечивает следующий код:
using System;
using System.Drawing;
using System.Windows.Forms;
namespace WindowsFormsApplicationTemprature
{
public partial class FormPlate : Form
{
// Граничное значение
int nH = 2; // Число нагревателей (не более трех)
int g = 4; // Температура на границе
static int N = 200; // Размер сетки
int N1 = N + 1;
int N2 = N + 2;
// Приближения текущего и предыдущего шагов
double[][] U, UPrev;
double eps; // Точность
int pW; // Размер области вывода
int penS; // Размер кисти
// Координаты нагревателей 1, 2 и 3
int xH, yH, xH2, yH2, xH3, yH3;
// Температуры нагревателей 1, 2 и 3
double tH = 80, tH2 = 120, tH3 = 100;
public FormPlate()
{
InitializeComponent();
eps = Math.Pow(10, -2);
pW = pictureBoxPlate.Width;
// Координаты нагревателей 1 и 2 (N <= pW)
int d = pW / N;
xH = 120 / d;
yH = 100 / d;
xH2 = 280 / d;
yH2 = 300 / d;
xH3 = xH2;
yH3 = yH;
// Размер кисти
penS = d;
// Инициализация сетки (области интегрирования)
Grid();
// Решаем краевую задачу
Solve();
// Вывод изображения
pictureBoxPlate.Paint += pictureBoxPlate_Paint;
}
double maxSumAMinusB(double[][] A, double[][] B)
{
double max = 0;
double sum;
for (int i = 1; i < N1; i++)
{
sum = 0;
for (int j = 1; j < N1; j++) sum += Math.Abs(A[i][j] - B[i][j]);
max = Math.Max(max, sum);
}
return max;
}
double sumAMultB(double[][] A, double[][] B)
{
double sum = 0;
for (int i = 1; i < N1; i++)
for (int j = 1; j < N1; j++) sum += (A[i][j] * B[i][j]);
return sum;
}
void Grid()
{
int i, j;
U = new double[N2][];
UPrev = new double[N2][];
for (i = 0; i < N2; i++)
{
U[i] = new double[N2];
UPrev[i] = new double[N2];
for (j = 0; j < N2; j++) U[i][j] = 0;
}
// Граница сетки (области интегрирования)
for (i = 0; i < N2; i++)
{
U[i][N1] = g;
U[i][0] = g;
j = i;
U[0][j] = g;
U[N1][j] = g;
}
}
// Правая часть
double f(int x, int y)
{
if (x == xH && y == yH) return tH;
if (x == xH2 && y == yH2 && nH > 1) return tH2;
if (x == xH3 && y == yH3 && nH > 2) return tH3;
return 0;
}
void Solve()
{
double[][] R = new double[N2][];
double[][] Rprev = new double[N2][];
double[][] P = new double[N2][];
double[][] AP = new double[N2][];
double alpha, betta, UPij2;
int i, j;
P[0] = new double[N2];
P[N1] = new double[N2];
for (i = 1; i < N1; i++)
{
R[i] = new double[N1];
Rprev[i] = new double[N1];
AP[i] = new double[N1];
P[i] = new double[N2];
}
// Граничные ячейки
for (i = 0; i < N2; i++)
{
P[i][0] = 0;
P[i][N1] = 0;
j = i;
P[0][j] = 0;
P[N1][j] = 0;
}
for (i = 1; i < N1; i++)
for (j = 1; j < N1; j++)
{
// Начальные невязки
UPij2 = 2 * U[i][j];
R[i][j] = f(i, j) + (U[i + 1][j] - UPij2 + U[i - 1][j]) + (U[i][j + 1] - UPij2 + U[i][j - 1]);
P[i][j] = R[i][j];
AP[i][j] = 0;
}
do
{
for (i = 1; i < N1; i++)
for (j = 1; j < N1; j++)
{
UPrev[i][j] = U[i][j];
UPij2 = 2 * P[i][j];
AP[i][j] = -(P[i + 1][j] - UPij2 + P[i - 1][j]) - (P[i][j + 1] - UPij2 + P[i][j - 1]);
}
alpha = sumAMultB(R, R) / sumAMultB(AP, P);
for (i = 1; i < N1; i++)
for (j = 1; j < N1; j++)
{
// Приближения
U[i][j] += alpha * P[i][j];
Rprev[i][j] = R[i][j];
// Невязки
R[i][j] -= alpha * AP[i][j];
}
betta = sumAMultB(R, R) / sumAMultB(Rprev, Rprev);
for (i = 1; i < N1; i++)
for (j = 1; j < N1; j++) P[i][j] = R[i][j] + betta * P[i][j];
}
// Сравнение текущего и предшествующего приближений на предмет достижения заданной точности
while (maxSumAMinusB(U, UPrev) >= eps);
}
// Вывод образа
void pictureBoxPlate_Paint(object sender, PaintEventArgs e)
{
int i, j;
Graphics plate = e.Graphics;
Pen penC;
double uMax = 0;
int clr;
Color clrC;
for (i = 0; i < N2; i++)
for (j = 0; j < N + 2; j++) uMax = Math.Max(uMax, U[i][j]);
for (i = 0; i < N2; i++)
for (j = 0; j < N + 2; j++)
{
clr = (int)(255 * U[i][j] / uMax);
if (clr > 240)
clrC = Color.Red; // FF000
else if (clr > 225)
clrC = Color.Brown; // A5A22A
else if (clr > 210)
clrC = Color.Tomato; // FF6347
else if (clr > 195)
clrC = Color.Salmon; // FA8072
else if (clr > 180)
clrC = Color.MediumSlateBlue; // 7B68EE
else if (clr > 165)
clrC = Color.Yellow; // FFFF00
else if (clr > 145)
clrC = Color.PapayaWhip; // FFEFD5
else if (clr > 125)
clrC = Color.Violet; // EE82EE
else if (clr > 105)
clrC = Color.PaleVioletRed; // DB7093
else if (clr > 90)
clrC = Color.YellowGreen; // 9ACD32
else if (clr > 75)
clrC = Color.Green; // 00FF00
else if (clr > 60)
clrC = Color.SpringGreen; // 00FF7F
else if (clr > 50)
clrC = Color.MediumSpringGreen; // 00FA9A
else if (clr > 40)
clrC = Color.MediumSeaGreen; // 3CB371
else if (clr > 30)
clrC = Color.SteelBlue; // 4682B4
else if (clr > 20)
clrC = Color.RoyalBlue; // 4169E1
else if (clr > 10)
clrC = Color.Blue; // 0000FF
else
clrC = Color.MediumBlue; // 0000CD
penC = new Pen(clrC, penS);
plate.DrawRectangle(penC, i * penS, j * penS, penS, penS);
}
}
}
}