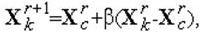 .
.
Тестирование метода Хука-Дживса на функции Розенброка показало его чувствительность к выбору начальной точки поиска экстремума функции.
В этой работе, опять же на функции Розенброка, реализуется и тестируется метод Нелдера-Мида [1].
Используются Фортран-, C#- и Python-реализации поиска минимума функции методом Нелдера-Мида.
В случае Фортран и C# метод Нелдера-Мида программируется, в случае Python используется метод minimize класса scipy.optimize библиотеки SciPy [2].
Замечание. Для поиска максимума нужно умножить на -1 результат, получаемый при вычислении значения оптимизируемой функции.
Алгоритмы формирования и преообразования симплекса иллюстрируются на Фортране [3]
В качестве тестовой берется функция Розенброка:
f(x1, x2) = (1 – x1)2 + 100 * (x2 – x12)2
Ее запись на Фортране:
real(8) function Rosenbrock(X, n)
real(8) X(n)
Rosenbrock = (1.0_8 - X(1))**2 + 100.0_8 * (X(2) - X(1) * X(1) )**2
end function Rosenbrock
Глобальный минимум функции равен 0.0 и находится в точке (x1, x2) = (1.0, 1.0).
При работе с функцией Розенброка для проверки используемого метода в качестве начальной часто берут точку
(-5, 10)
или точку
(-2.048, 2.048).
Приводимые программы могут работать с произвольной оптимизируемой функцией.
В начале работы алгоритма Нелдера-Мида строится регулярный симплекс: в пространстве Rn - это правильный многогранник, образованный n + 1 равноотстоящими друг от друга вершинами. Так, в R2 – это равносторонний треугольник. В пространстве Rn координаты вершин регулярного симплекса, в котором первая вершина
X = (x1, x2, ..., xn),
можно задать следующей матрицей:
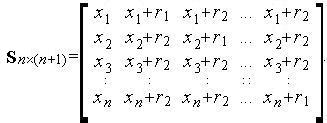
в которой в столбце i находятся координаты i-й вершины симплекса и
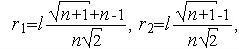
где l - длина ребра симплекса.
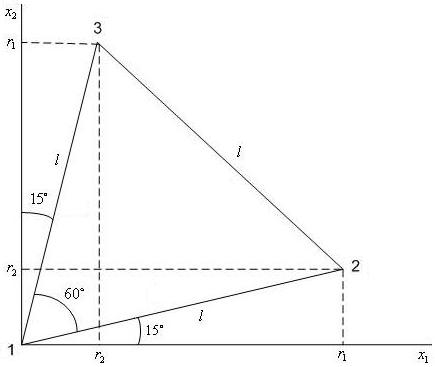
Так, в R2 из вершины X = (0, 0) регулярный симплекс (рис. 1) задается следующей матрицей:
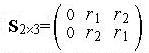 .
. .
.
Рис. 1. R2-регулярный симплекс из вершины X = (0, 0)
Построение регулярного симплекса выполняет следующая подпрограмма:
! Создает из точки X регулярный симплекс с длиной ребра L и с n + 1 вершиной
! Формирует массив FN значений оптимизируемой функции F в вершинах симплекса
subroutine makeSimplex(X, L, n)
real(8) X(:), L
integer n
real(8) qn, q2, r1, r2
qn = sqrt(1.0_8 + n) - 1.0_8
q2 = L / sqrt(2.0_8) * n
r1 = q2 * (qn + n)
r2 = q2 * qn
simplex(:, 1) = X
do i = 2, n + 1
simplex(:, i) = X + r2
end do
do i = 2, n + 1
simplex(i - 1, i) = simplex(i - 1, i) - r2 + r1
end do
do i = 1, n + 1
! Значения функции в вершинах симплекса
FN(i) = F(simplex(:, i), n)
end do
end subroutine makeSimplex
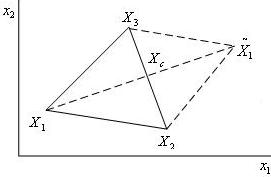
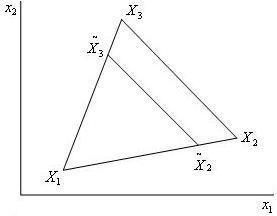
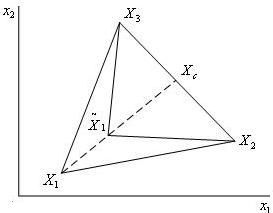
В алгоритме Нелдера-Мида используются следующие симплекс-операции:
 .
.
Рис. 2. Отражение R2-симплекса
 .
.
Рис. 3. Редукция R2-симплекса
 .
.
Рис. 4. Сжатие R2-симплекса
 .
.
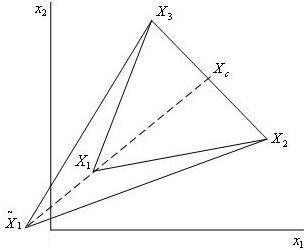
Рис. 5. Растяжение R2-симплекса
В процессе работы алгоритма после операции сжатия или растяжения симплекс преобразуется из регулярного в обычный.
Отражение вершины выполняется относительно Xc центра тяжести симплекса:
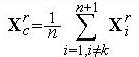 .
.
где k - номер отражаемой вершины, r - номер текущего шага алгоритма.
Координаты отраженной вершины вычисляются по следующей формуле:
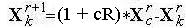 .
.
Обычно cR = 1.0. Координаты прочих вершин симплекса при выполнении операции отражения не меняются.
Центр тяжести симплекса возвращается следующей функцией:
function center_of_gravity(simplex, k, n)
real(8) center_of_gravity(n)
real(8), intent(in) :: simplex(n, n + 1)
integer, intent(in) :: k, n
integer j
do j = 1, n
center_of_gravity(j) = sum(simplex(j, :))
end do
center_of_gravity = (center_of_gravity - simplex(:, k)) / n
end function center_of_gravity
Отражение вершины с номером k относительно центра тяжести симплекса обеспечивает следующая подпрограмма:
subroutine reflection(simplex, k, cR, n)
real(8) simplex(n, n + 1)
! cR – коэффициент отражения
real(8), intent(in) :: cR
integer, intent(in) :: k, n
simplex(:, k) = (1 +cR) * center_of_gravity(simplex, k, n) - simplex(:, k)
end subroutine reflection
Редукция симплекса, – уменьшение длины всех ребер симплекса, выполняется к выбранной в алгоритме вершине Xk симплекса. Новые координаты редуцированного симплекса определяются по следующей формуле:
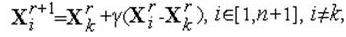 .
.
где γ - коэффициент редукции (положительное число, меньшее 1.0; часто берется значение 0.5), r - номер текущего шага алгоритма.
За редукцию симплекса отвечает следующая подпрограмма:
subroutine reduction(simplex, k, gamma, n)
real(8) simplex(n, n + 1)
real(8), intent(in) :: gamma
integer, intent(in) :: k, n
real(8) xk(n)
integer j
xk = simplex(:, k)
do j = 1, n
simplex(:, j) = xk + gamma * (simplex(:, j) - xk)
end do
simplex(:, k) = xk
end subroutine reduction
Сжатие симплекса выполняется в направлении Xk - Xc, где Xk - выбранная в алгоритме вершина симплекса, а Xc - центр его тяжести. В результате сжатия изменяются координаты вершины Xk:
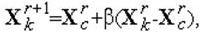 .
.
где β - коэффициент сжатия (положительное число, меньшее 1.0; нередко берется значение 0.5), r - номер текущего шага алгоритма.
Координаты прочих вершин симплекса не изменяются.
Растяжение симплекса выполняется в направлении Xk - Xc, где Xk - выбранная в алгоритме вершина, а Xc - центр его тяжести. В результате растяжения изменяются координаты вершины Xk:
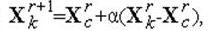 .
.
где α - коэффициент растяжения (положительное число, большее 1.0; можно употребить, например, значение 2.0), r - номер текущего шага алгоритма.
Координаты прочих вершин симплекса не изменяются.
Сжатие или растяжение симплекса выполняет следующая подпрограмма:
subroutine shrinking_expansion(simplex, k, alpha_beta, n)
real(8) simplex(n, n + 1)
real(8), intent(in) :: alpha_beta
integer, intent(in) :: k, n
real(8) xc(n)
xc = center_of_gravity(simplex, k, n)
simplex(:, k) = xc + alpha_beta * (simplex(:, k) - xc)
end subroutine shrinking_expansion
В случае сильно овражных функций может происходить вырождение (сплющивание) симплекса, что приводит к необходимости восстановления симплекса, которое заключается в следующем:
Восстановление симплекса выполняет следующая подпрограмма:
! Восстанавливает симплекс
subroutine simplexRestore()
real(8) fmi
real(8) X2(n)
integer imi(1), imi2(1)
fmi = minval(fn)
imi = minloc(fn)
imi2 = minloc(fn, fn /= fmi)
X2 = simplex(:, imi(1)) - simplex(:, imi2(1))
call makeSimplex(simplex(:, imi(1)), sqrt(dot_product(X2, X2)), n)
end subroutine simplexRestore
В главной программе задаются параметры алгоритма и начальный симплекс (регулярный). Оптимизируемая функция объявляется в главной программе с атрибутом External и поэтому может быть использована в качестве параметра процедуры.
program tst
integer, parameter :: n = 2
real(8) X(n), L, L_thres, cR, alpha, beta, gamma
real(8), external :: Rosenbrock
L = 0.4_8 ! Начальная длина ребра симплекса
L_thres = 1.0e-5_8 ! Предельное значение длины ребра симплекса
cR = 1.0_8 ! Коэффициент отражения симплекса
alpha = 2.0_8 ! Коэффициент растяжения симплекса
beta = 0.5_8 ! Коэффициент сжатия симплекса
gamma = 0.5_8 ! Коэффициент редукции симплекса
! Первая вершина начального симплекса (начальная точка)
X(1) = 5.0_8
X(2) = -5.0_8
print *, 'Start point = ', X
!
! Поиск минимума функции Розенброка
call nelMead(Rosenbrock, X, n, L, L_thres, cR, alpha, beta, gamma)
!
! Результат
print *, 'Result = ', X
end program tst
!
! Выполняет поиск экстремума (минимума) функции F
subroutine nelMead(F, X, n, L, L_thres, cR, alpha, beta, gamma)
real(8) F, X(n), L, L_thres, cR, alpha, beta, gamma
integer n, j, jMx, i
real(8) X_R(n), simplex(n, n + 1), FN(n + 1)
real(8) Fmi, Fma, F_R, F_S, F_E
integer ima(1), k, kr
! kr_todo - число шагов алгоритма, после выполнения которых симплекс восстанавливается
integer, parameter :: kr_todo = 60
j = 0
! Предельное число шагов алгоритма (убрать после отладки)
jMx = 10000
print *, 'L = ', L
print *, 'L_thres = ', L_thres
print *, 'cR = ', cR
print *, 'alpha = ', alpha
print *, 'beta = ', beta
print *, 'gamma = ', gamma
call makeSimplex(X, L, n)
kr = 0
k = 1
do while (notStopYet() .and. j < jMx)
j = j + 1
kr = kr + 1
if (kr == kr_todo) then
kr = 0
! Восстановление симплекса
call simplexRestore()
end if
Fmi = minval(FN)
Fma = maxval(FN)
ima = maxloc(FN)
! Номер отражаемой вершины
k = ima(1)
X = simplex(:, k)
! Отражение
call reflection(simplex, k, cR, n)
X_R = simplex(:, k)
! Значение функции в вершине k симплекса после отражения
F_R = F(simplex(:, k), n)
if (F_R > Fma) then
! Сжатие
call shrinking_expansion(simplex, k, beta, n)
! Значение функции в вершине k симплекса после его сжатия
F_S = F(simplex(:, k), n)
if (F_S > Fma) then
simplex(:, k) = X
! Редукция
call reduction(simplex, k, gamma, n)
do i = 1, n + 1
if (i == k) cycle
! Значения функций в вершинах симплекса после редукции
! В вершине k значение функции сохраняется
FN(i) = F(simplex(:, i), n)
end do
else
FN(k) = F_S
end if
else if (F_R < Fmi) then
! Растяжение
call shrinking_expansion(simplex, k, alpha, n)
! Значение функции в вершине k симплекса после его растяжения
F_E = F(simplex(:, k), n)
if (F_E > Fmi) then
simplex(:, k) = X_R
FN(k) = F_R
else
FN(k) = F_E
end if
else
FN(k) = F_R
end if
end do
! Результат
print *, 'Number of iterations j = ', j
contains
!
! Возвращает .true., если длина хотя бы одного ребра симплекса превышает L_thres,
! или .false. - в противном случае
logical function notStopYet()
integer i, j
real(8) X(n), X2(n)
notStopYet = .false.
do i = 1, n
X = simplex(:, i)
do j = i + 1, n + 1
X2 = X - simplex(:, j)
if (sqrt(dot_product(X2, X2)) > L_thres) then
notStopYet = .true.
return
end if
end do
end do
end function notStopYet
!
! Второй вариант определения точки останова алгоритма
! Возвращает .true., если хотя бы одна разница значений функций в вершинах симплекса превышает L_thres,
! или .false. - в противном случае
logical function notStopYet2()
integer i, j
real(8) fv
notStopYet2 = .false.
do i = 1, n
fv = FN(i)
do j = i + 1, n + 1
if (abs(fv - FN(j)) > L_thres) then
notStopYet2 = .true.
return
end if
end do
end do
end function notStopYet2
!
! Восстанавливает симплекс
subroutine simplexRestore()
real(8) fmi
real(8) X2(n)
integer imi(1), imi2(1)
fmi = minval(fn)
imi = minloc(fn)
imi2 = minloc(fn, fn /= fmi)
X2 = simplex(:, imi(1)) - simplex(:, imi2(1))
call makeSimplex(simplex(:, imi(1)), sqrt(dot_product(X2, X2)), n)
end subroutine simplexRestore
!
! Создает из точки X регулярный симплекс с длиной ребра L и с n + 1 вершиной
subroutine makeSimplex(X, L, n)
real(8) X(:), L
integer n
real(8) qn, q2, r1, r2
qn = sqrt(1.0_8 + n) - 1.0_8
q2 = L / sqrt(2.0_8) * n
r1 = q2 * (qn + n)
r2 = q2 * qn
simplex(:, 1) = X
do i = 2, n + 1
simplex(:, i) = X + r2
end do
do i = 2, n + 1
simplex(i - 1, i) = simplex(i - 1, i) - r2 + r1
end do
do i = 1, n + 1
! Значения функции в вершинах созданного симплекса
FN(i) = F(simplex(:, i), n)
end do
end subroutine makeSimplex
!
! Вычисляет центр тяжести симплекса
function center_of_gravity(simplex, k, n)
real(8) center_of_gravity(n)
real(8), intent(in) :: simplex(n, n + 1)
integer, intent(in) :: k, n
integer j
do j = 1, n
center_of_gravity(j) = sum(simplex(j, :))
end do
center_of_gravity = (center_of_gravity - simplex(:, k)) / n
end function center_of_gravity
!
! Выполняет операцию отражения
subroutine reflection(simplex, k, cR, n)
real(8) simplex(n, n + 1)
! cR - коэффициент отражения
real(8), intent(in) :: cR
integer, intent(in) :: k, n
simplex(:, k) = (1 +cR) * center_of_gravity(simplex, k, n) - simplex(:, k)
end subroutine reflection
!
! Обеспечивает редукцию симплекса
subroutine reduction(simplex, k, gamma, n)
real(8) simplex(n, n + 1)
real(8), intent(in) :: gamma
integer, intent(in) :: k, n
real(8) xk(n)
integer j
xk = simplex(:, k)
do j = 1, n
simplex(:, j) = xk + gamma * (simplex(:, j) - xk)
end do
simplex(:, k) = xk
end subroutine reduction
!
! Растяжение или сжатие симплекса
subroutine shrinking_expansion(simplex, k, alpha_beta, n)
real(8) simplex(n, n + 1)
real(8), intent(in) :: alpha_beta
integer, intent(in) :: k, n
real(8) xc(n)
xc = center_of_gravity(simplex, k, n)
simplex(:, k) = xc + alpha_beta * (simplex(:, k) - xc)
end subroutine shrinking_expansion
end subroutine nelMead
!
real(8) function Rosenbrock(X, n)
real(8) X(n)
integer n
Rosenbrock = (1.0_8 - X(1))**2 + 100.0_8 * (X(2) - X(1) * X(1) )**2
end function Rosenbrock
Второй вариант определения точки останова алгоритма реализуется функцией notStopYet2, которая возвращает .true., если хотя бы одна разница значений функций в различных вершинах симплекса превышает L_thres. В противном случае функция вернет .false.
using System;
using System.IO; // StreamReader
using System.Windows.Forms;
namespace WindowsFormsApplicationNelderMid
{
public partial class FormNelderMid : Form
{
const int NP = 2; // NP - число аргументов функции
double[,] simplex = new double[NP, NP + 1]; // NP + 1 - число вершин симплекса
double[] FN = new double[NP + 1];
StreamWriter sW = new StreamWriter("res.txt");
public FormNelderMid()
{
InitializeComponent();
}
private double F(double[] X, int NP) // Функциия Розенброка
{
double x1 = X[0];
double p = 1.0 - x1;
double p2 = X[1] - x1 * x1;
return p * p + 100.0 * p2 * p2;
}
// Создает из точки X регулярный симплекс с длиной ребра L и с NP + 1 вершиной
// Формирует массив FN значений оптимизируемой функции F в вершинах симплекса
private void makeSimplex(double[] X, double L, int NP, bool first)
{
double qn, q2, r1, r2;
int i, j;
qn = Math.Sqrt(1.0 + NP) - 1.0;
q2 = L / Math.Sqrt(2.0) * (double)NP;
r1 = q2 * (qn + (double)NP);
r2 = q2 * qn;
for(i = 0; i < NP; i++) simplex[i, 0] = X[i];
for(i = 1; i < NP + 1; i++)
for(j = 0; j < NP; j++)
simplex[j, i] = X[j] + r2;
for(i = 1; i < NP + 1; i++) simplex[i - 1, i] = simplex[i - 1, i] - r2 + r1;
for(i = 0; i < NP + 1; i++)
{
for(j = 0; j < NP; j++) X[j] = simplex[j, i];
FN[i] = F(X, NP); // Значения функции в вершинах начального симплекса
}
if (first)
{
sW.WriteLine("Значения функции в вершинах начального симплекса:");
for (i = 0; i < NP + 1; i++) sW.WriteLine(FN[i]);
}
}
private double[] center_of_gravity(int k, int NP) // Центр тяжести симплекса
{
int i, j;
double s;
double[] xc = new double[NP];
for (i = 0; i < NP; i++)
{
s = 0;
for (j = 0; j < NP + 1; j++) s += simplex[i, j];
xc[i] = s;
}
for (i = 0; i < NP; i++) xc[i] = (xc[i] - simplex[i, k]) / (double) NP;
return xc;
}
private void reflection(int k, double cR, int NP) // Отражение вершины с номером k относительно центра тяжести
{
double[] xc = center_of_gravity(k, NP); // cR – коэффициент отражения
for (int i = 0; i < NP; i++) simplex[i, k] = (1.0 + cR) * xc[i] - simplex[i, k];
}
private void reduction(int k, double gamma, int NP) // Редукция симплекса к вершине k
{
int i, j; // gamma – коэффициент редукции
double[] xk = new double[NP];
for (i = 0; i < NP; i++) xk[i] = simplex[i, k];
for (j = 0; j < NP; j++)
for (i = 0; i < NP; i++)
simplex[i, j] = xk[i] + gamma * (simplex[i, j] - xk[i]);
for (i = 0; i < NP; i++) simplex[i, k] = xk[i]; // Восстанавливаем симплекс в вершине k
}
private void shrinking_expansion(int k, double alpha_beta, int NP) // Сжатие/растяжение симплекса. alpha_beta – коэффициент растяжения/сжатия
{
double[] xc = center_of_gravity(k, NP);
for (int i = 0; i < NP; i++)
simplex[i, k] = xc[i] + alpha_beta * (simplex[i, k] - xc[i]);
}
private double findL(double[] X2, int NP) // Длиина ребра симплекса
{
double L = 0;
for (int i = 0; i < NP; i++) L += X2[i] * X2[i];
return Math.Sqrt(L);
}
private double minval(double[] F, int N1, ref int imi) // Минимальный элемент массива и его индекс
{
double fmi = double.MaxValue, f;
for (int i = 0; i < N1; i++)
{
f = F[i];
if (f < fmi)
{
fmi = f;
imi = i;
}
}
return fmi;
}
private double maxval(double[] F, int N1, ref int ima) // Максимальный элемент массива и его индекс
{
double fma = double.MinValue, f;
for (int i = 0; i < N1; i++)
{
f = F[i];
if (f > fma)
{
fma = f;
ima = i;
}
}
return fma;
}
private void simplexRestore(int NP) // Восстанавление симплекса
{
int i, imi = -1, imi2 = -1;
double fmi, fmi2 = double.MaxValue, f;
double[] X = new double[NP], X2 = new double[NP];
fmi = minval(FN, NP + 1, ref imi);
for (i = 0; i < NP + 1; i++)
{
f = FN[i];
if (f != fmi && f < fmi2)
{
fmi2 = f;
imi2 = i;
}
}
for (i = 0; i < NP; i++)
{
X[i] = simplex[i, imi];
X2[i] = simplex[i, imi] - simplex[i, imi2];
}
makeSimplex(X, findL(X2, NP), NP, false);
}
private bool notStopYet(double L_thres, int NP) // Возвращает true, если длина хотя бы одного ребра симплекса превышает L_thres, или false - в противном случае
{
int i, j, k;
double[] X = new double[NP], X2 = new double[NP];
for (i = 0; i < NP; i++)
{
for (j = 0; j < NP; j++) X[j] = simplex[j, i];
for (j = i + 1 ; j < NP + 1; j++)
{
for (k = 0; k < NP; k++) X2[k] = X[k] - simplex[k, j];
if (findL(X2, NP) > L_thres) return true;
}
}
return false;
}
// Выполняет поиск экстремума (минимума) функции F
private void nelMead(ref double[] X, int NP, double L, double L_thres, double cR, double alpha, double beta, double gamma)
{
int i, j2, imi = -1, ima = -1;
int j = 0, kr = 0, jMx = 10000; // Предельное число шагов алгоритма (убрать после отладки)
double[] X2 = new double[NP], X_R = new double[NP];
double Fmi, Fma, F_R, F_S, F_E;
const int kr_todo = 60; // kr_todo - число шагов алгоритма, после выполнения которых симплекс восстанавливается
sW.WriteLine("L = " + L);
sW.WriteLine("L_thres = " + L_thres);
sW.WriteLine("cR = " + cR);
sW.WriteLine("alpha = " + alpha);
sW.WriteLine("beta = " + beta);
sW.WriteLine("gamma = " + gamma);
makeSimplex(X, L, NP, true);
while (notStopYet(L_thres, NP) && j < jMx)
{
j++; // Число итераций
kr++;
if (kr == kr_todo)
{
kr = 0;
simplexRestore(NP); // Восстановление симплекса
}
Fmi = minval(FN, NP + 1, ref imi);
Fma = maxval(FN, NP + 1, ref ima); // ima - Номер отражаемой вершины
for (i = 0; i < NP; i++) X[i] = simplex[i, ima];
reflection(ima, cR, NP); // Отражение
for (i = 0; i < NP; i++) X_R[i] = simplex[i, ima];
F_R = F(X_R, NP); // Значение функции в вершине ima симплекса после отражения
if (F_R > Fma)
{
shrinking_expansion(ima, beta, NP); // Сжатие
for (i = 0; i < NP; i++) X2[i] = simplex[i, ima];
F_S = F(X2, NP); // Значение функции в вершине ima симплекса после его сжатия
if (F_S > Fma)
{
for (i = 0; i < NP; i++) simplex[i, ima] = X[i];
reduction(ima, gamma, NP); // Редукция
for (i = 0; i < NP + 1; i++)
{
if (i == ima) continue;
for (j2 = 0; j2 < NP; j2++) X2[j2] = simplex[j2, i];
// Значения функций в вершинах симплекса после редукции. В вершине ima значение функции сохраняется
FN[i] = F(X2, NP);
}
}
else
FN[ima] = F_S;
}
else if (F_R < Fmi)
{
shrinking_expansion(ima, alpha, NP); // Растяжение
for (j2 = 0; j2 < NP; j2++) X2[j2] = simplex[j2, ima];
F_E = F(X2, NP); // Значение функции в вершине ima симплекса после его растяжения
if (F_E > Fmi)
{
for (j2 = 0; j2 < NP; j2++) simplex[j2, ima] = X_R[j2];
FN[ima] = F_R;
}
else
FN[ima] = F_E;
}
else
FN[ima] = F_R;
}
sW.WriteLine("Число итераций: " + j);
}
private void Go_Click(object sender, EventArgs e)
{
// -2.048, 2.048
// -5.0, 10.0
double[] X = { -2.048, 2.048 }; // Первая вершина начального симплекса (начальная точка)
double L, L_thres, cR, alpha, beta, gamma;
L = 0.4; // Начальная длина ребра симплекса
L_thres = 1.0e-5; // Предельное значение длины ребра симплекса
cR = 1.0; // Коэффициент отражения симплекса
alpha = 2.0; // Коэффициент растяжения симплекса
beta = 0.5; // Коэффициент сжатия симплекса
gamma = 0.5; // Коэффициент редукции симплекса
sW.WriteLine("Начальная точка:"); // Результат
for (int i = 0; i < NP; i++) sW.WriteLine(X[i]);
nelMead(ref X, NP, L, L_thres, cR, alpha, beta, gamma); // Поиск минимума функции Розенброка
sW.WriteLine("Результат:");
sW.WriteLine("Аргументы:");
for (int i = 0; i < NP; i++) sW.WriteLine(X[i]);
sW.WriteLine("Функция в вершинах симплекса:");
for (int i = 0; i < NP + 1; i++) sW.WriteLine(FN[i]);
sW.Close();
MessageBox.Show("Готово");
}
private void buttonClose_Click(object sender, EventArgs e)
{
Close();
}
}
}
Используется библиотека SciPy [2]. Реализуются два варианта вызова библиотечной процедуры оптимизации:
# Вариант 1
import numpy as np
import math # Для sqrt()
import scipy.optimize as opt
# Функция Розенброка
def Rosenbrock(X):
return (1.0 - X[0])**2 + 100.0_8 * (X[1] - X[0] * X[0] )**2
#
n = 2
x0 = np.zeros(2, dtype = float) # Вектор с двумя элементами типа float
# Начальная точка поиска минимума функции
x0[0] = 5.0
x0[1] = -5.0
xtol = 1.0e-5 # Точность поиска экстремума
# Находим минимум функции
res = opt.minimize(Rosenbrock, x0, method = 'Nelder-Mead', options = {'xtol': xtol, 'disp': True})
print(res)
Результат:
final_simplex: (array([[0.99999804, 0.99999609],
[1.00000156, 1.0000033 ],
[1.00000214, 1.00000398]]), array([3.84730933e-12, 5.66678063e-12, 1.41233808e-11]))
fun: 3.847309326090408e-12
message: 'Optimization terminated successfully.'
nfev: 135
nit: 70
status: 0
success: True
x: array([0.99999804, 0.99999609])
# Вариант 2
import numpy as np
import math # Для sqrt()
import scipy.optimize as opt
# Функция Розенброка
def Rosenbrock(X):
return (1.0 - X[0])**2 + 100.0_8 * (X[1] - X[0] * X[0] )**2
#
# Процедура формирования начального симплекса
def makeInitialSimplex(X, L, n, initialSimplex):
qn = math.sqrt(1.0 + n) - 1.0
q2 = L / math.sqrt(2.0) * n
r1 = q2 * (qn + n)
r2 = q2 * qn
initialSimplex[0, :] = X
for j in range(n):
initialSimplex[j + 1, :] = X + r2
for i in range(n):
initialSimplex[i + 1, i] += (r1 - r2)
#
n = 2
x0 = np.zeros(2, dtype = float) # Вектор с двумя элементами типа float
# Начальная точка поиска минимума функции
x0[0] = 5.0
x0[1] = -5.0
xtol = 1.0e-5 # Точность поиска экстремума
# Начальная симплекс поиска минимума функции
initialSimplex = np.zeros((n + 1, n), dtype = float)
L = 0.4 # Длина ребра начального симплекса
# Формируем начальный симплекс
makeInitialSimplex(x0, L, n, initialSimplex)
# Находим минимум функции
res = opt.minimize(Rosenbrock, x0, method = 'Nelder-Mead', options = {'xtol': xtol, 'disp': True, 'initial_simplex': initialSimplex})
print(res)
Результат:
final_simplex: (array([[0.99999847, 0.99999698],
[1.00000191, 1.00000346],
[0.99999669, 0.99999303]]), array([2.47098051e-12, 1.69748815e-11, 2.25735805e-11]))
fun: 2.4709805087558158e-12
message: 'Optimization terminated successfully.'
nfev: 158
nit: 83
status: 0
success: True
x: array([0.99999847, 0.99999698])
При испытании программы поиск минимума функции Розенброка начинался с различных точек. Во всех случаях минимум был обнаружен.
Точность поиска равна 1.0e-5.
Точки брались следующие:
В случае начальной точки (2.0, -2.0) минимум не будет достигнут (Фортран / C#), если отказаться от восстановления симплекса.
Так же в случае Фортрана минимум не будет найден, если начать с точки (-5.0, 5.0) и употребить восстановление симплекса.