Тестирование метода Хука-Дживса на функции Розенброка показало его чувствительность к выбору начальной точки поиска экстремума функции.
В этой работе, опять же на функции Розенброка, реализуется и тестируется метод Нелдера-Мида [1].
Приводится Python-реализации поиска минимума функции методом Нелдера-Мида.
При желании можно познакомиться и с Фортран-, и C#-реализациями метода Нелдера-Мида.
Замечание. Для поиска максимума нужно умножить на -1 результат, получаемый при вычислении значения оптимизируемой функции.
В качестве тестовой берется функция Розенброка:
f(x1, x2) = (1 – x1)2 + 100 * (x2 – x12)2
Глобальный минимум функции равен 0.0 и находится в точке (x1, x2) = (1.0, 1.0).
При работе с функцией Розенброка для проверки используемого метода в качестве начальной часто берут точку
(-5, 10)
или точку
(-2.048, 2.048).
Приводимая программа может работать с произвольной оптимизируемой функцией.
Код, реализующий метод Нелдера-Мида, предваряет Python-программа построения графика функции Розенброка.
Выводится изометрическая проекция 3d-поверхности. Используется библиотека Matplotlib [2].
График показан на рис. 1.
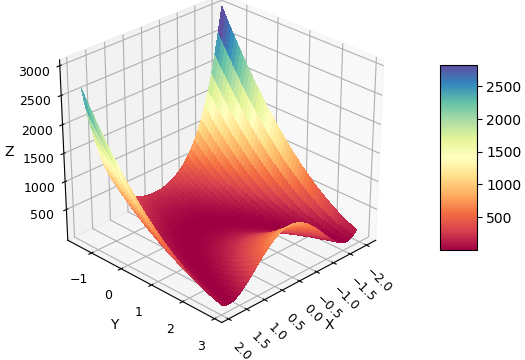
Рис. 1. График функции Розенброка
Для его вывода употреблен следующий код:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np
# Формирование сетки
X = np.arange(-2, 2, 0.1)
Y = np.arange(-1.5, 3, 0.1)
X, Y = np.meshgrid(X, Y)
# Функция Розенброка
Z = (1.0 - X)**2 + 100.0 * (Y - X * X)**2
#
fig = plt.figure()
# Будем выводить 3d-проекцию графика функции
ax = fig.gca(projection = '3d')
# Вывод поверхности
surf = ax.plot_surface(X, Y, Z, cmap = cm.Spectral, linewidth = 0, antialiased = False)
# Метки осей координат
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# Настройка оси X
for label in ax.xaxis.get_ticklabels():
label.set_color('black')
label.set_rotation(-45)
label.set_fontsize(9)
# Настройка оси Y
for label in ax.yaxis.get_ticklabels():
label.set_fontsize(9)
# Настройка оси Z
for label in ax.zaxis.get_ticklabels():
label.set_fontsize(9)
# Изометрия
ax.view_init(elev = 30, azim = 45)
# Шкала цветов
fig.colorbar(surf, shrink = 0.5, aspect = 5)
# Отображение результата (рис. 1)
plt.show()
Используется библиотека SciPy [3]. Реализуются два варианта вызова библиотечной процедуры оптимизации:
# Вариант 1
import numpy as np
import math # Для sqrt()
import scipy.optimize as opt
# Функция Розенброка
def Rosenbrock(X):
return (1.0 - X[0])**2 + 100.0_8 * (X[1] - X[0] * X[0] )**2
#
n = 2
x0 = np.zeros(2, dtype = float) # Вектор с двумя элементами типа float
# Начальная точка поиска минимума функции
x0[0] = -5.0
x0[1] = 10.0
xtol = 1.0e-5 # Точность поиска экстремума
# Находим минимум функции
res = opt.minimize(Rosenbrock, x0, method = 'Nelder-Mead', options = {'xtol': xtol, 'disp': True})
print(res)
Результат:
final_simplex: (array([[1.00000132, 1.0000028 ],
[1.00000014, 0.99999997],
[0.99999681, 0.99999355]]), array([4.38559817e-12, 9.00569749e-12, 1.05977059e-11]))
fun: 4.385598172677925e-12
message: 'Optimization terminated successfully.'
nfev: 269 (число оценок функции)
nit: 143 (число итераций)
status: 0
success: True
x: array([1.00000132, 1.0000028 ])
# Вариант 2
import numpy as np
import math # Для sqrt()
import scipy.optimize as opt
# Функция Розенброка
def Rosenbrock(X):
return (1.0 - X[0])**2 + 100.0_8 * (X[1] - X[0] * X[0] )**2
#
# Процедура формирования начального симплекса
def makeInitialSimplex(X, L, n, initialSimplex):
qn = math.sqrt(1.0 + n) - 1.0
q2 = L / math.sqrt(2.0) * n
r1 = q2 * (qn + n)
r2 = q2 * qn
initialSimplex[0, :] = X
for j in range(n):
initialSimplex[j + 1, :] = X + r2
for i in range(n):
initialSimplex[i + 1, i] += (r1 - r2)
#
n = 2
x0 = np.zeros(2, dtype = float) # Вектор с двумя элементами типа float
# Начальная точка поиска минимума функции
x0[0] = -5.0
x0[1] = 10.0
xtol = 1.0e-5 # Точность поиска экстремума
# Начальная симплекс поиска минимума функции
initialSimplex = np.zeros((n + 1, n), dtype = float)
L = 0.4 # Длина ребра начального симплекса
# Формируем начальный симплекс
makeInitialSimplex(x0, L, n, initialSimplex)
# Находим минимум функции
res = opt.minimize(Rosenbrock, x0, method = 'Nelder-Mead', options = {'xtol': xtol, 'disp': True, 'initial_simplex': initialSimplex})
print(res)
Результат:
final_simplex: (array([[1.00000168, 1.00000305],
[0.99999702, 0.99999376],
[0.99999679, 0.99999416]]), array([1.18711392e-11, 1.70297440e-11, 4.41663303e-11]))
fun: 1.1871139195622139e-11
message: 'Optimization terminated successfully.'
nfev: 255 (число оценок функции)
nit: 138 (число итераций)
status: 0
success: True
x: array([1.00000168, 1.00000305])