В задаче прямого зондирования ионосферы ищутся такие значений частоты и угла излучения декаметрового (коротковолнового, КВ) сигнала, при которых отраженный ионосферой сигнал пересекает поверхность Земли в окрестности заданной точки (приемника).
В геометрической модели сигнал представляется в виде луча.
В процессе решения задачи прямого зондирования ионосферы рассчитываются точка входа луча в ионосферу, траектория и время нахождения луча в ионосфере, точка выхода луча из ионосферы и точка пересечения луча с поверхностью Земли.
Также выявляются следующие ситуации:
Используется 2d-геометрическая модель распространения луча. Плоскость, в которой решается задача, проходит через центр Земли и расположенные на поверхности Земли источник и приемник.
Траектория луча и время пребывания сигнала в ионосфере определяются в результате решения системы дифференциальных уравнений. Рассматривается упрощенная система, не учитывающая магнитное поле Земли и омическое затухание сигнала. Решение системы дифференциальных уравнений выполняется средствами математической библиотеки IMSL.
Для тестирования программ используется параболическая модель ионосферы. Полученные результаты сравниваются с известными, аналитически полученными значениями.
Язык программирования Фортран. Сопровождающие текст рисунки созданы в 3ds Max при помощи написанных на MAXSript программ, код которых приведен в приложении 2.
Пусть известны координаты расположенных на поверхности Земли источника и приемника КВ сигнала и направление этого сигнала.
Сигнал распространяется от источника к приемнику в плоскости, проходящей через центр Земли, источник и приемник.
Требуется найти частоту f, при которой сигнал достигнет приемника, а также траекторию и время распространения сигнала от источника к приемнику.
Задачу иллюстрирует рис. 1.
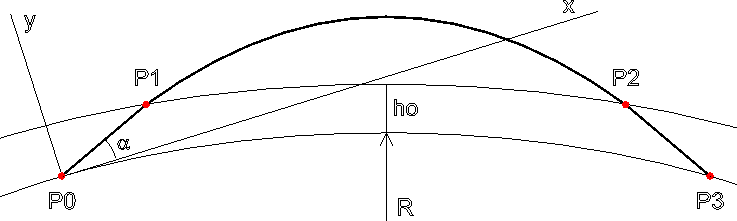
Рис. 1. Траектория луча и система координат зондирования
В пути, проходимым лучом, есть три части:
S01 - от источника до входа в ионосферу;
S12 - путь в ионосфере;
S23 - от точки выхода из ионосферы к приемнику.
Расчет пути выполняется в системе координат зондирования (СКЗ), начало которой совпадает с точкой размещения источника сигнала (точка P0 на рис. 1), ось X касается поверхности Земли, обе оси находятся в плоскости, проходящей через центр Земли, источник и приемник.
Угол α между лучом и осью Х СКЗ будем называть углом зондирования.
Используются три системы координат: СКЗ (двумерная, см. рис. 1) и трехмерная мировая система координат (МСК), центр которой совпадает с центром Земли (рис. 2).
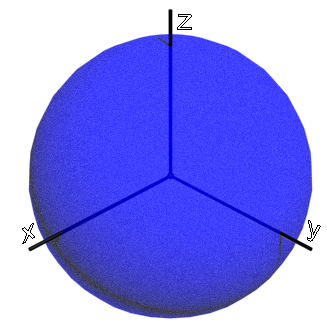
Рис. 2. Мировая система координат
В МСК долгота и широта на положительном направлении оси X равны нулю.
В СКЗ (см. рис. 1) центр Земли имеет координаты [0, -(R + h)], где R - это радиус Земли, а h - высота источника над уровнем моря (на рис. 1 h = 0).
Координаты источника и приемника задаются в МСК. Затем они определяются в СКЗ, в которой и выполняется весь последующий расчет.
Задача решается в СКЗ. Используются следующие обозначения:
R - радиус Земли;
hp - высота приемника над уровнем моря;
h0 - начальная высота ионосферы.
Задача решается в следующем порядке:
Данные, используемые различными процедурами, собраны в модуле commonParams.
Координаты источника и приемника в МСК находятся по их географическим координатам (рис. 3).
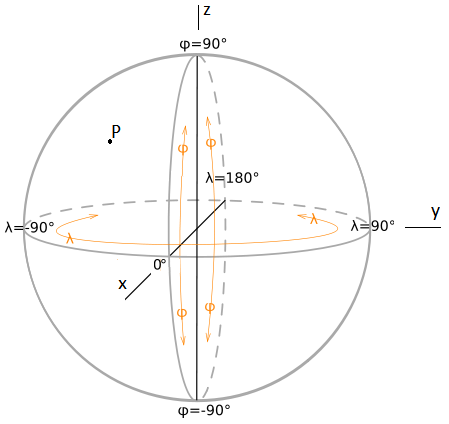
Рис. 3. Диапазоны изменения географических координат (долготы и широты)
Будем полагать, что Земля - это сфера радиуса R.
Найдем по широте φ и долготе λ точки на поверхности Земли найти ее координаты в МСК. Высота над уровнем моря в заданной точке равна h.
В МСК проекция точки P на плоскость X0Y равна
(R + h) cosφ
Поэтому в МСК
xp = (R + h) cosφ cosλ
yp = (R + h) cosφ sinλ
zp = (R + h) sinφ
В СКЗ источник имеет координаты [0, 0].
Координаты приемника в СКЗ можно найти по известным географическим координатам источника и приемника.
Пусть в МСК источник S и приемник P имеют соответственно координаты
[xs, ys, zs] и [xp, yp, zp].
Угол межу источником и приемником равен
α = acos(dot_product (normalize vs) (normalize vp)),
где vs и vp - векторы, начинающиеся в начале МСК и завершающиеся соответственно в точках
[xs, ys, zs] и [xp, yp, zp];
normalize - функция, возвращающая нормализованные координаты вектора;
dot_product - функция, возвращающая скалярное произведение векторов-аргументов функции.
Зная угол α (рис. 4) и высоты hs и hp источника и приемника над уровнем моря, найдем координаты приемника в СКЗ.
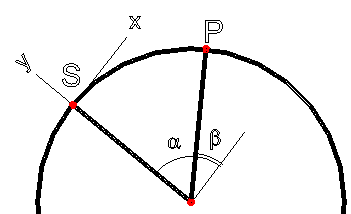
Рис. 4. Вычисление координат приемника в СКЗ (на рисунке hs = hp = 0)
β = 90 - α
xp = (R + hp) cosβ
yp = (R + hp) sinβ - (R + hs)
Расстояние SP между источником и приемником (дальность распространения сигнала по Земле) принимается равным
SP = (R + 0.5 (hs + hp)) * α (угол α берется в радианах)
Координаты приемника в СКЗ вычисляет следующая процедура:
!
! Вычисляет
! - угол между источником и приемником
! - координаты приемника в СКЗ
! - расстояние по Земле между источником и приемником
subroutine fndRcvrCrds()
use commonParams
implicit none
real(8) arrSrcWrldCrds(3), arrRcvrWrldCrds(3)
call gToWrld(hS, srcGCrds, arrSrcWrldCrds)
call gToWrld(hP, rcvrGCrds, arrRcvrWrldCrds)
!
! Угол между источником и приемником (в радианах)
srcRcvrNgl = acos(dot_product(nrmls(arrSrcWrldCrds), nrmls(arrRcvrWrldCrds)))
! Координаты приемника в СКЗ, км
rcvrCrds%x = (rRth + hP) * cos(0.5_8 * pi - srcRcvrNgl)
rcvrCrds%y = (rRth + hP) * sin(0.5_8 * pi - srcRcvrNgl) - (rRth + hs)
! Расстояние по земле между источником и приемником, км
srcRcvrErthDstnc = (rRth + 0.5 * (hs + hp)) * srcRcvrNgl
if (chckDt) then
! Угол между источником и приемником (вычисляем в радианах, выводим в градусах)
print '(a13, f9.4)', 'srcRcvrNgl = ', 180.0_8 * srcRcvrNgl / pi
! Координаты приемника в СКЗ, км
print '(a11, 2f9.2)', 'rcvrCrds = ', rcvrCrds
! Расстояние по Земле между источником и приемником, км
print '(a19, f9.2)', 'srcRcvrErthDstnc = ', srcRcvrErthDstnc
end if
contains
!
! Преобразование географических координат точки в мировые
subroutine gToWrld(h, gCrds, arrCrds)
real(8) h, arrCrds(3)
type(pnt) gCrds
arrCrds(1) = (rRth + h) * cosD(gCrds%x) * cosD(gCrds%y)
arrCrds(2) = (rRth + h) * cosD(gCrds%x) * sinD(gCrds%y)
arrCrds(3) = (rRth + h) * sinD(gCrds%x)
end subroutine gToWrld
!
! Нормализация 3d-вектора
function nrmls(vctr)
real(8) nrmls(3), vctr(3), s
s = sqrt(dot_product(vctr, vctr))
nrmls = vctr / s
end function nrmls
end subroutine fndRcvrCrds
Основным фактором, влияющим на параметры сигнала, является концентрация электронов в отражающем слое ионосферы. Также на параметры сигнала оказывают влияние геомагнитное поле, омическое затухание и иные факторы.
Параболическая модель используется для отладки программы.
Модель определяет значение квадрата плазменной частоты (далее КПЧ) на заданной высоте h (h > h0) отражающего слоя ионосферы следующим образом:
f2N = f2c (1 - ((hm - h) / dh) 2),
где
h – текущая высота;
h0 – начальная высота ионосферы;
hm – высота, на которой электронная концентрация имеет максимальное значение;
dh = hm - h0 – полутолщина отражающего слоя ионосферы;
fc – критическая частота;
R – радиус Земли.
Замечание. Если известны концентрации электронов отражающего слоя, например в модели IRI [2], то критическая частота определяется по следующей формуле:
fc = [80.8Nm]0.5,
где Nm - максимальная концентрация электронов в исследуемой области отражающего слоя.
Параболическая модель применяется для тестирования программ, вычисляющих групповые пути сигнала, поскольку для нее известны точные решения.
При генерации массива КПЧ по параболической модели ионосферы использованы следующие значения:
hm = 140 км;
h0 = 90 км.
fc = 4 мГц;
R = 6370 км.
В расчете параметров сигнала используется квадрат плазменной частоты f2N, значение которого связано со значением концентрации электронов следующим образом:
N = 1.24*104f2N
Значения КПЧ берутся из модели ионосферы, например Международной модели IRI [2] (при отладке программы берется параболическая модель ионосферы).
Для сокращения времени вычислений в программе значение КПЧ в указанной точке ионосферы выполняется следующим образом:
Если требуется решать задачу в реальном масштабе времени, то массив КПЧ должен постоянно обновляться.
В области ионосферы между источником и приемником сигнала задаются nNgl * nH узловых точек (рис. 5), в которых в соответствии с моделью ионосферы вычисляются квадраты плазменной частоты (nNgl - число точек по углу; nH - число точек по высоте).
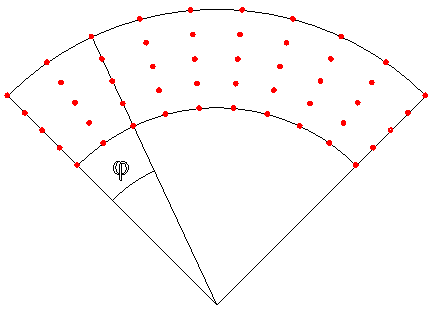
Рис. 5. Задание узловых точек для расчета квадратов плазменной частоты
Для задания угловой точки используются ее высота и угол φ между радиусами, проходящими через источник и текущую узловую точку.
Наряду с массивом arrF2N заполняется и массив arrXY координат точек в СКЗ, в которых вычисляется значения КПЧ. Массивы описаны в модуле commonParams.
!
! Генерирует, используя параболическую модель ионосферы,
! массив КПЧ в узловых точках отражающего слоя ионосферы
subroutine genArrF2N()
use commonParams
implicit none
integer i, j
real(8) dH, h, ngl
! Полутолщина отражающего слоя, км
dH = hM - h0
! Генерация массива КПЧ
! Увеличиваем размерность на 2 по каждому измерению для заполнения
! массивов частных производных КПЧ
allocate(arrF2N(0:nNgl + 1, 0:nH + 1), arrXY(0:nNgl + 1, 0:nH + 1))
! Шаг по высоте
sH = 2.0_8 * dH / (nH - 1)
! Текущая высота
h = h0 - sH
do j = 0, nH + 1
arrF2N(:, j) = f2Crtcl**2 * (1.0_8 - ((hM - h) / dH)**2)
h = h + sH
end do
! Массив arrXY в СКЗ
! Шаг по углу (srcRcvrNgl - угол в радианах между источником и приемником)
sNgl = srcRcvrNgl / (nNgl - 1)
! Текущий угол
ngl = -sNgl
do i = 0, nNgl + 1
h = rRth + h0 - sH
do j = 0, nH + 1
arrXY(i, j)%x = h * sin(ngl)
arrXY(i, j)%y = h * cos(ngl) - rRth - hS
h = h + sH
end do
ngl = ngl + sNgl
end do
! Проверочная печать
if (chckRrs) then
print '(3a9)', 'f2N', 'x', 'y'
do j = 0, nH + 1, 10
print '(3f9.2)', arrF2N(nNgl / 2, j), arrXY(nNgl / 2, j)
end do
end if
end subroutine genArrF2N
При расчете параметров сигнала необходимо также знать и значения частных производных КПЧ ∂f2N/∂x, ∂f2N/∂y. Эти значения вычисляются по интерполяционной схеме по известным значениям указанных частных производных в узловых точках модели ионосферы. Эти значения хранит массив arrDF2DXY, заполняемый следующей процедурой:
!
! Формирует массив частных производных КПЧ
subroutine fllNArrDF2NDXY()
use commonParams
implicit none
integer i, j
real(8) dF2Nx, dF2Ny, dx, dy
allocate(arrDF2NDXY(nNgl, nH))
do i = 1, nNgl
do j = 1, nH
dF2Nx = arrF2N(i - 1, j) - arrF2N(i + 1, j)
dx = arrXY(i - 1, j)%x - arrXY(i + 1, j)%x
dF2NY = arrF2N(i, j - 1) - arrF2N(i, j + 1)
dy = arrXY(i, j - 1)%y - arrXY(i, j + 1)%y
arrDF2NDXY(i, j)%x = dF2Nx / dx
arrDF2NDXY(i, j)%y = dF2Ny / dy
end do
end do
if (chckRrs) then
print '(4a10)', 'DF2NDXYx', 'DF2NDXYy', 'x', 'y'
do j = 1, nH, 10
print '(4f10.2)', arrDF2NDXY(nNgl / 2, j), arrXY(nNgl / 2, j)
end do
end if
end subroutine fllNArrDF2NDXY
Используется линейная интерполяции.
Пусть в СКЗ дана точка P отражающего слоя ионосферы с координатами [x, y] (рис. 6) и заполнены массивы квадратов плазменной частоты и координат узловых точек в СКЗ (соответственно массивы arrF2N и arrXY).
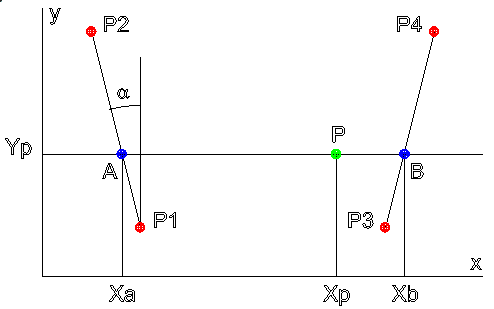
Рис. 6. Вычисление значения квадрата плазменной частоты в точке P
Пусть текущая точка Р окружена узловыми точками Р1, Р2, Р3 и Р4. Область, ограниченную этими точками будем называть областью окружения, а индексы в массиве arrXY нижней левой точки этой области – индексами области окружения.
Значение КПЧ в точке P = [xP, yP] будем вычислять следующим образом:
Последовательность вычислений:
cyA = (yP - yP1) / (yP2 - yP1)
f2NA = f2NP1 + cyA (f2NP2 - f2NP1)
cyB = (yP - yP3) / (yP4 - yP3)
f2NB = f2NP3 + cyB (f2NP4 - f2NP3)
tgα = (xP2 - xP1) / (yP2 - yP1)
xa = xP1 + (yP - yP1) tgα
tgα = (xP4 - xP3) / (yP4 - yP3)
xb = xP3 + (yP - yP3) tgα
cx = (xP - xa) / (xb - xa)
f2NP = f2NA + cx * (f2NB - f2NA)
Аналогичным образом по известным значениям частных производных КПЧ в узловых точках модели ионосферы вычисляются частные производные КПЧ в указанной точке отражающего слоя.
Заметим, что в программе употребляются лишь значения частных производных КПЧ, сами же значения КПЧ для вычислений не нужны. Они понадобятся, однако, при построении растровой карты ионосферы.
Приведенную последовательность вычислений реализует следующая процедура:
!
! Находит частные производные КПЧ (dF2NDXYCrrnt) в текущей точке траектории луча
subroutine fndDF2NDXYCrrnt()
use commonParams
implicit none
real(8) xP, yP, dyA, dyB, dyA12, dyB12, cyA, cyB, cx, xA, xB
type(pnt) p1, p2, p3, p4
type(pnt) dF2NP1DXY, dF2NP2DXY, dF2NP3DXY, dF2NP4DXY, dF2NADXY, dF2NBDXY
p1 = arrXY(iSrrnd, jSrrnd)
p2 = arrXY(iSrrnd, jSrrnd + 1)
p3 = arrXY(iSrrnd + 1, jSrrnd)
p4 = arrXY(iSrrnd + 1, jSrrnd + 1)
xP = arrBmPnts(nBmPnts)%x
yP = arrBmPnts(nBmPnts)%y
! Частные производные КПЧ узловых точек области окружения
dF2NP1DXY = arrDF2NDXY(iSrrnd, jSrrnd)
dF2NP2DXY = arrDF2NDXY(iSrrnd, jSrrnd + 1)
dF2NP3DXY = arrDF2NDXY(iSrrnd + 1, jSrrnd)
dF2NP4DXY = arrDF2NDXY(iSrrnd + 1, jSrrnd + 1)
dyA12 = p2%y - p1%y
dyA = yP - p1%y + dyA12
cyA = dyA / dyA12
dF2NADXY%x = dF2NP1DXY%x + cyA * (dF2NP2DXY%x - dF2NP1DXY%x)
dF2NADXY%y = dF2NP1DXY%y + cyA * (dF2NP2DXY%y - dF2NP1DXY%y)
dyB12 = p4%y - p3%y
dyB = yP - p3%y + dyB12
cyB = dyB / dyB12
dF2NBDXY%x = dF2NP3DXY%x + cyB * (dF2NP4DXY%x - dF2NP3DXY%x)
dF2NBDXY%y = dF2NP3DXY%y + cyB * (dF2NP4DXY%y - dF2NP3DXY%y)
xA = p1%x - dyA * (p2%x - p1%x) / dyA12
xB = p3%x - dyB * (p4%x - p3%x) / dyB12
cx = (xP - xA) / (xB - xA)
dF2NDXYCrrnt%x = dF2NADXY%x + cx * (dF2NBDXY%x - dF2NADXY%x)
dF2NDXYCrrnt%y = dF2NADXY%y + cx * (dF2NBDXY%y - dF2NADXY%y)
if (chckDF2NDXY) then
! Частные производные КПЧ в текущей точке траектории луча
print '(a15, 2f9.2)', 'dF2NDXYCrrnt = ', dF2NDXYCrrnt
! Частные производные КПЧ в узловых точках области окружения
print '(a12, 2f9.2)', 'dF2NP1DXY = ', dF2NP1DXY
print '(a17, 2f9.2)', 'dF2NP2DXY (j+) = ', dF2NP2DXY
print '(a17, 2f9.2)', 'dF2NP3DXY (i+) = ', dF2NP3DXY
print '(a21, 2f9.2)', 'dF2NP4DXY ((i+, j+) = ', dF2NP4DXY
end if
end subroutine fndDF2NDXYCrrnt
Начальные значения индексов области окружения определяются после вычисления координат точки входа луча в ионосферу следующей подпрограммой, в которой учтено, что начальный индекс окружения по высоте (jSrrnd) равен 1.
!
! Поиск начальных индексов области окружения
subroutine fndNtlIJSrrnd()
use commonParams
implicit none
integer i, j
real(8) xP, yP
type(pnt) pt
xP = arrBmPnts(1)%x
yP = arrBmPnts(1)%y
jSrrnd = 1
do i = 1, nNgl - 1
pt = arrXY(i, jSrrnd)
if (pt%x > xP) then
iSrrnd = i - 1
exit
end if
end do
if (chckDt) then
! Индексы области окружения точки входа луча в ионосферу
print '(2(a9, i3, 2x))', 'iSrrnd = ', iSrrnd, 'jSrrnd = ', jSrrnd
! Координаты узловых точек области окружения
print '(a26, 2f9.2)', 'arrXY(iSrrnd, jSrrnd) = ', arrXY(iSrrnd, jSrrnd)
print '(a26, 2f9.2)', 'arrXY(iSrrnd, jSrrnd+) = ', arrXY(iSrrnd, jSrrnd + 1)
print '(a26, 2f9.2)', 'arrXY(iSrrnd+, jSrrnd+) = ', arrXY(iSrrnd + 1, jSrrnd + 1)
print '(a26, 2f9.2)', 'arrXY(iSrrnd+, jSrrnd) = ', arrXY(iSrrnd + 1, jSrrnd)
end if
end subroutine fndNtlIJSrrnd
Индексы области окружения точки Рс найдем по ее известным координатам в СКЗ (рис. 7).
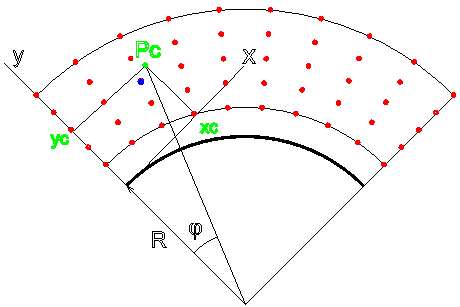
Рис. 7. Поиск индексов области окружения (индексов синей точки)
Очевидно, что
φ = arctg(xc / (R + hs + yc))
и
hс = (R + hs + yc) / cosφ - R,
где
[xc, yc] - координаты точки Pc в СКС;
hс - удаленность точки Pc от поверхности Земли;
R - радиус Земли;
hs - высота источника над уровнем моря.
Тогда индексы области окружения (индексы синей точки) равны:
iSrrnd = [φ / sNgl] + 1,
jSrrnd = [hc / sH] + 1,
[a] - целая часть числа a.
При этом, точка Pc оказывается за пределами взятого слоя ионосферы, если выполняется одно из следующих условий:
hc < h0;
hc > h0 + 2 dh;
φ > α,
где
h0 – начальная высота ионосферы;
dh – полутолщина отражающего слоя ионосферы;
α - угол между источником и приемником (см. рис. 4).
Поиск индексов области окружения обеспечит следующая подпрограмма:
!
! Поиск индексов области окружения текущей точки траектории луча
! Подпрограмма присвоит переменной cchRslt
! 0, если луч находится в исследуемой области ионосферы
! 1, если отраженный луч покинул ионосферу
! 2, если луч пробил верхнюю границу ионосферы
! 3, если луч пробил правую границу (prbNglsNtrvl%y) исследуемой области ионосферы
subroutine fndNtPnts()
use commonParams
implicit none
real(8) xC, yC, hC, nGl
type(pnt) p1, p2, p3
xC = arrBmPnts(nBmPnts)%x
yC = arrBmPnts(nBmPnts)%y
nGl = atan(xc / (rRth + hS + yC))
hC = (rRth + hS + yC) / cos(nGl) - rRth
if (hC < h0) then
! Отраженный луч покинул ионосферу и направился к Земле
cchRslt = 1
else if (hC >= 2.0_8 * hM - h0) then
! Луч пробил верхнюю границу ионосферы
cchRslt = 2
else if (nGl >= srcRcvrNgl) then
! Луч пробил правую границу исследуемой области ионосферы
cchRslt = 3
else
! Луч находится в исследуемой области ионосферы
cchRslt = 0
end if
iSrrnd = int(nGl / sNgl) + 1
jSrrnd = int((hc - h0) / sH) + 1
! Индексы области окружения текущей точки луча в ионосфере
!print '(2(a9, i3, 2x))', 'iSrrnd = ', iSrrnd, 'jSrrnd = ', jSrrnd
!print *, hC, h0
end subroutine fndNtPnts
Определим при заданных радиусе Земли R, высоте источника на уровнем моря hs, начальной высоте ионосферы h0 и угле зондирования α СКЗ-координаты точки Pe входа луча в ионосферу (рис. 8).
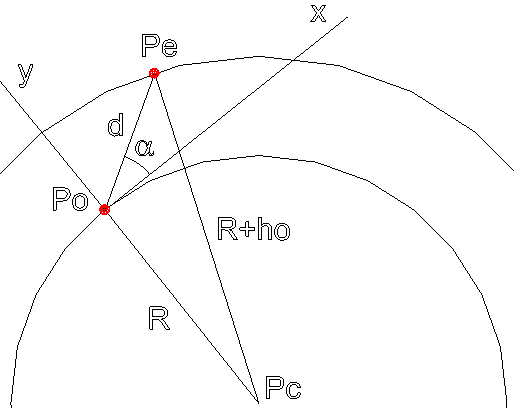
Рис. 8. Расчет координат точки входа луча в ионосферу (на рисунке hs = 0)
По теореме косинусов:
d^2 + (R + hs)^2 - 2 d (R + hs) cos(α + 90) = (R + ho)^2
Вычислив
d = -(R + hs) sinα + sqrt(((R + hs) sinα)^2 - (R + hs)^2 + (R + ho)^2),
найдем
Pe = [dcosα, dsinα]
Также координаты точки Pe можно найти из следующей системы уравнений:
x^2 + (y - (R + hs))^2 = (R + h0)^2
y = kx,
где k = tgα.
!
! Вычисляет координаты точки входа луча в ионосферу в СКЗ
subroutine fndBmNtrncCrds()
use commonParams
implicit none
real(8) d, snPrbNgl, rSn
snPrbNgl = sinD(prbNgl)
rSn = (rRth + hS) * snPrbNgl
d = -rSn + sqrt(rSn**2 - (rRth + hS)**2 +(rRth + h0)**2)
! Число точек в результирующей траектории луча
nBmPnts = 1
arrBmPnts(1)%x = d * cosD(prbNgl)
arrBmPnts(1)%y = d * snPrbNgl
if (chckDt) then
! Координаты в СКЗ точки входа луча в ионосферу, км
print '(a15, 2f9.2)', 'arrBmPnts(1) = ', arrBmPnts(1)
! Тест пройден, если rNtrnc = rRth + h0
print '(a22)', 'OK: rNtrnc = rRth + h0'
print '(a12, f9.2)', 'rNtrnc = ', sqrt(arrBmPnts(1)%x**2 + (arrBmPnts(1)%y + rRth + hS)**2)
print '(a12, f9.2)', 'rRth + h0 = ', rRth + h0
end if
end subroutine fndBmNtrncCrds
Расчет ведется в СКЗ. Известны координаты [x2, y2] точки Р2 выхода луча из ионосферы и угол β между лучом и осью Х в точке Р2 (рис. 9).
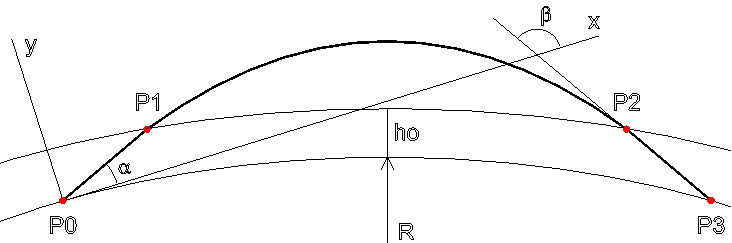
Рис. 9. Расчет координат [x3, y3] точки Р3 пересечения луча с поверхностью Земли
После выхода из ионосферы луч распространяется по прямой
x = k * y + x2 - k * y2,
где k = tgβ.
В точке пересечения с поверхностью Земли
x3 = k * y3 + x2 - k * y2
и
x3^2 + (y3 + R + hS)^2 = (R + hP)^2
Пусть
e = x2 - k * y2,
rS = R + hS,
rP = R + hP.
Тогда имеем следующее квадратное уравнение:
(1 + k^2) * y^2 + 2y * (k * e + rS) + rS^2 – rP^2 + e^2 = 0
Пусть
A = 1 + k^2,
B = k * e + rS,
C = rS^2 – rP^2 + e^2,
D = B^2 - A * C.
Тогда
y3 = -B ± sqrt(D) / A,
Решений может быть три:
а) луч с Землей не пересекается (D < 0),
б) луч касается Земли (D = 0),
в) две точки пересечения луча с Землей (D < 0); выбирается точка, которая ближе к точке выхода луча из ионосферы.
!
! Вычисляет в СКЗ координаты точки пересечения луча и Земли
! Возвращает .true., если луч пересекает поверхность Земли,
! или .false. - в противном случае
logical function fndBmRthCrssngCrds()
use commonParams
implicit none
real(8) xXt, yXt, cf, e, rS, rP, A, B, C, D
! Координаты в СКЗ точки выхода луча из ионосферы
xXt = arrBmPnts(nBmPnts)%x
yXt = arrBmPnts(nBmPnts)%y
cf = (arrBmPnts(nBmPnts - 1)%x - xXt) / (arrBmPnts(nBmPnts - 1)%y - yXt)
if (chckDt) then
print '(a25, 2f9.2)', 'arrBmPnts(nBmPnts) = ', arrBmPnts(nBmPnts)
print '(a25, 2f9.2)', 'arrBmPnts(nBmPnts - 1) = ', arrBmPnts(nBmPnts - 1)
end if
e = xXt - cf * yXt
rS = rRth + hS
rP = rRth + hP
A = 1.0_8 + cf * cf
B = cf * e + rS
C = rS**2 - rP**2 + e**2
D = B**2 - A * C
fndBmRthCrssngCrds = D > 0
if (fndBmRthCrssngCrds) then
! Выбираем ближайшую к источнику точку
crssngCrds%y = (-B + sqrt(D)) / A
crssngCrds%x = cf * crssngCrds%y + e
if (chckDt) then
! Координаты в СКЗ точки пересечения луча и Земли, км
print '(a13, 2f9.2)', 'crssngCrds = ', crssngCrds
! Координаты приемника в СКЗ, км
print '(a13, 2f9.2)', 'rcvrCrds = ', rcvrCrds
end if
end if
end function fndBmRthCrssngCrds
Полный групповой путь сигнала в атмосфере и ионосфере
SG = S01 + S12+ S23,
где
S01 = x1 sinα - расстояние от источника до точки входа в ионосферу (x1 - x-координата точки входа луча в ионосферу, α - угол зондирования);
S12 - длина пути в ионосфере;
S23 = sqrt((x3 - x2)^2 + (y3 - y2)^2) - расстояние от точки выхода луча из ионосферы до точки пересечения луча с поверхностью Земли.
Для вычисления S12 в программу вводится массив arrBmPnts, хранящий получаемые в процессе интегрирования текущие координаты луча в СКЗ (заполняется в подпрограмме fcn).
!
! Возвращает значение полного группового пути
real(8) function fndBmGrpPth()
use commonParams
implicit none
integer i
real(8) dx, dy, s12, s23
! Длина пути в ионосфере
s12 = 0.0_8
do i = 2, nBmPnts
dx = arrBmPnts(i - 1)%x - arrBmPnts(i)%x
dy = arrBmPnts(i - 1)%y - arrBmPnts(i)%y
s12 = s12 + sqrt(dx**2 + dy**2)
end do
dx = crssngCrds%x - arrBmPnts(nBmPnts)%x
dy = crssngCrds%y - arrBmPnts(nBmPnts)%y
s23 = sqrt(dx**2 + dy**2)
! prbNgl - yгол зондирования (в градусах)
! Полный групповой путь
fndBmGrpPth = arrBmPnts(1)%x * sinD(prbNgl) + s12 + s23
end function fndBmGrpPth
Параметры КВ сигнала (траекторию и время распространения), передаваемого через ионосферу, достаточно точно можно вычислить, решая прямую задачу Коши, задаваемую следующей системой обыкновенных дифференциальных уравнений с учетом влияния магнитного поля Земли:
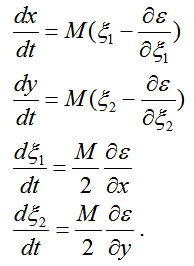
с начальными условиями
[x(0), y(0)] - координаты точки входа луча в ионосферу в СКЗ.
x'(0) = cosα,
y'(0) = sinα.
где α - угол зондирования.
Расчет ведется в СКЗ.
Диэлектрическая проницаемость среды
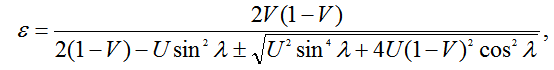
где
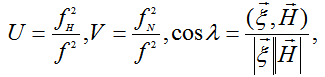
f - частота зондирования,
fH - гирочастота (угловая частота, с которой частица в однородном магнитном поле вращается вокруг силовой линии этого поля под действием силы Лоренца), может изменяться в пределах от 700 до 1600 кГц [3].
fN - плазменная частота (частота собственных продольных колебаний пространственного заряда в однородной плазме при отсутствии магнитного поля),
N = 1.24*104f2N,
где
N - концентрация электронов;
H = (H1, H2, H3) - вектор геомагнитного поля;
ξ = (ξ1, ξ2, ξ3) - вектор волновой нормали.
Коэффициент M выбирается таким образом, чтобы значение времени t распространения сигнала равнялось групповому пути [5]:
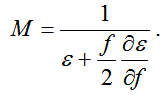
На траектории в ионосфере должно выполняться условие
ξ12 + ξ22 + ξ32 = ε.
Имеющийся в знаменателе формулы вычисления ε знак ± обусловлен эффектом двойного лучепреломления.
К системе дифференциальных уравнений можно добавить уравнение расчета полного омического затухания вдоль траектории [1]. Для изотропного случая это уравнение имеет следующий вид:
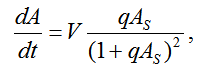
где
q = 10-6c / 2πf,
c - скорость света.
Значение омического затухания AS берется из модели поглощения КВ сигнала.
Без учета влияния магнитного поля Земли формулы упрощаются:
ε = 1 - f2N / f2,
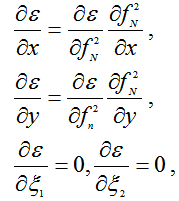
∂ε/∂f = 2f2N / f3, следовательно, M = 1.
Таким образом, имеем следующую систему дифференциальных уравнений:
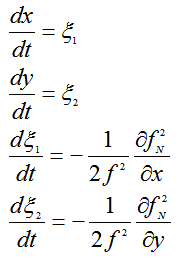
и следующие начальные значения зависимых переменных и их производных:
[x(0), y(0)] - координаты точки входа луча в ионосферу.
x'(0) = cosα,
y'(0) = sinα,
ξ1(0) = cosα,
ξ2(0) = sinα,
ξ'1(0) и ξ'2(0) – это произведение -1/2f2 и соответствующей частной производной КПЧ (∂f2/∂x или ∂f2/∂y) в точке входа луча в ионосферу.
Значения частных производных ∂f2N/∂x, ∂f2N/∂y в текущей точке определяются с помощью линейной интерполяции значений частных производных КПЧ в узловых точках модели ионосферы.
Расчеты выполняются в СКЗ.
Входные данные вводятся из текстового файла c:\cch\npt.txt:
* Файл входных данных
* Углы задаются в градусах
1) Географические координаты (широта и долгота) источника - srcGCrds
55.0 37.0
2) Географические координаты (широта и долгота) приемника - rcvrGCrds
54.0 20.0
3) Диапазон углов зондирования prbNglsNtrvl (углы задаются в градусах)
9.0 30.0
4) Шаг по углу зондирования prbNglStp (в градусах)
2.0
5) Начальная частота зондирования prbFrqncNtl (значение из диапазона 1...10 мГц)
4.0
6) Шаг по частоте зондирования prbFrqncStp, мГц
1.0
7) Допустимое отклонение луча от приемника bmRcvrDstncDvtn, км
1.0
8) Высота источника над уровнем моря hS (км)
0.0
9) Высота приемника над уровнем моря hP (км)
0.0
10) Начальная высота ионосферы над уровнем моря h0 (км)
90.0
11) Высота слоя с максимальным значением квадрата плазменной частоты hM (км)
140.0
12) Число узловых точек по углу nNgl
20
13) Число узловых точек по высоте nH
250
14) Критическая частота f2Crtcl (мГц)
4.0
15) Начало и конец интегрирования, tStrtNd
0.0 1000.0
16) Выполнить проверочную печать скалярных данных, chckDt
.T.
17) Выполнить проверочную печать частных производных КПЧ, chckDF2NDXY
.F.
18) Выполнить проверочную печать массивов, chckRrs
.F.
19) Полное имя файла с найденными решениями, fRsltsNm
c:\cch\cchRslts.txt
Кроме того, создаются массивы arrF2N, arrXY и arrDF2DXY - соответственно массив КПЧ в узловых точках, массив координат узловых точек в СКЗ и массив частных производных КПЧ в узловых точках.
В режиме тестирования для генерации массива arrF2N используется параболическая модель ионосферы.
Переменные, хранящие входные данные, объявлены в модуле commonParams.
!
! Ввод входных данных
subroutine gtNtlDt()
use commonParams
implicit none
character(1) c
open(1, file = fNptDtNm)
read(1, *) c
read(1, *) c
! Географические координаты (широта и долгота) источника
read(1, *) c
read(1, *) srcGCrds
! Географические координаты (широта и долгота) приемника
read(1, *) c
read(1, *) rcvrGCrds
! Диапазон углов зондирования (в градусах)
read(1, *) c
read(1, *) prbNglsNtrvl
! Шаг по углу зондирования (в градусах)
read(1, *) c
read(1, *) prbNglStp
! Начальная частота зондирования, мГц
read(1, *) c
read(1, *) prbFrqncNtl
! Шаг по частоте зондирования, мГц
read(1, *) c
read(1, *) prbFrqncStp
! Допустимое отклонение луча от приемника, км
read(1, *) c
read(1, *) bmRcvrDstncDvtn
! Высота источника над уровнем моря, км
read(1, *) c
read(1, *) hS
! Высота приемника над уровнем моря, км
read(1, *) c
read(1, *) hP
! Начальная высота ионосферы над уровнем моря, км
read(1, *) c
read(1, *) h0
! Высота слоя с максимальным значением квадрата плазменной частоты, км
read(1, *) c
read(1, *) hM
! Число узловых точек по углу
read(1, *) c
read(1, *) nNgl
! Число узловых точек по высоте
read(1, *) c
read(1, *) nH
! Критическая частота, мГц
read(1, *) c
read(1, *) f2Crtcl
! Начало и конец интегрирования
read(1, *) c
read(1, *) tStrtNd
! Флаг проверочной печати скалярных данных
read(1, *) c
read(1, *) chckDt
! Флаг проверочной печати частных производных КПЧ
read(1, *) c
read(1, *) chckDF2NDXY
! Флаг проверочной печати массивов
read(1, *) c
read(1, *) chckRrs
! Имя файла с найденными решениями
read(1, *) c
read(1, *) fRsltsNm
close(1)
fRsltsNm= trim(fRsltsNm)
! Открываем файл для записи найденных решений
open(2, file = fRsltsNm)
! Вывод заголовка в фале с решениями
write(2, *) 'Angle Frequency Group path Deviation'
! Число π
pi = 2.0_8 * asin(1.0_8)
! Начинаем с критической частоты, если prbFrqncNtl = 0
if (prbFrqncNtl == 0.0_8) prbFrqncNtl = f2Crtcl
end subroutine gtNtlDt
В режиме тестирования перед решением задачи Коши вызывается процедура shwNtlDt печати входных и начальных данных.
!
! Печать входных данных
subroutine shwNtlDt
use commonParams
implicit none
! Имя файла с входными данными
print '(a11, a20)', 'fNptDtNm = ', fNptDtNm
! Имя файла с найденными решениями
print '(a10, a120)', 'fRsltsNm = ', fRsltsNm
! Радиус Земли, км
print '(a7, f10.2)', 'rRth = ', rRth
! Скорость света в вакууме, км/с
print '(a10, f15.3)', 'lghtSpd = ', lghtSpd
! Число π
print '(a5, f10.2)', 'pi = ', pi
!
! Географические координаты источника и приемника (в градусах)
print '(a11, 2f10.2)', 'srcGCrds = ', srcGCrds
print '(a12, 2f10.2)', 'rcvrGCrds = ', rcvrGCrds
! Диапазон углов зондирования (углы задаются в градусах)
print '(a15, 2f10.2)', 'prbNglsNtrvl = ', prbNglsNtrvl
! Шаг по углу зондирования (в градусах)
print '(a12, f10.2)', 'prbNglStp = ', prbNglStp
! Начальная частота зондирования, мГц
print '(a14, f10.2)', 'prbFrqncNtl = ', prbFrqncNtl
! Шаг по частоте зондирования, мГц
print '(a14, f10.2)', 'prbFrqncStp = ', prbFrqncStp
! Допустимое отклонение луча от приемника, км
print '(a18, f10.2)', 'bmRcvrDstncDvtn = ', bmRcvrDstncDvtn
! Высота источника и приемника над уровнем моря, км
print '(a5, f10.2)', 'hS = ', hS
print '(a5, f10.2)', 'hP = ', hP
! Начальная высота ионосферы над уровнем моря, км
print '(a5, f10.2)', 'h0 = ', h0
! Высота слоя с максимальным значением квадрата плазменной частоты, км
print '(a5, f10.2)', 'hM = ', hM
! Число узловых точек по углу и по высоте
print '(a7, i3)', 'nNgl = ', nNgl
print '(a5, i4)', 'nH = ', nH
! Критическая частота, мГц
print '(a10, f10.2)', 'f2Crtcl = ', f2Crtcl
! Начало и конец интегрирования
print '(a10, 2f10.2)', 'tStrtNd = ', tStrtNd
! Флаг проверочной печати скалярных данных
print '(a8, L5)', 'chckDt = ', chckDt
! Флаг проверочной печати частных производных КПЧ
print '(a13, L5)', 'chckDF2NDXY = ', chckDF2NDXY
! Флаг проверочной печати массивов
print '(a9, L5)', 'chckRrs = ', chckRrs
end subroutine shwNtlDt
Приводимая ниже программа, созданная в интересах отладки, позволяет проверить все используемые процедуры и функции для заданных угла и частоты зондирования.
Для получения результата используется процедура DIVMRK математической библиотеки IMSL, решающая задачу Коши
y' = f(t, y)
для обыкновенных дифференциальных уравнений с использованием методов Рунге-Кутты различных порядков точности.
!
! Тестирование процедур и функций
program cchTst
use commonParams
implicit none
! Ввод начальных данных
call gtNtlDt()
! Печать входных данных
call shwNtlDt()
! Вычисляем угол между источником и приемником, координаты приемника в СКЗ
! и расстояние по Земле между источником и приемником
call fndRcvrCrds()
! Генерируем, используя параболическую модель ионосферы,
! массив КПЧ в узловых точках отражающего слоя ионосферы
call genArrF2N()
! Заполнение массива частных производных КПЧ
call fllNArrDF2NDXY()
! Текущий угол зондирования (в градусах)
prbNgl = prbNglsNtrvl%x
! Начальные значения
! Вычисляем координаты точки входа луча в ионосферу в СКЗ, км
call fndBmNtrncCrds()
! Начальные индексы области окружения
! Те же значения должна вычислить и подпрограмма fndNtPnts
call fndNtlIJSrrnd()
! Частные производные КПЧ (dF2NDXYCrrnt) в точке входа луча в ионосферу
call fndDF2NDXYCrrnt()
! Текущая частота зондирования (в мГц)
prbFrqnc = prbFrqncNtl
! Решение задачи Коши для угла prbNgl и частоты prbFrqnc
if (.not. chckRrs) call slvCch()
end program cchTst
!
! Подпрограмма slvCch решает задачу Коши для угла prbNgl и частоты prbFrqnc
! Если cchRslt = 1 , то подпрограмма присвоит cchRslt
! 5, если найдено решение
! 6, если обнаружен недолет
! 7, если обнаружен перелет
! 8, если луч не пересекает поверхность Земли,
! Иначе chRslt остнется без изменений
subroutine slvCch()
use dfimsl
use commonParams
implicit none
external fcn
! Расстояние между приемником и точкой пересечения луча и Земли
real(8) bmRthCrssngRcvrDstnc
! Сообщение решателя задачи Коши
character(20) sRslt
! Вычисляет в СКЗ координаты пересечения луча и Земли
logical fndBmRthCrssngCrds
! Параметры процедуры DIVMRK
! Число дифференциальных уравнений
integer, parameter :: nQtns = 4
! Значения функций (зависимых переменных) и их производных
! y(1) отвечает x
! y(2) отвечает y
! y(3) отвечает ξ1
! y(4) отвечает ξ2
real(8) y(nQtns), yprime(nQtns)
integer ido
! Начало и конец интегрирования
real(8) tStrt, tNd
tStrt = tStrtNd%x
tNd = tStrtNd%y
! Коэффициент для подпрограммы fcn оценки правых частей
! системы дифференциальных уравнений
fcnCf = -1.0_8 / (2.0_8 * prbFrqnc**2)
if (chckDt) print '(a8, f10.4)', 'fcnCf = ', fcnCf
y(1) = arrBmPnts(1)%x
y(2) = arrBmPnts(1)%y
y(3) = cosD(prbNgl)
y(4) = sinD(prbNgl)
yprime(1) = cosD(prbNgl)
yprime(2) = sinD(prbNgl)
yprime(3) = fcnCf * dF2NDXYCrrnt%x
yprime(4) = fcnCf * dF2NDXYCrrnt%y
! Решаем систему дифференциальных уравнений
ido = 1
call divmrk(ido, nQtns, fcn, tStrt, tNd, y, yprime)
! Освобождаем рабочую область
ido = 3
call divmrk(ido, nQtns, fcn, tStrt, tNd, y, yprime)
if (cchRslt == 1) then
! Отраженный луч покинул ионосферу и устремился к Земле
! Ищем точку пересечения луча с Землей (crssngCrds)
if (fndBmRthCrssngCrds()) then
! Луч пересекает поверхность Земли
! Вычисляем расстояние между приемником и точкой пересечения луча и Земли
bmRthCrssngRcvrDstnc = fndBmRthCrssngRcvrDstnc()
if (bmRthCrssngRcvrDstnc < bmRcvrDstncDvtn) then
! Решение найдено
cchRslt = 5
! Рассчитываем групповой путь и выводим результат в текстовый файл
call prntRslt()
sRslt = 'SUCCESS'
else
if (crssngCrds%y > rcvrCrds%y) then
! Недолет
sRslt = 'UNDERSHOT'
cchRslt = 6
else
! Перелет
sRslt = 'SHOT OVER THE TARGET'
cchRslt = 7
end if
end if
else
! Луч не пересекает поверхность Земли
sRslt = 'NO EARTH CROSSING'
cchRslt = 8
end if
else
if (cchRslt == 2) then
sRslt = 'UPPER BORDER IS CROSSED'
else
sRslt = 'RIGHT BORDER IS CROSSED'
end if
end if
call prntScrn()
! Оставляем в массиве arrBmPnts только точку входа луча в ионосферу
nBmPnts = 1
contains
!
! Вычисляет расстояние между приемником и точкой пересечения луча и Земли
real(8) function fndBmRthCrssngRcvrDstnc()
real(8) dx, dy
dx = rcvrCrds%x - crssngCrds%x
dy = rcvrCrds%y - crssngCrds%y
fndBmRthCrssngRcvrDstnc = sqrt(dx * dx + dy * dy)
end function fndBmRthCrssngRcvrDstnc
!
! Вывод результата в текстовый файл
subroutine prntRslt()
! Полный групповой путь
real(8) grpPth, fndBmGrpPth
grpPth = fndBmGrpPth()
! Заголовок
! Angle Frequency Group path Deviation'
write(2, '(f6.1, f11.2, f12.2, f11.2)') prbNgl, prbFrqnc, grpPth, bmRthCrssngRcvrDstnc
end subroutine prntRslt
!
! Вывод на консоль информации о результате
subroutine prntScrn()
print '(a20)', sRslt
print '(a10, i6)', 'nBmPnts = ', nBmPnts
print '(a9, f9.2)', 'prbNgl = ', prbNgl
print '(a11, f9.2)', 'prbFrqnc = ', prbFrqnc
end subroutine prntScrn
end subroutine slvCch
!
! Оценка правых частей системы дифференциальных уравнений
subroutine fcn(n, t, y, yprime)
use commonParams
integer n
real(8) t, y(*), yprime(*)
! Находим индексы области окружения
call fndNtPnts()
if (cchRslt == 0) then
! Запоминаем текущие координаты луча
nBmPnts= nBmPnts + 1
arrBmPnts(nBmPnts)%x= y(1)
arrBmPnts(nBmPnts)%y= y(2)
yprime(1) = y(3)
yprime(2) = y(4)
! Находим частные производные КПЧ в текущей точке траектории луча
call fndDF2NDXYCrrnt()
yprime(3) = fcnCf * dF2NDXYCrrnt%x
yprime(4) = fcnCf * dF2NDXYCrrnt%y
else
! print '(a32, 2f10.2, 2i5)', 'Surroundings not found. h0 & hm', h0, hm, iSrrnd, jSrrnd
! print *, cchRslt, t, arrBmPnts(nBmPnts)
! Завершаем вычисления, устанавливая текущее время за пределы верхней границы
! интервала интегрирования
t = tStrtNd%y
end if
end subroutine fcn
Решением задачи прямого зондирования ионосферы являются такие значения частоты и угла зондирования, при которых сигнал, переданный источником, достигает приемника. Решение ищется в некоторых диапазонах частот и углов зондирования. При удачно выбранных диапазонах может быть найдено несколько решений. Все решения находятся по следующей схеме:
В схеме использованы два следующих обработчика.
Обработчик наращивания угла зондирования
prbNgl = prbNgl + prbNglStp.
Если prbNgl > prbNglsNtrvl%y, тогда
! Угол зондирования превысил верхнюю границу интервала зондирования
Останов.
Иначе
Перейти к п. 5 основной схемы.
Конец Если.
Конец Обработчика наращивания угла зондирования.
Обработчик Перелета
Если prbFrqnc > prbFrqncNtl, тогда
Найти решение, выбирая текущую частоту по принципу дихотомии.
Иначе
Вывести сообщение об ошибочном задании начальной частоты зондирования.
Вызвать обработчик наращивания угла зондирования.
Конец Если.
Конец Обработчика Перелета.
Поиск решения по принципу дихотомии в обработчике Перелета выполняется следующим образом. Пусть frqncA - это частота недолета, frqncB - это частота перелета:
В приведенной схеме учтено, что, во-первых, групповой путь растет при увеличении частоты зондирования, и, во-вторых, что нет смысла наращивать частоту зондирования, если луч, "пробил" верхнюю границу ионосфере, а следует перейти к следующему углу зондирования.
Приведенная схема вычислений реализуется следующим кодом:
program cch
use commonParams
implicit none
logical chckDtLd
! Ввод начальных данных
call gtNtlDt()
! Печать входных данных
call shwNtlDt()
! Вычисляем угол между источником и приемником, координаты приемника в СКЗ
! и расстояние по Земле между источником и приемником
call fndRcvrCrds()
! Генерируем, используя параболическую модель ионосферы,
! массив КПЧ в узловых точках отражающего слоя ионосферы
call genArrF2N()
! Заполнение массива частных производных КПЧ
call fllNArrDF2NDXY()
! Текущий угол зондирования (в градусах)
prbNgl = prbNglsNtrvl%x
chckDtLd = chckDt
! Цикл по углу зондирования
do while (prbNgl < prbNglsNtrvl%y)
! Восстанавливаем флаг промежуточной печати
chckDt = chckDtLd
! Начальные значения
! Вычисляем координаты точки входа луча в ионосферу в СКЗ, км
call fndBmNtrncCrds()
! Начальные индексы области окружения
! Те же значения должна вычислить и подпрограмма fndNtPnts
call fndNtlIJSrrnd()
! Частные производные КПЧ (dF2NDXYCrrnt) в точке входа луча в ионосферу
call fndDF2NDXYCrrnt()
! Отменяем промежуточную печать
chckDt = .false.
! Цикл по частоте зондирования
! Текущая частота зондирования (в мГц)
prbFrqnc = prbFrqncNtl
do while (.true.)
! Решение задачи Коши для угла prbNgl и частоты prbFrqnc
call slvCch()
if (cchRslt == 2 .or. cchRslt == 5) then
call prbNglNcrmnttn()
exit
else if (cchRslt == 6) then
! Недолет
prbFrqnc = prbFrqnc + prbFrqncStp
else if (cchRslt == 7 .or. cchRslt == 8) then
! Перелет
call shtVrTrtmnt()
exit
end if
end do
end do
contains
!
! Обработчик наращивания угла зондирования
subroutine prbNglNcrmnttn()
prbNgl = prbNgl + prbNglStp
! Угол зондирования превысил верхнюю границу интервала зондирования
if (prbNgl > prbNglsNtrvl%y) stop
end subroutine prbNglNcrmnttn
!
! Обработчик Перелета
subroutine shtVrTrtmnt()
real(8) frqncA, frqncB
if (prbFrqnc > prbFrqncNtl) then
! Дихотомия
print '(/a26, f9.2)', 'DICHOTOMY START. PrbNgl = ', prbNgl
frqncA = prbFrqnc - prbFrqncStp
frqncB = prbFrqnc
do while (frqncB - frqncA > 0.1_8)
prbFrqnc = (frqncA + frqncB) / 2.0_8
call slvCch()
if (cchRslt == 5) then
! Найдено решение
! Формирование текстовых файлов с данными для графического вывода
! call mgMpGrpPthDt()
exit
else if (cchRslt == 6) then
! Недолет
frqncA = prbFrqnc
else if (cchRslt == 7) then
! Перелет
frqncB = prbFrqnc
else
print *, 'DICHOTOMY ERROR'
exit
end if
end do
else
print '(a45, f9.2)', 'Invalid initial frequency value. PrbNgl = ', prbNgl
end if
! Увеличиваем угол зондирования
call prbNglNcrmnttn()
end subroutine shtVrTrtmnt
!
! Выводит данные, необходимые для отображения группового пути
! и градиентной заливки ионосферы зондируемой области ионосферы
subroutine mgMpGrpPthDt()
integer i, j
! Файл с параметрами сигнала и координатами узловых точек
open(21, file = 'ntPntsXY.txt')
! Угол и частота зондирования и угол между источником и приемником
write(21, '(2f15.2)') prbNgl, prbFrqnc, 180.0_8 * srcRcvrNgl / pi
! Число точек по углу и высоте
write(21, '(2i5)') nNgl, nH
! Массив с координатами узловых точек
write(21, '(2f15.2)') arrXY
! Файл со значениями КПЧ в узловых точках
open(22, file = 'ntPntsF2N.txt')
write(22, '(f15.2)') arrF2N
! Файл со значениями координат точки P3 пересечения луча и Земли
! и координат точек на траектории луча в ионосфере
open(23, file = 'p3Crdnts.txt')
write(23, '(2f15.2)') crssngCrds
! Число точек на траектории луча в ионосфере
write(23, '(i8)') nBmPntsTKp
! Точки траектории луча в ионосфере
write(23, '(2f15.2)') arrBmPnts(1:nBmPntsTKp)
end subroutine mgMpGrpPthDt
end program cch
Пример реализации дихотомии можно наблюдать на рис. 10.
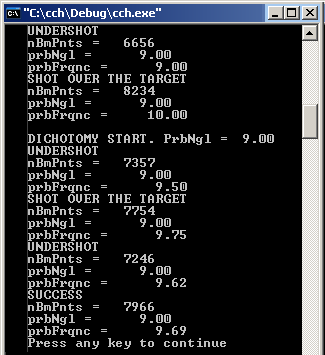
Рис. 10. Четыре шага дихотомии
Найденное решение выведено в файл с результатами (рис. 11).
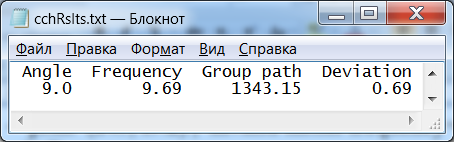
Рис. 11. Решение, найденное при реализации дихотомии
Приведено решение упрощенной задачи определения параметров декаметрового сигнала, зондируещего ионосфеу. Для отладки и тестирования программы использована параболическая модель ионосферы.
Практическую ценность приложение приобретет в случае удачных испытаний на реальных данных, например IRI [2], и учета влияния на зондирующий КВ-сигнал магнитного поля Земли и омического затухания.
Данные, используемы различными процедурами, собраны в модуле commonParams.
module commonParams
type pnt
real(8) x, y
end type pnt
!
! Константы
! Имя файла входных данных
character(*), parameter :: fNptDtNm = 'c:\cch\npt.txt'
! Радиус Земли, км
real(8), parameter :: rRth = 6370.0_8
! Скорость света в вакууме, км/с
real(8), parameter :: lghtSpd = 299792.458_8
! Число π = 2.0_8 * asin(1.0_8)
real(8) :: pi
!
! Входные данные
! Географические координаты (широта и долгота) источника и приемника (в градусах)
type(pnt) srcGCrds, rcvrGCrds
! Диапазон углов зондирования (в градусах)
type(pnt) prbNglsNtrvl
! Шаг по углу зондирования (в градусах)
real(8) prbNglStp
! Начальная частота зондирования, мГц. Если задан 0, то берется критическая частота
real(8) prbFrqncNtl
! Шаг по частоте зондирования, мГц
real(8) prbFrqncStp
! Допустимое отклонение луча от приемника, км
real(8) bmRcvrDstncDvtn
! Высота источника и высота приемника над уровнем моря, км
real(8) hS, hP
! Начальная высота ионосферы над уровнем моря, км
real(8) h0
! Высота слоя с максимальным значением квадрата плазменной частоты, км
real(8) hM
! Число узловых точек по углу и высоте
integer nNgl, nH
! Критическая частота, мГц
real(8) f2Crtcl
! Начало и конец интегрирования
type(pnt) tStrtNd
! Флаг проверочной печати скалярных данных
logical chckDt
! Флаг проверочной печати частных производных КПЧ
logical chckDF2NDXY
! Флаг проверочной печати массивов
logical chckRrs
! Имя файла с найденными решениями
character(250) fRsltsNm
!
! Начальные, задаваемые в программе данные
! Текущий угол зондирования (в градусах)
real(8) prbNgl
! Текущая частота зондирования (в мГц)
real(8) prbFrqnc
!
! Массивы
! Массив КПЧ в узловых точках отражающего слоя ионосферы
! f2N = arrF2N(i, j), где i = 1:nNgl, j = 1:nH
real(8), allocatable :: arrF2N(:, :)
! Массив координат узловых точек в СКЗ, км
type(pnt), allocatable :: arrXY(:, :)
! Массив частных производных КПЧ в узловых точках
type(pnt), allocatable :: arrDF2NDXY(:, :)
! Массив точек траектории луча в ионосфере
type(pnt) arrBmPnts(100000)
! Число точек на траектории луча в ионосфере
integer :: nBmPnts = 0, nBmPntsTKp
!
! Вычисляемые значения
! Координаты приемника в СКЗ, км
type(pnt) rcvrCrds
! Угол между источником и приемником (в радианах)
real(8) srcRcvrNgl
! Расстояние по Земле между источником и приемником, км
real(8) srcRcvrErthDstnc
! Координаты в СКЗ точки пересечения луча и Земли, км
type(pnt) crssngCrds
! Полный групповой путь, км
real(8) grpPth
! Индексы области окружения текущей точки траектории луча
integer iSrrnd, jSrrnd
! Значения частных производных КПЧ в текущей точке траектории луча
type(pnt) dF2NDXYCrrnt
! шаг между узловыми точками по углу и высоте
real(8) sNgl, sH
! Коэффициент для подпрограммы fcn оценки правых частей
! системы дифференциальных уравнений
real(8) fcnCf
! Результат решения задачи Коши
! 0, если луч находится в исследуемой области ионосферы
! 1, если отраженный луч покинул ионосферу
! 2, если луч пробил верхнюю границу ионосферы
! 3, если луч пробил правую границу (prbNglsNtrvl%y) исследуемой области ионосферы
! 5, если найдено решение
! 6, если обнаружен недолет
! 7, если обнаружен перелет
! 8, если луч не пересекает поверхность Земли
integer cchRslt
end module commonParams
--
-- Вывод рис. 1
-- Траектория луча и система координат зондирования
fn addNS p p2 clr crn dm = (
s = line pos:p wireColor:clr render_displayRenderMesh:dm
addNewSpline s
if crn then (
addKnot s 1 #corner #line p
addKnot s 1 #corner #line p2
)
else (
addKnot s 1 #smooth #curve p
addKnot s 1 #smooth #curve ((p + p2) * 0.625 )
addKnot s 1 #smooth #curve p2
)
updateShape s
)
delete $*
r = 200
th = 16
h = 30
rh = r + h
tm = matrix3 [1,0,0] [0,0,1] [0,-1,0] [0, 0, 0]
clr = black
clr2 = red
p0 = [0, 0, 0]
xs = 200
zs = 173
x1 = 148
z1 = 217
a = arc radius:r from:0 to:100 transform:tm rotation:(quat 0.67 -0.22 0.22 0.67) wireColor:clr
scale a [2, 1, 1]
a2 = arc radius:rh from:0 to:110 transform:tm rotation:(quat 0.67 -0.22 0.22 0.67) wireColor:clr
scale a2 [2, 1, 1]
sphere radius:2 pos:[-xs, 0, zs] wireColor:clr2
sphere radius:2 pos:[xs, 0, zs] wireColor:clr2
sphere radius:2 pos:[-x1, 0, z1] wireColor:clr2
sphere radius:2 pos:[x1, 0, z1] wireColor:clr2
dx = 150
dz = 100
addNS [-xs, 0, zs] [-x1, 0, z1] clr true on
addNS [x1, 0, z1] [xs, 0, zs] clr true on
addNS [-x1, 0, z1] [x1, 0, z1] clr false on
addNS [-xs, 0, zs] [131, 0, 275] clr true off
addNS [-xs, 0, zs] [-232, 0, 273.5] clr true off
addNS [0, 0, zs - 75] [0, 0, rh] clr true off
addNS [0, 0, r] [-4, 0, r - 8] clr true off
addNS [0, 0, r] [4, 0, r - 8] clr true off
text size:th transform:tm pos:[0.75 * th, 0, zs - 1.5 * th] text:"R" wireColor:clr
text size:th transform:tm pos:[0.75 * th, 0, r + 0.35 * h] text:"ho" wireColor:clr
text size:th transform:tm pos:[112.5, 0, 274] text:"x" wireColor:clr
text size:th transform:tm pos:[-220, 0, 265] text:"y" wireColor:clr
text size:th transform:tm pos:[-xs, 0, zs - 1.25 * th] text:"P0" wireColor:clr
text size:th transform:tm pos:[xs, 0, zs - 1.25 * th] text:"P3" wireColor:clr
text size:th transform:tm pos:[-x1, 0, z1 + 0.75 * th] text:"P1" wireColor:clr
text size:th transform:tm pos:[x1, 0, z1 + 0.75 * th] text:"P2" wireColor:clr
arrS = for k = 1 to shapes.count collect shapes[k]
arc radius:(0.175 * r) from:19 to:40 transform:tm pos:[-xs, 0, zs] wireColor:clr
text size:th transform:tm pos:[-162, 0, 190] text:"a" wireColor:clr font:"Symbol"
select $*
max tool zoomExtents
clearSelection()
В принципе задача может решаться и в иной, например в приведенной на рис. П1, системе координат.
Рис. П1. Альтернативная система координат решения задачи Коши прямого зондирования ионосферы
Для вывода рис. П1 употреблен следующий код:
--
-- Вывод рис. П1
fn addNS p p2 clr crn = (
s = line pos:p wireColor:clr
addNewSpline s
if crn then (
addKnot s 1 #corner #line p
addKnot s 1 #corner #line p2
)
else (
addKnot s 1 #smooth #curve p
addKnot s 1 #smooth #curve ((p + p2) * 0.625 )
addKnot s 1 #smooth #curve p2
)
updateShape s
)
delete $*
r = 200
th = 16
h = 30
rh = r + h
tm = matrix3 [1,0,0] [0,0,1] [0,-1,0] [0, 0, 0]
clr = black
clr2 = red
p0 = [0, 0, 0]
xs = 200
zs = 173
x1 = 148
z1 = 217
a = arc radius:r from:0 to:100 transform:tm rotation:(quat 0.67 -0.22 0.22 0.67) wireColor:clr
scale a [2, 1, 1]
a2 = arc radius:rh from:0 to:110 transform:tm rotation:(quat 0.67 -0.22 0.22 0.67) wireColor:clr
scale a2 [2, 1, 1]
sphere radius:2 pos:[-xs, 0, zs] wireColor:clr2
sphere radius:2 pos:[xs, 0, zs] wireColor:clr2
sphere radius:2 pos:[-x1, 0, z1] wireColor:clr2
sphere radius:2 pos:[x1, 0, z1] wireColor:clr2
dx = 150
dz = 100
addNS [-xs, 0, zs] [-x1, 0, z1] clr true
addNS [x1, 0, z1] [xs, 0, zs] clr true
addNS [-x1, 0, z1] [x1, 0, z1] clr false
addNS [-xs, 0, zs] [-xs + dx, 0, zs] clr true
addNS [-xs, 0, zs] [-xs, 0, zs + dz] clr true
addNS [0, 0, zs - 75] [0, 0, rh] clr true
addNS [0, 0, r] [-4, 0, r - 8] clr true
addNS [0, 0, r] [4, 0, r - 8] clr true
text size:th transform:tm pos:[0.75 * th, 0, zs - 1.5 * th] text:"R" wireColor:clr
text size:th transform:tm pos:[0.75 * th, 0, r + 0.35 * h] text:"ho" wireColor:clr
text size:th transform:tm pos:[-xs + dx - th / 2, 0, zs + 4] text:"x" wireColor:clr
text size:th transform:tm pos:[-xs + th / 2 + 2, 0, zs + dz - th / 2 - 2] text:"y" wireColor:clr
text size:th transform:tm pos:[-xs, 0, zs - 1.25 * th] text:"P0" wireColor:clr
text size:th transform:tm pos:[xs, 0, zs - 1.25 * th] text:"P3" wireColor:clr
text size:th transform:tm pos:[-x1, 0, z1 + 0.75 * th] text:"P1" wireColor:clr
text size:th transform:tm pos:[x1, 0, z1 + 0.75 * th] text:"P2" wireColor:clr
arrS = for k = 1 to shapes.count collect shapes[k]
arrS.render_renderable = on
arrS.render_displayRenderMesh = off
select $*
max tool zoomExtents
clearSelection()
--
-- Вывод рис. 2
-- Мировая система координат
fn addNS pt0 pt pt2 clr = (
s = line pos:pt0 wireColor:clr render_displayRenderMesh:on
addNewSpline s
addKnot s 1 #corner #line pt
addKnot s 1 #corner #line pt2
updateShape s
)
delete $*
r = 40; r2 = 1; pt0 = [0, 0, 0]; th = 9; clr = black
tm = matrix3 [1,0,0] [0,0,1] [0,-1,0] [0, 0, 0]
std = standard opacity:75 diffuse:blue
meditmaterials[1] = std
sph = sphere radius:r segs:32 material:std
sphere radius:r2 segs:32 wireColor:clr
ptx = [-r - 10, 0, 0]; pty = [0, -r - 10, 0]; ptz = [0, 0, r + 10]
addNS pt0 pt0 ptx clr
addNS pt0 pt0 pty clr
addNS pt0 pt0 ptz clr
text size:th transform:tm pos:(ptx + [0, 0, 3]) text:"x" wireColor:clr
ty = text size:th pos:(pty + [0, 0, 4]) text:"y" wireColor:clr
rotate ty (eulerAngles 90 0 -90)
tz = text size:th transform:tm pos:(ptz + [5, 0, -0.75 * th]) text:"z" wireColor:clr
rotate tz (eulerAngles 0 0 -45)
--
-- Вывод рис. 4
-- Вычисление координат приемника в СКЗ
fn addNS pt0 pt pt2 clr dm = (
s = line pos:pt0 wireColor:clr render_displayRenderMesh:dm
addNewSpline s
addKnot s 1 #corner #line pt
addKnot s 1 #corner #line pt2
updateShape s
)
delete $*
r = 40; r2 = 1; pt0 = [0, 0, 0]; th = 9; clr = black
tm = matrix3 [1,0,0] [0,0,1] [0,-1,0] [0, 0, 0]
circle radius:r transform:tm render_displayRenderMesh:on wireColor:clr
pts = [-30.75, 0, 25.3]; ptp = [3.9, 0, 39.8]
text size:th transform:tm pos:[-31.36, 0, 30.31] text:"S" wireColor:clr
sphere radius:r2 segs:32 wireColor:red pos:pts
text size:th transform:tm pos:(ptp + [2, 0, 2]) text:"P" wireColor:clr
sphere radius:r2 wireColor:red pos:ptp
sphere radius:r2 wireColor:red pos:pt0
addNS pt0 pt0 pts clr on
addNS pt0 pt0 ptp clr on
ptx = [-16.73, 0, 43.27]; pty = [-40.66, 0, 33.5]
addNS pt0 pts ptx clr off
addNS pt0 pts pty clr off
addNS pt0 pt0 [14, 0, 18.5] clr off
text size:(th - 2) transform:tm pos:(ptx + [2, 0, 2]) text:"x" wireColor:clr
ty = text size:(th - 2) transform:tm pos:(pty + [-2, 0, 2]) text:"y" wireColor:clr
rotate ty (eulerAngles 0 -45 0)
arc transform:tm from:85 to:143 radius:(0.3 * r) wireColor:clr
text size:(th - 2) transform:tm pos:[-4.5, 0, 14.2] text:"a" wireColor:clr font:"Symbol"
arc transform:tm from:50 to:85 radius:(0.3 * r) pos:pt0 wireColor:clr
arc transform:tm from:50.1 to:85 radius:(0.32 * r) pos:pt0 wireColor:clr
text size:(th - 2) transform:tm pos:[6.2, 0, 15.0] text:"b" wireColor:clr font:"Symbol"
--
-- Вывод рис. 5
-- Задание узловых точек для расчета квадратов плазменной частоты
fn addNS pt0 pt pt2 clr = (
s = line pos:pt0 wireColor:clr
addNewSpline s
addKnot s 1 #corner #line pt
addKnot s 1 #corner #line pt2
updateShape s
return s
)
delete $*
r = 80
r2 = 1
h = 40
rh = r + h
nNgl = 10
-- Угол между источником и приемником
nglLL = 90
dNgl = nglLL / (nNgl - 1)
nH = 5
sH = h / (nH - 1)
tm = matrix3 [1,0,0] [0,0,1] [0,-1,0] [0, 0, 0]
clr = black
clr2 = red
pt0 = [0, 0, 0]
arc radius:r from:45 to:135 transform:tm wireColor:clr
arc radius:rh from:45 to:135 transform:tm wireColor:clr
pt2 = pt0 + [rh, 0, 0]
s = addNS pt0 pt0 pt2 clr
rotate s (eulerAngles 0 -45 0)
s = addNS pt0 pt0 pt2 clr
rotate s (eulerAngles 0 -135 0)
ngl = 90 + nglLL / 2 + dNgl
for k = 1 to nNgl do (
ngl -= dNgl
hc = r - sH
for k2 = 1 to nH do (
hc += sH
s = sphere radius:r2 pos:(pt0 + [hc, 0, 0]) wireColor:clr2
about pt0 rotate s (eulerAngles 0 -ngl 0)
if k == 3 and k2 == nH do (
addNS pt0 pt0 s.pos clr
arc radius:(0.75 * r) from:115 to:135 transform:tm wireColor:clr
text size:14 transform:tm pos:[-39, 0, 53] text:"j" font:"Symbol" wireColor:clr
)
)
)
select $*
max tool zoomExtents
clearSelection()
--
-- Вывод рис. 6
-- Вычисление КПЧ в точке P
fn addNS pt pt2 clr = (
s = line pos:[0, 0, 0] wireColor:clr
addNewSpline s
addKnot s 1 #corner #line pt
addKnot s 1 #corner #line pt2
updateShape s
)
delete $*
r = 2
th = 10
clr = black
pt1 = [-50, 0, -30]
pt2 = [-70, 0, 50]
pt3 = [50, 0, -30]
pt4 = [70, 0, 50]
pt = [30, 0, 0]
pt0 = [-90, 0, -50]
ptx = pt0 + [180, 0, 0]
pty = pt0 + [0, 0, 110]
ptPx = [pt[1], 0, pt0[3]]
ptPy = [pt0[1], 0, pt[3]]
sphere radius:r pos:pt1 wireColor:red
sphere radius:r pos:pt2 wireColor:red
sphere radius:r pos:pt3 wireColor:red
sphere radius:r pos:pt4 wireColor:red
sphere radius:r pos:pt wireColor:green
text size:th transform:tm pos:(pt1 + [th, 0, 0]) text:"P1" wireColor:clr
text size:th transform:tm pos:(pt2 + [th, 0, 0]) text:"P2" wireColor:clr
text size:th transform:tm pos:(pt3 - [th, 0, 0]) text:"P3" wireColor:clr
text size:th transform:tm pos:(pt4 - [th, 0, 0]) text:"P4" wireColor:clr
text size:th transform:tm pos:(pt + [1, 0, 5]) text:"P" wireColor:clr
addNS pt1 pt2 clr
addNS pt3 pt4 clr
addNS pt0 ptx clr
addNS pt0 pty clr
addNS pt ptPx clr
addNS pt ptPy clr
addNS pt [ptx[1], 0, pt[3]] clr
ptA = [-57.545, 0, pt0[3]]
ptB = [57.954, 0, pt0[3]]
ptA2 = [ptA[1], 0, pt[3]]
ptB2 = [ptB[1], 0, pt[3]]
addNS ptA ptA2 clr
addNS ptB ptB2 clr
addNS pt1 [pt1[1], 0, pt2[3] - 10] clr
sphere radius:r pos:ptA2 wireColor:blue
sphere radius:r pos:ptB2 wireColor:blue
text size:th transform:tm pos:(ptx + [-3, 0, 3]) text:"x" wireColor:clr
text size:th transform:tm pos:(pty + [5, 0, -5]) text:"y" wireColor:clr
text size:th transform:tm pos:(ptPx - [0, 0, th]) text:"Xp" wireColor:clr
text size:th transform:tm pos:(ptPy - [th, 0, 0]) text:"Yp" wireColor:clr
text size:th transform:tm pos:(ptA - [0, 0, th]) text:"Xa" wireColor:clr
text size:th transform:tm pos:(ptB - [0, 0, th]) text:"Xb" wireColor:clr
text size:th transform:tm pos:[ptA2[1] - 5, 0, ptA2[3] - th] text:"A" wireColor:clr
text size:th transform:tm pos:[ptB2[1] + 5, 0, ptB2[3] - th] text:"B" wireColor:clr
arc radius:(pt2[3] - pt1[3] - 30) from:90 to:105 transform:tm pos:pt1 wireColor:clr
text size:th transform:tm pos:[pt1[1] - 7, 0, pt2[3] - 27] text:"a" font:"Symbol" wireColor:clr
select $*
max tool zoomExtents
clearSelection()
--
-- Вывод рис. 7
-- Поиск индексов области окружения
fn addNS pt0 pt pt2 clr = (
s = line pos:pt0 wireColor:clr render_displayRenderMesh:off
addNewSpline s
addKnot s 1 #corner #line pt
addKnot s 1 #corner #line pt2
updateShape s
return s
)
delete $*
r = 80
r2 = 1
h = 40
rh = r + h
nNgl = 10
tH = 12
-- Угол между источником и приемником
nglLL = 90
dNgl = nglLL / (nNgl - 1)
nH = 5
sH = h / (nH - 1)
tm = matrix3 [1,0,0] [0,0,1] [0,-1,0] [0, 0, 0]
clr = black
clr2 = red
pt0 = [0, 0, 0]
arc radius:r from:45 to:135 transform:tm wireColor:clr render_displayRenderMesh:off
arc radius:rh from:45 to:135 transform:tm wireColor:clr render_displayRenderMesh:off
arc radius:(0.85 * r) from:45 to:135 transform:tm wireColor:clr render_displayRenderMesh:on
pt2 = pt0 + [rh, 0, 0]
s = addNS pt0 pt0 pt2 clr
rotate s (eulerAngles 0 -45 0)
s = addNS pt0 pt0 pt2 clr
rotate s (eulerAngles 0 -135 0)
ngl = 90 + nglLL / 2 + dNgl
pt3 = [-56.569, 0, 56.569]
pt3 = [-48.083, 0, 48.083]
addNS pt0 pt3 (pt3 + [-50, 0, 50]) clr
addNS pt0 pt3 [-0.3, 0, 97.0] clr
addNS pt0 [-45.269, 0, 46.579] pt3 clr
addNS pt0 [-46.838, 0, 45.463] pt3 clr
text size:(th - 2) transform:tm pos:[-35.0, 0, 23.0] text:"R" wireColor:clr render_displayRenderMesh:off
pt4 = [-40.5, 0, 97]
addNS pt0 pt0 pt4 clr
sphere radius:r2 pos:pt4 wireColor:green
sphere radius:(r2 + 0.25) pos:[-42.263, 0, 90.37] wireColor:blue
addNS pt0 pt4 [-19.94, 0, 76.9] clr
addNS pt0 pt4 [-70.7, 0, 69.7] clr
arc radius:(0.37 * r) from:112.3 to:135 transform:tm wireColor:clr render_displayRenderMesh:off
text size:(th - 2) transform:tm pos:[-92.33, 0, 98.31] text:"y" wireColor:clr \
render_displayRenderMesh:off
text size:th transform:tm pos:[1.55, 0, 97.9] text:"x" wireColor:clr render_displayRenderMesh:off
text size:th transform:tm pos:[-20.3, 0, 28.4] text:"j" font:"Symbol" wireColor:clr \
render_displayRenderMesh:off
for k = 1 to nNgl do (
ngl -= dNgl
hc = r - sH
for k2 = 1 to nH do (
hc += sH
s = sphere radius:r2 pos:(pt0 + [hc, 0, 0]) wireColor:clr2
about pt0 rotate s (eulerAngles 0 -ngl 0)
)
)
select $*
max tool zoomExtents
clearSelection()
text size:(th - 2) transform:tm pos:[-39.3, 0, 100.22] text:"Pc" wireColor:green \
render_displayRenderMesh:on render_thickness:0.25
text size:(th - 4) transform:tm pos:[-14.6, 0, 69.6] text:"xc" wireColor:green \
render_displayRenderMesh:on render_thickness:0.25
text size:(th - 4) transform:tm pos:[-75.35, 0, 64.8] text:"yc" wireColor:green \
render_displayRenderMesh:on render_thickness:0.25
--
-- Вывод рис. 8
-- Расчет точки входа луча в ионосферу
fn addNS p p2 clr = (
s = line pos:p wireColor:clr
addNewSpline s
addKnot s 1 #corner #line p
addKnot s 1 #corner #line p2
updateShape s
)
delete $*
r = 50
th = 7
tm = matrix3 [1,0,0] [0,0,1] [0,-1,0] [0, 0, 0]
clr = black
clr2 = red
c = circle radius:r transform:tm wireColor:clr
c2 = circle radius:(r + 20) transform:tm wireColor:clr
p0 = [0, 0, 0]
p = [-31, 0, 39]
p2 = [-21, 0, 66.5]
addNS p0 p clr
addNS p [18, 0, 78] clr
addNS p [-53, 0, 66] clr
addNS p0 p2 clr
addNS p p2 clr
text size:th transform:tm pos:[-20.0, 0, 15.0] text:"R" font:"Arial" wireColor:clr
text size:th transform:tm pos:[-1, 0, 33] text:"R+ho" font:"Arial" wireColor:clr
text size:th transform:tm pos:[12, 0, 77] text:"x" font:"Arial" wireColor:clr
text size:th transform:tm pos:[-47, 0, 65] text:"y" font:"Arial" wireColor:clr
text size:th transform:tm pos:(p - [7, 0, 0]) text:"Po" font:"Arial" wireColor:clr
text size:th transform:tm pos:[-20, 0, 70] text:"Pe" font:"Arial" wireColor:clr
text size:th transform:tm pos:[5, 0, 1] text:"Pc" font:"Arial" wireColor:clr
text size:th transform:tm pos:[-29, 0, 54] text:"d" font:"Arial" wireColor:clr
arc radius:11.5 from:38 to:71 transform:tm pos:p wireColor:clr
text size:8 transform:tm pos:[-23.0, 0, 50] text:"a" font:"Symbol" wireColor:clr
sphere radius:1 pos:p wireColor:clr2
sphere radius:1 pos:p2 wireColor:clr2
arrS = for k = 1 to shapes.count collect shapes[k]
arrS.render_renderable = on
arrS.render_displayRenderMesh = off
--
-- Вывод рис. 9
-- Расчет координат [x3, y3] точки Р3 пересечения луча с поверхностью Земли
fn addNS p p2 clr crn dm = (
s = line pos:p wireColor:clr render_displayRenderMesh:dm
addNewSpline s
if crn then (
addKnot s 1 #corner #line p
addKnot s 1 #corner #line p2
)
else (
addKnot s 1 #smooth #curve p
addKnot s 1 #smooth #curve ((p + p2) * 0.625 )
addKnot s 1 #smooth #curve p2
)
updateShape s
)
delete $*
r = 200
th = 16
h = 30
rh = r + h
tm = matrix3 [1,0,0] [0,0,1] [0,-1,0] [0, 0, 0]
clr = black
clr2 = red
p0 = [0, 0, 0]
xs = 200
zs = 173
x1 = 148
z1 = 217
a = arc radius:r from:0 to:100 transform:tm rotation:(quat 0.67 -0.22 0.22 0.67) wireColor:clr
scale a [2, 1, 1]
a2 = arc radius:rh from:0 to:110 transform:tm rotation:(quat 0.67 -0.22 0.22 0.67) wireColor:clr
scale a2 [2, 1, 1]
pt2 = [x1, 0, z1]
sphere radius:2 pos:[-xs, 0, zs] wireColor:clr2
sphere radius:2 pos:[xs, 0, zs] wireColor:clr2
sphere radius:2 pos:[-x1, 0, z1] wireColor:clr2
sphere radius:2 pos:pt2 wireColor:clr2
dx = 150
dz = 100
addNS [-xs, 0, zs] [-x1, 0, z1] clr true on
addNS [x1, 0, z1] [xs, 0, zs] clr true on
addNS [-x1, 0, z1] pt2 clr false on
addNS [-xs, 0, zs] [131, 0, 275] clr true off
addNS [-xs, 0, zs] [-232, 0, 273.5] clr true off
addNS [0, 0, zs - 75] [0, 0, rh] clr true off
addNS [0, 0, r] [-4, 0, r - 8] clr true off
addNS [0, 0, r] [4, 0, r - 8] clr true off
text size:th transform:tm pos:[0.75 * th, 0, zs - 1.5 * th] text:"R" wireColor:clr
text size:th transform:tm pos:[0.75 * th, 0, r + 0.35 * h] text:"ho" wireColor:clr
text size:th transform:tm pos:[127, 0, 280] text:"x" wireColor:clr
text size:th transform:tm pos:[-220, 0, 265] text:"y" wireColor:clr
text size:th transform:tm pos:[-xs, 0, zs - 1.25 * th] text:"P0" wireColor:clr
text size:th transform:tm pos:[xs, 0, zs - 1.25 * th] text:"P3" wireColor:clr
text size:th transform:tm pos:[-x1, 0, z1 + 0.75 * th] text:"P1" wireColor:clr
text size:th transform:tm pos:[x1, 0, z1 + 0.75 * th] text:"P2" wireColor:clr
arrS = for k = 1 to shapes.count collect shapes[k]
arc radius:(0.175 * r) from:19 to:40 transform:tm pos:[-xs, 0, zs] wireColor:clr
text size:th transform:tm pos:[-162, 0, 190] text:"a" wireColor:clr font:"Symbol"
addNS pt2 [68.2, 0, 284] clr true off
arc radius:(0.075 * r) from:18 to:139 pos:[92, 0, 264] transform:tm wireColor:clr
text size:th transform:tm pos:[98, 0, 285] text:"b" wireColor:clr font:"Symbol"
select $*
max tool zoomExtents
clearSelection()
Пусть точка Р лежит в плоскости СКЗ и имеет в плоскости X0Y МСК координаты [x, y] (рис. П2).
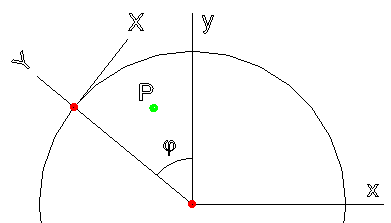
Рис. П2. К преобразованию МСК в СКЗ
Тогда координаты этой точки в СКЗ будут следующими (для совмещения СКЗ с МСК нужно повернуть по часовой стрелке СКЗ вокруг центра МСК на угол φ (φ > 0) и сместить центр СКЗ по оси y МСК на -R - hs):
X = xcosφ + ysinφ
Y = -xsinφ + ycosφ - (R + hs),
где
φ - угол между y-осями МСК и СКЗ;
R - радиус Земли;
hs - высота источника над уровнем моря.
--
-- Вывод рис. П2
fn addNS pt0 pt pt2 clr dm = (
s = line pos:pt0 wireColor:clr render_displayRenderMesh:dm
addNewSpline s
addKnot s 1 #corner #line pt
addKnot s 1 #corner #line pt2
updateShape s
)
delete $*
r = 40; r2 = 1; pt0 = [0, 0, 0]; th = 7; clr = black
tm = matrix3 [1,0,0] [0,0,1] [0,-1,0] [0, 0, 0]
circle radius:r transform:tm render_displayRenderMesh:off wireColor:clr
pts = [-30.75, 0, 25.3]; pty = [0, 0, r + 10]; ptx = [r + 10, 0, 0]
addNS pt0 pt0 ptx clr off
addNS pt0 pt0 pty clr off
text size:th transform:tm pos:(ptx + [-3, 0, 2]) text:"x" wireColor:clr
text size:th transform:tm pos:(pty + [4, 0, -4]) text:"y" wireColor:clr
sphere radius:r2 wireColor:red pos:pt0
sphere radius:r2 wireColor:red pos:pts
addNS pt0 pt0 pts clr off
ptxS = [-16.73, 0, 43.27]; ptyS = [-40.66, 0, 33.5]
addNS pt0 pts ptxS clr off
addNS pt0 pts ptyS clr off
text size:th transform:tm pos:(ptxS + [2, 0, 2]) text:"X" wireColor:clr
ty = text size:th transform:tm pos:(ptyS + [-2, 0, 2]) text:"Y" wireColor:clr
rotate ty (eulerAngles 0 -45 0)
arc transform:tm from:90 to:140 radius:(0.3 * r) wireColor:clr
text size:th transform:tm pos:[-6.0, 0, 14.0] text:"j" wireColor:clr font:"Symbol"
ptp = [-10, 0, 25]
sphere radius:r2 wireColor:green pos:ptp
text size:th transform:tm pos:(ptp + [-2.0, 0, 2.0]) text:"P" wireColor:clr