Гальваническое покрытие – это металлическая пленка, наносимая на поверхность изделий в результате электролитического процесса для придания им специальных физических и химических свойств (твердости, износостойкости, антикоррозийных, антифрикционных свойств и пр.). Сам же электролитический процесс протекает в растворе или расплаве электролита, при пропускании через него электрического тока.
Для некоторых видов гальванических ванн толщина d гальванического покрытия в зависимости от продолжительности t электролитического процесса может быть определена в результате решения следующего дифференциального уравнения:
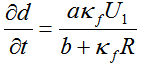
где
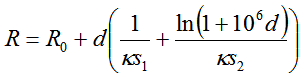
Коэффициенты приведенного уравнения определяются экспериментально.
В работе приводятся два решения уравнения:
Язык программирования - Фортран. Среда разработки - Compaq Visual Foftran 6.6. Для вывода графика функции d = f(t) использована графическая библиотека OpenGL.
Метода Рунге-Кутта 4-го порядка для решения обыкновенного дифференциального уравнения первого порядка вида y' =f (x, y) с начальным условием y(x0) = y0 реализуется следующим алгоритмом:
Подпрограмма IVMRK математической библиотеки IMSL предназначена для решения системы обыкновенных дифференциальных уравнений первого порядка (решает задачу Коши). Применяется для нежестких систем, требующих умеренной точности. Использует методы Рунге-Кутты различных порядков точности. Имеет вызов (для расчета с двойной точностью вызывается подпрограмма DIVMRK).
CALL IVMRK(ido, n, fcn, t, tend, y, yprime)
Параметры подпрограммы IVMRK (DIVMRK):
Пользовательская подпрограмма: fcn.
Входные: n, tend.
Входные/выходные: ido, t, y, yprime.
ido - флаг, характеризующий стадию вычислений. Принимает следующие значения:
Обычно первый вызов выполняется с ido = 1. При этом автоматически выделяется память - рабочая область. Затем подпрограмма устанавливает ido = 2, и это значение используется для всех повторных вызовов, кроме последнего, который выполняется с ido = 3. Последний вызов с ido = 3 освобождает рабочую область. Интегрирование на последнем шаге не выполняется.
n - число дифференциальных уравнений.
fcn - пользовательская подпрограмма, выполняющая оценку функций. Должна быть снабжена атрибутом EXTERNAL. Имеет вызов:
CALL fcn(n, t, y, yprime)
t - независимая переменная. На входе содержит начальное значение. На выходе, если не произошло ошибки, замещается на tend.
tend - значение t, в котором надо получить решение. Причем tend может быть меньше начального значения t.
y - вектор размера n зависимых переменных (значений функций). На входе y содержит начальные значения, на выходе - приблизительное решение.
yprime - массив размера n, содержащий значения y', вычисленные для (t, y).
Автоматически для решения предоставляется память:
Память можно выделить явно, применив I2MRK (DI2MRK):
CALL I2MRK(ido, n, fcn, t, tend, y, yprime, tol, thres, param, ymax, rmserr, work, Lwork)
Дополнительные параметры подпрограммы I2MRK:
Входные: thres, Lwork.
Входные/выходные: tol, param.
Выходные: ymax, rmserr.
Рабочий массив: work.
tol - допуск для контроля ошибок.
thres - вектор размера n, где thres (i) - пороговое значение для компонента решения y(i). Выбирается таким образом, что значение y(i) не существенно, когда y(i) < thres(i). Причем thres(i) ≥ SQRT(AMACH(4)).
param - вещественный массив размера 50, содержащий необязательные параметры. Если элемент param равен нулю, то для соответствующего параметра IVMRK использует установленное по умолчанию значение. Могут быть заданы следующие параметры:
По умолчанию
METHOD = 1, если 10-2 ≥ tol > 10-4;
METHOD = 2, если 10-4 ≥ tol > 10-6;
METHOD = 3, если 10-6 ≥ tol.
Следующие элементы массива param возвращаются программой:
ymax - вектор размера n, в котором ymax(i) - максимальное (на текущий момент времени) значение ABS(y(i)).
rmserr - вектор размера n, в котором rmserr(i) содержит приблизительное значение средней ошибки для решения i, i = 1, ..., n. Усреднение выполняется от точки t до текущей точки интегрирования. Значение параметра rmserr определятся, если param(3) = 1.
work - вещественный рабочий массив размера не менее 39n. Содержимое work не должно изменяться после первого вызова с ido = 1 до последнего с ido = 3.
Lwork - размер рабочего массива work.
Комментарии:
Подпрограмма IVMRK находит приблизительное решение системы дифференциальных уравнений первого порядка вида y' = f(x, y) с заданными начальными данными. При решении контролируется в соответствии с заданным допуском относительная локальная ошибка. Для повышения эффективности доступны схемы Рунге-Кутты порядков 3, 5 и 8.
Подпрограмма IVMRK основана на коде, предложенном в [1].
Пример. Решается система дифференциальных уравнений из тестового набора [2]. Используется дифференцирование назад.
y'1 = -y1 - y1y2 + k1y2, y1 (0) = 1.0;
y'2 = - k2y2 + k3 (1 - y2) y1, y2 (0) = 0.0;
k1 = 294.0, k2 = 3.0, k3 = 0.01020408, tend = 240.0.
program ivmrk
use dfimsl
integer(4), parameter :: mxparm = 50, n = 2
integer(4) :: ido, istep, lwork
real(4) :: param(mxparm), rmserr(n), t, tend, thres(n), tol, work(1000), y(n), ymax(n), yprime(n)
real(4) :: ak1 = 294.0, ak2 = 3.0, ak3 = 0.01020408
t = 0.0 ! Начальные условия
y(1) = 1.0; y(2) = 0.0
tol = 0.001 ! Допуск для оценки ошибки
thres = amach(4) ! Пороговые значения
param = 0.0 ! Действуем по умолчанию
Lwork = 1000
! Выполняем оценку производной путем дифференцирования назад
param(5) = 1
ido = 1
! Вывод заголовка таблицы результатов
write(*, "(3x, 'istep', 5x, 'time', 9x, 'y1', 10x, 'y2')")
istep = 24
do while(istep <= 240)
tend = istep
call i2mrk(ido, n, i40rk, t, tend, y, yprime, tol, thres, param, ymax, rmserr, work, Lwork)
if(ido == 5) then
! Оценка производных
yprime(1) = -y(1) - y(1) * y(2) + ak1 * y(2)
yprime(2) = -ak2 * y(2) + ak3 * (1.0 - y(2)) * y(1)
else if(istep <= 240) then
! Интегрируем в 10 равномерно расположенных точках
write(*, '(i6, 3f12.3)') istep / 24, t, y
istep = istep + 24
end if
end do
! Выводим число оценок производной
write(*, "(/, 4x, 'Number of derivative evaluations with DIVMRK =', f6.0)") param(33)
end program ivmrk
Результат:
| istep | time | y1 | y2 |
|---|---|---|---|
| 1 | 24.000 | 0.688 | 0.002 |
| 2 | 48.000 | 0.634 | 0.002 |
| 3 | 72.000 | 0.589 | 0.002 |
| 4 | 96.000 | 0.549 | 0.002 |
| 5 | 120.000 | 0.514 | 0.002 |
| 6 | 144.000 | 0.484 | 0.002 |
| 7 | 168.000 | 0.457 | 0.002 |
| 8 | 192.000 | 0.433 | 0.001 |
| 9 | 216.000 | 0.411 | 0.001 |
| 10 | 240.000 | 0.391 | 0.001 |
Number of derivative evaluations with DIVMRK = 1387
Более полное описание библиотеки IMSL см. в [3].
Приводимые процедуры воспроизводят одномерный массив в виде графика y = f(x) в декартовой системе координат. Fortran-программу вывода нескольких графиков функций на плоскости и построения поверхности z = f(x, y) можно найти в [3]. Процедуры OpenGL и порядок их употребления в Фортране описаны в [4].
Создаваемое кодом окно графического вывода может перемещаться и масштабироваться привычными способами. Кроме графика, выводятся оси координат, их разметка и координатная сетка.
module figures ! Модуль, задающий цифры, точку, знаки + и - и буквы x, y, z и e
use opengl
integer(4), parameter :: mli = 18, nli = 8
! mli - число символов (битовых образов) в массиве rasterfont
! nli - размер знакоместа
integer(1), dimension(nli) :: letter ! Массив для одного символа
integer(1) :: pointplace = 12 ! Позиция точки в массиве
! Точка выводится более компактно. Для ее поиска применяется pointplace
! rasterfont - массив символов с ASCII-кодами цифр и букв x, y, z и e
integer(1), dimension(mli, nli) :: rasterfont = reshape((/ &
#3c, #66, #c3, #c3, #c3, #c3, #66, #3c, & ! 0 (48)
#7e, #18, #18, #18, #18, #78, #38, #18, & ! 1 (49)
#ff, #60, #30, #18, #0c, #06, #e7, #7e, & ! 2 ...
#7e, #e7, #03, #03, #3e, #03, #e7, #7e, & ! 3
#0c, #0c, #0c, #ff, #cc, #6c, #3c, #1c, & ! 4
#7e, #c3, #03, #03, #fe, #c0, #c0, #ff, & ! 5
#7e, #c3, #c3, #c3, #fe, #c0, #c3, #7e, & ! 6
#30, #30, #30, #18, #0c, #06, #03, #ff, & ! 7
#7e, #c3, #c3, #c3, #3c, #c3, #c3, #7e, & ! 8
#7e, #e7, #03, #03, #7f, #c3, #c3, #7e, & ! 9 (57)
#00, #00, #00, #3f, #3f, #00, #00, #00, & ! - (45)
#00, #38, #38, #00, #00, #00, #00, #00, & ! . (46)
#7c, #c2, #c0, #fc, #c6, #c6, #7c, #00, & ! e (101 = 69 + 32)
#00, #18, #18, #ff, #ff, #18, #18, #00, & ! + (43)
#c6, #6c, #38, #38, #6c, #c6, #00, #00, & ! x (120)
#60, #30, #18, #1c, #36, #63, #c3, #00, & ! y (121)
#fe, #60, #30, #18, #0c, #fe, #00, #00, & ! z (122)
#00, #00, #00, #00, #00, #00, #00, #00 & ! (32)
/), shape = (/ mli, nli /), order = (/ 2, 1 /))
real(4) :: spx = 8.0, spy = 8.0 ! x и y-размеры знакоместа
contains
! Модуль figures включает процедуры:
! makeFigures - формирует списки команд вывода текста
! printString - выводит строку текста
! Создаем списки команд, используемых затем при выводе наборов символов
! Выводимый набор символов задается в виде строки, например: '0123456789xyz+-.e'
subroutine makeFigures()
integer(4) :: i, sg
! Начало координат битового образа
real(4) :: xorigx, yorigx, xorigy, yorigy
real(4) :: xorigz, yorigz
! Выравнивание по одному байту
call fglPixelStorei(gl_unpack_alignment, 1)
! Списки команд для вывода x- и y-координат
! Генерируем 2*m списков команд - по 2 списка на каждый заданный
! массивом rasterfont символ. Первый список для x-координат, второй - для y-координат
xorigx = 14.0; yorigx = 15.0
xorigy = 14.0; yorigy = 1.0
sg = 1
do i = 1, mli
letter = rasterfont(i, :)
call details(i, sg, xorigx, yorigx)
call details(i + mli, -sg, xorigy, yorigy)
end do
contains
! Внутренняя процедура подпрограммы makeFigures
! Детализирует различия в способах вывода x- и y-координат
subroutine details(k, sg, xorig, yorig)
integer(4) :: k, sg ! k - номер списка; sg = +1 или -1
real(4) :: xorig, yorig ! Начало координат битового образа
call fglNewList(k, gl_compile)
if(i == pointplace) then
! Способ вывода точки
call fglBitmap(spx, spy, xorig + sg, yorig, sg * (spx - 1.0), 0.0, loc(letter))
else
! Способ вывода x-координат, если sg = +1, и y-координат, если sg = -1
call fglBitmap(spx, spy, xorig, yorig, sg * (spx + 1.0), 0.0, loc(letter))
end if
call fglEndList( )
end subroutine details
end subroutine makeFigures
subroutine printString(s, gt) ! Вывод строки текста
character(*) s
character(1) gt ! gt = 'x' или 'y'
integer(2), dimension(len_trim(s)) :: ars
integer(2) :: lens, i, k
lens = len_trim(s)
do i = 1, lens ! Формируем массив номеров команд, которые нужно выполнить для вывода строки с текстом
k= int2(ichar(s(i:i)))
if(k > 47 .and. k < 58) then ! Цифры 0, 1, ..., 9
ars(i) = k - 47
else if(k == 45 .or. k == 46) then
ars(i) = k - 34 ! Знаки - и .
else if(k == 69) then ! Буква e
ars(i) = k - 56
else if(k == 43) then
ars(i) = k - 29 ! Знак +
else if(k > 119 .and. k < 123) then ! Буквы x и y
ars(i) = k - 105
else
ars(i) = 18 ! Пробел
end if
end do
if(gt == 'y') ars = ars + mli
call fglPushAttrib(gl_list_bit) ! Сохраняем атрибуты изображения
! Номер выполняемой команды будет равен ars(i)
call fglCallLists(lens, gl_short, loc(ars))
call fglPopAttrib( ) ! Восстанавливаем атрибуты изображения
end subroutine printString
end module figures
module points
use figures ! Содержит ссылку на модуль opengl.mod
! Число используемых для вывода графика точек
integer(4) :: npox, npoy
logical(4) :: gridval ! gridval = .TRUE., если сетка отображается
real(4) :: gridx, gridy ! Шаги координатной сетки по осям x и y
logical(4) :: coordval ! coordval = .TRUE., если выводятся координаты
! Число шагов координатной сетки по осям x и y
integer(4), parameter :: ngx = 5, ngy = ngx
! px, py - массивы, задающие выводимый график
real(4), allocatable, dimension(:) :: px, py
real(4), allocatable, dimension(:, :, :) :: sn
real(4) :: xl, xr, yb, yt ! Протяженность осей координат
real(4) :: cols(3) ! Массив цветов для графиков функций
real(4) :: xmi1, xma1, ymi1, yma1
logical(4) :: fzer = .true. ! fzer = .FALSE., когда 0.0 не выводится по оси y
! Образец для вывода координатной сетки (пунктир)
integer(2) :: pattern = 2#0011001100110011
contains
! Модуль points содержит процедуры:
! initGL - выполняет инициализацию окна OpenGL
! setVars - вычисляет протяженность осей координат и шаги координатной сетки
! fgrid - находит шаг координатной сетки и область ее отображения по оси x или y
! gridt - подпрограмма, выводящая линии координатной сетки и их координаты
subroutine initGL() ! Инициализация окна OpenGL
! w, h - начальные размеры окна вывода
integer(4) :: result = 0, w = 400, h = 400
character(50) :: title
call fauxInitDisplayMode(aux_single .or. aux_rgb)
call fauxInitPosition(100, 50, w, h)
title = 'График функции y = f(x)' // char(0)
call fglShadeModel(gl_flat) ! Вывод без интерполяции цветов
result = fauxInitWindow(title)
end subroutine initGL
subroutine setVars(xmi, xma, ymi, yma)
real(4) :: xmi, xma, ymi, yma
real(4) :: addx, addy, rk
! Вычисляем gridx и gridy - шаги координатной сетки по осям x и y
xmi1 = xmi; xma1 = xma; ymi1 = ymi; yma1 = yma
gridx = fgrid(xmi1, xma1, ngx)
! xmi1, xma1 - область отображения координатной сетки по оси x
gridy = fgrid(ymi1, yma1, ngy)
! Координаты xmi1, xma1, ymi1, yma1 задают границы координатной сетки
! Координаты xl, xr, yb, yt используем для задания области вывода
rk = 0.1
addx = rk * (xma1 - xmi1) ! Увеличиваем протяженность осей координат x и y соответственно на 2 * addx и 2 * addy
addy = rk * (yma1 - ymi1)
xl = xmi1 - 1.4 * addx; xr = xma1 + 0.6 * addx
yb = ymi1 - 1.2 * addy; yt = yma1 + 0.8 * addy
end subroutine setVars
! fgrid - функция модуля points; содержит функцию tita, возвращающую границу области отображения координатной сетки
function fgrid(ti, ta, ng) ! Находит шаг координатной сетки и область ее отображения по оси x или y
real(4) :: fgrid, ti, ta
integer(4) ng, k
fgrid = (ta - ti) / float(ng)
k = 0
if(fgrid < 1.0) then
do while(fgrid <= 1.0)
k = k + 1
fgrid = fgrid * 10.0
end do
fgrid = aint(fgrid) / float(10 ** k)
else if(fgrid > 10.0) then
do while(fgrid > 10.0)
k = k + 1
fgrid = fgrid / 10.0
end do
fgrid = aint(fgrid) * float(10 ** k)
else
fgrid = aint(fgrid)
end if
ti = tita(ti, 1) ! ti, ta - границы области отображения координатной сетки
ta = tita(ta, 2)
contains
function tita(t, k) ! ti и ta должны быть кратны fgrid
real(4) :: tita, t ! t - граница области отображения сетки
integer(4) :: k ! k = 1, если рассматривается ti; k = 2, если - ta
tita = 0.0
if(t < 0.0) then
do while(tita > t)
tita = tita - fgrid
end do
if(k == 2) tita = tita + fgrid
else
do while(tita < t)
tita = tita + fgrid
end do
if(k == 1) tita = tita - fgrid
end if
end function tita
end function fgrid
! Подпрограмма, выводящая линии координатной сетки и их координаты
! Содержит процедуры:
! fgs - находит шаг координатной сетки в оконных координатах
! outString - формирует строку strin, которая содержит координаты выводимой линии
! makeStrin - формирует строку, которая используется для вывода координат сетки
subroutine gridt(ti1, ta1, ti2, ta2, ti3, ta3, gt, grid)
real(4) :: ti1, ta1, ti2, ta2, ti3, ta3 ! Протяженность осей координат
character(1) :: gt ! Вид линий: 'x' или 'y'
! strin - строка, содержащая координату линии координатной сетки
character(10) :: strin
! grid - шаг координатной сетки
real(4) :: t, pt1(3), pt2(3), grid
logical(4) :: fl
integer(4) :: gs ! Шаг сетки в оконных координатах
integer(4) :: tcur, tlast ! tlast - координата последнего вывода текста
! Применяется для предотвращения наложения строк, содержащих координаты сетки
! Перекрытие строк может возникнуть при незначительной ширине (высоте) окна вывода
gs = fgs( )
tlast = 0
tcur = 0 ! Текущая позиция вывода текста
! Находим положение первой выводимой линии координатной сетки
t = ti1 - grid
do while(t < ta1) ! Вывод линий координатной сетки
fl = .true. ! Истина, если линии выводятся
t = t + grid ! Если gt = 'x', то выводятся x-линии
if(abs(t) < 0.9 * grid) fl = .false.
if(gt == 'x') then
pt1 = (/ t, ti2, ti3 /)
pt2 = (/ t, ta2, ti3 /)
else if(gt == 'y') then
pt1 = (/ ti2, t, ti3 /)
pt2 = (/ ta2, t, ti3 /)
end if
if(coordval) call outString( ) ! Вывод координат или имени оси координат
if(fl) then
call fglBegin(gl_lines) ! Вывод очередной линии координатной сетки
call fglVertex3fv(loc(pt1))
call fglVertex3fv(loc(pt2))
call fglEnd( )
end if
end do
contains
! fgs, outString и makeStrin - внутренние процедуры подпрограммы gridt
! fgs - находит шаг координатной сетки в оконных координатах
function fgs( )
integer(4) :: fgs, k ! k - номер измерения
real(8), dimension(4, 4) :: modelMatrix, projMatrix
integer(4), dimension(4) :: viewport
real(8) :: win1(2), win2(2), pt(4), ptn(4)
call fglGetDoublev(gl_modelview_matrix, loc(modelMatrix))
call fglGetDoublev(gl_projection_matrix, loc(projMatrix))
call fglGetIntegerv(gl_viewport, loc(viewport))
select case(gt)
case('x'); k = 1; pt = (/ ti1, ti2, ti3, 1.0 /)
case('y'); k = 2; pt = (/ ti2, ti1, ti3, 1.0 /)
end select
ptn = matmul(matmul(projMatrix, modelMatrix), pt)
win1 = (ptn(1:2) + 1.0_8) * dfloat((viewport(3:4) - viewport(1:2)) / 2)
pt(k) = pt(k) + real(grid, 8)
ptn = matmul(matmul(projMatrix, modelMatrix), pt)
win2 = (ptn(1:2) + 1.0_8) * dfloat((viewport(3:4) - viewport(1:2)) / 2)
win1 = win2 - win1
fgs = int(sqrt(sum(win1 * win1)))
end function fgs
! outString - внутренняя процедура подпрограммы gridt
subroutine outString( ) ! Формирует и выводит строку с текстом
integer(4) :: slen ! Длина строки с выводимым текстом
! Формируем строку strin, которая содержит координаты выводимой линии
if(abs(t) > 0.1 * grid) then
call makeStrin(strin, t, gt)
else ! Выводится координата 0.0
strin = '0.0'
end if
tcur = tcur + gs ! Текущая позиция вывода текста
! Если не нужен вывод 0.0 по оси y
if(.not. fzer .and. gt == 'y' .and. strin == '0.0') return
if(tlast > 0) then ! Если выводится не первая координата
slen = len_trim(strin) ! Проверим, можно ли разместить новый текст
if(gt == 'x') then
if(tcur - 2 * slen * spx < tlast) return
else ! gt = 'y'
if(tcur - 3 * spy < tlast) return
end if
end if
tlast = tcur ! Текст можно разместить без перекрытий
! Вывод сформированной строки strin
! Растровая позиция первой цифры строки strin
call fglRasterPos2fv(loc(pt1))
! Вывод координат
call printString(trim(strin), gt)
end subroutine outString
! makeStrin - внутренняя процедура подпрограммы gridt
subroutine makeStrin(strin, t, gt) ! Формирует строку, которая используется для вывода координат сетки
character(*) strin, gt
real(4) :: t
! Максимальное число позиций для координат - 5; минимальное - 3
real(4) :: ctpmin = 0.0099, ctmmax = -0.099
! Если 0.0010 <= t <= 9999., то используется формат F
! Если -999. <= t <= -0.010, то также используется формат F
! Если 9999. < t <= .9e+9), используется формат E5.1e1
! Если t = 0, то возвращается '0.0'
! Во всех остальных случаях возвращается пробел
integer(4), parameter :: np= 7, nm = 5
integer(4) :: k, i, j ! Номер выбранного в массиве fmt формата
character(1) :: ch
character(10), dimension(np) :: fmtp = (/ '(F5.4)', '(F4.3)', '(F3.2)', '(F3.1)', '(F3.0)', '(F4.0)', '(F5.0)' /)
character(10), dimension(nm) :: fmtm = (/ '(F5.3)', '(F4.2)', '(F4.1)', '(F4.0)', '(F5.0)' /)
character(10) :: fmt
fmt = ' '
if(t >= 0.00095 .and. t < 10000. .or. t >= -999. .and. t <= -0.0095) then
k = 1
if(t > 0) then
! (Минимальное положительное значение) * 10 для формата F
ct = ctpmin
do while(ct <= t .and. k < np)
k = k + 1
ct = ct * 10
end do
else
! (Максимальное отрицательное значение) / 10 для формата F
ct = ctmmax
do while(ct > t .and. k < nm)
k = k + 1
ct = ct * 10
end do
end if
! if(t >= 0.0010 .and. t < 0.0100) fmt = '(F5.4)'
! if(t >= 0.010 .and. t < 0.100) fmt = '(F4.3)'
! if(t >= 0.10 .and. t < 1.00) fmt = '(F3.2)'
! if(t >= 1.0 .and. t < 10.0) fmt = '(F3.1)'
! if(t >= 10.0 .and. t < 100.0) fmt = '(F3.0)'
! if(t >= 100.0 .and. t < 1000.0) fmt = '(F4.0)'
! if(t >= 1000.0 .and. t < 10000.0) fmt = '(F5.0)'
!
! if(t <= -0.010 .and. t > -0.100) fmt = '(F5.3)'
! if(t <= -0.10 .and. t > -1.00) fmt = '(F5.2)'
! if(t <= -1.0 .and. t > -10.0) fmt = '(F4.1)'
! if(t <= -10. .and. t > -100.) fmt = '(F4.0)'
! if(t <= -100. .and. t > -1000.) fmt = '(F5.0)'
if(t > 0) then
fmt = fmtp(k)
else
fmt = fmtm(k)
end if
else if(t > 0.0 .and. t <= .9e+9) then
fmt = '(e5.1e1)'
else if(abs(t) < tiny(t)) then
strin = '0.0'
return
else
strin = ' '
return
end if
write(strin, fmt) t ! Преобразование число - строка
! Меняем порядок следования символов в строке
if(gt == 'y') then
k = len_trim(strin)
do i = 1, k / 2
ch = strin(i:i)
j = k - i + 1
strin(i:i) = strin(j:j)
strin(j:j) = ch
end do
end if
end subroutine makeStrin
end subroutine gridt
end module points
! Содержит интерфейсы подпрограмм myReshape1 и display1. Они должны обладать атрибутом EXTENAL
module GLface
interface
subroutine myReshape1(w, h)
!ms$ attributes stdcall, alias : '_myReshape1@8' :: myReshape1
integer(4) :: w, h
end subroutine myReshape1
subroutine display1( )
!ms$ attributes stdcall, alias : '_display1@0' :: display1
end subroutine display1
end interface
end module GLface
! Модуль с интерфейсами программ вывода графика функции
module alib
! Параметры с атрибутом OPTIONAL - необязательные
interface
subroutine drawCurve(npx, xmi, xma, arrF, clr, grid, coords)
integer(4) :: npx ! Число точек, используемых для вывода кривой
real(4) :: xmi, xma ! Диапазон изменения аргумента x
real(4) :: arrF(1000)
real(4) :: clr(3)
logical(4), optional :: grid, coords ! grid = .TRUE., если сетка отображается
end subroutine drawCurve ! coords = .TRUE., когда выводятся координаты
end interface
end module alib
! Подпрограмма вывода графиков функций одной переменной
subroutine drawCurve(npx, xmi, xma, arrF, clr, grid, coords)
use msfwin
use points
use GLface ! Содержит интерфейсы myReshape1 и display1
integer(4) :: npx
real(4) :: xmi, xma, ymi, yma ! Диапазоны изменения координат
real(4) arrF(1000)
real(4) clr(3)
logical(4), optional :: grid, coords
real(4) :: x, y, dx
integer(4) :: i, j
! Число точек, используемых при выводе графика
npox = npx
cols(:) = clr ! Формируем массив цветов
gridval = .true. ! По умолчанию gridval = .TRUE.
if(present(grid)) gridval = grid ! gridval = .TRUE., если отображается сетка
coordval = gridval ! coordval = .TRUE., если выводятся координаты
if(present(coords)) coordval = coords
if(.not. allocated(px)) allocate(px(npox), py(npox))
yma = -huge(yma)
ymi = huge(ymi)
dx = (xma - xmi) / float(npox)
x = xmi
do i = 1, npox
y = arrF(i)
px(i) = x; py(i) = y
x = x + dx
yma = max(yma, y)
ymi = min(ymi, y)
end do
call initGL()
! Формирование списков команд, пригодных для вывода текста
call makeFigures()
! Вычисляем протяженность осей координат и шаги координатной сетки
call setVars(xmi, xma, ymi, yma)
! Смотрим, нужно ли выводить 0.0 по оси y (не нужно, если нижний левый угол графика - это начало координат)
if(abs(xmi1) < tiny(xmi1) .and. abs(ymi1) < tiny(ymi1)) fzer = .false.
! При изменении размеров окна вызывается подпрограмма myReshape1
call fauxReshapeFunc(loc(myReshape1))
! Подпрограмма display1 выполняет роль оконной процедуры
! Вызывается каждый раз при перемещении и изменении размеров окна вывода
! и выводит оси координат их рахметку, координатную сетку и график функции
call fauxMainLoop(loc(display1))
deallocate(px, py)
end subroutine drawCurve
subroutine myReshape1(w, h)
!ms$ attributes stdcall, alias : '_myReshape1@8' :: myReshape1
use points ! Подпрограмма, формирующая матрицу проецирования
integer(4) :: w, h
call fglViewport(0, 0, w, h) ! Задание видового порта
call fglMatrixMode(gl_projection); call fglLoadIdentity( )
call fgluOrtho2D(xl, xr, yb, yt)
end subroutine myReshape1
! Выводит оси координат их рахметку, координатную сетку и график функции
subroutine display1( ) ! Вывод изображения
!ms$ attributes stdcall, alias : '_display1@0' :: display1
use points
integer(4) :: i, j
real(4) :: cc(3)
call fglClearColor(1.0, 1.0, 1.0, 1.0) ! Цвет фона - белый
call fglClear(gl_color_buffer_bit) ! Очистка буфера цвета
call fglColor3f(0.0, 0.0, 0.0) ! Текущий цвет - черный
if(gridval) then ! Вывод координатной сетки по образцу
call fglLineStipple(2, pattern) ! Повторяем каждый бит образца 2 раза
! Теперь вывод линии будет выполняться с применением образца
call fglEnable(gl_line_stipple)
call gridt(xmi1, xma1, ymi1, yma1, 0.0, 0.0, 'x', gridx)
call gridt(ymi1, yma1, xmi1, xma1, 0.0, 0.0, 'y', gridy)
call fglDisable(gl_line_stipple)
end if
call fglBegin(gl_lines) ! Вывод осей координат
call fglVertex2f(xmi1, 0.0)
call fglVertex2f(xma1, 0.0)
call fglVertex2f(0.0, ymi1)
call fglVertex2f(0.0, yma1)
call fglEnd( )
call fglRasterPos2f(xma1, 0.0) ! Вывод имени оси x
letter = rasterfont(15, :)
call fglBitmap(spx, spy, 10.0, -4.0, 0.0, 0.0, loc(letter))
call fglRasterPos2f(0.0, yma1) ! Вывод имени оси y
letter = rasterfont(16, :)
call fglBitmap(spx, spy, -4.0, 10.0, 0.0, 0.0, loc(letter))
call fglFlush( ) ! Вывод на экран осей координат и сетки
cc = cols(:) ! cc - текущий цвет
call fglColor3fv(loc(cc))
call fglLineWidth(2.0)
call fglBegin(gl_line_strip)
do i = 1, npox
call fglVertex2f(px(i), py(i))
end do
call fglEnd( )
call fglFlush( ) ! Отображение y = f(x)> экране
end subroutine display1
Для построения графика функции (отображения одномерного массива данных) вызывается подпрограмма drawCurve. Пример употребления подпрограммы см. в следующем разделе.
Используется двойная точность, результат выводится на экран, в текстовый файл и в виде графика.
program clcD
use alib
implicit none
integer k, m
character(*), parameter :: frm = "(5x, 'Time', 9x, 'd')", frm2 = '(f12.2, e15.6)'
real(8) arrD(1000)
real(8) c1, c2, c3, c4
real(8) :: tS = 0.0_8, dS = 0.0_8, tE = 1500.0_8, h = 0.1_8, h2, t, d
real(8) fn
! Вывод заголовка таблицы результатов
open(1, file = "rslt.txt")
print frm
write(1, frm)
t = tS
d = dS
h2 = 0.5_8 * h
m = 0
k = 1
arrD(k) = d
print frm2, t, d
write(1, frm2) t, d
do while(t < tE)
c1 = h * fn(t, d)
c2 = h * fn(t + h2, d + 0.5_8 * c1)
c3 = h * fn(t + h2, d + 0.5_8 * c2)
c4 = h * fn(t + h2, d + c3)
d = d + (c1 + 2.0_8 * c2 + 2.0_8 * c3 + c4) / 6.0_8
t = t + h
m = m + 1
! Выводим каждую 500-ю точку
if(mod(m, 500) == 0) then
print frm2, t, d
write(1, frm2) t, d
k = k + 1
arrD(k) = d
end if
end do
!
call drawCurve(k, 0.0, 1550.0, real(arrD), (/ 1.0, 0.0, 0.0 /), grid = .true., coords = .true.)
end program clcD
real(8) function fn(t, d)
implicit none
real(8) t, d
real(8) r0, u0, ks1, ks2, kf, b, a, r
r0 = 0.1_8
u0 = 300.0_8
b = 1.0_8
a = 2.25e-8_8
ks1 = 2.7e-6_8
ks2 = 1.3e-6_8
kf = 0.179_8
r = r0 + d * (1.0_8 / ks1 + log(1.0_8 + 1.0e6_8 * d) / ks2)
fn = a * kf * u0 / (b + kf * r)
end function fn
Также употребляется двойная точность и вывод результата на экран, в текстовый файл и в виде графика.
program rgnMn
use dfimsl
use alib
implicit none
integer(4), parameter :: n = 1
integer(4) :: ido, iStep, iEnd, dStep, k
real(8) :: t, tEnd, y(n), yprime(n)
real(8) arrD(1000)
external :: fcn
character(*), parameter :: frm = "(5x, 'Time', 9x, 'd')", frm2 = '(f12.2, e15.6)'
! Начальные условия
t = 0.0_8
y(1) = 0.0_8
open(1, file = 'rgn.txt')
write(1, frm)
! Вывод заголовка таблицы результатов
print frm
ido = 1
iStep = 0
iEnd = 1500
dStep = 50
k = 1
arrD(k) = 0.0
do while(iStep < iEnd)
iStep = iStep + dStep
tEnd = iStep
call divmrk(ido, n, fcn, t, tend, y, yprime)
print frm2, t, y
write(1, frm2) t, y
k = k + 1
arrD(k) = y(1)
end do
ido = 3 ! Освобождаем память
call divmrk(ido, n, fcn, t, tend, y, yprime)
!
call drawCurve(k, 0.0, 1550.0, real(arrD), (/ 1.0, 0.0, 0.0 /), grid = .true., coords = .true.)
end program rgnMn
subroutine fcn(n, t, y, yprime)
implicit none
integer(4) :: n
real(8) :: t, y(n), yprime(n)
real(8) r0, u0, ks1, ks2, kf, b, a, r
r0 = 0.1_8
u0 = 300.0_8
b = 1.0_8
a = 2.25e-8_8
ks1 = 2.7e-6_8
ks2 = 1.3e-6_8
kf = 0.179_8
r = r0 + y(1) * (1.0_8 / ks1 + log(1.0_8 + 1.0e6_8 * y(1)) / ks2)
yprime(1) = a * kf * u0 / (b + kf * r)
end subroutine fcn
Оба способа решения уравнения расчета толщины гальванического покрытия дают одинаковый результат, графическое представление которого приведено на рис. 1.
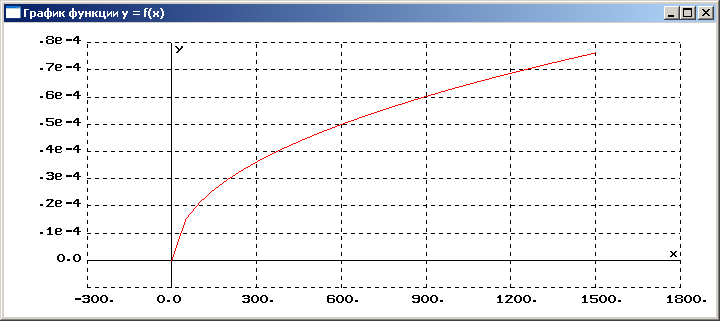
Рис. 1. Зависимость толщины гальванического покрытия от времени электролиза
Однако нелишне напомнить, что подпрограмма IVMRK математической библиотеки IMSL предоставляет гораздо более широкий спектр возможностей, чем приведенный код, реализующий метод Рунге-Кутты 4-го порядка.