Нейронная сеть применена для распознавания прописных букв русского алфавита.
Программа, реализующая алгоритм, является частью приложения, решающего задачи прогнозирования стоимости ценных бумаг. Приложение реализовано на языке FoxPro и основано на базе данных, описывающей предметную область.
Входные данные рассматриваемой задачи, как и в случае генетического алгоритма, поделены на две части. Первая часть содержит эталонные представления букв, а вторая, тестовая, – те же буквы, но с искажениями.
Эталонные буквы используются для обучения нейронной сети. Вторая часть используется для тестирования и оценки эффективности сформированной нейронной сети.
Каждая буква задается в матрице 7*8, как последовательность нулей и единиц. В наборе входных данных матрица представляется в виде последовательности ее строк. В качестве разделителя между строками использован символ *. Так, прописная буква А задается следующей строкой:
0011000*0011000*0100100*0100100*1111110*1000010*1000010*1000010
Табличное (матричное) представление этой буквы приведено на рис. 1. В пустых ячейках таблицы находятся нули.
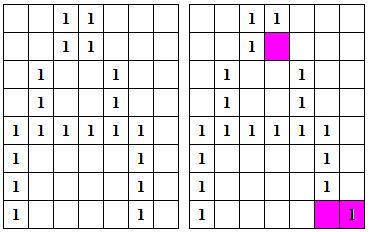
Рис. 1. Эталонное и искаженное представление буквы А
Такие буквы, как Ж, М или Ф, занимают все столбцы таблицы.
Задача состоит в том, чтобы, зная эталонные представления букв, обучить нейронную сеть, а затем использовать ее для распознавания как эталонных, так и тестовых букв.
Для решения задачи обучения нейронной сети использован метод обратного распространения ошибки.
Используется 3-слойная нейронная сеть, структура которой приведена на рис. 2.
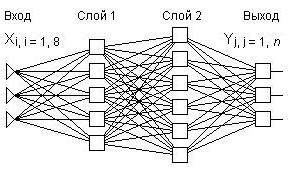
Рис. 2. Структура примененной нейронной сети (n – число распознаваемых букв)
Третий слой образуют выходные нейроны.
В нейронной сети выбранной структуры каждый элемент младшего слоя передает свой выходной сигнал на входы всех элементов следующего слоя.
Число элементов в первом и втором слоях нейронной сети может варьироваться. В частности, в разбираемом примере второй слой содержит 8, а третий – 24 нейрона.
Обе части входных данных (эталонные и тестовые) хранятся в таблице Lttrs.dbf с двумя следующими символьными полями:
Nm (2 символа);
Lttr (63 символа).
В первом поле указывается буква, а во втором – ее представление.
Сначала следуют эталонные буквы, а затем тестовые. Записи в каждой части отсортированы по алфавиту. Буквы в тестовой части таблицы в поле Nm снабжены окончанием в виде цифры 2. Фрагмент таблицы Lttrs (конец эталонной и начало тестовой частей) приведен на рис. 3.
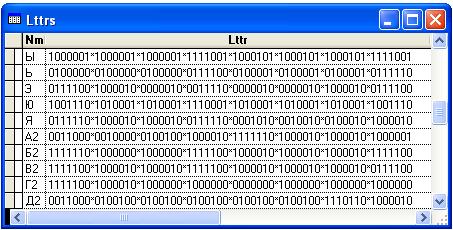
Рис. 3. Таблица входных данных
И эталонная, и тестовые части таблицы имеют по 29 строк (отсутствуют буквы Ё, Й и Щ).
На вход программы распознавания подается номер nT строки тестовой части таблицы. Результатом работы программы является номер nM строки из эталонной части таблицы. Результат положителен, если nT – nM = 29. Так, если на вход подан номер nT = 31 строки, содержащей искаженное представление буквы Б, то правильным решением будет номер nM = 2 строки, содержащей эталонное представление буквы Б.
Программы обучения и распознавания работают с числовыми представлениями букв. Каждая буква – это набор из восьми цифр, отвечающих соответствующим строкам табличного описания буквы (см. рис. 1). В приводимой ниже программе эти цифры записываются в массив rrX0.
Минимальное число в строке табличного представления буквы равно нулю, максимальное – 127. При формировании массива rrX0 (выполняется процедурой GtLttr), число каждой строки табличного представления буквы уменьшается на 63. Таким образом, минимальное значение элемента массива rrX0 равно -63, а максимальное – 64.
Такое смещение обусловлено тем, что при вычислении выходного сигнала нейрона используется логистическая функция, возвращающая значение в диапазоне [-0.5, 0.5]. Смещение согласовывает входы и выходы нейронной сети.
Таким образом, на вход сети подаются 8 сигналов, описывающих распознаваемую букву. Так, в случае искаженной буквы Ж, на входе окажутся показанные на рис. 4 сигналы, уменьшенные на величину смещения.
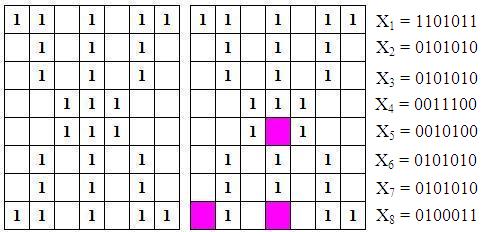
Рис. 4. Буква Ж и ее представление на входе нейронной сети
Число выходов нейронной сети равно числу букв в обучающей выборке. В примере формируется нейронная сеть, способная распознавать первые 10 букв русского алфавита.
Значения выходных сигналов находятся в диапазоне [-0.5, 0.5].
После обработки сигнала выбирается выход с максимальным сигналом. По номеру этого выхода в эталонной части таблицы Lttrs находится решение задачи. Так, в случае буквы Ж абсолютно верным решением будет вектор y, в котором 7-й элемент равен 0.5, а все прочие элементы имеют значение -0.5.
Сигнал, подаваемый на вход элемента нейронной сети слоя k, определяется, как взвешенная сумма его входных сигналов:
skj = ∑mi=1yiwkij, j = 1, nk, где
m – число элементов (нейронов) в слое k – 1. В случае первого слоя m = 8, а yi – это входные сигналы (yi = xi);
nk – число элементов в слое k;
wkij – соответствующий весовой коэффициент.
Выход каждого элемента рассчитывается по следующей формуле:
yjk = f(sjk), где
f(x) = -0.5 + 1 / (1 + e-αx) (в нижеприводимой программе α = 1.0) .
Функция f называется логистической, ее график приведен на рис. 5.
Рис. 5. Использованная в примере логистическая функция
Задача обучения нейронной сети состоит в нахождении весовых коэффициентов wkij, обеспечивающих правильное распознавание образов (в нашем случае букв).
Эта задача решается методом обратного распространения ошибки, следующим образом:
δj = (yj - dj)dyj/dsj (в случае выходных нейронов), где dj – ожидаемое значение на j-м выходе,
или
δjk = [∑iδik+1wijk+1]dyj/dsj (для нейронов первого и второго слоев, k = 1 или k = 2).
Производная логистической функции равна αe-αx / (1 + e-αx)2, в программе α = 1.0.
Δwkij = -ηδkjyik-1 (в случае выходного слоя k = 3). В программе η = 0.75.
wkij = wkij + Δwkij.
Приведенная процедура неоднократно выполняется для всего множества эталонных букв, образующих обучающую выборку. Процесс обучения завершается либо при получении весовых коэффициентов, обеспечивающих распознавание всех букв обучающей выборки, либо после превышения заданного порогового числа итераций.
Начальные значения весовых коэффициентов всех нейронов, формируемые перед первой итерацией, задаются случайным образом в диапазоне [0.0, 1.0].
Обучающая выборка формируется в примере из 10 первых букв таблицы Lttrs.
На вход нейронной сети подается вектор x (размер вектора 8), содержащий числовое представление распознаваемой буквы. На выходе сети, по известным, найденным в процессе обучения весовым коэффициентам вычисляется вектор y (размер вектора 10).
Решение дает выходной нейрон с максимальным значением yj: по номеру j этого нейрона из таблицы Lttrs извлекается и предъявляется в качестве ответа буква.
Весовые коэффициенты хранятся в таблице Wghts.dbf, имеющей следующие поля:
Lr (тип Integer) – номер слоя;
D (тип Integer) – номер нейрона в слое;
D2 (тип Integer) – номер подходящей к нейрону связи;
W (тип Numeric 18, 10) – значение весового коэффициента.
Фрагмент таблицы показан на рис. 6.
Рис. 6. Таблица весовых коэффициентов (фрагмент)
Приводимый ниже код состоит из двух головных программ.
Первая используется для обучения нейронной сети. В результате ее работы формируется таблица весовых коэффициентов. Параметрами программы являются число элементов в первом и втором слоях сети, размер обучающей выборки и параметры алгоритма обучения.
Вторая головная программа запускается для оценки качества сформированной нейронной сети. Последовательно на вход сети подаются тестовые буквы, сеть вычисляет ответ, и он сравнивается с известным точным результатом.
Также код включает общие процедуры, то есть используемые как обучающей, так и тестовой программами, и процедуры целевого назначения, то есть вызываемые либо обучающей, либо тестовой программой.
* Возвращает значение логистической функции
FUNCTION sgmd
LPARAMETERS x, a
a = IIF(PARAMETERS() = 1, 1.0, a)
DO CASE
CASE x > 10.0
f = 0.5
CASE x < -10.0
f = -0.5
OTHERWISE
f = 1.0 / (1.0 + EXP(-a * x)) - 0.5
ENDCASE
RETURN f
ENDFUNC
* Расчет выходных значений нейронов
PROCEDURE fndX(rrXPrv, rrW, rrXNn, nRsltM, jc, prn, rrPrn)
LOCAL k, k2
nn = ALEN(rrW, 1)
nPrv = ALEN(rrW, 2)
FOR k = 1 TO nn
s = 0.0
FOR k2 = 1 TO nPrv
s = s + rrW[k, k2] * rrXPrv[k2]
NEXT
rrXNn[k] = sgmd(s)
NEXT
* Подготовка массива rrXNn для последующей печати
IF prn
mVl = rrXNn[1]
kM = 1
FOR k = 1 TO nn
IF mVl < rrXNn[k]
mVl = rrXNn[k]
kM = k
ENDIF
NEXT
tptVls = ''
FOR k = 1 TO nn
tptVls = tptVls + ' ' + TRANSFORM(ROUND(rrXNn[k], 2), '99.99')
NEXT
lttrTst = lttrs.Nm
GO kM IN lttrs
rrPrn[jc] = IIF(kM = jc, ‘+ ’, ‘- ‘) + lttrTst + ' : ' + lttrs.Nm + ' : ';
+ TRANSFORM(ROUND(rrXNn[kM], 2), '99.99') + ' : ' + tptVls
nRsltM = nRsltM + IIF(kM = jc, 1, 0)
ENDIF
ENDPROC
* Формирует массив rrX с числовым представлением буквы
* Элементы массива – суть вектор, подаваемый на вход нейронной сети
PROCEDURE gtLttr
LPARAMETERS rrX, xM
LOCAL k, j
mLlttr = lttrs.Lttr
FOR k = 1 TO 8
wrd = GETWORDNUM(mLlttr, k, "*")
vl = 0
FOR j = 1 TO 7
p = SUBSTR(wrd, j, 1)
vl = vl + IIF(p = '1', 2^(j - 1), 0)
NEXT
rrX(k) = (-0.5 * xM + vl) / xM
NEXT
ENDPROC
* Выводит в файл d:1.txt результат работы программы
* Параметр rCntLrn – это число распознаваемых букв
* Массив rrFnd имеет rCntLrn элементов, каждый из которых содержит
* плюс, если результат верен, и минус – в противном случае,
* исходную букву, букву – ответ, значение выходного сигнала,
* соответствующего ответу, последовательность всех выходных значений
* После вывода массива печатаются процент распознавания и время работы программы
PROCEDURE prntRsltNN(rCntLrn, rrPrn, nRsltM, tStrt)
SET SAFETY OFF
SET ALTERNATE TO d:1.txt
SET ALTERNATE ON
SET CONSOLE OFF
FOR k = 1 TO rCntLrn
? rrPrn[k]
NEXT
? "Success = " + TRANSFORM(ROUND(100.0 * nRsltM / rCntLrn, 2)) + "%"
? 'Time = ' + TRANSFORM(SECONDS( ) - tStrt)
SET ALTERNATE TO
MODIFY FILE d:1.txt
ENDPROC
* Возвращает значение производной логистической функции
FUNCTION sgmdD
LPARAMETERS x, a
a = IIF(PARAMETERS() = 1, 1.0, a)
f = EXP(-a * x)
f2 = 1.0 + f
f2 = f2 * f2
fD = a * f / f2
RETURN fD
ENDFUNC
* Формирует начальные значения весовых коэффициентов
PROCEDURE ntW(nPrv, nn, rrW, lrVl, prn)
FOR k = 1 TO nn
wVl = ''
FOR k2 = 1 TO nPrv
rrW[k, k2] = RAND()
* Подготовка печати весовых коэффициентов
IF lrVl = 1
wVl = wVl + ' ' + TRANSFORM(ROUND(rrW[k, k2], 4))
ENDIF
NEXT
* Печать весовых коэффициентов
IF lrVl = 1 AND prn
? wVl
ENDIF
NEXT
ENDPROC
* Формирует данные (массивы rrChW и rrNP), необходимые для пересчета
* весовых коэффициентов текущего слоя нейронной сети
PROCEDURE nxtLr(kL, nPrv, n, nn, rrX, rrN, rrW, rrXP, rrNP, rrChW)
LOCAL k, k2
FOR k = 1 TO n
smR = 0
FOR k2 = 1 TO nn
smR = smR + rrN[k2] * rrW[k2, k]
NEXT
rrVl = smR * sgmdD(rrX[k])
FOR k2 = 1 TO nPrv
rrChW[k, k2] = -kL * rrVl * rrXP[k2]
NEXT
rrNP[k] = rrVl
NEXT
ENDPROC
* Выполняет пересчет весовых коэффициентов текущего слоя нейронной сети
PROCEDURE crW(nPrv, nn, rrW, rrChW)
LOCAL k, k2
FOR k = 1 TO nn
FOR k2 = 1 TO nPrv
rrW[k, k2] = rrW[k, k2] + rrChW[k, k2]
NEXT
NEXT
ENDPROC
* Записывает в таблицу Wghts полученные в результате обучения весовые коэффициенты
PROCEDURE wVlSv(nPrv, nn, rrW, lrVl, prn)
DIMENSION rrWNsrt[4]
rrWNsrt[1] = lrVl
SELECT wghts
IF lrVl = 1
DELETE ALL
PACK
ENDIF
FOR k = 1 TO nn
rrWNsrt[2] = k
wVl = ''
FOR k2 = 1 TO nPrv
rrWNsrt[3] = k2
rrWNsrt[4] = rrW[k, k2]
APPEND FROM ARRAY rrWNsrt
IF prn
wVl = wVl + ' ' + TRANSFORM(ROUND(rrW[k, k2], 4))
ENDIF
NEXT
IF prn
? wVl
ENDIF
NEXT
ENDPROC
* Формирует массив из двух элементов, содержащий число элементов
* текущего и последующего слоев нейронной сети
PROCEDURE rrDmnsn(lrVl, rrD, prn)
SELECT wghts
CALCULATE CNT() FOR lr = lrVl TO rrCnt
CALCULATE CNT() FOR lr = lrVl AND d = 1 TO dVl
rrD[1] = rrCnt / dVl
rrD[2] = dVl
IF prn
? TRANSFORM(rrD[1]) + ', ' + TRANSFORM(rrD[2])
ENDIF
ENDPROC
* Заполняет массивы весовых коэффициентов нейронной сети
PROCEDURE wVlRd(rrW, lrVl, prn)
SELECT wghts
SCAN FOR wghts.Lr = lrVl
rrW[wghts.D, wghts.D2] = wghts.W
ENDSCAN
* Печать весовых коэффициентов при prn = .T.
IF prn
nn = ALEN(rrW, 1)
nPrv = ALEN(rrW, 2)
FOR k = 1 TO nn
wVl = ''
FOR k2 = 1 TO nPrv
wVl = wVl + ' ' + TRANSFORM(ROUND(rrW[k, k2], 4))
NEXT
? wVl
NEXT
ENDIF
ENDPROC
tStrt = SECONDS( )
CLEAR
IF USED('lttrs')
USE IN lttrs
ENDIF
IF USED('wghts')
USE IN wghts
ENDIF
USE lttrs IN 1
USE wghts IN 2
SELECT lttrs
* Предельное число обучающих итераций
nLrn = 300
kL = 0.75
* Размер обучающей выборки
rCntLrn = 10
* Число букв в эталонной части таблице Lttrs
lttrsLL = 29
* Число входных сигналов и элементов в слоях нейронной сети
n0 = 8
n1 = 8
n2 = 24
n3 = rCntLrn
* Величина смещения в описании буквы
xM = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 + 2^5 && 63
* Массив с описание распознаваемой буквы
DIMENSION rrX0(n0)
* Массивы весовых коэффициентов и поправочных данных
DIMENSION rrW1(n1, n0), rrX1(n1), rrChW1(n1, n0), rr1(n1)
DIMENSION rrW2(n2, n1), rrX2(n2), rrChW2(n2, n1), rr2(n2)
DIMENSION rrW3(n3, n2), rrX3(n3), rrChW3(n3, n2), rr3(n3)
* Массив выходных сигналов, отвечающих абсолютно верному решению
DIMENSION rrX3Rght(n3)
* Массив с выводимыми на печать данными
DIMENSION rrPrn(rCntLrn)
* Инициализация массивов поправочных данных
rrChW1 = 0
rrChW2 = 0
rrChW3 = 0
* Генерация начальных весовых коэффициентов
ntW(n0, n1, @rrW1, 1, .F.)
ntW(n1, n2, @rrW2, 2)
ntW(n2, n3, @rrW3, 3)
* Обучение
FOR jc0 = 1 TO nLrn
FOR jc = 1 TO rCntLrn
rrX3Rght = -0.5
rrX3Rght[jc] = 0.5
FOR jc2 = 1 TO 2
GO jc
* Формируем числовое представление текущей буквы
* Рассчитываем нейронную сеть
gtLttr(@rrX0, xM)
fndX(@rrX0, @rrW1, @rrX1)
fndX(@rrX1, @rrW2, @rrX2)
fndX(@rrX2, @rrW3, @rrX3)
* Получаем корректирующие значения выходных нейронов
FOR k = 1 TO n3
s3 = rrX3[k]
rrVl = (s3 - rrX3Rght[k]) * sgmdD(s3)
FOR k2 = 1 TO n2
rrChW3[k, k2] = -kL * rrVl * rrX2[k2]
NEXT
rr3[k] = rrVl
NEXT
* Получаем корректирующие значения нейронов прочих уровней сети
nxtLr(kL, n1, n2, n3, @rrX2, @rr3, @rrW3, @rrX1, @rr2, @rrChW2)
nxtLr(kL, n0, n1, n2, @rrX1, @rr2, @rrW2, @rrX0, @rr1, @rrChW1)
* Корректировка весовых коэффициентов
crW(n0, n1, @rrW1, @rrChW1)
crW(n1, n2, @rrW2, @rrChW2)
crW(n2, n3, @rrW3, @rrChW3)
NEXT
NEXT
* Расчет нейронной сети для всех букв обучающей выборки
* с целью оценки качества обучения (nRsltM - число точных решений)
nRsltM = 0
FOR jc = 1 TO rCntLrn
GO jc
gtLttr(@rrX0, xM)
fndX(@rrX0, @rrW1, @rrX1)
fndX(@rrX1, @rrW2, @rrX2)
fndX(@rrX2, @rrW3, @rrX3, @nRsltM, jc, .F., 2)
NEXT
* Завершаем обучение, если сеть узнает все буквы обучающей выборки
IF nRsltM = rCntLrn
EXIT
ENDIF
NEXT
* Проверка качества сети на буквах обучающей выборки
SELECT lttrs
nRsltM = 0
FOR jc = 1 TO rCntLrn
GO jc
gtLttr(@rrX0, xM)
fndX(@rrX0, @rrW1, @rrX1)
fndX(@rrX1, @rrW2, @rrX2)
fndX(@rrX2, @rrW3, @rrX3, @nRsltM, jc, .T., @rrPrn)
NEXT
* Печать результатов проверки
prntRsltNN(rCntLrn, @rrPrn, nRsltM, tStrt)
wVlSv(n0, n1, @rrW1, 1, .F.)
wVlSv(n1, n2, @rrW2, 2, .F.)
wVlSv(n2, n3, @rrW3, 3, .F.)
Заметим, что обучение можно продолжить и при достижении условия nRsltM = rCntLrn, добавив значимое число итераций.
После завершения поиска весовых коэффициентов нейронной сети обучающая выборка вновь подается на вход сети для оценки результатов обучения.
В примере распознаются все элементы обучающей выборки:
+ A : A : 0.42 : 0.42 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50
+ Б : Б : 0.48 : -0.44 0.48 -0.50 -0.48 -0.48 -0.47 -0.50 -0.50 -0.49 -0.49
+ B : B : 0.47 : -0.44 -0.50 0.47 -0.49 -0.46 -0.50 -0.49 0.18 -0.48 -0.49
+ Г : Г : 0.41 : -0.50 -0.47 -0.50 0.41 -0.48 -0.50 -0.50 -0.45 -0.50 -0.46
+ Д : Д : 0.46 : -0.48 -0.50 -0.49 -0.49 0.46 -0.50 -0.50 -0.47 -0.50 -0.50
+ E : E : 0.38 : -0.50 -0.50 -0.50 -0.50 -0.50 0.38 -0.49 -0.50 -0.50 -0.50
+ Ж : Ж : 0.47 : -0.50 -0.50 -0.50 -0.50 -0.50 -0.48 0.47 -0.50 -0.50 -0.49
+ З : З : 0.04 : -0.50 -0.50 -0.49 -0.50 -0.50 -0.50 -0.50 0.04 -0.50 -0.50
+ И : И : 0.48 : -0.41 -0.49 -0.43 -0.50 -0.50 -0.48 -0.50 -0.40 0.48 -0.43
+ K : K : 0.44 : -0.50 -0.50 -0.50 -0.48 -0.50 -0.47 -0.50 -0.38 -0.50 0.44
Success = 100%
Time = 31.11
Время, затраченное на обучение, выводится в секундах.
tStrt = SECONDS( )
CLEAR
SET TALK OFF
* Если параметр frmTst = .T., то оценка сети будет выполнена по тестовой выборке,
* то есть буквы будут взяты из тестовой части таблицы Lttrs
frmTst = .T.
IF USED('lttrs')
USE IN lttrs
ENDIF
IF USED('wghts')
USE IN wghts
ENDIF
USE lttrs IN 1
USE wghts IN 2
* Величина смещения в описании буквы
xM = 2^0 + 2^1 + 2^2 + 2^3 + 2^4 + 2^5 && 63
* Получаем размеры нейронной сети (число входов и число элементов в каждом ее слое)
SELECT lttrs
DIMENSION rrD(2)
rrDmnsn(1, @rrD, .F.)
n0 = rrD[2]
n1 = INT(rrD[1])
rrDmnsn(2, @rrD, .F.)
n2 = INT(rrD[1])
rrDmnsn(3, @rrD, .F.)
n3 = INT(rrD[1])
DIMENSION rrX0(n0)
DIMENSION rrW1(n1, n0), rrX1(n1)
DIMENSION rrW2(n2, n1), rrX2(n2)
DIMENSION rrW3(n3, n2), rrX3(n3)
DIMENSION rrPrn(n3)
* Записываем весовые коэффициенты нейронной сети в массивы
wVlRd(@rrW1, 1, .F.)
wVlRd(@rrW2, 2, .F.)
wVlRd(@rrW3, 3, .F.)
* Проверка
SELECT lttrs
nRsltM = 0
FOR jc = 1 TO n3
GO jc + IIF(frmTst, 29, 0)
gtLttr(@rrX0, xM)
fndX(@rrX0, @rrW1, @rrX1)
fndX(@rrX1, @rrW2, @rrX2)
fndX(@rrX2, @rrW3, @rrX3, @nRsltM, jc, .T., @rrPrn)
NEXT
* Печать результатов проверки
prntRsltNN(n3, @rrPrn, nRsltM, tStrt)
При работе с тестовыми (искаженными) буквами процент распознавания снижается:
+ A2 : A : 0.50 : 0.50 0.50 0.48 -0.50 0.49 0.50 0.17 -0.49 0.50 0.44
– Б2 : З : -0.50 : -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50
+ B2 : B : 0.29 : -0.49 -0.50 0.29 -0.50 -0.49 -0.50 -0.50 0.06 -0.50 -0.50
+ Г2 : Г : 0.42 : -0.50 -0.47 -0.50 0.42 -0.48 -0.50 -0.50 -0.45 -0.50 -0.46
+ Д2 : Д : 0.47 : -0.40 -0.46 -0.50 -0.36 0.47 -0.50 -0.50 -0.44 -0.50 -0.35
+ E2 : E : 0.34 : -0.50 -0.50 -0.50 -0.50 -0.50 0.34 -0.49 -0.50 -0.50 -0.49
+ Ж2 : Ж : 0.45 : -0.50 -0.50 -0.50 -0.49 -0.50 -0.41 0.45 -0.50 -0.50 -0.49
+ З2 : З : -0.45 : -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.45 -0.50 -0.50
– И2 : З : -0.49 : -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.49 -0.50 -0.50
+ K2 : K : -0.46 : -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.50 -0.46
Success = 80%
Time = 0.015
В примере таблица Lttrs содержит следующие 58 строк:
A 0011000*0011000*0100100*1000010*1111110*1000010*1000010*1000010
Б 1111100*1000000*1000000*1111100*1000010*1000010*1000010*1111100
B 1111100*1000010*1000010*1111100*1000010*1000010*1000010*1111100
Г 1111100*1000010*1000000*1000000*1000000*1000000*1000000*1000000
Д 0011000*0100100*0100100*0100100*0100100*0100100*1111110*1000010
E 1111110*1000000*1000000*1111100*1000000*1000000*1000000*1111110
Ж 1101011*0101010*0101010*0011100*0011100*0101010*0101010*1101011
З 0111100*1000010*0000010*0011100*0000010*0000010*1000010*0111100
И 1000010*1000010*1000110*1001010*1010010*1100010*1000010*1000010
K 1000010*1000100*1001000*1010000*1110000*1001000*1000100*1000010
Л 0000110*0001010*0010010*0010010*0010010*0010010*0100010*1000010
M 1000001*1100011*1010101*1001001*1000001*1000001*1000001*1000001
H 1000010*1000010*1000010*1111110*1000010*1000010*1000010*1000010
O 0111100*1000010*1000010*1000010*1000010*1000010*1000010*0111100
П 1111110*1000010*1000010*1000010*1000010*1000010*1000010*1000010
P 1111100*1000010*1000010*1111100*1000000*1000000*1000000*1000000
C 0111100*1000010*1000000*1000000*1000000*1000000*1000010*0111100
T 1111100*0010000*0010000*0010000*0010000*0010000*0010000*0010000
У 1000010*1000010*1000010*0111110*0000010*0000010*1000010*0111100
Ф 0001000*0111110*1001001*1001001*0111110*0001000*0001000*0001000
X 1000001*0100010*0010100*0001000*0001000*0010100*0100010*1000001
Ч 1000010*1000010*1000010*0111110*0000010*0000010*0000010*0000010
Ш 1001001*1001001*1001001*1001001*1001001*1001001*1001001*1111111
Ъ 1100000*0100000*0100000*0111100*0100001*0100001*0100001*0111110
Ы 1000001*1000001*1000001*1111001*1000101*1000101*1000101*1111001
Ь 0100000*0100000*0100000*0111100*0100001*0100001*0100001*0111110
Э 0111100*1000010*0000010*0011110*0000010*0000010*1000010*0111100
Ю 1001110*1010001*1010001*1110001*1010001*1010001*1010001*1001110
Я 0111110*1000010*1000010*0111110*0001010*0010010*0100010*1000010
A2 0011000*0010000*0100100*1000010*1111110*1000010*1000010*1000001
Б2 1111110*1000000*1000000*1111100*1000010*1000010*1000010*1111100
B2 1111100*1000010*1000010*1111100*1000010*1000010*1000010*0111100
Г2 1111100*1000010*1000000*1000000*0000000*1000000*1000000*1000000
Д2 0011000*0100100*0100100*0100100*0100100*0100100*1110110*1000010
E2 1111110*1000000*1000000*1101100*1000000*1000000*1000000*1111110
Ж2 1101011*0101010*0101010*0011100*0010100*0101010*0101010*0100011
З2 0111100*1000010*0000010*0011100*0000010*0000010*1000010*0110100
И2 1000010*1000010*1000110*1000010*1010010*1100010*1000010*1000010
K2 1000001*1000100*1001000*1010000*1110000*1001000*1000100*1000010
Л2 0000110*0001010*0010010*0010010*0010010*0010010*0100010*1000000
M2 1000001*1100011*1010101*1001001*1000001*1000001*1000001*1000000
H2 1000010*1000010*1000010*1101110*1000010*1000010*1000010*1000010
O2 0110100*1000010*1000010*1000010*1000010*1000010*1000010*0111100
П2 1111110*1000010*1000010*1000010*1000010*1000010*1000010*1000000
P2 1101100*1000010*1000010*1111100*1000000*1000000*1000000*1000000
C2 0110100*1000010*1000000*1000000*1000000*1000000*1000010*0111100
T2 1111111*0010000*0010000*0010000*0010000*0010000*0010000*0010000
У2 1000010*1000010*1000010*0111010*0000010*0000010*1000010*0111100
Ф2 0001000*0111110*1001001*1001001*0110110*0001000*0001000*0001000
X2 1000001*0100010*0010100*0001000*0001000*0010100*0100010*1001001
Ч2 1000010*1000010*1000010*0111110*0000010*0000010*0000010*0000000
Ш2 1001001*1001001*1001001*1001001*1001001*1001001*1001001*1110111
Ъ2 1100000*0000000*0100000*0111100*0100001*0100001*0100001*0111110
Ы2 1000001*1000001*1000001*1111001*1000101*1000101*1000100*1111001
Ь2 0100000*0100000*0100000*0111100*0100001*0100001*0100001*0110110
Э2 0111110*1000010*0000010*0011110*0000010*0000010*1000010*0111100
Ю2 1001110*1010001*1010001*1110001*1010001*1010001*1010001*1001011
Я2 0111110*1000010*1000010*0111110*0001010*0010010*0100010*1000000
Приведенная программа содержит около 300 строк, что несколько больше, чем в случае генетического алгоритма.
Совсем необязательно обучать сеть распознавать все буквы. Проще (с позиции обучения) иметь, например, три сети, каждая из которых обучена распознаванию своего подмножества букв алфавита. Образ поочередно подается на вход каждой сети. В качестве решения берется буква, отвечающая нейрону с максимальным значением выходного сигнала.