Создается C#-приложение, в котором средствами IMSL решается задача оптимизации портфеля инвестиций. Объектом инвестиций могут быть, например, ценные бумаги (далее активы).
Ожидаемая доходность актива:
E(Ri) = ∑(i)Ri / n,
где
Ri – доходность актива в i-м периоде;
n – число периодов наблюдения (периоды имеют одинаковую продолжительность).
Если в портфеле несколько активов, то его ожидаемая доходность равна
E(Rp) = ∑(i)wiE(Ri),
где
E(Ri) – ожидаемая доходность i-го актива;
wi – доля i-го актива в портфеле.
Риск получить доходность, отличную от ожидаемой, вычисляется как дисперсии случайной величины
σ2 = ∑(i)(Ri – R)2 / n,
где
R – средняя доходность актива (математическое ожидание);
Ri – доходность актива в i-м периоде;
n – число периодов наблюдения.
Квадратный корень из дисперсии (σ) называется среднеквадратичным отклонением.
Риск портфеля нельзя определять как среднее значение дисперсий всех активов портфеля ввиду взаимосвязанности последних, которая фиксируется таким показателем, как ковариация.
Ковариация активов X и Y:
covxy = ∑(i)(Rxi – Rx) (Ryi – Ry) / n
Если доходности активов изменяются в одном направлении, то их ковариация положительна, если – в разных, то отрицательна. Если активы не связаны, то их ковариация равна нулю.
Ковариация случайной величины с собой равна ее дисперсии.
Риск портфеля, состоящего из двух активов:
σp2 = wx2σx2 + wy2σy2 + 2wxwycovxy
Общая формула расчета риска портфеля:
σp2 = ∑(i)∑(j)wiwjcovij = ∑(i)wi2σi2 + ∑(i)∑(j≠i) wiwjcovij
Риск портфеля уменьшается, если его активы слабокореллированны.
Включение в портфель активов с низкой корреляцией называется его диверсификацией.
Риск, ниже которого нельзя опуститься, называется недиверсифицируемым.
Заметим, что для расчета ожидаемой доходности и риска требуются надежные статистические данные, собранные на достаточно большом отрезке наблюдения.
Желание инвестора – иметь портфель с наибольшей доходностью и наименьшим риском при условии соблюдения всех ограничений.
В приводимой ниже программе эта задача решается следующим образом (задача решается для портфеля с четырьмя активами).
На входе имеем:
Решение ведется по следующей схеме:
Результат для заданного в программе ожидаемого возврата портфеля показан на рис. 1.
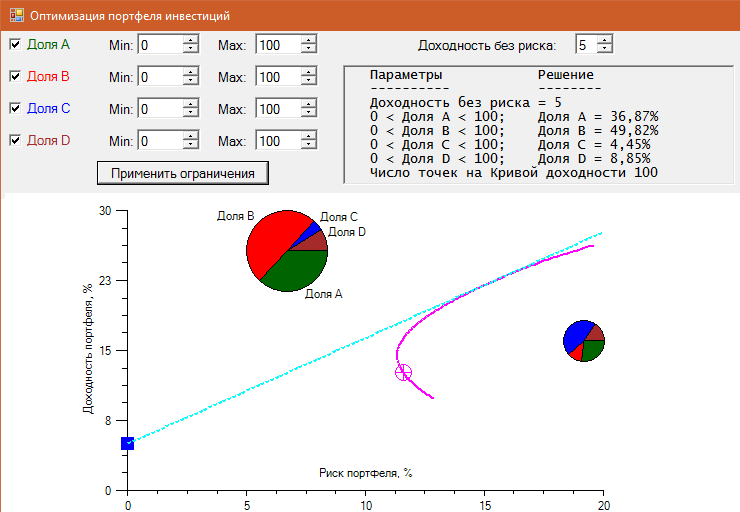
Рис. 1. Оптимизация портфеля инвестиций
Маленькая круговая диаграмма, показанная в правой части рис. 1, отвечает точке положения мыши на Кривой доходности.
Если мышь увести в сторону от Кривой доходности, то малая круговая диаграмма исчезнет.
Тип проекта - Windows Form Application. Форма, создаваемая при начале нового проекта, и весь связанный с ней код удаляются. Взамен используется приводимая в следующем разделе программа.
Форма, наблюдаемая на рис. 1, генерируется этой программой. Детали построения формы см. в приводимом коде и сопутствующем комментарии.
Подключение недостающих ссылок осуществляется обычным способом: Solution Explorer – References – правая кнопка мыши – Add Reference.
Приводимый код основан на примере, имеющемся в проекте IMSLDemo, поставляемом с библиотекой C#-IMSL.
using System;
using System.Drawing; // Color
using System.Windows.Forms;
using Imsl.Chart2D;
using Imsl.Stat; // Covariances
using Imsl.Math;
namespace WindowsFormsApplicationIMSL
{
static class Program
{
// Точка входа приложения
[STAThread]
static void Main()
{
Application.Run(new PortfolioOptimization());
}
}
public class PortfolioOptimization : System.Windows.Forms.Form, ChartFunction
{
private double[,] solution;
private int optimalIndex, oldIndex;
private double slope, intercept;
private String[] names = { "Доля A", "Доля B", "Доля C", "Доля D" };
private double[] riskRange;
private int[] oldmin = new int[4];
private int[] oldmax = new int[4];
private bool isNaN;
private CheckBox[] cb = new CheckBox[4];
private NumericUpDown[] nud = new NumericUpDown[8];
private Color[] clr = { Color.DarkGreen, Color.Red, Color.Blue, Color.Brown };
private System.Windows.Forms.Label label9;
private System.Windows.Forms.NumericUpDown numericUpDown9;
private System.Windows.Forms.Button button1;
private System.Windows.Forms.RichTextBox richTextBox1;
private Imsl.Chart2D.PanelChart panelChart1;
private Imsl.Chart2D.Chart chart;
private Imsl.Chart2D.AxisXY axis;
private Pie pie, miniPie;
private Data mousePoint;
public PortfolioOptimization()
{
InitializeComponent();
this.AcceptButton = button1;
SetupChart();
DoAll();
}
// Находит кривую доходности, оптимальный портфель
// Очищает и выводит график и прочие данные и обновляет текст с решением
private void DoAll()
{
if (!CheckSliders()) return;
RunEfficient();
ClearChart();
if (solution[0, 0].Equals(Double.NaN))
{
PopWarning("Задача не имеет решения, удовлетворяющего всем ограничениям");
isNaN = true;
if (pie != null) pie.Remove();
Refresh();
}
else
{
isNaN = false;
optimalIndex = FindOptimalIndex();
int len = solution.GetLength(1);
double[] risk = new double[len];
double[] ret = new double[len];
riskRange = new double[2] { solution[0, 0], solution[0, 0] };
for (int i = 0; i < len; i++)
{
risk[i] = solution[0, i];
ret[i] = solution[1, i];
if (risk[i] < riskRange[0]) riskRange[0] = risk[i];
if (risk[i] > riskRange[1]) riskRange[1] = risk[i];
}
PlotEfficientFrontier(risk, ret);
}
richTextBox1.Text = BuildPlainText();
}
// Задает параметры диаграммы и обработчики событий мыши MouseMove и MouseLeave
private void SetupChart()
{
chart = panelChart1.Chart;
axis = new AxisXY(chart);
string pc = System.Globalization.CultureInfo.CurrentCulture.NumberFormat.PercentSymbol;
axis.AxisX.AxisTitle.SetTitle("Риск портфеля, " + pc);
axis.AxisY.AxisTitle.SetTitle("Доходность портфеля, " + pc);
axis.AxisX.TextFormat = "#0";
axis.AxisY.TextFormat = "#0";
axis.AxisX.AutoscaleInput = AxisXY.AUTOSCALE_OFF;
axis.AxisY.AutoscaleInput = AxisXY.AUTOSCALE_OFF;
axis.AxisX.SetWindow(0.0, 20.0);
axis.AxisY.SetWindow(0.0, 30.0);
// Обработчики событий мыши
panelChart1.MouseMove += new MouseEventHandler(panelChart1_MouseMove);
panelChart1.MouseLeave += new EventHandler(panelChart1_MouseLeave);
}
// Находит кривую доходности
private void RunEfficient()
{
int numVars = 4;
EfficientFrontier ef = new EfficientFrontier(numVars);
// Матрица коэффициентов корреляции активов
double[,] cov = new double[,] {{0.0022264210, 0.0000093276, 0.0000099678, 0.0000299572},
{0.0000093276, 0.0033981300, 0.0000107892, 0.0000169680},
{0.0000099678, 0.0000107892, 0.0017038160, 0.0000143299},
{0.0000299572, 0.0000169680, 0.0000143299, 0.0044181270}};
// Ожидаемый результат
double[] expectedReturn = new double[] { 0.0009369806, 0.0016386612, 0.0003375174, 0.0005914344 };
for (int i = 0; i < expectedReturn.Length; i++)
{
expectedReturn[i] /= 2.0;
cov[i, i] *= 20.0;
}
ef.SetCovarianceMatrix(cov);
ef.SetExpectedReturns(expectedReturn);
double[,] b = new double[numVars, 2];
int m = -2;
for (int k = 0; k < 4; k++)
{
m += 2;
b[k, 0] = (double)nud[m].Value / 100.0;
b[k, 1] = (double)nud[m + 1].Value / 100.0;
}
ef.SetBounds(b);
ef.Compute();
solution = ef.GetSolution();
// Преобразуем доходность за день в годовую доходность
for (int i = 0; i < solution.GetLength(1); i++)
{
solution[0, i] *= 100.0; // Проценты
solution[1, i] *= (365.0 * 100.0); // Годовая доходность
}
}
// Находит оптимальное решение по кривой доходности и точки Доходность без риска -
// это точка из массива solution на Кривой доходности, ближайшая к точке,
// через которую проходит касательная к этой кривой
private int FindOptimalIndex()
{
double difference;
double leastDifference = 1e6;
int bestLocation = solution.GetLength(1) - 1;
for (int i = solution.GetLength(1) - 2; i > 1; i--)
{
slope = (solution[1, i + 1] - solution[1, i - 1]) / (solution[0, i + 1] - solution[0, i - 1]);
if (slope < 0.0) i = 0;
intercept = solution[1, i] - slope * solution[0, i];
difference = System.Math.Abs(intercept - (int)numericUpDown9.Value);
if (difference < leastDifference)
{
leastDifference = difference;
bestLocation = i;
}
}
return bestLocation;
}
// Рисует кривую доходности портфеля, касательную к ней из точки доходности без риска,
// круговую диаграмму, отвечающую оптимальному решению
private void PlotEfficientFrontier(double[] risk, double[] ret)
{
int riskFreeRate = (int)numericUpDown9.Value;
// Кривая доходности портфеля
Data efData = new Data(axis, risk, ret);
efData.DataType = Data.DATA_TYPE_LINE;
efData.LineColor = Color.Magenta;
efData.LineWidth = 2.0;
// Выводим маркер в точке Доходность без риска (находится на оси Y)
Data rfData = new Data(axis, new double[] { 0.0 }, new double[] { riskFreeRate });
rfData.DataType = Data.DATA_TYPE_MARKER;
rfData.MarkerType = Data.MARKER_TYPE_FILLED_SQUARE;
rfData.MarkerColor = Color.Blue;
// Касательная к кривой доходности из точки Доходность без риска
double x = solution[0, optimalIndex];
double y = solution[1, optimalIndex];
intercept = riskFreeRate; // Точка пересечения касательной с осью Y
slope = (y - riskFreeRate) / x; // Наклон касательной
Data tanData = new Data(axis, this, 0, 20); // 0, 20 - диапазон по оси X
tanData.LineColor = Color.Cyan;
tanData.LineWidth = 2.0;
tanData.SetLineDashPattern(new double[] { 2, 10 }); // Пунктирная линия
AddPieChart();
Refresh();
}
// Круговая диаграмма для оптимальной точки
private void AddPieChart()
{
double[] y = {100 * solution[2, optimalIndex], 100 * solution[3, optimalIndex], 100 * solution[4, optimalIndex], 100 * solution[5, optimalIndex]};
if (pie != null) pie.Remove();
pie = new Pie(chart, y);
pie.LabelType = Pie.LABEL_TYPE_TITLE;
pie.SetViewport(0.25, 0.55, 0.05, 0.35);
PieSlice[] slice = pie.GetPieSlice();
for (int k = 0; k < 4; k++)
{
slice[k].SetTitle(names[k]);
slice[k].FillColor = clr[k];
}
}
// Добавляет круговую диаграмму, отвечающую выбранной точке на кривой доходности
// (выбранной точке массива solution)
private void AddMiniPieChart(int pIndex)
{
double[] y = {100 * solution[2, pIndex], 100 * solution[3, pIndex], 100 * solution[4, pIndex], 100 * solution[5, pIndex]};
if (miniPie != null) miniPie.Remove();
// Круговая диаграмма
miniPie = new Pie(chart, y);
miniPie.SetViewport(0.7, 0.85, 0.35, 0.5);
PieSlice[] slice = miniPie.GetPieSlice();
for (int k = 0; k < 4; k++) slice[k].FillColor = clr[k];
}
// Согласует и проверяет значения параметров
private bool CheckSliders()
{
int totalMin = 0, totalMax = 0, m;
for (int k = 0; k < 4; k++)
{
m = 2 * k;
if (nud[m + 1].Value < nud[m].Value) nud[m + 1].Value = nud[m].Value;
totalMin += (int)nud[m].Value;
totalMax += (int)nud[m + 1].Value;
}
string pc = System.Globalization.CultureInfo.CurrentCulture.NumberFormat.PercentSymbol;
if (totalMin > 100)
{
PopWarning("Решение невозможно: сумма минимальных границ ограничений более 100" + pc);
return false;
}
else if (totalMin == 100)
{
PopWarning("Тривиальное решение: сумма минимальных границ ограничений равна 100" + pc);
return false;
}
else if (totalMax < 100)
{
PopWarning("Решение невозможно: сумма максимальных границ ограничений менее 100" + pc);
return false;
}
else return true;
}
// Соообщение об ошибке
private void PopWarning(String msg)
{
MessageBox.Show(msg, "Warning", MessageBoxButtons.OK, MessageBoxIcon.Warning);
}
// Очищает диаграмму
private void ClearChart()
{
if (axis == null) return;
ChartNode[] children = axis.GetChildren();
for (int i = 0; i < children.Length; i++)
{
if (children[i] is Data) children[i].Remove();
}
}
// Формирует сообщение о значениях параметров
private String BuildPlainText()
{
String format = "P";
System.Text.StringBuilder sb = new System.Text.StringBuilder();
sb.Append(" Параметры\t\tРешение\r\n");
sb.Append(" ----------\t\t--------\r\n");
sb.Append(" Доходность без риска = " + (int)numericUpDown9.Value + "\r\n");
double val;
for (int k = 0; k < 4; k++)
{
sb.Append(" " + nud[2 * k].Value + " < " + names[k] + " < " + nud[2 * k + 1].Value + ";\t");
val = solution[k + 2, optimalIndex];
sb.Append(names[k] + " = " + val.ToString(format) + "\r\n");
}
sb.Append(" Число точек на Кривой доходности " + solution.GetLength(1));
return sb.ToString();
}
private void InitializeComponent()
{
this.label9 = new System.Windows.Forms.Label();
this.numericUpDown9 = new System.Windows.Forms.NumericUpDown();
this.button1 = new System.Windows.Forms.Button();
this.richTextBox1 = new System.Windows.Forms.RichTextBox();
this.panelChart1 = new Imsl.Chart2D.PanelChart();
this.SuspendLayout();
// checkBoxes 1-4
CheckBox cbK;
for (int k = 0; k < 4; k++) cb[k] = new System.Windows.Forms.CheckBox();
int y = 8;
string[] ndx = { "A", "B", "C", "D" };
for (int k = 0; k < 4; k++)
{
cbK = cb[k];
cbK.Checked = true;
cbK.CheckState = System.Windows.Forms.CheckState.Checked;
cbK.Font = new System.Drawing.Font("Microsoft Sans Serif", 9.75F, System.Drawing.FontStyle.Regular, System.Drawing.GraphicsUnit.Point, ((System.Byte)(0)));
cbK.ForeColor = clr[k];
cbK.Location = new System.Drawing.Point(8, y);
y += 32;
cbK.Name = "checkBox" + k;
cbK.Size = new System.Drawing.Size(88, 24);
cbK.TabIndex = 1;
cbK.Text = "Доля " + ndx[k];
cbK.CheckedChanged += new System.EventHandler(this.checkBox_CheckedChanged);
this.Controls.Add(cbK);
}
// Labels 1-8 and numericUpDowns 1-8
Label[] lb = new Label[8];
for (int k = 0; k < 8; k++)
{
lb[k] = new System.Windows.Forms.Label();
nud[k] = new System.Windows.Forms.NumericUpDown();
}
Label lbK;
NumericUpDown nudK;
int x = 136, x2 = 254, v = 0, v2 = 100, xL = 96, xL2 = 208;
y = 8;
for (int k = 0; k < 8; k++)
{
bool k2 = k % 2 == 0;
lbK = lb[k];
lbK.Location = new System.Drawing.Point((k2) ? xL : xL2, y);
lbK.Name = "label" + k;
lbK.Size = new System.Drawing.Size(40, 24);
lbK.TabIndex = 2;
lbK.Text = (k2) ? "Min:" : "Max:";
lbK.TextAlign = System.Drawing.ContentAlignment.MiddleRight;
this.Controls.Add(lbK);
nudK = nud[k];
nudK.Increment = new System.Decimal(new int[] { 5, 0, 0, 0 });
nudK.Location = new System.Drawing.Point((k2) ? x : x2, y);
if (!k2) y += 32;
nudK.Name = "numericUpDown" + k;
nudK.Size = new System.Drawing.Size(64, 22);
nudK.TabIndex = 3;
nudK.Value = new System.Decimal(new int[] { (k2) ? v : v2, 0, 0, 0 });
this.Controls.Add(nudK);
}
//
// numericUpDown9 - задание доходности без риска
this.numericUpDown9.Location = new System.Drawing.Point(584, 8);
this.numericUpDown9.Maximum = new System.Decimal(new int[] { 10, 0, 0, 0 });
this.numericUpDown9.Minimum = new System.Decimal(new int[] { 1, 0, 0, 0 });
this.numericUpDown9.Name = "numericUpDown9";
this.numericUpDown9.Size = new System.Drawing.Size(40, 22);
this.numericUpDown9.TabIndex = 5;
this.numericUpDown9.Value = new System.Decimal(new int[] { 5, 0, 0, 0 });
//
// label9
this.label9.Location = new System.Drawing.Point(408, 8);
this.label9.Name = "label9";
this.label9.Size = new System.Drawing.Size(160, 24);
this.label9.TabIndex = 4;
this.label9.Text = "Доходность без риска:";
this.label9.TextAlign = System.Drawing.ContentAlignment.MiddleRight;
//
// button1
this.button1.Location = new System.Drawing.Point(96, 136);
this.button1.Name = "button1";
this.button1.Size = new System.Drawing.Size(172, 24);
this.button1.TabIndex = 6;
this.button1.Text = "Применить ограничения";
this.button1.Click += new System.EventHandler(this.button1_Click);
//
// Область текста для результата
this.richTextBox1.Font = new System.Drawing.Font("Lucida Console", 10.25F, System.Drawing.FontStyle.Regular, System.Drawing.GraphicsUnit.Point, ((System.Byte)(0)));
this.richTextBox1.Location = new System.Drawing.Point(352, 40);
this.richTextBox1.Name = "richTextBox1";
this.richTextBox1.ReadOnly = true;
this.richTextBox1.ScrollBars = System.Windows.Forms.RichTextBoxScrollBars.None;
this.richTextBox1.Size = new System.Drawing.Size(392, 120);
this.richTextBox1.TabIndex = 7;
this.richTextBox1.Text = "richTextBox1";
//
// Область диаграммы
this.panelChart1.Location = new System.Drawing.Point(0, 168);
this.panelChart1.Name = "panelChart1";
this.panelChart1.Size = new System.Drawing.Size(792, 400);
this.panelChart1.TabIndex = 8;
//
// Элемент PortfolioOptimization
this.AutoScaleBaseSize = new System.Drawing.Size(6, 15);
this.ClientSize = new System.Drawing.Size(792, 566);
this.Controls.Add(this.panelChart1);
this.Controls.Add(this.richTextBox1);
this.Controls.Add(this.button1);
this.Controls.Add(this.numericUpDown9);
this.Controls.Add(this.label9);
this.Font = new System.Drawing.Font("Microsoft Sans Serif", 9.75F, System.Drawing.FontStyle.Regular, System.Drawing.GraphicsUnit.Point, ((System.Byte)(0)));
this.Location = new System.Drawing.Point(64, 64);
this.Name = "PortfolioOptimization";
this.StartPosition = System.Windows.Forms.FormStartPosition.Manual;
this.Text = "Оптимизация портфеля инвестиций";
this.ResumeLayout(false);
}
private void checkBox_CheckedChanged(object sender, System.EventArgs e)
{
String nm = ((CheckBox)sender).Name;
int k = Convert.ToInt32(nm.Substring(8));
NumericUpDown nudK = nud[2 * k], nudK2 = nud[2 * k + 1];
if (!cb[k].Checked)
{
nudK.Enabled = false;
nudK2.Enabled = false;
oldmin[k] = (int)nudK.Value;
oldmax[k] = (int)nudK2.Value;
nudK.Value = 0;
nudK2.Value = 0;
}
else
{
nudK.Enabled = true;
nudK2.Enabled = true;
nudK.Value = oldmin[k];
nudK2.Value = oldmax[k];
}
}
private void button1_Click(object sender, System.EventArgs e)
{
DoAll();
}
private void panelChart1_MouseMove(object sender, MouseEventArgs e)
{
if (isNaN) return;
int p = solution.GetLength(1);
double[] eps = { 1, 1 };
double[] user = new double[2];
axis.MapDeviceToUser(e.X, e.Y, user);
// Найденные нижняя и верхняя границы риска
double[] xRange = { riskRange[0], riskRange[1] };
// Найденные нижняя и верхняя границы доходности (с учетом допуска eps)
double[] yRange = { solution[1, 0] - eps[1], solution[1, p - 1] + eps[1] };
// Возврат, если за мышь пределами найденных границ риска и доходности
if ((user[0] < xRange[0]) || (user[0] > xRange[1]) || (user[1] < yRange[0]) || (user[1] > yRange[1])) return;
// Найдем ближайшую по Y к позиции мыши точку на Кривой доходности
double newDist;
double dist = 10;
int index = -1;
for (int i = 0; i < p; i++)
{
newDist = System.Math.Abs(solution[1, i] - user[1]);
if (newDist < dist)
{
dist = newDist;
index = i;
}
}
// Проверяем X-координату
if (System.Math.Abs(solution[0, index] - user[0]) < eps[0])
{
// Перерисовываем, если мышь переместилась к другой точке решения
if (index != oldIndex)
{
if (mousePoint != null) mousePoint.Remove();
if (miniPie != null) miniPie.Remove();
mousePoint = new Data(axis, new double[] { solution[0, index] }, new double[] { solution[1, index] });
mousePoint.DataType = Data.DATA_TYPE_MARKER;
mousePoint.MarkerType = Data.MARKER_TYPE_CIRCLE_PLUS;
mousePoint.MarkerColor = Color.Magenta;
mousePoint.MarkerSize = 1.5;
AddMiniPieChart(index);
Refresh();
}
}
else
{
if (mousePoint != null) mousePoint.Remove();
if (miniPie != null) miniPie.Remove();
Refresh();
}
oldIndex = index;
}
private void panelChart1_MouseLeave(object sender, EventArgs e)
{
if (isNaN) return;
// Стираем маркер и маленькую круговую диаграмму, если мышь покинула Кривую доходности
if (mousePoint != null) mousePoint.Remove();
if (miniPie != null) miniPie.Remove();
Refresh();
}
public double F(double x)
{
return slope * x + intercept;
}
}
//
public class EfficientFrontier
{
private double[,] varcov, cw, bw, solution;
private double[] expectedReturns;
private int m; // Размер портфеля (число активов в портфеле)
private const int numPortfolios = 100; // Число расчетных точек
// Создает экземпляр Кривой доходности и устанавливает заданные по умолчанию ограничения
// m_ - размер портфеля (число видов ценных бумаг в портфеле)
public EfficientFrontier(int m_)
{
this.m = m_;
// Ограничения по умолчанию на веса в задаче линейного программирования
// Пример для трех переменных:
// 1 0 0
// 0 1 0
// 0 0 1
// 1 1 1
cw = new double[m + 1, m];
for (int i = 0; i < m; i++)
{
cw[i, i] = 1;
cw[m, i] = 1;
}
// Граничные значения весов; задаются в SetBounds
// Пример
// 0 1
// 0 1
// 0 1
// 1 1
// означает, что каждый вес находится в диапазоне [0, 1], а сумма весов равна 1
bw = new double[m + 1, 2];
}
// Вычисляет Кривую доходности и находит решение задачи квадратичного программирования
public void Compute()
{
// Входные данные задачи линейного программирования
int[] cType = new int[m + 1];
double[] b = new double[m + 1];
double[] upperLimit = new double[m + 1];
double[] negativeExpectedReturns = new double[m];
for (int i = 0; i < m + 1; i++)
{
cType[i] = 3; // Вид ограничений; вес между нижней и верхней границами, суммма весов равна 1
b[i] = bw[i, 0];
upperLimit[i] = bw[i, 1];
if (i < m) negativeExpectedReturns[i] = -1 * expectedReturns[i];
}
double[] frontier = new double[numPortfolios];
try
{
DenseLP lp = new DenseLP(cw, b, expectedReturns);
lp.SetUpperLimit(upperLimit);
lp.SetConstraintType(cType);
lp.Solve();
double y = lp.ObjectiveValue; // Значение целевой функции - минимально возможный риск
double[] sl = lp.GetSolution();
lp = new DenseLP(cw, b, negativeExpectedReturns);
lp.SetUpperLimit(upperLimit);
lp.SetConstraintType(cType);
lp.Solve();
double z = lp.ObjectiveValue;
double y0 = y + 1e-4;
double z0 = -1 * z - 1e-4;
sl = lp.GetSolution();
double step = (z0 - y0) / (numPortfolios - 1.0);
for (int i = 0; i < numPortfolios; i++) frontier[i] = i * step + y0;
}
catch
{
throw;
}
// Входные данные задачи квадратичного программирования
// Левая часть (LHS) ограничений равенства
double[,] qaeq = new double[2, m];
for (int i = 0; i < m; i++)
{
qaeq[0, i] = cw[m, i];
qaeq[1, i] = expectedReturns[i];
}
double[,] qa = new double[2 * m, m];
for (int i = 0; i < m; i++)
{
for (int j = 0; j < m; j++)
{
qa[j, i] = cw[j, i];
qa[j + m, i] = -1 * cw[j, i];
}
}
// Левая часть (LHS) ограничений неравенства
// Первый элемент изменяется в процессе решения задачи квадратичного программирования
double[] qbeq = new double[2];
qbeq[0] = bw[m, 1];
qbeq[1] = frontier[0];
// Правая часть (RHS) ограничений неравенства
double[] qb = new double[2 * m];
for (int i = 0; i < m; i++)
{
qb[i] = bw[i, 0];
qb[i + m] = -1 * bw[i, 1];
}
// Употребляет QuadraticProgramming для каждой точки; numPortfolios - число точек
QuadraticProgramming qp = null;
double[] qg = new double[m];
solution = new double[numPortfolios, m + 2];
for (int i = 0; i < numPortfolios; i++)
{
qbeq[1] = frontier[i];
try
{
qp = new QuadraticProgramming(varcov, qg, qaeq, qbeq, qa, qb);
double[] distWeights = qp.GetSolution();
// Найдено оптимальное решение
double tmp = 0.0;
for (int j = 0; j < m; j++) tmp += distWeights[j] * Dot(m, varcov, j, distWeights);
double obj = 0.5 * tmp + Dot(m, qg, distWeights);
solution[i, 0] = System.Math.Sqrt(2.0 * obj); // Доходность портфеля
solution[i, 1] = frontier[i]; // Значение риска
for (int j = 0; j < m; j++) solution[i, j + 2] = distWeights[j]; // Весовые коэффициенты (доли) активов
}
catch (InconsistentSystemException)
{
for (int j = 0; j < m + 2; j++) solution[i, j] = Double.NaN;
}
catch
{
throw;
}
}
}
// Вычисляет скалярное произведение двух векторов
private double Dot(int n, double[] x, double[] y)
{
double sum = 0.0;
for (int k = 0; k < n; k++) sum += x[k] * y[k];
return sum;
}
private double Dot(int n, double[,] x, int index, double[] y)
{
double sum = 0.0;
for (int k = 0; k < n; k++) sum += x[index, k] * y[k];
return sum;
}
// Задает ограничения весовых коэффициентов; m - размер портфеля
public void SetBounds(double[,] b)
{
bw = new double[m + 1, 2];
for (int i = 0; i < m; i++)
{
bw[i, 0] = b[i, 0];
bw[i, 1] = b[i, 1];
}
bw[m, 0] = 1;
bw[m, 1] = 1;
}
// Задает матрицу ковариаций
public void SetCovarianceMatrix(double[,] cov)
{
this.varcov = cov;
}
// Задает ожидаемый результат для каждого элемента портфеля инвестиций
public void SetExpectedReturns(double[] e)
{
this.expectedReturns = e;
}
// Возвращает решение (solution[1][*]), содержащее риск (solution[0][*]) и части портфеля solution[от 2 до 2 + m][*]
public double[,] GetSolution()
{
return Matrix.Transpose(this.solution);
}
}
}