Рассматриваются примеры программирования ансамблей и сборки нейронных сетей (НС), обучаемых классификации данных.
В первом примере ансамбль содержит параллельные ветви, с НС одного или разных видов. В случае НС одного вида ансамбль называется однородным, а разного - гетерогенным [1].
Во втором примере реализуется последовательная сборка двух НС.
В первом примере на вход НС поступают данные разной формы. В общем случае - это массивы, векторы и скаляры. Агрегация входных данных (после преобразований) выполняется слоем Concatenate. Агрегация выходных данных ветвей - слоем Average.
Использованные упрощения моделей обусловлены учебным характером примеров; задача поиска наиболее эффективных моделей НС не рассматривается.
Ансамбли НС в упрощенном виде виде реализуют идею ансамблевого обученния (АО), заключающуюся в обучении нескольких моделей и последующей комбинации их предсказаний [2, 3] (несколько моделей совместно решают одну проблему).
Задача АО - получить из нескольких слабых учеников одного сильного.
Простейшим и далеко не самым эффективным алгоритмом АО является bagging (Bootstrap aggregation, Лео Брейман, 1994), в котором модели обучаются независимо в общем случае на разных выборках одного и того же набора данных. В процессе эксплуатации прогнозы отдельных моделей агрегируются, в результате чего формируется прогноз ансамбля моделей.
Более сложными и эффективными является boosting-алгоритмы (известно несколько такого рода алгоритмов).
Большинство boosting-алгоритмов состоят из итеративного изучения слабых классификаторов относительно распределения и добавления их к окончательному сильному классификатору. Когда они добавляются, они взвешиваются таким образом, чтобы соответствовать точности слабых учеников. После добавления слабого ученика веса данных корректируются, что называется "повторным взвешиванием". Неправильно классифицированные входные данные приобретают больший вес, а примеры, которые классифицированы правильно, теряют вес. Таким образом, будущие слабые ученики больше сосредотачиваются на примерах, которые предыдущие слабые ученики неправильно классифицировали.
В рассматриваемых ниже ансамблях одновременное обучаются все сети ансамбля. Обучение выполняется на одних и тех же выборках. Данные агрегируются в процессе обучения, и ошибка вырабатывается с использованием агрегированных данных. То есть нет независимого обучения моделей. Иными словами, в приводимых примерах идея АО реализуется в упрощенном виде.
В общем случае НС может получать данные разных видов, том числе, и из разных источников. Таким образом, возникает задача слияния данных. Эта задача решается по многим направлениям [4]: Information integration, Data fusion (подмножество Information integration), Sensor fusion, Data integration, Image fusion и Synesthesia.
В приводимых примерах эта задача решается путем создания модели НС с несколькими входами, данные на каждом входе поступают на слой полносвязный Dense (многомерные данные предварительно преобразуются в одномерные, Flatten). Выход Dense-слоев конкатенируется. Объединенные данные поступают на присутствующие в ансамбле сети. В случае сверточной и рекуррентной сети предварительно меняем форму данных (Reshape).
Для агрегации выходов отдельных сетей разработаны многочисленные методы [5]. В том числе, нечеткие (гибридные) НС, такие, как ANFIS и NNFLC. (Агрегация решает проблему "Если сети несогласны". В примерах выходы отдельных сетей агрегируются в результате их усреднения, Average.)
Решается задача классификации объектов, характеризуемых данными разной формы.
Классификация выполняется либо ансамблем нейронных сетей (НС), либо одной НС заданного вида. Из большого числа видов НС [6] в создаваемых ансамблях участвуют сверточные, рекуррентные (LSTM) НС и многослойный перцептрон.
В качества примера берутся объекты, характеризуемые массивом формы (8, 8), двумя векторами, имеющими размеры 10 и 5, и одним скаляром. Скалярная величина представляется в виде вектора единичной длины. Данные с указанными формами подаются на входы сборочной НС или одной НС при отказе от использования ансамбля.
В приводимой ниже программе формы входных данных задаются в списке, определяемым в рассматриваемом ниже примере следующим образом:
inp_shapes_lst = [(8, 8), 10, 5, 1] # Список форм входных данных
Независимо от используемой НС входные данные подвергаются обработке, характер которой иллюстрирует рис. 1.
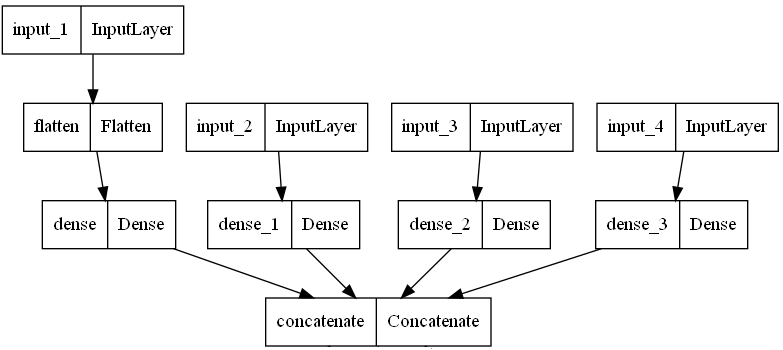
Рис. 1. Этапы обработки входных данных
Многомерные данные (в примере - двумерные) преобразуются в вектор (Flatten). Этот вектор и все прочие одномерные входные данные поступают на соотвествующие полносвязные слои Dense. (Эти слои обучаются.)
Выходы этих слоев объединяются в единый вектор (Concatenate), данные которого используются для формирования входов входящих в ансамбль НС.
Так, перед сверточным слоем вектор преобразуется в одноканальную прямоугольную карту признаков, а перед LSTM - в двумерную карту. Выход слоя Concatenate не требует преобразований, если он подается на слой Dense.
Подготовку данных обеспечивает следующий код:
inp_shapes_lst = [(8, 8), 10, 5, 1] # Список форм входных данных
# Список с числом единиц (нейронов) на Dense-слоях, участвующих в подготовке данных
units_lst = [18, 16, 20, 10]
def inp_layers(inp_shape, units):
inp = KL.Input(inp_shape)
if type(inp_shape) == int:
x = inp
else:
x = KL.Flatten()(inp)
x = KL.Dense(units, activation = 'relu')(x)
return inp, x
def soft_layers(x, units):
x = KL.Dense(units, activation = 'softmax')(x)
return x
inp_lst, x_lst = [], []
for inp_shape, units in zip(inp_shapes_lst, units_lst):
inp, x = inp_layers(inp_shape, units)
inp_lst.append(inp) # Список входных данных
x_lst.append(x) # Список конкатенируемых данных
x = KL.Concatenate()(x_lst)
Модель НС в общем случае может быть ансамблем из сверточных, полносвязных и рекуррентных (LSTM) НС. Составляющие ансамбль НС выполняют параллельную обработку данных (образуют отдельные ветви ансамбля). Каждая ветвь завершается полносвязным слоем с числом единиц, равным числу классов, и с функцией активации Softmax.
Поскольку пример учебный, используются простые НС: в НС каждого вида - сверточной, полносвязной и рекуррентной - содержится по одному слою, отвечающему виду НС, и, как уже сказано, завершающему (классифицирующему) слою Dense.
Выходы разных ветвей усредняются слоем Average. Выход этого слоя является прогнозом модели, принявшей на входе данные разной формы.
Состав модели НС в приводимой ниже программе задается идентификатором из цифр 0, 1 и 2.
Нуль означает ввод в ансамбль ветви из сверточной НС, единица - из рекуррентной (LSTM), а двойка - полносвязной.
Структура ансамбля, заданного идентификатором '012' (гетерогенный ансамбль), показана на рис. 2, а идентификатором '000' (однородный ансамбль) - на рис. 3.
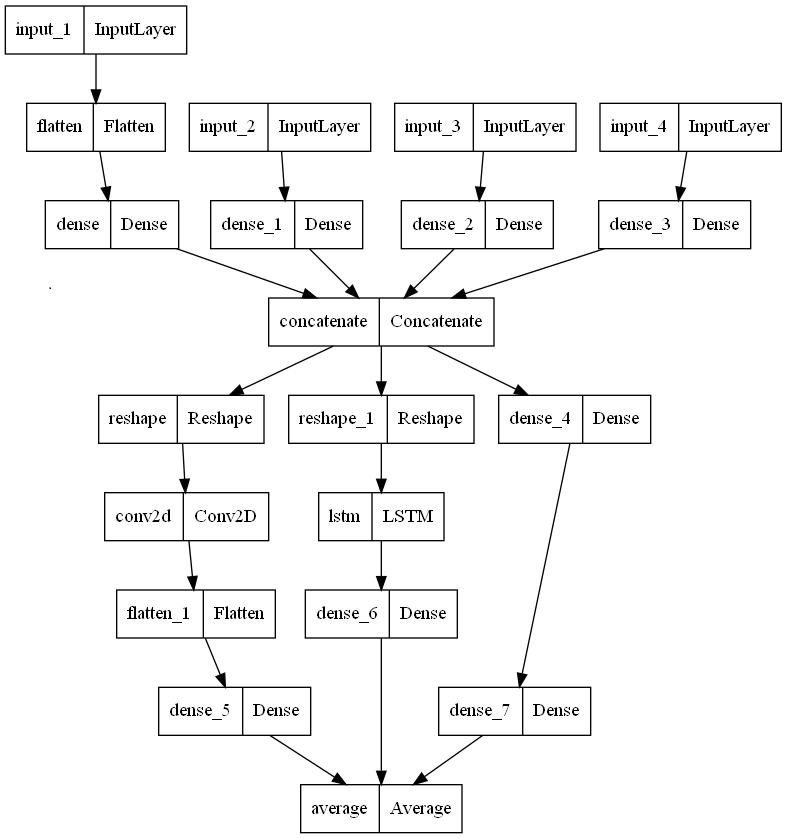
Рис. 2. Модель '012' - гетерогенная
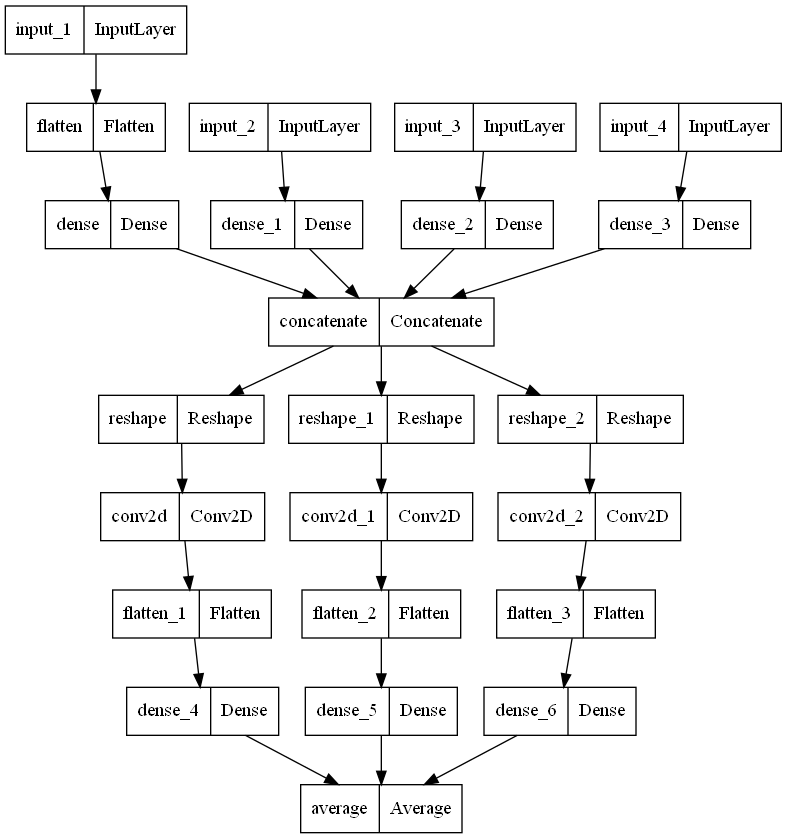
Рис. 3. Модель '000' - однородная
Число и состав ветвей в ансамбле произвольно.
Создание модели НС обеспечивает следующий код:
def make_model(inp_shapes_lst, units_lst, num_classes, n_nn):
def inp_layers(inp_shape, units):
inp = KL.Input(inp_shape)
if type(inp_shape) == int:
x = inp
else:
x = KL.Flatten()(inp)
x = KL.Dense(units, activation = 'relu')(x)
return inp, x
def soft_layers(x, units):
x = KL.Dense(units, activation = 'softmax')(x)
return x
inp_lst, x_lst = [], []
for inp_shape, units in zip(inp_shapes_lst, units_lst):
inp, x = inp_layers(inp_shape, units)
inp_lst.append(inp) # Список входных данных
x_lst.append(x) # Список конкатенируемых данных
x = KL.Concatenate()(x_lst)
xn_lst, xs_lst = [], []
for k in n_nn:
if k == '0': # CNN
x2 = KL.Reshape((s2, s2, 1))(x)
x2 = KL.Conv2D(4, 2, activation = 'relu', padding = 'same')(x2)
x2 = KL.Flatten()(x2)
if k == '1': # RNN
x2 = KL.Reshape((s2, s2))(x)
x2 = KL.LSTM(8)(x2)
if k == '2': # MLP
x2 = KL.Dense(16, activation = 'relu')(x)
xn_lst.append(x2)
for x in xn_lst:
xs_lst.append(soft_layers(x, num_classes))
if len(n_nn) == 1:
out = xs_lst[0]
else:
out = KL.Average()(xs_lst)
model = Model(inp_lst, out)
if n_nn == mdl_to_plt:
if show_model:
model.summary()
if plt_model:
from tensorflow.keras.utils import plot_model
plot_model(model, to_file = 'nn_graph.png')
model.compile(loss = 'mse', optimizer = 'adam', metrics = 'accuracy')
return model
#
inp_shapes_lst = [(8, 8), 10, 5, 1] # Список форм входных данных
# Список с числом единиц (нейронов) на Dense-слоях, участвующих в подготовке данных
units_lst = [18, 16, 20, 10]
num_classes = 4
s = sum(units_lst)
s2 = int(np.sqrt(s))
assert s == s2 * s2
assert len(inp_shapes_lst[0]) == 2
n_nn = '012'
model = make_model(inp_shapes_lst, units_lst, num_classes, n_nn)
Проверка работоспособности модели выполняется на случайно сгенерированном наборе данных.
В набор попадают по n примеров каждого вида (n = 300, например).
Так, при задании
inp_shapes_lst = [(8, 8), 10, 5, 1] # Список форм входных данных
В наборе окажутся n массивов формы (8, 8), n векторов длины 5 и так далее.
Каждый пример, снабжается меткой - целым числом из отрезка [0 - (число_классов - 1)]. Метка назначается случайно.
Генерацию данных обеспечивает следующий код:
def make_data(inp_shapes_lst, num_classes, n = 200):
all_x = []
for inp_shape in inp_shapes_lst:
if type(inp_shape) == int:
x = np.random.rand(n, inp_shape)
else:
d0 = inp_shape[0]
d1 = inp_shape[1]
x = np.random.rand(n, d0, d1)
all_x.append(x)
y = np.random.randint(0, num_classes, size = n)
y = tf.keras.utils.to_categorical(y, num_classes)
return all_x, y
#
inp_shapes_lst = [(8, 8), 10, 5, 1] # Список форм входных данных
num_classes = 4
x, y = make_data(inp_shapes_lst, num_classes, n = 300)
Поскольку пример учебный, то для упрощения проверки работоспособности модели данные не делятся на обучающее, оценочное и проверочное множества, а целиком используются для обучения, которое активизируется методом fit:
score = model.fit(x, y, batch_size = 32, epochs = 100, verbose = 0)
Результаты обученния моделей, заданных списком ['012', '01', '02', '12', '0', '1', '2', '000', '111', '222'] (последовательно создается и обучается каждая модель списка):
0 - CNN; 1 - RNN; 2 - MLP
Модель 012: loss = 0.0793; accuracy = 82.67
Модель 01: loss = 0.0843; accuracy = 82.67
Модель 02: loss = 0.0609; accuracy = 89.67
Модель 12: loss = 0.0769; accuracy = 81.67
Модель 0: loss = 0.0732; accuracy = 82.33
Модель 1: loss = 0.095; accuracy = 74.67
Модель 2: loss = 0.0684; accuracy = 85.33
Модель 000: loss = 0.0766; accuracy = 84.33
Модель 111: loss = 0.0908; accuracy = 79.0
Модель 222: loss = 0.0603; accuracy = 86.67
Какие-либо суждения о качестве (эффективности) моделей можно будет сделать при работе с реальными данными по результатам тестирования обученной модели.
Как показывает опыт [7], модели, эффективные на одном наборе данных, показывают скромные, уступающие другим моделям результаты на другом наборе данных.
Число и виды сборок задаются списком models_lst, содержащим идентификаторы моделей, например:
models_lst = ['012', '01', '02', '12', '0', '1', '2', '000', '111', '222']
Флажки show_model и plt_model задают/отменяют соответственно печать сведений о слоях модели (model.summary()) и рисунка и запись структуры модели НС в файл nn_graph.png. Сведения и рисунок выводятся для модели с идентификаторм, хранимым переменной mdl_to_plt, например, mdl_to_plt = '000' Весь код:
import numpy as np
from tensorflow.keras.models import Model
import tensorflow.keras.layers as KL
import tensorflow as tf
# 0 - CNN
# 1 - RNN
# 2 - MLP
show_model = False
plt_model = False
mdl_to_plt = '000' # Идентификатор модели, структура которой выводится на печать и сохраняется в файле
seed = 2
np.random.seed(seed)
tf.random.set_seed(seed)
inp_shapes_lst = [(8, 8), 10, 5, 1] # Список форм входных данных
# Список с числом единиц (нейронов) на Dense-слоях, участвующих в подготовке данных
units_lst = [18, 16, 20, 10]
num_classes = 4
s = sum(units_lst)
s2 = int(np.sqrt(s))
assert s == s2 * s2
assert len(inp_shapes_lst[0]) == 2
# def make_data(inp_shapes_lst, num_classes, n = 200):
all_x = []
for inp_shape in inp_shapes_lst:
if type(inp_shape) == int:
x = np.random.rand(n, inp_shape)
else:
d0 = inp_shape[0]
d1 = inp_shape[1]
x = np.random.rand(n, d0, d1)
all_x.append(x)
y = np.random.randint(0, num_classes, size = n)
y = tf.keras.utils.to_categorical(y, num_classes)
return all_x, y
def make_model(inp_shapes_lst, units_lst, num_classes, n_nn):
def inp_layers(inp_shape, units):
inp = KL.Input(inp_shape)
if type(inp_shape) == int:
x = inp
else:
x = KL.Flatten()(inp)
x = KL.Dense(units, activation = 'relu')(x)
return inp, x
def soft_layers(x, units):
x = KL.Dense(units, activation = 'softmax')(x)
return x
inp_lst, x_lst = [], []
for inp_shape, units in zip(inp_shapes_lst, units_lst):
inp, x = inp_layers(inp_shape, units)
inp_lst.append(inp) # Список входных данных
x_lst.append(x) # Список конкатенируемых данных
x = KL.Concatenate()(x_lst)
xn_lst, xs_lst = [], []
for k in n_nn:
if k == '0': # CNN
x2 = KL.Reshape((s2, s2, 1))(x)
x2 = KL.Conv2D(4, 2, activation = 'relu', padding = 'same')(x2)
x2 = KL.Flatten()(x2)
if k == '1': # RNN
x2 = KL.Reshape((s2, s2))(x)
x2 = KL.LSTM(8)(x2)
if k == '2': # MLP
x2 = KL.Dense(16, activation = 'relu')(x)
xn_lst.append(x2)
for x in xn_lst:
xs_lst.append(soft_layers(x, num_classes))
if len(n_nn) == 1:
out = xs_lst[0]
else:
out = KL.Average()(xs_lst)
model = Model(inp_lst, out)
if n_nn == mdl_to_plt:
if show_model:
model.summary()
if plt_model:
from tensorflow.keras.utils import plot_model
plot_model(model, to_file = 'nn_graph.png')
model.compile(loss = 'mse', optimizer = 'adam', metrics = 'accuracy')
return model
#
print('Готовим данные')
x, y = make_data(inp_shapes_lst, num_classes, n = 300)
print('0 - CNN; 1 - RNN; 2 - MLP')
models_lst = ['012', '01', '02', '12', '0', '1', '2', '000', '111', '222']
for n_nn in models_lst:
model = make_model(inp_shapes_lst, units_lst, num_classes, n_nn)
score = model.fit(x, y, batch_size = 32, epochs = 100, verbose = 0)
lss = round(score.history['loss'][-1], 4)
acc = 100 * round(score.history['accuracy'][-1], 4)
print('Модель:', n_nn, 'loss =', lss, 'accuracy =', acc)
print('Готово')
Рассматривается пример создания сборки двух нейронных сетей (НС).
Сборка решает ранее рассмотренную задачу классификации графиков элементарных функций и простых геометрических фигур.
Структура последовательной сборки показана на рис. 4.
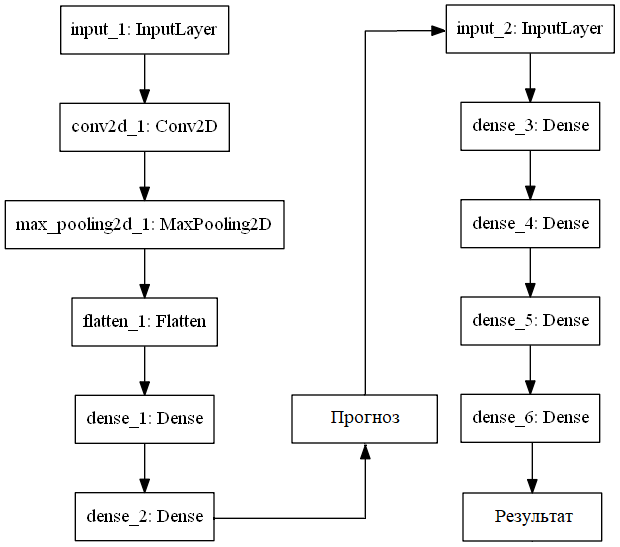
Рис. 4. Структура последовательного ансамбля двух нейронных сетей
Структура каждой НС воспроизводится в результате выполнения следующего кода:
from tensorflow.keras.utils import plot_model
plot_model(model, to_file = 'nn_graph.png')
Первая сеть является сверточной, вторая - многослойным перцептроном.
Описание структур сетей выводится в результате выполнения
model.summary()
Описание структуры первой сети:
Layer (type) Output Shape Param #
==================================================
input_1 (InputLayer) (None, 64, 64, 1) 0
________________________________________________________
conv2d_1 (Conv2D) (None, 64, 64, 2) 34
________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 8, 8, 2) 0
________________________________________________________
flatten_1 (Flatten) (None, 128) 0
________________________________________________________
dense_1 (Dense) (None, 16) 2064
________________________________________________________
dense_2 (Dense) (None, 6) 102
==================================================
Total params: 2,200
Trainable params: 2,200
Non-trainable params: 0
Описание структуры второй сети:
Layer (type) Output Shape Param #
=================================================
input_2 (InputLayer) (None, 6) 0
_______________________________________________________
dense_3 (Dense) (None, 16) 112
_______________________________________________________
dense_4 (Dense) (None, 48) 816
_______________________________________________________
dense_5 (Dense) (None, 12) 588
_______________________________________________________
dense_6 (Dense) (None, 6) 78
=================================================
Total params: 1,594
Trainable params: 1,594
Non-trainable params: 0
Классифицируемые изображения записаны в двоичные файлы dataTrain.bin, labelsTrain.bin, dataTest.bin, labelsTest.bin, содержащие соответственно обучающие и тестовые данные.
Файлы data* содержат сведения об изображениях, а файлы labels* – соответствующие им метки (табл. 1).
Таблица 1. Классы изображений и их метки
| Класс | Метка |
|---|---|
| Часть параболы | 0 |
| Парабола | 1 |
| Часть экспоненты | 2 |
| Экспонента | 3 |
| Прямоугольник без одной стороны | 4 |
| Прямоугольник | 5 |
Фактически метка – это номер класса.
Все изображения выполнены в оттенках серого цвета на площадке размером 64*64 пикселя.
Каждый пиксель содержит число в диапазоне [0, 255].
Всего в файле с обучающими данными находятся сведения о 600-х изображениях, а в файле с тестовыми данными – о 150-и.
Выход первой и соответственно вход второй сети формируется следующим кодом:
# Выход первой сети
print('Подготовка входа второй сети (обучающие и тестовые данные)')
train_pred = model.predict(train_data, batch_size = 1)
test_pred = model.predict(test_data, batch_size = 1)
Тип выхода покажет следующая печать:
print(type(test_pred)) # <class 'numpy.ndarray'>
Несколько элементов на выходе первой сети (печатается test_pred):
[[ 4.16896820e-01 1.31221205e-01 5.70299029e-01 4.62679490e-02 8.79633874e-02 1.51358783e-01]
[ 5.18408954e-01 7.38345161e-02 6.20221198e-01 1.20329976e-01 1.03515081e-01 1.17906049e-01] ...]
Выделенные элементы показывают, как первая сеть классифицирует образы. Она отнесла их ко второму классу, что соответствует действительности.
import numpy as np
import sys # Для sys.exit()
import matplotlib.pyplot as plt
import time
import keras
from keras.utils import plot_model
from keras.models import Model
from keras.layers import Input, Dense, Flatten
from keras.layers import Conv1D, Conv2D, MaxPooling1D, MaxPooling2D
from keras import backend as K
from keras import optimizers
#
# Пользовательская функция потерь. На входе тензоры
def myLoss(y_true, y_pred):
dist = K.sqrt(K.sqrt(K.sum(K.square(K.square(y_pred - y_true)))))
err = dist
return err # Вернет тензор с shape = (?, )
#
def loadData(fn, fn2):
with open(fn, 'rb') as read_binary:
data = np.fromfile(read_binary, dtype = np.int16)
with open(fn2, 'rb') as read_binary:
labels = np.fromfile(read_binary, dtype = np.int16)
return data, labels
#
np.random.seed(348)
fn_train, fn_train_labels = 'dataTrain.bin', 'labelsTrain.bin'
fn_test, fn_test_labels = 'dataTest.bin', 'labelsTest.bin'
num_classes = 6 # Число классов
w, h = 64, 64 # Ширина и высота окна вывода рисунка
categorical = True
#
print('Число классов: ' + str(num_classes))
train_data, train_labels = loadData(fn_train, fn_train_labels)
test_data, test_labels = loadData(fn_test, fn_test_labels)
n_train = int(train_data.size / (w * h)) # Число рисунков для обучения
n_test = int(test_data.size / (w * h)) # Число тестовых рисунков
#
train_data, test_data = train_data.reshape(n_train, w, h, 1), test_data.reshape(n_test, w, h, 1)
train_data, test_data = train_data.astype('float32'), test_data.astype('float32')
train_data /= 255
test_data /= 255
test_labels_0 = test_labels # Для сравнения с результатами прогноза
if categorical:
train_labels = keras.utils.to_categorical(train_labels, num_classes)
test_labels = keras.utils.to_categorical(test_labels, num_classes)
#
print(train_data.shape[0], 'обучающих образов')
print(test_data.shape[0], 'тестовых образов')
#
visible = Input(shape = (w, h, 1))
hidden1 = Conv2D(2, kernel_size = (4, 4), strides = (1, 1), padding = 'same', activation = 'relu')(visible)
hidden2 = MaxPooling2D(pool_size = (8, 8), strides = (8, 8), padding = 'same')(hidden1)
hidden3 = Flatten()(hidden2)
hidden4 = Dense(16, activation = 'relu')(hidden3)
output = Dense(num_classes, activation = 'linear')(hidden4)
model = Model(inputs = visible, outputs = output)
model.compile(loss = myLoss, optimizer = 'adam', metrics = ['accuracy'])
##model.summary()
##plot_model(model, to_file = 'nn_graph.png')
#
cnn = False
if cnn:
visible2 = Input(shape = (num_classes, 1))
hidden2_1 = Conv1D(1, kernel_size = 4, activation = 'relu')(visible2)
hidden2_2 = MaxPooling1D(pool_size = 2)(hidden2_1)
hidden2_3 = Flatten()(hidden2_2)
hidden2_4 = Dense(16, activation = 'relu')(hidden2_3)
output2 = Dense(num_classes, activation = 'softmax')(hidden2_4) # softmax, sigmoid
else:
visible2 = Input(shape = (num_classes, ))
hidden2_1 = Dense(16, activation = 'linear')(visible2)
hidden2_2 = Dense(48, activation = 'linear')(hidden2_1)
hidden2_3 = Dense(12, activation = 'linear')(hidden2_2)
output2 = Dense(num_classes, activation = 'softmax')(hidden2_3)
model2 = Model(inputs = visible2, outputs = output2)
model2.compile(loss = myLoss, optimizer = 'adam', metrics = ['accuracy'])
##model2.summary()
##plot_model(model2, to_file = 'mlp_graph.png')
#
# Обучение
print('\nОбучение 1')
start_time = time.time()
model.fit(train_data, train_labels, batch_size = 10, epochs = 5, verbose = 2)
print('Время обучения 1: ', (time.time() - start_time))
#
print('Тестирование 1')
score = model.evaluate(test_data, test_labels, verbose = 0)
print('Потери при тестировании 1: ', score[0])
print('Точность при тестировании 1:', score[1])
#
# Выход первой сети
print('\nПодготовка входа второй сети (обучающие и тестовые данные)')
train_pred = model.predict(train_data, batch_size = 10)
test_pred = model.predict(test_data, batch_size = 10)
if cnn:
dim0, dim1 = train_pred.shape[0], train_pred.shape[1]
train_pred = train_pred.reshape(dim0, dim1, 1)
dim0, dim1 = test_pred.shape[0], test_pred.shape[1]
test_pred = test_pred.reshape(dim0, dim1, 1)
#
print('\nОбучение 2')
start_time = time.time()
model2.fit(train_pred, train_labels, batch_size = 10, epochs = 5, verbose = 0)
print('Время обучения 2: ', (time.time() - start_time))
#
print('Тестирование 2')
score2 = model2.evaluate(test_pred, test_labels, verbose = 0)
print('Потери при тестировании 2: ', score2[0])
print('Точность при тестировании 2:', score2[1])
#
print("Прогноз")
test_pred2 = model2.predict(test_pred) # , batch_size = 10
# Формируем массив предсказанных классов
classes = np.zeros(n_test, dtype = np.int)
k = - 1
for pred in test_pred2:
k += 1
classes[k] = np.argmax(pred)
# np.sum(classes == test_labels) вернет сумму случаев, когда classes[i] = test_labels[i]
acc = np.sum(classes == test_labels_0) / n_test * 100
print(classes)
print("На самом деле:")
print(test_labels_0)
print("Точность прогнозирования: " + str(acc) + '%')
if acc < 100:
show = True
for i in range(n_test):
if classes[i] != test_labels_0[i]:
print('i = ' + str(i) + '. Прогноз: ' + str(classes[i]) + '. На самом деле: ' + str(test_labels_0[i]))
if show:
show = False
plt.subplot()
plt.imshow(test_data[i].reshape(w, h), cmap = plt.get_cmap('gray'))
plt.show()
Выводятся следующие сведения:
Число классов: 6
600 обучающих образов
150 тестовых образов
Обучение 1
Время обучения 1: 12.615854740142822
Тестирование 1
Потери при тестировании 1: 0.9830639735857646
Точность при тестировании 1: 0.9866666666666667
Подготовка входа второй сети (обучающие и тестовые данные)
Обучение 2
Время обучения 2: 1.8649725914001465
Тестирование 2
Потери при тестировании 2: 0.41069
Точность при тестировании 2: 0.9933
В рассматриваемой задаче две сети работают хуже, чем одна: одни образ оказался нераспознанным. Он показан на рис. 5.
Рис. 5. Нераспознанный образ
Не решает проблемы и использование дополнительного LeakyReLU-слоя [1]: по-прежнему один образ остается нераспознанным.
Добавление LeakyReLU становится возможным после его импортирования:
from keras.layers import LeakyReLU
Тогда модель второй сети можно записать следующим образом:
visible2 = Input(shape = (num_classes, ))
hidden2_1 = Dense(16, activation = 'linear')(visible2)
hidden2_2 = Dense(48, activation = 'linear')(hidden2_1)
hidden2_3 = Dense(12)(hidden2_2)
hidden2_4 = LeakyReLU(alpha = 0.4) (hidden2_3)
output2 = Dense(num_classes, activation = 'softmax')(hidden2_4)
Вторая сеть сохраняет 100% классификацию, если первая сеть распознала все образы (это получается при усложнении структуры первой сети).
Если же первая сеть не справляется с классификацией, то вторая сеть, улучшая результат, так же не достигает 100% результата.
В то же время одновременное применение двух и более сетей для решения задачи предоставляет следующие дополнительные возможности. Вот некоторые из них:
1. Глубокие нейросети (часть VI). Ансамбль нейросетевых классификаторов: bagging. [Электронный ресурс] URL: https://www.mql5.com/ru/articles/4227#ensembles
2. Sewell M. Ensemble Learning. - 2007. - 16 c. [Электронный ресурс] URL: http://www.machine-learning.martinsewell.com/ensembles/ensemble-learning.pdf.
3. Ensemble Machine Learning. Methods and Applications. Editors: Cha Zhang, Yunqian Ma. - Springer New York Dordrecht Heidelberg London, 2012. - 329 с.
4. Information integration. [Электронный ресурс] URL: https://en.wikipedia.org/wiki/Information_integration.
5. Нечеткие нейронные сети. [Электронный ресурс] URL: https://studbooks.net/1783599/informatika/nechetkie_neyronnye_seti.
6. Fjodor V.V. The neural network zoo. [Электронный ресурс] URL: https://www.asimovinstitute.org/neural-network-zoo/
7. Классификация изображений нейронной сетью. [Электронный ресурс] URL: http://www.100byte.ru/python/imgClasses/imgClasses.html
8. Keras. Advanced activations. [Электронный ресурс] URL: https://keras.io/layers/advanced-activations/.