Нейронная сеть (НС), решающая, болен человек сахарным диабетом или нет, реализуется на Питоне с применением библиотеки TensorFlow с оболочкой Keras. Вывод графиков потерь и точности осуществлен средствами matplotlib.
Установка TensorFlow, Keras и прочих библиотек выполняется в командном окне, которое в Windows открывается после нажатия Win + X.
Установка обычной или GPU-версий Tensorflow [1]:
<path>/Scripts/pip install --upgrade tensorflow
<path>/Scripts/pip install --upgrade tensorflow-gpu
Например, установка matplotlib:
C:/Users/HP/AppData/Local/Programs/Python/Python36/Scripts/pip install matplotlib
Установка обычной и GPU-версий Keras:
<path>/Scripts/pip install keras
Обучение проводится по следующим данным:
Примеры данных приведены на рис. 1.
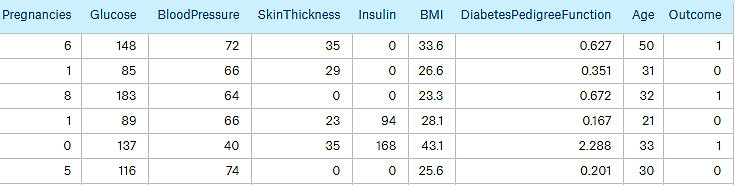
Рис. 1. Диагностические данные
Всего в таблице 768 строк. Данные разбиваются на две части: обучающую и для тестирования. Каждая часть, в свою очередь, разбивается на матрицу с данными и вектор с выходными данными (последний столбец исходной таблицы). В обучающую выборку (массивы trainData и trainOutput) включаются первые 3/4 строк исходной таблицы, последующие строки попадают в выборку для проверки сети (массивы testData и testOutput).
Данные находятся в csv-файле и описаны в [2]. В качестве разделителя используется точка с запятой.
Взята полносвязная нейронная сеть (НС) с тремя скрытыми слоями. Структура сети приведена в табл. 1:
Таблица 1. Структура НС
| Слой | Функция активации | Число нейронов |
|---|---|---|
| Входной | 7 | |
| Первый скрытый слой | ReLU | 16 |
| Второй скрытый слой | Та же | 32 |
| Третий скрытый слой | Та же | 16 |
| Выходной | Sigmoid | 1 |
Графики функций активации ReLU и Sigmoid показаны на рис. 2.
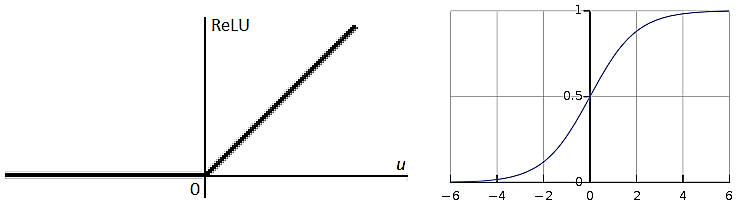
Рис. 2. Функции активации ReLU и Sigmoid
На рис. 3 показаны схема перцептрона (для иллюстрации идеи архитектуры НС), архитектура полносвязной НС с одним скрытым слоем и пороговая функция перцептрона.
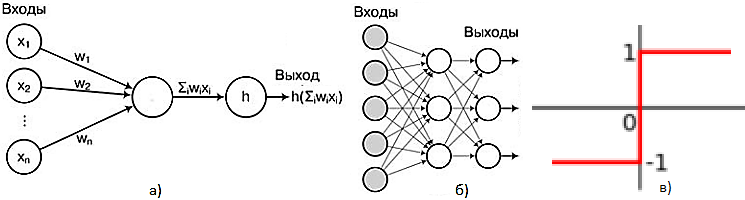
Рис. 3. Архитектура полносвязной НС: а – перцептрон; б – полносвязная НС; в – пороговая функция перцептрона
Перцептрон (рис. 3, а) обеспечивает бинарную классификацию – объект будет отнесен перцептроном к одному из двух классов; h – пороговая функция (рис. 3, в).
Схема обучения классификатора показана на рис. 4.
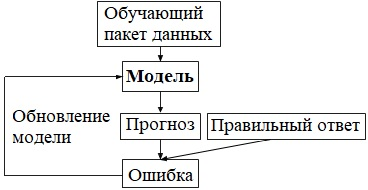
Рис. 4. Схема обучения классификатора
Перцептрон можно рассматривать как модель искусственного нейрона, построенную по аналогии с моделью биологического нейрона (рис. 5).
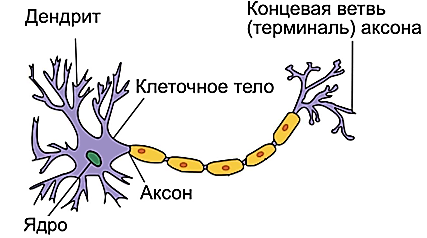
Рис. 5. Модель биологического нейрона
Биологический нейрон передает информацию с помощью электрических и химических сигналов. Нейрон состоит из тела нейрона и отростков: дендритов и аксона, которые связывают нейроны в нейронную сеть. Дендриты отвечают за приём сигналов от других нейронов, а аксон – за передачу сигналов. Аксон заканчивается концевой ветвью (терминалью), которая образует с дендритами другого нейрона соединение – синапс. Синапс способен менять форму при изменении разности потенциалов. Изменение формы влияет на силу передачи сигналов. Выход нейрона распределяется по многим синапсам на множество нейронов и наоборот на данный нейрон сходятся синапсы от множества источников [3].
Дендритами искусственного нейрона являются его связи с другими нейронами или входными данными, которые выражаются в числовом векторе w1, w2, …, wn, называемым вектором весов. Он определяет силу синаптической связи с другими нейронами или входными данными.
# Реализуется многослойный перцептрон
import numpy as np
import sys, os, numpy, keras
import matplotlib.pyplot as plt
from tkinter import messagebox # Вывод сообщений
from keras.models import Sequential # Линейный стек слоев
from keras.layers import Dense # Добавление полносвязного слоя
from keras import optimizers
from numpy import array
from sklearn.preprocessing import StandardScaler # Стандартизация данных
#
class LossHistory(keras.callbacks.Callback):
def on_train_begin(self, logs = {}):
self.losses = [] # Потери и точность
self.acc = []
self.val_loss = []
self.val_acc = []
#
def on_epoch_end(self, batch, logs = {}):
self.val_loss.append(logs.get('val_loss'))
self.val_acc.append(logs.get('val_acc'))
#
def on_batch_end(self, batch, logs = {}):
self.losses.append(logs.get('loss'))
self.acc.append(logs.get('acc'))
#
# Задание затравки датчика случайных чисел обеспечит повторяемость результата
np.random.seed(348)
#
file = "G:/python/SimpleNN/pima_indians_diabetes.csv"
if os.path.exists(file):
print ("Файл найден")
else:
print ("Файл не найден")
exit()
# Задание затравки датчика случайных чисел обеспечит повторяемость результата
numpy.random.seed(348)
# Загружаем диагностические данные для обучения сети
# Файл с данными - это таблица из 8-ми столбцов; в последнем стобце 0, если нет диабета, или 1 - в противном случае
allData = numpy.loadtxt(file, delimiter = ";") # allData[0, 0]) - первый элемент матрицы
allDataLen = len(allData[:, 0])
print(allDataLen) # 768
X = allData[:,0:8]
y = allData[:,8]
##print(X)
#
# fit- вычисляет среднее значение и стандартное отклонение для последующей стандартизации
scaler = StandardScaler(copy = False).fit(X)
X = scaler.transform(X) # Стандартизация за счет центрирования и масштабирования
#
##print(X)
##sys.exit()
# X_train - матрица параметров (диагностические данные, первые 8 столбцов в табл. рис. 1);
# y_train - выход сети (0 или 1, см. последний столбец в табл. на рис. 1)
# Размер порция тренировочных данные (обучающей данных)
X_trainLen = int(3 * allDataLen / 4)
# Тренировочные и проверочные данные
X_train, y_train = X[0:X_trainLen, 0:8], y[0:X_trainLen]
X_test, y_test = X[X_trainLen + 1:, 0:8], y[X_trainLen + 1:]
##print(X_test)
##print(y_test)
##sys.exit()
categorical = False # True, False
if categorical:
num_classes = 2
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
lossFun = 'categorical_crossentropy'
else:
num_classes = 1
lossFun = 'mean_squared_error'
#
# Виды функцции потерь:
# mean_squared_error; mean_absolute_error; mean_absolute_percentage_error
# mean_squared_logarithmic_error; squared_hinge; hinge;
# categorical_hinge; logcosh; categorical_crossentropy;
# sparse_categorical_crossentropy; binary_crossentropy;
# kullback_leibler_divergence; cosine_proximity
#
# Виды методов оптимизации:
# SGD; RMSprop; Adagrad; Adadelta; Adam; Adamax; Nadam; TFOptimizer
# Вариант задания метода оптимизации
# optKind = optimizers.SGD(lr = 0.01, decay = 1e-6, momentum = 0.9, nesterov = True)
#
# Создаем НС
model = Sequential()
# Для входного слоя необходимо указать input_dim - число входов
# 12 - число выходов первого слоя
# relu - функция активации нейрона
actFun = 'relu'
actFun2 = 'sigmoid' # softmax, sigmoid
model.add(Dense(16, input_dim = 8, activation = actFun))
# 32 - число выходов второго слоя; число входов равно числу выходов предшествующего слоя
model.add(Dense(48, activation = actFun))
##model.add(Dense(16, activation = actFun))
# sigmoid - функция активация нейрона последнего слоя
model.add(Dense(num_classes, activation = actFun2))
# Компиляция НС с функцией потерь lossFun и алгоритма Adam ее минимизации (обновляются веса НС)
optKind = 'Adam'
model.compile(loss = lossFun, optimizer = optKind, metrics = ['accuracy'])
#
# Обучение нейронной сети
print('\nОбучение')
# epochs - число обучающих эпох
# batch_size - параметр, определяющий форму входного массива
# В случае 2D (это наш случай), на входе сети будет массив формы (batch_size, input_dim)
allPoints = True # True or False
if allPoints:
# CallBack
history = LossHistory()
model.fit(X_train, y_train, epochs = 10, batch_size = 30, verbose = 2, callbacks = [history])
else:
# Получаем историю после завершения эпохи
history = model.fit(X_train, y_train, epochs = 6, batch_size = 30, verbose = 2)
#
# Оценка результата
print('\nТестирование')
scores = model.evaluate(X_test, y_test, verbose = 2)
#scores = model.evaluate(X_train, y_train)
#
print("%s: %.2f%%" % (model.metrics_names[0], scores[0]*100)) # loss (потери)
print("%s: %.2f%%" % (model.metrics_names[1], scores[1]*100)) # acc (точность)
#
predictions = model.predict(X_test)
rounded = [round(x[0]) for x in predictions]
print('Прогноз:')
print(rounded)
#
# messagebox.showinfo(title = "Done", message = "Готово")
#
print('Потери и точность на каждой эпохе')
if allPoints:
print(history.val_loss)
print(history.val_acc)
else:
print(history.history['val_loss'])
print(history.history['val_acc'])
#
# Графики изменения потерь и точности в процессе обучения
if allPoints:
#print(history.losses)
cnt = len(history.losses)
else:
cnt = len(history.history['loss'])
rng = numpy.arange(cnt)
#
# Вариант 1 вывода графиков потерь и точности
fig, ax = plt.subplots(figsize = (8, 4))
if allPoints:
ax.scatter(rng, history.losses, marker = 'o', c = 'red', edgecolor = 'black', label = 'Потери')
ax.scatter(rng, history.acc, marker = 'o', c = 'blue', edgecolor = 'black', label = 'Точность')
else:
ax.scatter(rng, history.history['loss'], marker = 'o', c = 'red', edgecolor = 'black', label = 'Потери')
ax.scatter(rng, history.history['acc'], marker = 'o', c = 'blue', edgecolor = 'black', label = 'Точность')
ax.set_title('Потери и Точность в процессе обучения')
ax.legend(loc = 'upper left')
ax.set_ylabel('Потери, Точность')
ax.set_xlabel('Шаг')
ax.set_xlim([0, cnt])
ax.set_ylim([0, 1])
fig.show()
#
# Другой вариант вывода графиков потерь и точности
"""
plt.title('Потери и Точность в процессе обучения')
if allPoints:
plt.scatter(rng, history.losses, marker = 'o', c = 'red', edgecolor = 'black', label = 'Потери')
plt.scatter(rng, history.acc, marker = 'o', c = 'blue', edgecolor = 'black', label = 'Точность')
else:
plt.scatter(rng, history.history['loss'], marker = 'o', c = 'red', edgecolor = 'black', label = 'Потери')
plt.scatter(rng, history.history['acc'], marker = 'o', c = 'blue', edgecolor = 'black', label = 'Точность')
plt.legend(loc = 'upper left')
plt.xlim([0, cnt])
plt.ylim([0, 1])
plt.ylabel('Потери, Точность')
plt.xlabel('Шаг')
plt.show()
"""
По ходу обучения выводятся следующие сведения:
Using TensorFlow backend.
Файл найден
768
Обучение
Epoch 1/10
- 1s - loss: 0.2506 - acc: 0.5122
Epoch 2/10
- 0s - loss: 0.2241 - acc: 0.7153
Epoch 3/10
- 0s - loss: 0.2075 - acc: 0.7326
Epoch 4/10
- 0s - loss: 0.1941 - acc: 0.7344
Epoch 5/10
- 0s - loss: 0.1853 - acc: 0.7396
Epoch 6/10
- 0s - loss: 0.1793 - acc: 0.7465
Epoch 7/10
- 0s - loss: 0.1744 - acc: 0.7535
Epoch 8/10
- 0s - loss: 0.1709 - acc: 0.7517
Epoch 9/10
- 0s - loss: 0.1671 - acc: 0.7569
Epoch 10/10
- 0s - loss: 0.1642 - acc: 0.7674
Тестирование
loss: 16.14%
acc: 76.44%
Прогноз:
[0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, ...]
При отсутствии стандартизации данных результаты будут хуже:
loss: 36.65%
acc: 63.35%
Потери и точность на каждом шаге обучения показаны на рис. 6 и 7.
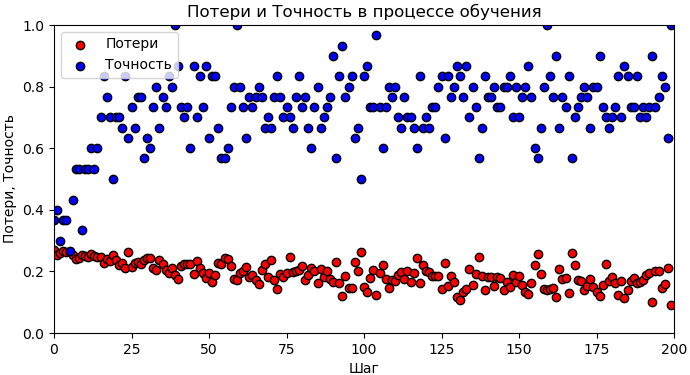
Рис. 6. Графики изменения потерь и точности на этапе обучения сети (выполнена стандартизации данных)
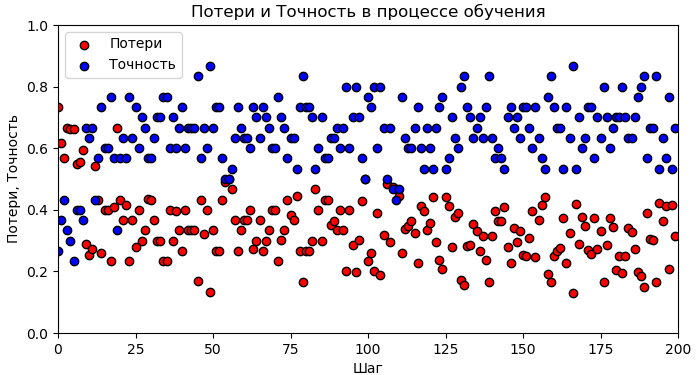
Рис. 7. Графики изменения потерь и точности на этапе обучения сети (нет стандартизации данных)
Для вывода графиков потерь и точности, иллюстрирующих процесс обучения, создан класс LossHistory.
Экземпляр history этого класса использован в качестве callBack-параметра метода model.fit.
Свойства losses и acc рассматриваемого класса являются массивами, в которых накапливаются потери и точность, вычисляемые в процессе обучения, продолжительность которого определяется параметром batch_size.
Подготовку данных обеспечит следующий код:
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
data = np.loadtxt('diab.csv', delimiter = ',') # 768 примеров
x = data[:, 0:8]
y = data[:, 8]
scaler = StandardScaler(copy = False).fit(x)
x = scaler.transform(x)
# Получаем обучающее и проверочнное множества
x_trn, x_tst, y_trn, y_tst = train_test_split(x, y, test_size = 0.2, random_state = 22)
y_tst0 = y_tst.copy() # Для оценки результатов обучения
y_trn = keras.utils.to_categorical(y_trn, num_classes)
y_tst = keras.utils.to_categorical(y_tst, num_classes)
last_activation = 'softmax'
# Задаем несвязанные слои для употребления с GradientTape
inp = layers.Input(shape = (len(x_trn[0]), ))
h = layers.Dense(32, activation = 'relu')
h2 = layers.Dense(16, activation = 'relu')
out = layers.Dense(num_classes, activation = last_activation)
# Создание модели НС
y = h(inp)
y = h2(y)
model = keras.Model(inputs = inp, outputs = out(y))
Оптимизатор:
optimizer = keras.optimizers.Adam(learning_rate = 0.01)
Компиляция модели:
model.compile(loss = 'mse', optimizer = optimizer, metrics = ['accuracy'])
Чуть выше обучение НС запускал метод fit:
epochs = 20
model.fit(x_trn, y_trn, epochs = epochs, batch_size = batch_size, verbose = 0)
Альтернативой является обучение на пакетах с методом train_on_batch.
Пакеты можно сформировать, следующим образом:
batch_size = 32 # Число примеров в пакете
dataset = tf.data.Dataset.from_tensor_slices((x_trn, y_trn))
dataset = dataset.batch(batch_size)
Цикл обучения:
for ep in range(epochs):
for batch_x, batch_y in dataset: model.train_on_batch(batch_x, batch_y)
В некоторых случаях, например, при обучении с подкреплением [4] нельзя обойтись без явного вычисления градиентов и их последующего употребления для обновления весов НС:
for ep in range(epochs):
for batch_x, batch_y in dataset:
with tf.GradientTape() as tape:
y = h(batch_x)
y = h2(y)
y_pred = out(y)
loss = tf.losses.mean_squared_error(batch_y, y_pred)
# Обратное распространение
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
Во всех случаях после завершения обучения потери и точность классификации примеров проверочного множества можно вычислить следующим образом:
y_pred = model.predict(x_tst)
y_pred = np.array([np.argmax(x) for x in y_pred], dtype = 'float32')
loss = keras.losses.mean_squared_error(y_tst0, y_pred).numpy()
true_classified = np.sum(y_pred == y_tst0)
acc = round(true_classified / len(y_tst), 4)
print('loss =', round(loss, 4), 'acc =', acc)
Можно, как и ранее, применить evaluate:
scores = model.evaluate(x_tst, y_tst, verbose = 0)
loss = round(scores[0], 4)
acc = round(scores[1], 4)
print('loss =', loss, 'acc =', acc)
Полный код с рассмотренными в разделе вариантами обучения НС:
# kaggle.com/uciml/pima-indians-diabetes-database/data
# https://www.tensorflow.org/guide/autodiff
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
np.random.seed(22)
tf.random.set_seed(22)
how = 2
show_model = False
num_classes = 2
batch_size = 32 # Число примеров в пакете
epochs = 20
data = np.loadtxt('diab.csv', delimiter = ',') # 768 примеров
x = data[:, 0:8]
y = data[:, 8]
scaler = StandardScaler(copy = False).fit(x)
x = scaler.transform(x)
# Получаем обучающее и проверочнное множества
x_trn, x_tst, y_trn, y_tst = train_test_split(x, y, test_size = 0.2, random_state = 22)
if num_classes == 2:
y_tst0 = y_tst.copy() # Для оценки результатов обучения
y_trn = keras.utils.to_categorical(y_trn, num_classes)
y_tst = keras.utils.to_categorical(y_tst, num_classes)
last_activation = 'softmax'
else:
last_activation = 'sigmoid'
# Задаем несвязанные слои для употребления с GradientTape
inp = layers.Input(shape = (len(x_trn[0]), ))
h = layers.Dense(32, activation = 'relu')
h2 = layers.Dense(16, activation = 'relu')
out = layers.Dense(num_classes, activation = last_activation)
# Создание модели НС
y = h(inp)
y = h2(y)
model = keras.Model(inputs = inp, outputs = out(y))
if show_model: model.summary()
optimizer = keras.optimizers.Adam(learning_rate = 0.01)
# Компиляция модели
model.compile(loss = 'mse', optimizer = optimizer, metrics = ['accuracy'])
if how > 0:
dataset = tf.data.Dataset.from_tensor_slices((x_trn, y_trn))
dataset = dataset.batch(batch_size)
if how == 0:
model.fit(x_trn, y_trn, epochs = epochs, batch_size = batch_size, verbose = 0)
elif how == 1: # train_on_batch
for ep in range(epochs):
for batch_x, batch_y in dataset:
model.train_on_batch(batch_x, batch_y)
elif how == 2: # GradientTape
for ep in range(epochs):
for batch_x, batch_y in dataset:
with tf.GradientTape() as tape:
y = h(batch_x)
y = h2(y)
y_pred = out(y)
loss = tf.losses.mean_squared_error(batch_y, y_pred)
# Обратное распространение
grads = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
# Потери и точность
# Вариант 1
y_pred = model.predict(x_tst)
y_pred = np.array([np.argmax(x) for x in y_pred], dtype = 'float32')
loss = keras.losses.mean_squared_error(y_tst0, y_pred).numpy()
true_classified = np.sum(y_pred == y_tst0)
acc = round(true_classified / len(y_tst), 4)
print('loss =', round(loss, 4), 'acc =', acc)
# Вариант 2
scores = model.evaluate(x_tst, y_tst, verbose = 0)
loss = round(scores[0], 4)
acc = round(scores[1], 4)
print('loss =', loss, 'acc =', acc)
Рассмотрен пример употребления полносвязной нейронной сети (НС). Использована оболочка Keras, обеспечивающая доступ к TensorFlow. Приведен пример обучения НС на предварительно сформированных пакетах, а также пример явного вычисления градиентов и их последующего применения для оптимизации модели. Невысокая точность классификации объясняется непродолжительным обучением, малым размером обучающих данных и недостаточно продуманной архитектурой НС.