Список работ

Бартеньев О. В.

Параметры, влияющие на эффективность нейронной сети, созданной средствами Keras

Содержание

• Введение
• Параметры слоев нейронной сети
  • Задание слоев
  • Описание параметров слоев
  • Функции активации
  • Функции регуляризации
  • Функции ограничения
  • Инициализаторы
• Параметры, задаваемые при компиляция модели нейронной сети
  • Компиляция модели нейронной сети
  • Оптимизаторы
  • Функции потерь
• Параметры обучения нейронной сети
• Примеры структур моделей нейронных сетей
• Заключение
• Источники
• Приложение 1. Использование метрик
• Приложение 2. Обеспечение повторяемости результата
• Приложение 3. Пакетная нормализация

Введение

Создание нейронной сети (НС) средствами библиотеки Keras выполняется в следующем порядке:

1. Задаются слои НС и порядок их следования.
2. Выполняется компиляция НС.
3. Выполняется обучение НС.

Эффективность созданной НС можно и оценить на этапе тестирования по точности решения поставленной задачи, например, по точности классификации графических изображений:

acc = n_true / n,

где n – общее число классифицируемых на этапе тестирования изображений;
n_true – число правильно классифицированных на этапе тестирования изображений.
Более полно качество обучения НС можно оценить по показателям (вычисляются в разрезе классов):

• точность (precision);
• полнота (recall);
• F₁,

оперируя следующими значениями:

• true_positive - НС "сказала" "да", и это верно;
• false_positive - НС "сказала" "да", и это ошибка;
• true_negative - НС "сказала" "нет", и это верно;
• false_negative - НС "сказала" "нет", и это ошибка.

precision = true_positive / (true_positive + false_positive)
recall = true_positive / (true_positive + false_negative)
F₁ = 2 * precision * recall / (precision + recall)

Пример:

import numpy as np
from sklearn.metrics import classification_report
y_pred = np.array([0, 1, 2, 3, 0, 0, 2, 1, 1, 1, 2, 2, 2, 2, 2, 2]) # Прогноз
y_true = np.array([0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3]) # На самом деле
print(classification_report(y_true, y_pred, digits = 4))
tp, fp, tn, fn = [], [], [], []
for cls in range(4):
tp.append(np.sum(y_pred == cls, where = y_true == cls))
fp.append(np.sum(y_pred == cls, where = y_true != cls))
tn.append(np.sum(y_true == cls, where = y_pred == cls))
fn.append(np.sum(y_true == cls, where = y_pred != cls))
for cls in range(4):
precision = round(tp[cls] / (tp[cls] + fp[cls]), 4)
recall = round(tp[cls] / (tp[cls] + fn[cls]), 4)
F1 = 2 * precision * recall / (precision + recall)
print(precision, recall, round(F1, 4))

Результат:

На каждом этапе создания НС библиотека Keras предоставляет большой выбор параметров, влияющих на результативность НС. Поэтому перед пользователем, создающим НС, опираясь на методы библиотеки Keras, стоит непростая задача выбора правильных значений параметров. (В [1] отмечается, что невозможно дать обобщенные рекомендации по выбору параметров модели НС ввиду большого разнообразия НС и решаемых с их помощью задач.)
Ниже описываются методы, используемые при построении сверточных нейронных сетей с помощью следующих слоев:

• BatchNormalization – слой, обеспечивающий пакетную (batch) нормализацию (описана в [2]);
• Conv2D – сверточный 2D-слой;
• Dense – полносвязный слой;
• Dropout – слой, обнуляющий в модели НС часть весов;
• Flatten – слой, преобразующий 2D-данные в 1D-данные;
• Input – входной слой;
• MaxPooling2D – слой подвыборки, снижающий размерность поступивших на него данных.

Замечание. Многослойный перцептрон может быть создан как комбинация слоев Input, BatchNormalization, Dropout и Dense).

Слои Flatten и Input далее не рассматриваются, поскольку слой Flatten используется без параметров, а Input имеет неизменяемый параметр, задающий форму входных данных. Например, в задаче классификации изображений рукописных цифр:

inp = Input(shape = (28, 28, 1))

Форма (28, 28, 1) означает, что каждая цифра задана в виде рисунка размера 28*28 пикселей, выполненного в оттенках серого цвета.

Параметры слоев нейронной сети

Задание слоев

Задание слоев НС выполняется следующими методами [3, 4, 5]:

1. keras.layers.BatchNormalization(axis=-1, momentum=0.99, epsilon=0.001, center=True, scale=True, beta_initializer='zeros', gamma_initializer='ones', moving_mean_initializer='zeros', moving_variance_initializer='ones', beta_regularizer=None, gamma_regularizer=None, beta_constraint=None, gamma_constraint=None)
   Входная форма может быть произвольной. Необходимо использовать параметр input_shape (кортеж целых чисел), когда слой является первым в модели сети.
   Выходная форма повторяет входную форму.
2. keras.layers.Conv2D(filters, kernel_size, strides=(1, 1), padding='valid', data_format=None, dilation_rate=(1, 1), activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None)
3. keras.layers.Dense(units, activation=None, use_bias=True, kernel_initializer='glorot_uniform', bias_initializer='zeros', kernel_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, bias_constraint=None)
4. keras.layers.Dropout(rate, noise_shape=None, seed=None)
5. keras.layers.MaxPooling2D(pool_size=(2, 2), strides=None, padding='valid', data_format=None)

Описание параметров слоев

Параметры слоев описаны в табл. 1.
Таблица 1. Параметры слоев (перечислены в алфавитном порядке)

Функции активации

Функции активации [6], которые можно указать в качестве значения параметра activation при задании слоя (также эти функции можно задать и в виде слоя):

1. softmax(x, axis = -1) (здесь и далее x - входной тензор);
2. elu(x, alpha = 1.0) (Exponential linear unit), x, если x > 0 и alpha * (exp(x) - 1), если x < 0;
3. selu(x) (Scaled Exponential Linear Unit), scale * elu(x, alpha) ;
4. softplus(x), log(exp(x) + 1);
5. softsign(x), x / (abs(x) + 1);
6. relu(x, alpha = 0.0, max_value = None, threshold = 0.0) (Rectified Linear Unit), f(x) = max_value, если x >= max_value, f(x) = x, если threshold <= x < max_value и f(x) = alpha * (x - threshold) - в противном случае;
7. tanh(x) - гиперболический тангенс;
8. sigmoid(x);
9. hard_sigmoid(x) (вычисляется быстрее, чем sigmoid), возвращает 0, если x < -2.5, 1, если x > 2.5 и 0.2 * x + 0.5, если -2.5 <= x <= 2.5;
10. exponential(x) - e^x;
11. linear(x) - линейная функция активации (ничего не меняет).

Способы задания функций активации:

from keras.layers import Activation, Dense
model.add(Dense(64))
model.add(Activation('tanh'))

или

model.add(Dense(64, activation = 'tanh'))

или

from keras import backend as K
model.add(Dense(64, activation = K.tanh))

Функции активации, которые задаются в виде слоя [7]:

1. LeakyReLU(alpha = 0.3) (Leaky version of a Rectified Linear Unit), f(x) = alpha * x, если x < 0 и f(x) = x, если x >= 0;
2. PReLU(alpha_initializer = 'zeros', alpha_regularizer = None, alpha_constraint = None, shared_axes = None) (Parametric Rectified Linear Unit), f(x) = alpha * x, если x < 0 и f(x) = x, если x >= 0, где alpha - обучаемый массив той же формы, что и x (x - вход PReLU-слоя);
3. ELU(alpha = 1.0) (Exponential Linear Unit), f(x) = alpha * (exp(x) - 1.), если x < 0, f(x) = x, если x >= 0;
4. ThresholdedReLU(theta = 1.0) (Thresholded Rectified Linear Unit), f(x) = x, если x > theta, f(x) = 0 - в противном случае (theta >= 0, тип theta - float);
5. Softmax(axis = -1);
6. ReLU(max_value = None, negative_slope = 0.0, threshold = 0.0) (Rectified Linear Unit), f(x) = max_value, если x >= max_value, f(x) = x, если threshold <= x < max_value и f(x) = negative_slope * (x - threshold) - в противном случае.

Возможный способ задания функции активации (на примере LeakyReLU):

from keras.layers import LeakyReLU
hidden2_3 = Dense(12)(hidden2_2)
hidden2_4 = LeakyReLU(alpha = 0.4) (hidden2_3)

Функции регуляризации

Функции регуляризации позволяют применять штрафы к параметрам слоя или активности слоя во время обучения сети. Эти штрафы включены в функцию потерь, которую оптимизирует сеть.
Доступны следующие штрафы [8] (в скобках указаны заданные по умолчанию значения коэффициентов регуляризации):

1. keras.regularizers.l1(0.)
2. keras.regularizers.l2(0.)
3. keras.regularizers.l1_l2(l1=0.01, l2=0.01)
4. Функция регуляризации, заданная пользователем.

Функции ограничения

Эти функции позволяют устанавливать ограничения на значения параметров сети во время оптимизации.
Доступны следующие функции ограничения [9]:

1. keras.constraints.MaxNorm(max_value=2, axis=0) – вес каждого нейрона скрытого слоя будет иметь норму, небольшую заданного значения max_value. Здесь далее axis – измерение, по которому применяется ограничение.
2. keras.constraints.NonNeg() – веса НС будут неотрицательны.
3. keras.constraints.UnitNorm(axis=0) – вес каждого нейрона скрытого слоя будет иметь единичную норму.
4. keras.constraints.MinMaxNorm(min_value=0.0, max_value=1.0, rate=1.0, axis=0) – вес каждого нейрона скрытого слоя будет иметь норму между нижней (min_value) и верхней (max_value) границами. rate – скорость соблюдения ограничений. rate = 1.0 означает строгое соблюдение ограничения; rate < 1.0 означает, что веса будут масштабироваться на каждом шаге обучения, приближаясь к значению между min_value и max_value.

Инициализаторы

Инициализатор определяет способ задания начальных случайных весов слоев Keras. Доступны следующие инициализаторы [10]:

1. keras.initializers.Initializer() – базовый класс. Все инициализаторы наследуют из этого класса.
2. keras.initializers.Zeros() – тензоры инициализируются числом 0.
3. keras.initializers.Ones() – тензоры инициализируются числом 1.
4. keras.initializers.Constant(value=0) – тензоры инициализируются заданным значением value.
5. keras.initializers.RandomNormal(mean=0.0, stddev=0.05, seed=None) – тензоры инициализируются с использованием нормального распределения.
6. keras.initializers.RandomUniform(minval=-0.05, maxval=0.05, seed=None) – тензоры инициализируются с использование равномерного распределения значениями из диапазона [minval, maxval].
7. keras.initializers.TruncatedNormal(mean=0.0, stddev=0.05, seed=None) – тензоры инициализируются с использованием усеченного нормального распределения.
8. keras.initializers.VarianceScaling(scale=1.0, mode='fan_in', distribution='normal', seed=None) – при distribution="normal" начальные значения весов берутся из усеченного нормального распределения с центром в нуле и stddev = sqrt(scale / n), где n – число входных, выходных и среднее входных и выходных единиц соответственно при mode='fan_in', mode='fan_out' и mode='fan_avg'; при distribution="uniform" начальные значения весов берутся из равномерного распределения в пределах [-limit, limit], где limit = sqrt(3 * scale / n).
9. keras.initializers.Orthogonal(gain=1.0, seed=None) – генерирует случайную ортогональную матрицу.
10. keras.initializers.Identity(gain=1.0) – генерирует единичную матрицу.
11. keras.initializers.lecun_uniform(seed=None) – генерирует веса из равномерного распределения в пределах [-limit, limit], где limit = sqrt(3 / fan_in).
12. keras.initializers.glorot_normal(seed=None) – генерирует веса из усеченного нормального распределения с центром 0 и stddev = sqrt(2 / (fan_in + fan_out)).
13. keras.initializers.glorot_uniform(seed=None) – генерирует веса из равномерного распределения в пределах [-limit, limit], где limit = sqrt(6 / (fan_in + fan_out)).
14. keras.initializers.he_normal(seed=None) – генерирует веса из усеченного нормального распределения с центром 0 и stddev = sqrt(2 / fan_in).
15. keras.initializers.lecun_normal(seed=None) – генерирует веса из усеченного нормального распределения с центром 0 и stddev = sqrt(1 / fan_in).
16. keras.initializers.he_uniform(seed=None) – генерирует веса из равномерного распределения в пределах [-limit, limit], где limit = sqrt(6 / fan_in).
17. Инициализатор, заданный пользователем.

Параметры инициализаторов приведены в табл. 2.
Таблица 2. Параметры инициализаторов (перечислены в алфавитном порядке)

Параметры, задаваемые при компиляция модели нейронной сети

Компиляция модели нейронной сети

Компиляция модели НС выполняется в результате употребления метода compile [11]:

compile(optimizer, loss=None, metrics=None, loss_weights=None, sample_weight_mode=None, weighted_metrics=None, target_tensors=None)

Параметры метода приведены в табл. 3.
Таблица 3. Параметры метода compile

Оптимизаторы

Доступны следующие оптимизаторы [12]:

1. keras.optimizers.SGD(lr=0.01, momentum=0.0, decay=0.0, nesterov=False, clipnorm=1.0, clipvalue=0.5) – стохастический градиентный спуск.
2. keras.optimizers.RMSprop(lr=0.001, rho=0.9, epsilon=None, decay=0.0, clipnorm=1., clipvalue=0.5) – делит скорость обучения для веса на скользящее среднее значение последних градиентов этого веса.
3. keras.optimizers.Adagrad(lr=0.01, epsilon=None, decay=0.0, clipnorm=1., clipvalue=0.5) – скорость обучения параметра (веса) зависит от частоты его обновления: чем чаще обновляется параметр, тем меньше скорость его обучения.
4. keras.optimizers.Adadelta(lr=1.0, rho=0.95, epsilon=None, decay=0.0, clipnorm=1., clipvalue=0.5) – расширение Adagrad, в котором скорости обучения изменяются на основе движущегося окна обновлений градиентов, а не на основе значений всех прежних градиенты, как в Adagrad. Таким образом, Adadelta продолжает учиться, даже если было сделано много обновлений. В оригинальной версии Adadelta не нужно устанавливать начальную скорость обучения. В версии Keras начальную скорость обучения можно задать, отличной от 0.01.
5. keras.optimizers.Adam(lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, amsgrad=False, clipnorm=1., clipvalue=0.5) – вариант стохастической оптимизации.
6. keras.optimizers.Adamax(lr=0.002, beta_1=0.9, beta_2=0.999, epsilon=None, decay=0.0, clipnorm=1., clipvalue=0.5) – вариант алгоритма Adam, основанный на бесконечной норме.
7. keras.optimizers.Nadam(lr=0.002, beta_1=0.9, beta_2=0.999, epsilon=None, schedule_decay=0.004, clipnorm=1., clipvalue=0.5) – алгоритм Адама, использующий импульс Нестерова [13].

Параметры оптимизаторов приведены в табл. 4.
Таблица 4. Параметры оптимизаторов (перечислены в алфавитном порядке)

Функции потерь

Доступные следующие функции потерь [15]:

1. keras.losses.mean_squared_error(y_true, y_pred)
2. keras.losses.mean_absolute_error(y_true, y_pred)
3. keras.losses.mean_absolute_percentage_error(y_true, y_pred)
4. keras.losses.mean_squared_logarithmic_error(y_true, y_pred)
5. keras.losses.squared_hinge(y_true, y_pred)
6. keras.losses.hinge(y_true, y_pred)
7. keras.losses.categorical_hinge(y_true, y_pred)
8. keras.losses.logcosh(y_true, y_pred)
9. keras.losses.categorical_crossentropy(y_true, y_pred)
10. keras.losses.sparse_categorical_crossentropy(y_true, y_pred)
11. keras.losses.binary_crossentropy(y_true, y_pred)
12. keras.losses.kullback_leibler_divergence(y_true, y_pred)
13. keras.losses.poisson(y_true, y_pred)
14. keras.losses.cosine_proximity(y_true, y_pred)
15. Функция потерь, заданная пользователем.

y_true, y_pred – тензоры, содержащие соответственно истинные и предсказанные значения меток.
Подробное описание функций потерь, имеющихся в библиотеке Keras, дано в [16].

Параметры обучения нейронной сети

Обучение НС выполняется в результате обращения к методу fit [11]:

fit(x=None, y=None, batch_size=None, epochs=1, verbose=1, callbacks=None, validation_split=0.0, validation_data=None, shuffle=True, class_weight=None, sample_weight=None, initial_epoch=0, steps_per_epoch=None, validation_steps=None)

Параметры метода fit приведены в табл. 5.
Таблица 5. Параметры метода fit

Метод fit возвращает объект типа History. Его свойство History.history содержит значения потерь и заданных метрик после завершения каждой эпохи обучения, а также значения потерь и метрик последующего тестирования (если оно предусмотрено по завершению эпохи).

Примеры структур моделей нейронных сетей

Показаны на рис. 1 – 3.

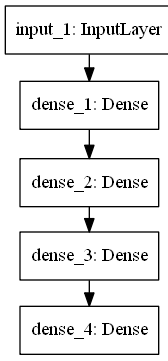
Рис. 1. Пример структуры многослойного перцептрона

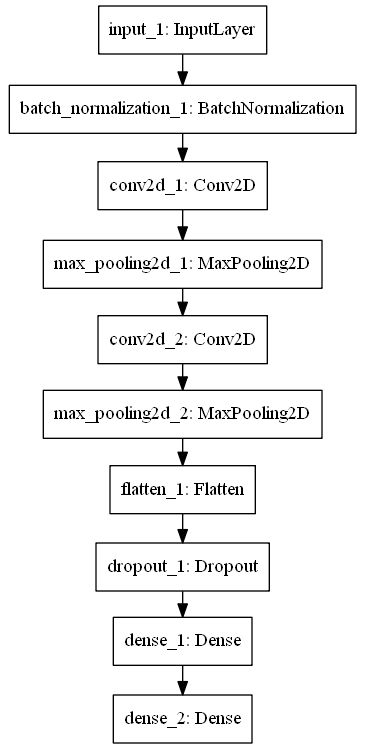
Рис. 2. Пример структуры сверточной нейронной сети

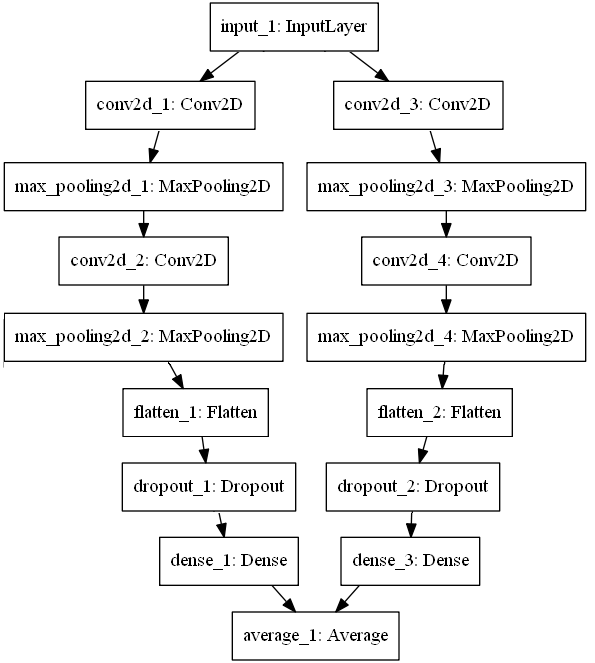
Рис. 3. Пример структуры сборки сверточных нейронных сетей с двумя ветвями

Для объединения идущих по ветвям сборки данных используется слой Average. Иные способы объединения данных описаны в [17]; вот их список:

• Add() – суммирует поступающие на вход слоя тензоры; форма всех тензоров одинакова;
• Multiply() – возвращает тензор, содержащий произведение входных тензоров; форма всех тензоров одинакова;
• Average() – возвращает тензор, содержащий средние значения входных тензоров; форма всех тензоров одинакова;
• Maximum() – возвращает тензор, содержащий максимальные значения входных тензоров (максимумы ищутся поэлементно); форма всех тензоров одинакова;
• Minimum() – возвращает тензор, содержащий минимальные значения входных тензоров (минимумы ищутся поэлементно); форма всех тензоров одинакова;
• Concatenate(axis=-1) – возвращает тензор, вычисляемый как объединение входных тензоров, имеющих одинаковую форму за исключением оси axis, по которой выполняется объединение;
• Dot(axes, normalize=False) – возвращает скалярное произведение входных тензоров:пусть на входе 2 тензора a и b формы (batch_size, n), тогда на выходе будет тензор формы (batch_size, 1), каждый i-й элемент которого – это скалярное произведение a[i] и b[i].

Заключение

Известны советы относительно применения некоторых рассмотренных выше параметров:

1. Оптимизатор RMSProp рекомендуется применять в рекуррентных НС [12].
2. Не рекомендуется изменять заданные по умолчанию значения параметров оптимизаторов Adagrad, Adadelta и Nadam [12].
3. Эффективность обучении больших НС избыточными обучающими данными будет выше, если употреблять достаточно большие пакеты обучения (параметр batch_size) [1].
4. Следует инициализировать веса скрытых слоев различными значениями и задавать разные смещения. В противном случае градиенты этих слоев будут одинаковы, а сами слои функционально неразличимы [1].
5. При обучении большими избыточными наборами данных следует отдавать предпочтение методам оптимизации с накоплением импульса [1].
6. Правильно выбирать начальное значение скорости обучения [1, 18].
7. Полезно иметь программу, которая автоматически [1, 18]:
   • уменьшит скорость обучения, если потери растут или осциллируют в широком диапазоне;
   • увеличит скорость обучения, если потери постоянно уменьшаются, но очень медленно.

В частности, в [19] используются следующие средства управления скоростью обучения:

import keras.callbacks as cb
#
# Параметр функции обратного вызова LearningRateScheduler
# Изменяет скорость обучения в зависимости от числа пройденных эпох
def lr_schedule(epoch):
    lr = 1e-3
    if epoch>180:
        lr *= 0.5e-3
    elif epoch>160:
        lr *= 1e-3
    elif epoch>120:
        lr *= 1e-2
    elif epoch>80:
        lr *= 1e-1
    print('Скорость обучения:', lr)
    return lr
#
# Функция обратного вызова, задающая график изменения скорости обучения
lr_scheduler = cb.LearningRateScheduler(lr_schedule)
# Функция обратного вызова, снижающая скорость обучения, если потери val_loss не снижаются patience эпох
lr_reducer = cb.ReduceLROnPlateau(factor = np.sqrt(0.1), cooldown = 0, patience = 5, min_lr = 0.5e-6)
# Список функций обратного вызова
callbacks_list = [lr_reducer, lr_scheduler]
# Обучение модели
history = model.fit(<другие параметры метода fit>, callbacks = callbacks_list)

Приложение 1. Использование метрик

Метрика – это функция, используемая для оценки эффективности модели НС [20]. Метрики задаются параметром metrics (в виде списка) метода compile, например:

model.compile(loss = 'mean_squared_error', optimizer = 'sgd', metrics = ['mae', 'acc'])

или

from keras import metrics
model.compile(loss = 'mean_squared_error', optimizer = 'sgd', metrics = [metrics.mae, metrics.categorical_accuracy])

Функция метрики схожа с функцией потерь, однако результат оценки сети по метрике не используется при обучении модели. В качестве метрики может быть использована любая функция потерь.
Также в качестве метрики можно указать имя доступной метрики, например, 'accuracy' символьную функцию Theano/TensorFlow.

Параметры функции метрики:

• y_true – истинные метки; тип данных: тензор Theano/TensorFlow.
• y_pred – прогноз НС; тип данных: тензор Theano/TensorFlow той же формы, что и y_true.

Функция метрики возвращает единичный тензор, представляющий среднее значение по всем элементам массива, вычисляемого по входным данным в соответствии с заданной метрикой.

Доступные метрики:

• binary_accuracy; пример: keras.metrics.binary_accuracy(y_true, y_pred);
• categorical_accuracy; keras.metrics.categorical_accuracy(y_true, y_pred);
• sparse_categorical_accuracy; keras.metrics.sparse_categorical_accuracy(y_true, y_pred);
• top_k_categorical_accuracy; keras.metrics.top_k_categorical_accuracy(y_true, y_pred, k = 5);
• sparse_top_k_categorical_accuracy; keras.metrics.sparse_top_k_categorical_accuracy(y_true, y_pred, k = 5).
• любая встроенная функция потерь [15].

Пользовательские функции метрики так же должны иметь два параметра (y_true, y_pred) и возвращать единичный тензор, например:

import keras.backend as K
def mean_pred(y_true, y_pred):
    return K.mean(y_pred)
model.compile(optimizer = 'rmsprop', loss='binary_crossentropy', metrics=['accuracy', mean_pred])

Замечание 2. Для функции потерь binary crossentropy в случае указания метрики 'accuracy' возвращает завышенные значения точности (binary_accuracy).
Чтобы получить реальную точность, с binary crossentropy используется вдобавок метрика categorical_accuracy:

metrics = ['accuracy', keras.metrics.categorical_accuracy]

Приложение 2. Обеспечение повторяемости результата

Воспроизведение результатов эпизода обучения обеспечивает следующий код [20], который должен быть исполнен до начала создания НС и ее обучения:

# Флаг задания режима воспроизведения результатов
repeat_results = True # True
seedVal = 348
import numpy as np
np.random.seed(seedVal) # Задание затравки датчика случайных чисел
#
if repeat_results:
    print('Режим воспроизведения (повторяемости) результатов')
    import random as rn
    import tensorflow as tf
    import os
    from keras import backend as K
    # Код, необходимый для воспроизведения результата
    os.environ['PYTHONHASHSEED'] = '0'
    rn.seed(seedVal)
    tf.set_random_seed(seedVal)
    session_conf = tf.ConfigProto(intra_op_parallelism_threads = 1,
                                 inter_op_parallelism_threads = 1)
    sess = tf.Session(graph = tf.get_default_graph(), config = session_conf)
    K.set_session(sess)

В этом коде фиксируются затравки датчиков случайных чисел, значение системной переменной PYTHONHASHSEED и устанавливается в сессии tensorFlow однопоточность.

Неповторяемость результата обучения возникает также при использовании TensorFlow на GPU: некоторые операции, в частности tf.reduce_sum(), имеют нечеткий результат. Это обусловлено тем, что на GPU многие операции исполняются параллельно, поэтому порядок выполнения не всегда гарантирован. Из-за ограниченной точности вычислений даже сложение нескольких чисел может дать разные результаты при разных порядках выполнения этой операции. Можно попытаться при программировании избежать нечетких операций, но некоторые могут быть созданы автоматически TensorFlow при вычислении градиентов. Проще всего добиться повторяемости результатов, выполняя код на CPU. Для этого следует переменную окружения CUDA_VISIBLE_DEVICES инициализировать пустой строкой, например [21]:

$ CUDA_VISIBLE_DEVICES="" PYTHONHASHSEED=0 python your_program.py

Приложение 3. Пакетная нормализация

Градиентные методы, лежащие в основе алгоритмов машинного обучения, весьма чувствительны к распределению индивидуальных признаков: результативность алгоритмов может быть неудовлетворительной, если распределение индивидуального признака существенно отличается от стандартного нормального распределения, имеющего нулевое математическое ожидание и единичную дисперсию.
Изменение распределения признака выполняется в результате нормализации или стандартизации.
Нормализация предполагает такое масштабирование признака, после которого он имеет единичную норму (l1 или l2).
Стандартизация – такое преобразование данных, после которого среднее значение каждого признака равно 0, а дисперсия равна 1 (то есть, как в стандартном нормальном распределении).
В библиотеке Scikit-Learn есть следующие функции нормализации и стандартизации:

from sklearn import preprocessing
normalized_X = preprocessing.normalize(X, norm = 'l2') # Нормализация (другая норма – 'l1')
standardized_X = preprocessing.scale(X) # Стандартизация
# Иная возможность нормализации и стандартизации данных
normalizer = preprocessing.Normalizer().fit(X)
X = normalizer.transform(X)
# fit – вычисляет среднее значение и стандартное отклонение для последующей стандартизации
scaler = preprocessing.StandardScaler(copy = False).fit(X)
X = scaler.transform(X) # Стандартизация за счет центрирования и масштабирования

В случае НС на вход 1D-слоя подается тензор формы (размер_пакета, карта_признаков), то есть пакет признаков. Поэтому нормализация признаков НС называется пакетной. Пакетная нормализация выполняется по следующему алгоритму [2]:

Входные данные: значения x из пакета B = {x₁, x₂, ..., x_m} (x_i – индивидуальный признак; m – размер пакета); обучаемые параметры γ и β; константа ε для вычислительной устойчивости.

Выходные данные: {y_i = BN_{γ, β}(x_i)}

Пакетная нормализация позволяет:

• уменьшить расхождение математических ожиданий и дисперсий признаков пакета;
• ускорить поиск решения, несмотря на выполнение дополнительных вычислений;
• каждому слою сети обучатся более независимо от других слоев;
• использовать более высокую скорость обучения (на выходах слоя НС нет чрезмерно больших или малых значений);
• осуществлять, в известной мере, регуляризацию, поскольку привносит в выходы слоя НС некоторый шум;
• сделать НС менее чувствительной к начальной инициализации весов.

Согласно [2], выполняемая по приведенному выше алгоритму пакетная нормализация, уменьшает эффект внутреннего сдвига переменных (internal covariate shift). Этот эффект иллюстрирует рис. П1 (пример взят из [22]).

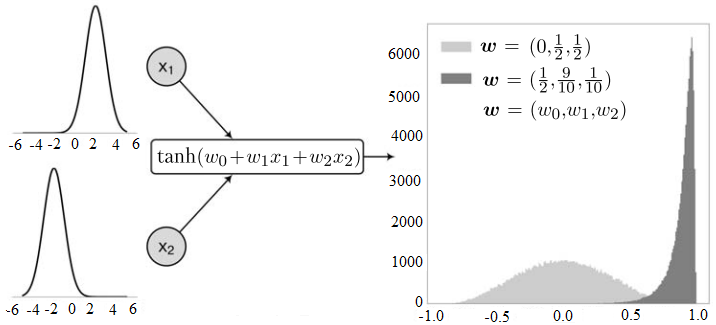
Рис. П1. Иллюстрация эффекта внутреннего сдвига

На рис. П1 представлен нейрон первого слоя с двумя входами и функцией активации tanh.
Предполагается, что на входы нейрона подаются нормально распределенные данные со средними значениями 2 и -2 и дисперсией 0.5. Эти распределения показаны в левой части рис. П1.
В правой части рис. П1 показаны распределения выхода нейрона для случаев w = (0, 0.5, 0.5) и w = (0.5, 0.9, 0.1). Эти распределения построены в результате выполнения программы, генерирующей входные данные (согласно заданным распределениям на входе) и вычисляющий выход

y = tanh(w₀ + w₁x₁ + w₂x₂).

Нейрон второго слоя первоначально обучится реагировать на входы из распределения, получаемого при весах w = (0, 0.5, 0.5) нейрона первого слоя, то есть на данные преимущественно из интервала [-0.5, 0.5]. Однако после изменения весов нейрона первого слоя выход этого нейрона попадает в интервал [0.5, 1] (чаще ближе к 1), то есть нейрон второго слоя придется обучать заново.
Пакетная нормализация позволяет устранить эту проблему, получившую название внутреннего сдвига переменных.

Источники

1. Hinton G., Srivastava N., Swersky K. Neural networks for machine learning. [Электронный ресурс] URL: http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf (дата обращения: 01.01.2019).
2. Sergey Ioffe, Christian Szegedy. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. [Электронный ресурс] URL: https://arxiv.org/abs/1502.03167 (дата обращения: 01.01.2019).
3. Normalization Layers. BatchNormalization. [Электронный ресурс] URL: https://keras.io/layers/normalization/ (дата обращения: 01.01.2019).
4. Convolutional layers. [Электронный ресурс] URL: https://keras.io/layers/convolutional/ (дата обращения: 01.01.2019).
5. Core layers. [Электронный ресурс] URL: https://keras.io/layers/core/ (дата обращения: 01.01.2019).
6. Keras activations. [Электронный ресурс] URL: https://keras.io/activations/ (дата обращения: 01.01.2019).
7. Keras advanced activations. [Электронный ресурс] URL: https://keras.io/layers/advanced-activations/ (дата обращения: 01.01.2019).
8. Keras regularizers. [Электронный ресурс] URL: https://keras.io/regularizers/ (дата обращения: 01.01.2019).
9. Keras constraints. [Электронный ресурс] URL: https://keras.io/constraints/ (дата обращения: 01.01.2019).
10. Keras initializers. [Электронный ресурс] URL: https://keras.io/initializers/ (дата обращения: 01.01.2019).
11. Model class API. [Электронный ресурс] URL: https://keras.io/models/model/https://keras.io/initializers/ (дата обращения: 01.01.2019).
12. Keras optimizers. [Электронный ресурс] URL: https://keras.io/optimizers/ (дата обращения: 01.01.2019).
13. Incorporating Nesterov Momentum into Adam URL: http://cs229.stanford.edu/proj2015/054_report.pdf (дата обращения: 01.01.2019).
14. On the Convergence of Adam and Beyond. [Электронный ресурс] URL: https://openreview.net/forum?id=ryQu7f-RZ (дата обращения: 01.01.2019).
15. Keras losses. [Электронный ресурс] URL: https://keras.io/losses/ (дата обращения: 01.01.2019).
16. Функции потерь библиотеки Keras. [Электронный ресурс] URL: http://100byte.ru/python/loss/loss.html (дата обращения: 01.01.2019).
17. Merge Layers. [Электронный ресурс] URL: https://keras.io/layers/merge/ (дата обращения: 01.01.2019).
18. Zulkifli H. Understanding Learning Rates and How It Improves Performance in Deep Learning. [Электронный ресурс] URL: https://towardsdatascience.com/understanding-learning-rates-and-how-it-improves-performance-in-deep-learning-d0d4059c1c10 (дата обращения: 01.01.2019).
19. Keras Documentation. CIFAR-10 ResNet. . [Электронный ресурс] URL: https://keras.io/examples/cifar10_resnet/ (дата обращения: 01.01.2019).
20. Usage of metrics. [Электронный ресурс] URL: https://keras.io/metrics/ (дата обращения: 01.01.2019).
21. Keras documentation. How can I obtain reproducible results using Keras during development? [Электронный ресурс] URL: https://keras.io/getting-started/faq/#how-can-i-obtain-reproducible-results-using-keras-during-development (дата обращения: 01.01.2019).
22. Николенко С., Кадурин А., Архангельская Е. Глубокое обучение. – СПб.: Питер, 2018. – 480 с.

Список работ