Рассматривается задача стабилизации шеста, расположенного на подвижной платформе [1] (рис. 1).
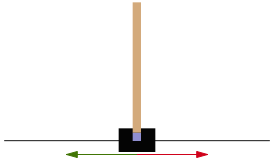
Рис. 1. Шест на тележке, или перевернутый маятник
Шест удерживается в вертикальном состоянии за счет изменения скорости тележки.
Управление шестом на тележке можно описать марковским процессом. В таких процессах управляющее действие определяется только текущим состоянием объекта управления и не зависит от предшествующих состояний.
Для таких процессов применим принцип оптимальности Беллмана.
Задача решается с использованием объекта CartPole-v1 библиотеки gym [2].
Для решения задачи необходимо в каждом состоянии s объекта управления правильно определять действие a, оказываемое на тележку с шестом.
Возможны два действия: толкнуть тележку влево и толкнуть вправо.
Задача стабилизации шеста на тележке решается с помощью агента, взаимодействующего с средой, фиксирующей в том числе и состояние объекта – тележки с шестом.
Среда передает агенту состояние объекта управления и награду за действие агента, переведшее объект в текущее состояние. Агент, получив от среды информацию о состоянии объекта и свою награду, определяет следующее действие, которое он считает наиболее правильным в сложившихся обстоятельствах. Сведения о своем решении он передает среде, которая и предпринимает соответствующее действие (рис. 2).
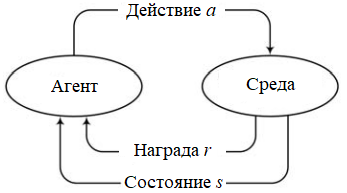
Рис. 2. Схема взаимодействия агента со средой
CartPole-v1 это модель среды, в которой можно управлять тележкой, по центру которой посредством шарнира прикреплен шест (маятник) (см. рис. 1).
Тележка перемещается по горизонтальному рельсу. Силы трения и сопротивления отсутствуют. Шест в момент начала симуляции (игры) находится (почти) в вертикальном положении.
Цель игры – предотвратить падение шеста. Это достигается за счет изменения скорости тележки. Скорость меняется в результате приложения к тележке горизонтальной силы, равной +1 или -1.
Среда задается состоянием, действием, наградой, начальным состоянием и флагом завершения эпизода.
Состояние описывается следующими величинами:
Действие может принимать два значения – 0 и 1:
Награда на каждом шаге равна 1, включая и последний шаг.
Начальное состояние задается при помощи датчика равномерно распределенных случайных чисел.
Случаи завершения эпизода:
Задача считается решенной, если средняя награда среды в течение 100 последовательных эпизодов не менее 195.
Замечание. Описание CartPole-v0, версии, предшествующей CartPole-v1, приведено в [3].
В рассматриваемой ниже программе используется метод Q-обучения агента. Метод реализует обучение с подкреплением на основе ценности.
Q-обучение - это алгоритм с разделенной стратегией: для обновления текущей стратегии используется опыт, накопленный при реализации разных стратегий (не только текущей, в отличие от SARSA).
В Q-обучении две стратегии: целевая (постоянно улучшается) и поведенческая ε-жадная, используемая для взаимодействия со средой.
При Q-обучении агент на основе сведений о состоянии s объекта управления и полученного от среды вознаграждения r, за действие a, переведшее объект в следующее состояние, вычисляет значение функции Q(s, a), оценивающей ценность действия a в состоянии s.
Функция Q вычисляется следующим образом:
Q(st, at) := Q(st, at) + α * (rt + 1 + γ * maxa Q(st + 1, a) – Q(st, at)), (*)
где α – скорость обучения функции ценности действия;
rt + 1 – награда, полученная от окружающей среды за действие a;
γ – коэффициент уменьшения вознаграждения (ценность терминального состояния, коэффициент обесценивания).
Соотношение (*) выражает принцип оптимальности Беллмана.
Полученное значение Q используется, во-первых, для обучения агента, а во-вторых, для определения следующего действия.
В приводимой ниже реализации значение Q определяется нейронной сетью (НС) – многослойным перцептроном (по аналогии с [4]).
Обучение агента состоит в подготовке данных для обучения НС и ее последующего обучения по этим данным.
НС имеет следующую структуру:
Layer (type) Output Shape Param #
=======================================
dense_0 (Dense) (None, 512) 2560
dense_1 (Dense) (None, 256) 131328
dense_2 (Dense) (None, 64) 16448
dense_3 (Dense) (None, 2) 130
=======================================
Total params: 150,466
Trainable params: 150,466
Non-trainable params: 0
На вход сети подается состояние объекта (state – массив формы(1, 4)). В качестве цели обучения определяются значения ценности действий 0 и 1 в состоянии state.
Для обучения агента формируется коллекция memory следующих значений:
Обучение агента выполняется по следующему алгоритму:
Выбрать случайным образом из memory коллекцию minibatch из batch_size значений.
Для каждого state, action, reward, state_next, done из minibatch Цикл
получить по state прогноз НС: q_values = self.model.predict(state);
определить текущую оценку ценности действия action: Qsa = q_values[0][action];
получить по state_next прогноз НС: q_values_next = self.model.predict(state_next);
вычислить по соотношению (*) новую оценку Qsa ценности действия action;
сформировать цель обучения НС: q_values[0][action] = Qsa;
провести обучение НС: self.model.fit(state, q_values, epochs = 1, verbose = 0).
КонецЦикла
Замечание. Форма входа НС – (?, 4); форма выхода НС – (?, 2).
Пример:
state = [[-0.006 0.411 -0.073 -0.772]];
q_values = self.model.predict(state) = [[0.053 0.528]];
state_next = [[ 0.002 0.217 -0.0889 -0.504]];
q_values_next = self.model.predict(state_next) = [[0.039 0.027]];
reward = 1.0;
action = 0;
γ = 0.95;
α = 1.0, поэтому
Qsa = 1.0 + 0.95 * max(0.039, 0.027) = 1.037;
q_values = [[1.037 0.0528]] (после корректировки – цель обучения);
q_values = [[0.076 0.047]] (после обучения НС; на входе [[-0.006 0.411 -0.073 -0.772]]).
Задача сети – предсказать по текущему состоянию значения ценности возможных действий: толкнуть тележку влево или вправо.
Сеть получает на входе состояние – массив state формы (1, 4), содержащий позицию тележки, ее скорость, угол отклонения шеста и скорость изменения этого угла.
Выход сети – это массив формы (1, 2):
q_values = self.model.predict(state)
Значение следующего действия, передаваемое окружению, – это индекс (0 или 1) массива q_values[0], отвечающий максимальному элементу массива, то есть действию с наибольшей ценностью:
action = np.argmax(q_values[0])
Создать среду: env = gym.make('CartPole-v1')
Создать агента: q_agent = Q_model(4, 2)
scores = {} // Хранит длительность игры в последних 100 эпизодах. Тип collections.deque
Неудача = Истина
Для Эпизод = 1 По 1000 Цикл // Предельное число эпизодов может быть иным
Получить начальное состояние объекта: state = env.reset()
ВремяИгры = 0
Пока Истина Цикл // Начинаем очередную игру
ВремяИгры = ВремяИгры + 1
Определить очередное действие: action = q_agent.findAction(state)
Получить от среды состояние объекта, награду и флаг завершения игры
после выполнения действия action: state_next, reward, done = env.step(action)
Запоминаем предыдущее состояние объекта, действие, награду, текущее состояние и done:
q_agent.remember(state, action, reward, state_next, done)
КонецЦикла
Запоминаем время игры: scores.append(ВремяИгры)
Если Эпизод > 100 Тогда
Вычислить score_mean – среднее время последних 100 игр
Если score_mean > 195 Тогда
Сообщить('Цель достигнута. Средняя продолжительность игры: ', score_mean)
Неудача = Ложь
Выйти из цикла
КонецЕсли
КонецЕсли
Выполнить обучение агента
КонецЦикла
Если Неудача = Истина Тогда
Сообщить('Задача не решена')
КонецЕсли
Выполнена на Python / Keras[5].
Агент обучается, взаимодействуя со средой. Взаимодействие обеспечивает коллекция history.
# https://programmersought.com/article/87216618118/
import gym
import numpy as np
from collections import deque
from keras.models import Model
from keras.layers import Input, Dense
from tensorflow.keras.optimizers import Adam
from sys import exit
import random
#
render = False
show_model = False
#
# Агент с Q-обучением
class Q_model():
#
def __init__(self, observation_space, action_space):
self.state_dim = observation_space
self.action_dim = action_space
self.history = deque(maxlen = 2000) # Тип collections.deque
self.alpha = 0.3 # Скорость обучения функции ценности действий
self.gamma = 0.95 # Коэффициент уменьшения вознаграждения агента
self.eps = 1.0 # Начальная вероятность случайного действия
self.epsilon_decay = 0.999 # Коэффициент уменьшения eps на каждом шаге обучения
self.epsilon_min = 0.005 # Минимальное значение eps
self.learning_rate = 0.001 # Скорость обучения НС
self.model = self.build_model() # Создаем модель НС
#
# Создает модель НС
def build_model(self):
inp = Input(self.state_dim)
x = Dense(256, activation = 'relu')(inp)
x = Dense(64, activation = 'relu')(x)
out = Dense(2, activation = 'linear')(x) # linear, sigmoid
model = Model(inp, out)
if show_model: model.summary()
optimizer = Adam(learning_rate = self.learning_rate)
model.compile(loss = 'mse', optimizer = optimizer)
return model
#
def find_action(self, state): # Случайный выбор действия a (0 или 1)
if np.random.rand() < self.eps: # Исследование
a = random.randrange(self.action_dim)
else: # Выбор действия согласно прогнозу НС
Q = self.model.predict(state) # [[72.89 63.46]]
a = np.argmax(Q) # Выбираем наиболее ценное действие
return a
#
def replay(self, batch_size):
if len(self.history) < batch_size: return # Случай короткой истории
# Обучение агента после каждого шага
# Случайная выборка (без повторов) batch_size элементов истории
minibatch = random.sample(self.history, batch_size)
states = np.array([d[0] for d in minibatch])
next_states = np.array([d[3] for d in minibatch])
Q = self.model.predict(states)
Q1 = self.model.predict(next_states)
# Формируем Q - цель обучения
for i, (_, a, reward, _, _) in enumerate(minibatch):
q = Q[i, a]
q1 = np.amax(Q1[i])
Q[i, a] = q + self.alpha * (reward + self.gamma * q1 - q)
self.model.train_on_batch(states, Q) # Обучение агента
if self.eps > self.epsilon_min: # Уменьшаем вероятность выбора случайного действия
self.eps *= self.epsilon_decay
# states[i] = [0.144 0.227 -0.209 -0.801]
# q[i]: [0.024 -0.008] - numpy.ndarray
# action = 1
# reward = 1.0
# target = 1.024
# y[i] = [0.001 1.0235]
#
if __name__ == "__main__":
env = gym.make('CartPole-v1') # Создаем среду. Тип: # <TimeLimit<CartPoleEnv<CartPole-v1>>>
observation_space = env.observation_space.shape[0] # 4
action_space = env.action_space.n # 2
# Q-нейронная сеть
q_agent = Q_model(observation_space, action_space) # Создаем агента
episodes = 300 # Число игровых эпизодов
batch_size = 32
for ep in range(episodes):
# Получаем начальное состояние объекта перед началом каждой игры (каждого эпизода)
state = env.reset() # Как вариант: state = [0.036 -0.021 -0.038 -0.014]
# state[0] - позиция тележки
# state[1] - скорость тележки
# state[2] - угол отклонения шеста от вертикали в радианах
# state[3] - скорость изменения угла наклона шеста
steps = 0
done = False
# Начинаем игру
# Цель - как можно дольше не допустить падения шеста
while not done:
if render: env.render() # Графическое отображение симуляции
steps += 1
state = state.reshape(-1, observation_space)
action = q_agent.find_action(state) # Определяем очередное действие - 0 или 1
# Получаем от среды, в которой выполнено действие action, состояние объекта, награду и значение флага завершения игры
# В каждый момент игры, пока не наступило одно из условий ее прекращения, награда равна 1
state_next, reward, done, info = env.step(action)
if done: reward = -reward
# Запоминаем предыдущее состояние объекта, действие, награду за это действие, текущее состояние и значение done
q_agent.history.append((state[0], action, reward, state_next, done))
state = state_next # Обновляем текущее состояние
#
q_agent.replay(batch_size) # Обучение агента после каждого шага
# done становится равным True, когда завершается игра, например, отклонение угла превысило допустимое значение
if ep % 10 == 0:
print('Эпизод: %d число шагов: %d eps: %.3f' % (ep, steps, q_agent.eps))
Задания.
REINFORCE является алгоритмом градиента стратегии (ГС). В методах ГС для максимизации целевой функции ценности состояний J(θ) используется ее градиент. В приводимом примере целевая функция аппроксимируется НС, и градиент применяется для корректировки ее весов в результате обратного распространения ошибки. Способ вычисления ошибки (потерь) следует из теоремы о градиенте стратегии [7].
REINFORCE - это алгоритм с единой стратегией. В подобных алгоритмах не используется прошлый опыт: весь опыт, накопленный при следовании текущей стратегии, отбрасывается, после перехода к другой стратегии.
Оптимизация стратегии выполняется на пакете данных, сформированном на основании только что реализованной и сохраненной в буфере траектории. Пакет включает все ее переходы.
Процедура оптимизации заключается в обновлении весов НС в результате обратного распространения ошибки, полученной на обучающем пакете данных.
В приводимом ниже примере потери вычисляются следующим образом (приводятся код и распечатка значений переменных):
import numpy as np
import tensorflow as tf
def mlp(x, hidden_layers, output_size, activation = tf.nn.relu, last_activation = None):
d = tf.keras.layers.Dense # Многслойный перцептрон
for l in hidden_layers:
x = d(units = l, activation = activation)(x)
return d(units = output_size, activation = last_activation)(x)
act_dim = 2
#tf.enable_eager_execution()
#tf.set_random_seed(22)
np.random.seed(22)
obs_ph = np.random.uniform(1, 10, 8).reshape(2, 4) # Задаем (произвольно) состояния, действия и награды
act_ph = np.array([1, 0])
ret_ph = np.array([3.0, 2.0])
p_logits = mlp(obs_ph, [256, 64], act_dim, activation = tf.tanh) # Выход НС ; shape=(2, 2)
rc = tf.random.categorical(p_logits, 1) # shape=(2, 1)
act_multn = tf.squeeze(rc) # shape=(2,)
actions_mask = tf.one_hot(act_ph, depth = act_dim) # (shape=(2, 2)
sfm = tf.nn.log_softmax(p_logits) # (shape=(2, 2)
p_log = tf.reduce_sum(actions_mask * sfm, axis = 1) # Применяем маску; shape=(2,)
p_loss = -tf.reduce_mean(p_log * ret_ph) # Скалярные потери; shape=()
print(obs_ph) # [[2.87 5.33 4.78 8.73] [2.54 4.04 3.43 7.21]]
print(p_logits.numpy()) # [[0.028 -0.13] [0.08 -0.12]]
print(rc.numpy()) # [[1] [1]]
print(act_multn.numpy()) # [1 1]
print(actions_mask.numpy()) # [[0. 1.] [1. 0.]]
print(sfm.numpy()) # [[-0.61 -0.77] [-0.59 -0.81]]
# actions_mask * sfm: [[-0. -0.77] [-0.59 -0.]]
print(p_log.numpy()) # [-0.77 -0.59]
# p_log * ret_ph: [-2.33 -1.18]
print(p_loss.numpy()) # 1.76
Для вычисления потерь берется вся траектория (множество состояний, действий и наград одного эпизода). Награды определяются с учетом обесценивания (см. функцию discounted_rewards).
Потери, используемые для оптимизации стратегии, вычисляются следующим образом:
Эти действия выполняем для каждого элемента текущей траектории, после чего получаем потери как среднее значений sum_ret.
Пример.
Важно: награды перед записью в буфер подвергаются преобразованию (см. функцию discounted_rewards).
discounted_rewards:
Вход:
rews: [1., 1., 1., 1., 1.]
gamma: 0.5
Выход:
rtg: [1.9375 1.875 1.75 1.5 1.]
Полученные потери используются для вычисления градиентов и последующего обновления весов НС.
Действия выполняются после завершения (по флажку done) каждого эпизода.
Приводятся две реализации алгоритма: с базой (use_base = True) и без нее.
База, как известно [7], способствует снижению дисперсии вознаграждения (стратегия стохастическая, и каждое ее выполнение обеспечивает в общем случае разные вознаграждения).
import numpy as np
import tensorflow.compat.v1 as tf
import gym
import time
from sys import exit
render = False
use_base = True
def mlp(x, hidden_layers, output_size, activation = tf.nn.relu, last_activation = None):
d = tf.keras.layers.Dense # Многслойный перцептрон
for l in hidden_layers:
x = d(units = l, activation = activation)(x)
return d(units = output_size, activation = last_activation)(x)
def discounted_rewards(rews, gamma): # Награды на текущей траектории с учетом обесценивания
# rews: список наград
# gamma: коэффициент ообесценивания
rtg = np.zeros_like(rews, dtype = np.float32)
rtg[-1] = rews[-1]
for i in reversed(range(len(rews) - 1)):
rtg[i] = rews[i] + gamma * rtg[i + 1]
# Пример
# rews: [1., 1., 1., 1., 1.]
# gamma: 0.5
# rtg: [1.9375 1.875 1.75 1.5 1.]
return rtg
class Buffer():
# Накопитель результатов опытов одного эпизода
# Дина буфера не превосходит steps_per_epoch
def __init__(self, gamma = 0.99):
self.gamma = gamma
self.obs = [] # Наблюдения, действия и награды в одном эпизоде
self.act = [] # Инициализация в начале каждого эпизода
self.ret = []
if use_base: self.rtg = []
def store(self, temp_traj):
# Добавляем temp_traj в буфер и вычисляем пеимущество и награды
# temp_traj: список массивов вида (состояние, награда, действие)
# Длина промежуточной траектории (не более 500 в случае CartPole)
if len(temp_traj) > 0:
obs, act, rew, val = [], [], [], []
for s in temp_traj:
obs.append(s[0])
rew.append(s[1])
act.append(s[2])
if use_base: val.append(s[3])
self.obs.extend(obs)
rtg = discounted_rewards(rew, self.gamma)
if use_base: # ret = G - V
self.rtg.extend(rtg)
rtg = rtg - val
self.ret.extend(rtg)
self.act.extend(act)
def get_batch(self):
if use_base:
return self.obs, self.act, self.ret, self.rtg
else:
return self.obs, self.act, self.ret
def __len__(self):
assert(len(self.obs) == len(self.act) == len(self.ret))
return len(self.obs)
def REINFORCE(env_name, hidden_sizes=[32], lr=5e-3, num_epochs=50, gamma=0.99, steps_per_epoch=100):
'''
Реализация алгоритма REINFORCE
env_name: имя среды
hidden_size: список с числом нейронов на скрытых слоях НС
lr: скорость обучения стратегии (см. Adam)
gamma: коэффициент обесценивания награды
steps_per_epoch: число шагов в эпохе (эпизоде)
num_epochs: число эпох
'''
tf.reset_default_graph() # Граф вычислений
env = gym.make(env_name)
obs_dim = env.observation_space.shape # (4, )
act_dim = env.action_space.n # 2
# Местодержатели состояний, действий и наград
obs_ph = tf.placeholder(shape=(None, obs_dim[0]), dtype = tf.float32, name = 'obs')
act_ph = tf.placeholder(shape=(None,), dtype = tf.int32, name = 'act')
ret_ph = tf.placeholder(shape=(None,), dtype = tf.float32, name = 'ret')
if use_base:
# Местодержатель предстоящего вознаграждения
rtg_ph = tf.placeholder(shape=(None,), dtype=tf.float32, name='rtg')
# Функция ценности, аппроксимируемая многослойным перцептроном
s_values = tf.squeeze(mlp(obs_ph, hidden_sizes, 1, activation=tf.tanh))
# Функция потерь – СКО
v_loss = tf.reduce_mean((rtg_ph - s_values)**2)
# Оптимизация (обучение) функции ценности
v_opt = tf.train.AdamOptimizer(lr).minimize(v_loss)
# Стратегия (действия)
p_logits = mlp(obs_ph, hidden_sizes, act_dim, activation = tf.tanh) # (None, 2)
rc = tf.random.categorical(p_logits, 1) # (None, 1)
act_multn = tf.squeeze(rc) # [1 1 0 ...] # Действия
# Потери
actions_mask = tf.one_hot(act_ph, depth = act_dim) # (None, 2)
sfm = tf.nn.log_softmax(p_logits) # (None, 2)
p_log = tf.reduce_sum(actions_mask * sfm, axis = 1) # (None)
p_loss = -tf.reduce_mean(p_log * ret_ph) # Скалярные потери
# Оптимизация (обучение) стратегии - корректировка весов НС
# в реузльтате обратного распространения ошибки
p_opt = tf.train.AdamOptimizer(lr).minimize(p_loss)
print('Начало обучения')
sess = tf.Session() # Создаем сессию и инициализируем параметры
sess.run(tf.global_variables_initializer())
step_count = 0
train_rewards = [] # Награды эпох между промежуточной печатью
train_ep_len = [] # Число шагов в эпохах между промежуточной печатью
timer = time.time()
for ep in range(num_epochs): # Главный цикл
obs = env.reset() # Иницииализация среды, буфера, переменных
buffer = Buffer(gamma)
env_buf, ep_rews = [], []
while len(buffer) < steps_per_epoch:
if render: env.render()
# Реализация стратегии. Действие act - это 1 или 0 (в случае CartPole)
if use_base:
# Помимо act_multn, вычисляем s_values
act, val = sess.run([act_multn, s_values], feed_dict={obs_ph:[obs]})
else:
act = sess.run(act_multn, feed_dict = {obs_ph:[obs]}) # 1 или 0
# Шаг в среде
step_count += 1
obs2, rew, done, _ = env.step(act) # np.squeeze(act)
# Пополнение буфера (истории опытов эпизода)
if use_base:
# Включаем дополнительно предсказание ценности состояния
env_buf.append([obs.copy(), rew, act, val]) # np.squeeze(val)
else:
env_buf.append([obs.copy(), rew, act])
obs = obs2.copy()
ep_rews.append(rew)
if done:
buffer.store(env_buf) # Сохраняем завершенную траекторию
train_rewards.append(np.sum(ep_rews)) # и сведения о наградах эпизода
train_ep_len.append(len(ep_rews))
obs = env.reset() # Перезагрузка среды
env_buf, ep_rews = [], []
if use_base: # Пакеты из буфера
obs_batch, act_batch, ret_batch, rtg_batch = buffer.get_batch()
feed_dict = {obs_ph:obs_batch, act_ph:act_batch, ret_ph:ret_batch, rtg_ph:rtg_batch}
else:
obs_batch, act_batch, ret_batch = buffer.get_batch()
feed_dict = {obs_ph:obs_batch, act_ph:act_batch, ret_ph:ret_batch}
sess.run(p_opt, feed_dict = feed_dict) # Оптимизация стратегии
if ep % 10 == 0:
# Изъято: Всего шагов:%d - step_count, Число шагов:%d - np.mean(train_ep_len),
print('Эпизод:%d Награда. средняя:%.0f максимальная:%.0f Размер буфера:%d t:%d'
% (ep, np.mean(train_rewards), np.max(train_rewards), len(buffer), time.time()-timer))
timer = time.time()
train_rewards = []
train_ep_len = []
env.close()
if add_summary: file_writer.close()
tf.disable_eager_execution() # Добавлено
if __name__ == '__main__':
env_name = 'CartPole-v1'
REINFORCE(env_name, hidden_sizes = [64], lr = 8e-3, gamma = 0.99,
num_epochs = 1000, steps_per_epoch = 1000)
Задание.
Реализовать алгоритм, используя Tensorflow, Keras и tf.GradientTape().
Исполнитель-Критик, как и REINFORCE, - это алгоритм градиента стратегии.
В приводимом примере Исполнитель - это стратегия (предсказывает действие), а критик аппроксимирует функцию ценности состояний.
Цель критика – стимулировать исполнителя вырабатывать действия, максимизирующие доход агента. Это достигается за счет соответствующего вычисления потерь Исполнителя и Критика.
Обучение ведется по законченной траектории. Затем история очищается.
Критик предсказывает value будущую суммарную награду в эпизоде.
Исполнитель должен предсказывать действие, приводящее к награде, близкой к прогнозу критика:
diff = ret - value
Потери Исполнителя: -log_prob * diff, где log_prob - логарифм вероятности выбора действия
Пример.
Критик должен обновляться так, чтобы лучше оценивать будущие награды.
Потери Критика: huber_loss(value, ret).
huber_loss - квадратична для малых значений и линейна для больших.
При обратном распространении ошибки берем суммму потерь Исполнителя и Критика.
loss_value = sum(actor_losses) + sum(critic_losses),
где actor_losses и critic_losses - списки потерь Исполнителя и Критика в текущем эпизоде
Важно: потери returns определяются по rewards_history (см. код ниже).
Пример.
# https://www.tensorflow.org/tutorials/reinforcement_learning/actor_critic
# И-К представлены одной НС с двумя выходами - прогнозы Исполнителя и Критика
from sys import exit
import gym
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
render = False
show_model = False
seed = 42
gamma = 0.99 # Коэффициент обесценивания награды
env = gym.make('CartPole-v1')
env.reset(seed = seed)
# Наименьшее число, такое, что 1.0 + eps != 1.0
eps = np.finfo(np.float32).eps.item()
num_inputs = 4
num_actions = env.action_space.n # 2
num_hidden = 128
inputs = layers.Input(shape=(num_inputs,))
common = layers.Dense(num_hidden, activation = 'relu')(inputs)
action = layers.Dense(num_actions, activation = 'softmax')(common)
critic = layers.Dense(1)(common)
model = keras.Model(inputs = inputs, outputs = [action, critic])
if show_model: model.summary()
optimizer = keras.optimizers.Adam(learning_rate = 0.01)
huber_loss = keras.losses.Huber()
action_probs_history, critic_value_history, rewards_history = [], [], []
total_episodes = 200
print('Всего эпизодов:', total_episodes)
ep_reward_list = [] # История наград
for ep in range(total_episodes): # Цикл обучения
state = env.reset()
ep_reward = 0
with tf.GradientTape() as tape:
while True: # Выход по done
if render: env.render()
state = tf.convert_to_tensor(state)
state = tf.expand_dims(state, 0)
# Прогноз вероятностей действий и оценка будущих наград
# по состоянию среды state
action_probs, critic_value = model(state)
# Случайный выбор действия с учетом вероятностей action_probs
action = np.random.choice(num_actions, p = np.squeeze(action_probs))
log_prob = tf.math.log(action_probs[0, action])
# Применяем выбраное действие
state, reward, done, _ = env.step(action)
# action_probs: [0.496 0.504]
# critic_value: [[0.015]]
# action: 0
# state: [-0.04 -0.15 0.03 0.33]
# reward: 1.0
# done: False
#
action_probs_history.append(log_prob) # Пишем историю
critic_value_history.append(critic_value[0, 0])
rewards_history.append(reward)
#
ep_reward += reward
if done: break
ep_reward_list.append(ep_reward)
# Награды с учетом обесценивания. Используются в качестве меток для критика
# Получаем убывающий список наград (см. функцию discounted_rewards, REINFORCE)
returns = []
discounted_sum = 0
for r in rewards_history[::-1]:
discounted_sum = r + gamma * discounted_sum
returns.insert(0, discounted_sum)
# Нормализация
returns = np.array(returns)
returns = (returns - np.mean(returns)) / (np.std(returns) + eps)
returns = returns.tolist()
# Потери для обновления НС
history = zip(action_probs_history, critic_value_history, returns)
actor_losses = []
critic_losses = []
for log_prob, value, ret in history: # ret - суммарная награда
# Критик предсказывает будущую суммарную награду
# Исполнитель должен предсказывать действие, приводящее к награде,
# близкой к прогнозу критика
diff = ret - value
actor_losses.append(-log_prob * diff) # Потери исполнителя
# log_prob: -0.704 - логарифм вероятности выбора действия
# ret: 1.556
# value: 0.005 - оценка ценности состояния, выполненная критиком
# diff: 1.551
# Критик должен обновляться так, чтобы лучше оценивать будущие награды
critic_losses.append( # Потери критика
huber_loss(tf.expand_dims(value, 0), tf.expand_dims(ret, 0)))
# huber_loss - квадратична для малых значений и линейна для больших
# Обратное распространение ошибки
loss_value = sum(actor_losses) + sum(critic_losses)
grads = tape.gradient(loss_value, model.trainable_variables)
optimizer.apply_gradients(zip(grads, model.trainable_variables))
action_probs_history.clear() # Чистим историю
critic_value_history.clear()
rewards_history.clear()
if ep % 10 == 0:
template = "Эпизод {}; награда: {:.1f}"
print(template.format(ep, ep_reward))
# График истории обучения
plt.plot(ep_reward_list)
plt.xlabel('Эпизод')
plt.ylabel('Награда')
plt.show()
PPO (проксимальная оптимизация стратегии), так же как и TRPO, пытается найти и сделать наибольший шаг оптимизации стратегии, используя текущие данные, не приводящий к срыву процесса оптимизации.
TRPO решает эту задачу, употребляя метод с вычислительной сложностью второго порядка, а PPO - первого. Новая стратегия при этом оказывается близкой к прежней.
PPO реализуется проще TRPO, не уступая последнему по эффективности.
Известны два варианта PPO: PPO-Penalty и PPO-Clip [8].
PPO-Clip обрезает целевую функцию, препятствуя тем самым серьезному удалению новой стратегии от старой (см. функцию train_policy [9]).
# https://keras.io/examples/rl/ppo_cartpole/ - код
# https://spinningup.openai.com/en/latest/algorithms/trpo.html - теория
# https://spinningup.openai.com/en/latest/algorithms/ppo.html - теория
from sys import exit
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import gym
import scipy.signal
import time
# Гиперпараметры алгоритма PPO
steps_per_epoch = 4000
epochs = 30
gamma = 0.99
clip_ratio = 0.2
policy_learning_rate = 3e-4
value_function_learning_rate = 1e-3
train_policy_iterations = 80
train_value_iterations = 80
lam = 0.97
target_kl = 0.01 # Для ранней остановки
hidden_sizes = (64, 64)
render = False # Флаг визуализации окружения
def discounted_cumulative_sums(x, discount):
# Дисконтированные накопительные суммы элементов вектора x
# (для вычисления целевых наград и преимущества)
dcs = scipy.signal.lfilter([1], [1, float(-discount)], x[::-1], axis = 0)
# discount: 0.99
# x: [1. 1. 1. 1. 1. 0.]
# x[::-1]: [0. 1. 1. 1. 1. 1.]
# dcs: [0. 1. 1.99 2.97 3.94 4.9]
# dcs[::-1]: [4.9 3.94 2.97 1.99 1. 0.]
return dcs[::-1]
class Buffer:
# Буфер для хранения траекторий
def __init__(self, obs_dims, size, gamma = 0.99, lam = 0.95):
# Инициализация буфера
self.obs_buf = np.zeros((size, obs_dims), dtype = np.float32)
self.action_buf = np.zeros(size, dtype = np.int32)
self.advantage_buf = np.zeros(size, dtype = np.float32)
self.reward_buf = np.zeros(size, dtype = np.float32)
self.return_buf = np.zeros(size, dtype = np.float32)
self.value_buf = np.zeros(size, dtype = np.float32)
self.logprob_buf = np.zeros(size, dtype = np.float32)
self.gamma, self.lam = gamma, lam
self.pointer, self.trajectory_start_index = 0, 0
def store(self, observation, action, reward, value, logprob):
# Добавляем шаг взаимодействия агента со средой
self.obs_buf[self.pointer] = observation
self.action_buf[self.pointer] = action
self.reward_buf[self.pointer] = reward
self.value_buf[self.pointer] = value
self.logprob_buf[self.pointer] = logprob
# observation: [[-0.037 0.007 -0.028 0.003]]
# action: [0]
# reward: 1.0
# value: [-0.028]
# logprob: [-0.688]
self.pointer += 1
def finish_trajectory(self, last_value=0):
# Завершаем траекторию, вычисляя оценку преимущества и целевые награды
path_slice = slice(self.trajectory_start_index, self.pointer)
rewards = np.append(self.reward_buf[path_slice], last_value)
values = np.append(self.value_buf[path_slice], last_value)
deltas = rewards[:-1] + self.gamma * values[1:] - values[:-1]
ab = discounted_cumulative_sums(deltas, self.gamma * self.lam)
rb = discounted_cumulative_sums(rewards, self.gamma)[:-1]
# path_slice: slice(0, 21, None)
# values: [0.0016 0.021 ... -0.048 0.]
# deltas: [1.019 0.979 ... 1.004 1.048]]
# ab: [12.16 11.84 ... 1.99 1.048]
# rewards: [1. 1. ... 1. 1. 0.]
# rb: [19.02 18.20 ... 1.99 1.]
self.advantage_buf[path_slice] = ab
self.return_buf[path_slice] = rb
self.trajectory_start_index = self.pointer
def get(self):
# Нормализует преимущество. Возвращает буфер
self.pointer, self.trajectory_start_index = 0, 0
ab = self.advantage_buf
advantage_mean = np.mean(ab)
advantage_std = np.std(ab)
self.advantage_buf = (ab - advantage_mean) / advantage_std
return self.obs_buf, self.action_buf, ab, \
self.return_buf, self.logprob_buf
def mlp(x, sizes, activation = tf.tanh, output_activation = None):
for size in sizes[:-1]: # НС прямого распространения
x = layers.Dense(units = size, activation = activation)(x)
return layers.Dense(units = sizes[-1], activation = output_activation)(x)
def logprobabilities(logits, a):
# Вычисляет логарифм вероятности действия, используя выход исполнителя
logprobs_all = tf.nn.log_softmax(logits)
logprob = tf.reduce_sum(tf.one_hot(a, num_actions) * logprobs_all, axis = 1)
return logprob
# Получаем действие исполнителя
@tf.function
def sample_action(observation):
logits = actor(observation)
action = tf.squeeze(tf.random.categorical(logits, 1), axis = 1)
return logits, action # [[-0.001 -0.011]], [0]
# Обучаем стратегию, максимизируя PPO-Clip (обрезанную) целевую функцию
@tf.function
def train_policy(obs_buf, action_buf, logprob_buf, advantage_buf):
with tf.GradientTape() as tape: # Фиксируем операции автоматического дифференцирования
ratio = tf.exp(logprobabilities(actor(obs_buf), action_buf) - logprob_buf)
# ratio: tf.Tensor([1. 1. 1. ... 1. 1. 1.], shape=(4000,), dtype=float32)
min_advantage = tf.where(
advantage_buf > 0,
(1 + clip_ratio) * advantage_buf,
(1 - clip_ratio) * advantage_buf,
)
tf_min = tf.minimum(ratio * advantage_buf, min_advantage)
policy_loss = -tf.reduce_mean(tf_min) # tf.Tensor(-8.22, shape=(), dtype=float32)
policy_grads = tape.gradient(policy_loss, actor.trainable_variables)
policy_opt.apply_gradients(zip(policy_grads, actor.trainable_variables))
kl = logprob_buf - logprobabilities(actor(obs_buf), action_buf)
kl = tf.reduce_sum(tf.reduce_mean(kl))
return kl
# Обучаем функцию ценности, используя СКО (mse)
@tf.function
def train_value_function(obs_buf, return_buf):
with tf.GradientTape() as tape: # Фиксируем операции автоматического дифференцирования
value_loss = tf.reduce_mean((return_buf - critic(obs_buf)) ** 2)
value_grads = tape.gradient(value_loss, critic.trainable_variables)
value_opt.apply_gradients(zip(value_grads, critic.trainable_variables))
# Инициализация среды
# Размеры постранства наблюдений и число возможных действий
env = gym.make('CartPole-v1')
obs_dims = env.observation_space.shape[0] # 4
num_actions = env.action_space.n # 2
buffer = Buffer(obs_dims, steps_per_epoch) # Инициализация буфера
# Инициализация исполнителя и критика как keras-моделей
obs_inp = keras.Input(shape = (obs_dims,), dtype = tf.float32)
logits = mlp(obs_inp, list(hidden_sizes) + [num_actions], tf.tanh, None)
actor = keras.Model(inputs = obs_inp, outputs = logits)
value = mlp(obs_inp, list(hidden_sizes) + [1], tf.tanh, None)
value = tf.squeeze(value, axis = 1)
critic = keras.Model(inputs = obs_inp, outputs = value)
# Инициализация оптимизаторов стратегии и функции ценности
policy_opt = keras.optimizers.Adam(learning_rate = policy_learning_rate)
value_opt = keras.optimizers.Adam(learning_rate = value_function_learning_rate)
observation, episode_return, episode_length = env.reset(), 0, 0
for epoch in range(epochs): # Цикл по эпохам
# Initialize the sum of the returns, lengths and number of episodes for each epoch
sum_return = 0 # Сумммарная награда, длина эпизода, число эпизодов в каждой эпохе
sum_length = 0
num_episodes = 0
for t in range(steps_per_epoch): # Реализация эпохи
if render: env.render()
# Получаем выход НС, действие; выполняем шаг
observation = observation.reshape(1, -1) # [[0.027 0.045 0.018 0.013]]
logits, action = sample_action(observation) # [[-0.001 -0.011]], [0]
# Новое наблюдение
observation_new, reward, done, _ = env.step(action[0].numpy())
episode_return += reward
episode_length += 1
# Величина логарифа вероятности действия
value_t = critic(observation) # [0.001]
logprob_t = logprobabilities(logits, action) # [-0.694]
# Пополняем буфер значениями obs, act, rew, v_t, logp_pi_t
buffer.store(observation, action, reward, value_t, logprob_t)
observation = observation_new
# Завершаем траекторию, если достигли завершающего состояния
if done or (t == steps_per_epoch - 1):
last_value = 0 if done else critic(observation.reshape(1, -1))
buffer.finish_trajectory(last_value)
sum_return += episode_return
sum_length += episode_length
num_episodes += 1
observation, episode_return, episode_length = env.reset(), 0, 0
# Получаем значения из буфера
obs_buf, action_buf, advantage_buf, return_buf, logprob_buf = buffer.get()
# obs_buf: [[0.031 0.032 0.036 -0.026] [0.031 -0.162 0.035 0.277] ...]
# action_buf: [0 0 1 ... 0 0 1]
# advantage_buf: [12.6 12.3 11.9 ...]
# return_buf: [20.6 19.8 19.0 ...]
# logprob_buf: [-0.695 -0.764 -0.569 ...]
# Обновляем стратегию и реализуем раннюю остановку, используя расстояние Кульбака_Лейбнера
for _ in range(train_policy_iterations):
kl = train_policy(obs_buf, action_buf, logprob_buf, advantage_buf)
# kl: 7.769e-05
if kl > 1.5 * target_kl: break # Ранняя остановка
# Обновляем функцию ценности
for _ in range(train_value_iterations):
train_value_function(obs_buf, return_buf)
avg_r = round(sum_return / num_episodes, 1)
avg_l = round(sum_length / num_episodes, 1)
print(f'Эпоха: {epoch + 1}. Средняя награда: {avg_r}. Средняя длина: {avg_l}')
Обучение и обновление НС выполняется на каждом шаге (как в DQN)
При управлении перевернутым маятником действием является вращающий момент, действующий на маятник по часовой или против часовой стрелки. Диапазон изменения момента - [-2.0, 2.0].
DDPG (глубокий детерминированный градиент стратегии) - это алгоритм, комбинирующий идеи DPG (Deterministic Policy Gradient) и DQN (Deep Q-Network).
В DDPG две НС:
1. Исполнитель - генерирует действие, получив состояние.
2. Критик - генерирует, получив состояние и действие, положительное число, если действие хорошее, и отрицательное - в противном случае.
В отличие от DQN, DDPG, кроме базовых Исполнителя и Критика, использует две целевые НС - одну для Исполнителя, другую для Критика.
Веса этих НС мягко обновляются по весам базовых моделей, что позволяет отчасти стабилизировать целевые значения, используемые для обучения базовых НС.
Обучение базовых НС производится по случайной выборке опытов из буфера заданного размера.
Если число опытов в буфере превышает его размер, то новый опыт замещает старый [10].
Целевые НС употребляются для определения потерь Критика. Цель обучения Критика вычисляется как в DQN.
Потери исполнителя - это усредненный выход критика, взятый с отрицательным знаком.
# https://keras.io/examples/rl/ddpg_pendulum/
from sys import exit
import gym
import tensorflow as tf
from tensorflow.keras import layers
import numpy as np
import matplotlib.pyplot as plt
render = False
show_model = False
# Чтобы повысить эффективность Исполнителя, используется зашумление
# Шум создается как Ornstein-Uhlenbeck процесс
class OUActionNoise:
def __init__(self, mean, std_deviation, theta=0.15, dt=1e-2, x_initial=None):
self.theta = theta
self.mean = mean
self.std_dev = std_deviation
self.dt = dt
self.x_initial = x_initial
self.reset()
# Вызывается при каждом обращении к ou_noise
# ou_noise = OUActionNoise(...)
def __call__(self):
# См. https://www.wikipedia.org/wiki/Ornstein-Uhlenbeck_process
x = self.x_prev + self.theta * (self.mean - self.x_prev) * self.dt + \
self.std_dev * np.sqrt(self.dt) * np.random.normal(size=self.mean.shape)
# Сохраняем x в x_prev и делаем следующий шум зависимым от текущего
self.x_prev = x
return x
def reset(self):
if self.x_initial is not None:
self.x_prev = self.x_initial
else:
self.x_prev = np.zeros_like(self.mean)
class Buffer:
def __init__(self, buffer_capacity = 100000, batch_size = 64):
self.buf_capacity = buffer_capacity # Предельное число хранимых опытов
self.batch_size = batch_size # Размер обучающего пакета
self.buf_cnt = 0 # Число вывзовов record()
# Массивы буфера
self.state_buffer = np.zeros((self.buf_capacity, num_states))
self.action_buffer = np.zeros((self.buf_capacity, num_actions))
self.reward_buffer = np.zeros((self.buf_capacity, 1))
self.next_state_buffer = np.zeros((self.buf_capacity, num_states))
def record(self, obs_tuple): # На входе кортеж (s, a, r, s')
# Следим, чтобы index < self.buf_capacity
index = self.buf_cnt % self.buf_capacity
self.state_buffer[index] = obs_tuple[0]
self.action_buffer[index] = obs_tuple[1]
self.reward_buffer[index] = obs_tuple[2]
self.next_state_buffer[index] = obs_tuple[3]
self.buf_cnt += 1
# Быстрое исполнение задано в TensorFlow 2 по умолчанию
# Декоратор tf.function позволяет TensorFlow строить статический граф вычислений,
# исходя из логики задаваемой функции. Это ускоряет вычисление блоков кода
# с малым числом операций TensorFlow
@tf.function
def update(self, state_batch, action_batch, reward_batch, next_state_batch):
# Обучение НС Исполнителя и Критика
# Получаем целевое значение, затем выход Критика и его потери
with tf.GradientTape() as tape:
target_actions = target_actor(next_state_batch, training = True)
# Цель обучения Критика (как в DQN)
y = reward_batch + gamma * target_critic(
[next_state_batch, target_actions], training = True
)
critic_value = critic_model([state_batch, action_batch], training = True)
critic_loss = tf.math.reduce_mean(tf.math.square(y - critic_value))
# Вычисляем градиенты Критика и обновляем его веса
critic_grad = tape.gradient(critic_loss, critic_model.trainable_variables)
critic_optimizer.apply_gradients(
zip(critic_grad, critic_model.trainable_variables))
# Исполнитель
with tf.GradientTape() as tape:
actions = actor_model(state_batch, training = True)
critic_value = critic_model([state_batch, actions], training = True)
# Потери Исполнителя: -value. Исполнитель обучается генерировать
# действия, снижающие выход Критика
actor_loss = -tf.math.reduce_mean(critic_value)
# Вычисляем градиенты Исполнителя и обновляем его веса
actor_grad = tape.gradient(actor_loss, actor_model.trainable_variables)
actor_optimizer.apply_gradients(
zip(actor_grad, actor_model.trainable_variables))
def learn(self): # Вычисляем потери и обновляем параметры НС
record_range = min(self.buf_cnt, self.buf_capacity)
# Случайные индексы. Возможны повторы
batch_indices = np.random.choice(record_range, self.batch_size)
# Преобразование в тензоры
state_batch = tf.convert_to_tensor(self.state_buffer[batch_indices])
action_batch = tf.convert_to_tensor(self.action_buffer[batch_indices])
reward_batch = tf.convert_to_tensor(self.reward_buffer[batch_indices])
reward_batch = tf.cast(reward_batch, dtype=tf.float32)
next_state_batch = tf.convert_to_tensor(self.next_state_buffer[batch_indices])
self.update(state_batch, action_batch, reward_batch, next_state_batch)
# Мягкое обновление весов целевой НС tau << 1
@tf.function
def update_target(target_weights, weights, tau):
for (a, b) in zip(target_weights, weights):
a.assign(b * tau + a * (1 - tau))
def get_actor(): # Выход Исполнителя
# Начльные веса между -0.003 и 0.003
last_init = tf.random_uniform_initializer(minval = -0.003, maxval = 0.003)
inp = layers.Input(shape = (num_states,))
x = layers.Dense(256, activation = 'relu')(inp)
x = layers.Dense(256, activation = 'relu')(x)
out = layers.Dense(1, activation = 'tanh', kernel_initializer=last_init)(x)
out = out * upper_bound # Pendulum: upper bound = 2.0
model = tf.keras.Model(inp, out)
return model
def get_critic(): # Выход Критика
# Первый вход НС - это состояние
state_inp = layers.Input(shape = (num_states))
x = layers.Dense(16, activation = 'relu')(state_inp)
state_out = layers.Dense(32, activation = 'relu')(x)
# Второй вход НС - это действие
action_inp = layers.Input(shape = (num_actions))
action_out = layers.Dense(32, activation = 'relu')(action_inp)
# Конкатенация состояния и действия после их преобразованния с использованием Dense
concat = layers.Concatenate()([state_out, action_out])
x = layers.Dense(256, activation = 'relu')(concat)
x = layers.Dense(256, activation = 'relu')(x)
out = layers.Dense(1)(x)
# Получив преобразованные состояние + действие, генерируем на выходе одно значение
model = tf.keras.Model([state_inp, action_inp], out)
return model
def policy(state, noise_object):
sampled_actions = tf.squeeze(actor_model(state))
noise = noise_object()
# Добавляем шум к действию
sampled_actions = sampled_actions.numpy() + noise
# Значение действия не должно выходить за пределы границ
legal_action = np.clip(sampled_actions, lower_bound, upper_bound)
return [np.squeeze(legal_action)]
env_name = 'Pendulum-v1'
env = gym.make(env_name)
num_states = env.observation_space.shape[0] # 3
num_actions = env.action_space.shape[0] # 1
upper_bound = env.action_space.high[0] # 2 (максимальное и минимальное значения действия)
lower_bound = env.action_space.low[0] # -2
# Гиперпараметры обучения
std_dev = 0.2
ou_noise = OUActionNoise(mean = np.zeros(1), std_deviation = std_dev * np.ones(1))
actor_model = get_actor()
critic_model = get_critic()
if show_model: actor_model.summary()
if show_model: critic_model.summary()
target_actor = get_actor()
target_critic = get_critic()
# Изначально веса целевой и базовой НС соовпадают
target_actor.set_weights(actor_model.get_weights())
target_critic.set_weights(critic_model.get_weights())
# Скорости обучения Исполнителя и Критика
actor_lr = 0.001
critic_lr = 0.002
critic_optimizer = tf.keras.optimizers.Adam(critic_lr)
actor_optimizer = tf.keras.optimizers.Adam(actor_lr)
total_episodes = 100
gamma = 0.99 # Кооэффицииент обесценивания будущих наград
tau = 0.005 # Коэффициент мягкого обновления весов целевых НС
buffer = Buffer(50000, 64)
ep_reward_list = [] # История наград
for ep in range(total_episodes): # Цикл обучения
prev_state = env.reset()
ep_reward = 0
while True:
if render: env.render() # Не использовать в Python ноутбуке
tf_prev_state = tf.expand_dims(tf.convert_to_tensor(prev_state), 0)
action = policy(tf_prev_state, ou_noise) # ou_noise(): [-0.02415974]
# Выполняем действие и получаем состояние, награду, флаг завершения и пр.
state, reward, done, info = env.step(action)
buffer.record((prev_state, action, reward, state))
ep_reward += reward
buffer.learn()
update_target(target_actor.variables, actor_model.variables, tau)
update_target(target_critic.variables, critic_model.variables, tau)
if done: break # Завершаем эпизод по done
prev_state = state
ep_reward_list.append(ep_reward)
print('Эпизод: {} Награда {}'.format(ep, ep_reward))
# График истории обучения
plt.plot(ep_reward_list)
plt.xlabel('Эпизод')
plt.ylabel('Награда')
plt.show()
В двойном Q-обучении с целью преодоления чрезмерного роста Q-значений используются две НС.
Если переменная no_tau = False, то создаются две следующие НС [12]:
Обучается только базовая НС.
Параметры целевой НС устанавливаются по значениям параметров базовой НС.
Второй вариант реализуется, если no_tau = True. Так же создаются две НС. Обе они обучаются.
Первая используется для выбора действия, и обе – для вычисления значений Q-функции [12].
# https://github.com/cyoon1729/deep-Q-networks/blob/master/doubleDQN/clipped_ddqn.py
# https://github.com/cyoon1729/deep-Q-networks/blob/master/doubleDQN/ddqn.py
from sys import exit
import gym
import torch, torch.nn as nn
import torch.nn.functional as F
import numpy as np
import random
from collections import deque
no_tau = not True
class Buffer:
def __init__(self, max_size):
self.buffer = deque(maxlen = max_size)
def push(self, state, action, reward, next_state, done):
self.buffer.append((state, action, np.array([reward]), next_state, done))
def sample_batch(self, batch_size):
states, actions, rewards, next_states, dones = [], [], [], [], []
batch = random.sample(self.buffer, batch_size)
for state, action, reward, next_state, done in batch:
states.append(state)
actions.append(action)
rewards.append(reward)
next_states.append(next_state)
dones.append(done)
return states, actions, rewards, next_states, dones
def __len__(self):
return len(self.buffer)
def train_on_batches(env, agent, max_episodes, max_steps, batch_size):
episode_rewards = []
for episode in range(max_episodes):
state = env.reset() # [-0.009 -0.019 -0.014 0.04]
episode_reward = 0
for step in range(max_steps):
action = agent.get_action(state) # 0 или 1
next_state, reward, done, _ = env.step(action)
agent.replay_buffer.push(state, action, reward, next_state, done)
episode_reward += reward
if len(agent.replay_buffer) > batch_size:
agent.update_on_batch(batch_size)
if done or step == max_steps-1:
episode_rewards.append(episode_reward)
if episode % 50 == 0:
print('Эпизод', episode, 'Награда', episode_reward, 'eps =', round(agent.eps, 3))
break
state = next_state
return episode_rewards
class DQN(nn.Module):
def __init__(self, input_dim, output_dim):
super(DQN, self).__init__()
self.input_dim = input_dim
self.output_dim = output_dim
self.fc = nn.Sequential(
nn.Linear(self.input_dim[0], 256),
nn.ReLU(),
nn.Linear(256, 64),
nn.ReLU(),
nn.Linear(64, self.output_dim))
def forward(self, state):
qvals = self.fc(state)
return qvals
class DQNAgent:
def __init__(self, env, learning_rate=3e-4, gamma=0.99, buffer_size=10000):
self.env = env
self.eps = 1.0
self.eps_decay = 0.999
self.eps_min = 0.001
if not no_tau: self.tau = 0.01
self.learning_rate = learning_rate
self.gamma = gamma
self.replay_buffer = Buffer(max_size = buffer_size)
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
input_dim = env.observation_space.shape # (4, )
output_dim = env.action_space.n # 2
self.model = DQN(input_dim, output_dim).to(self.device)
self.optimizer = torch.optim.Adam(self.model.parameters())
if no_tau:
self.model2 = DQN(input_dim, output_dim).to(self.device)
self.optimizer2 = torch.optim.Adam(self.model2.parameters())
else:
self.target_model = DQN(input_dim, output_dim).to(self.device)
# При сознании НС их параметры одинаковы
for target_param, param in zip(self.model.parameters(), self.target_model.parameters()):
target_param.data.copy_(param)
def get_action(self, state):
if np.random.randn() < self.eps:
return self.env.action_space.sample() # 0 или 1
else:
state = torch.FloatTensor(state).float().unsqueeze(0).to(self.device)
q_values = self.model.forward(state)
action = np.argmax(q_values.cpu().detach().numpy())
return action
def compute_loss(self, batch):
states, actions, rewards, next_states, dones = batch
states = torch.FloatTensor(np.array(states)).to(self.device)
actions = torch.LongTensor(actions).to(self.device)
rewards = torch.FloatTensor(np.array(rewards)).to(self.device)
next_states = torch.FloatTensor(np.array(next_states)).to(self.device)
dones = torch.FloatTensor(dones)
actions = actions.view(actions.size(0), 1)
dones = dones.view(dones.size(0), 1)
# Вычисляем потери
curr_Q = self.model.forward(states).gather(1, actions)
if no_tau:
next_Q = self.model.forward(next_states)
curr_Q2 = self.model2.forward(states).gather(1, actions)
next_Q2 = self.model2.forward(next_states)
next_Q = torch.min(torch.max(next_Q, 1)[0], torch.max(next_Q2, 1)[0])
else:
next_Q = self.target_model.forward(next_states)
next_Q = torch.max(next_Q, 1)[0]
next_Q = next_Q.view(next_Q.size(0), 1)
expected_Q = rewards + (1 - dones) * self.gamma * next_Q
loss = F.mse_loss(curr_Q, expected_Q.detach())
if no_tau:
loss2 = F.mse_loss(curr_Q2, expected_Q.detach())
else:
loss2 = None
return loss, loss2
def update_on_batch(self, batch_size):
batch = self.replay_buffer.sample_batch(batch_size)
loss, loss2 = self.compute_loss(batch)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
if no_tau:
self.optimizer2.zero_grad()
loss2.backward()
self.optimizer2.step()
else:
# Обновление весов целевой НС
for target_param, param in zip(self.target_model.parameters(), self.model.parameters()):
target_param.data.copy_(self.tau * param + (1 - self.tau) * target_param)
if self.eps > self.eps_min: self.eps *= self.eps_decay
print('Double DQN.', 'no_tau =', no_tau)
env_id = 'CartPole-v1'
max_episodes = 1000
max_steps = 500
batch_size = 32
env = gym.make(env_id)
agent = DQNAgent(env)
episode_rewards = train_on_batches(env, agent, max_episodes, max_steps, batch_size)
import matplotlib.pyplot as plt
plt.plot(episode_rewards) # График истории обучения
plt.xlabel('Эпизод')
plt.ylabel('Награда')
plt.show()
НС получает состояние и вырабатывает две оценки [13]:
Q-функция определяется следующим образом:
q_values = values + advantages - advantages.mean()
# https://github.com/cyoon1729/deep-Q-networks/tree/master/duelingDQN
from sys import exit
import gym
import torch, torch.nn as nn
import numpy as np
import random
from collections import deque
class DuelingDQN(nn.Module):
def __init__(self, input_dim, output_dim):
super(DuelingDQN, self).__init__()
self.feautures = nn.Sequential(
nn.Linear(input_dim[0], 256),
nn.ReLU(),
nn.Linear(256, 64),
nn.ReLU())
self.values = nn.Sequential(
nn.Linear(64, 32),
nn.ReLU(),
nn.Linear(32, 1))
self.advantages = nn.Sequential(
nn.Linear(64, 32),
nn.ReLU(),
nn.Linear(32, output_dim))
def forward(self, state):
features = self.feautures(state)
values = self.values(features)
advantages = self.advantages(features)
q_values = values + advantages - advantages.mean()
return q_values
class Buffer:
def __init__(self, max_size):
self.buffer = deque(maxlen = max_size)
def push(self, state, action, reward, next_state, done):
self.buffer.append((state, action, np.array([reward]), next_state, done))
def sample_batch(self, batch_size):
states, actions, rewards, next_states, dones = [], [], [], [], []
batch = random.sample(self.buffer, batch_size)
for state, action, reward, next_state, done in batch:
states.append(state)
actions.append(action)
rewards.append(reward)
next_states.append(next_state)
dones.append(done)
return states, actions, rewards, next_states, dones
def __len__(self):
return len(self.buffer)
class DuelingAgent:
def __init__(self, env, learning_rate = 1e-3, gamma = 0.95, buffer_size = 10000):
self.env = env
self.gamma = gamma
self.eps = 1.0
self.eps_decay = 0.999
self.eps_min = 0.001
self.replay_buffer = Buffer(max_size = buffer_size)
self.device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
input_dim = env.observation_space.shape # (4, )
output_dim = env.action_space.n # 2
self.model = DuelingDQN(input_dim, output_dim).to(self.device)
self.optimizer = torch.optim.Adam(self.model.parameters(), lr = learning_rate)
self.MSELoss = nn.MSELoss()
def get_action(self, state):
if np.random.randn() < self.eps:
return self.env.action_space.sample() # 0 или 1
else:
state = torch.FloatTensor(state).float().unsqueeze(0).to(self.device)
q_values = self.model.forward(state)
action = np.argmax(q_values.cpu().detach().numpy())
return action
def compute_loss(self, batch):
states, actions, rewards, next_states, dones = batch
states = torch.FloatTensor(np.array(states)).to(self.device)
actions = torch.LongTensor(actions).to(self.device)
rewards = torch.FloatTensor(np.array(rewards)).to(self.device)
next_states = torch.FloatTensor(np.array(next_states)).to(self.device)
dones = torch.FloatTensor(dones).to(self.device)
curr_Q = self.model.forward(states) # tensor([-0.0691, -0.0197], ...
curr_Q = curr_Q.gather(1, actions.unsqueeze(1)) # tensor([-0.0197], ...
curr_Q = curr_Q.squeeze(1) # tensor(-0.0197, ...
next_Q = self.model.forward(next_states)
max_next_Q = torch.max(next_Q, 1)[0]
expected_Q = rewards.squeeze(1) + (1 - dones) * self.gamma * max_next_Q
loss = self.MSELoss(curr_Q, expected_Q)
return loss
def update_on_batch(self, batch_size):
batch = self.replay_buffer.sample_batch(batch_size)
loss = self.compute_loss(batch)
self.optimizer.zero_grad()
loss.backward()
self.optimizer.step()
if self.eps >= self.eps_min: self.eps *= self.eps_decay
def train_on_batches(env, agent, max_episodes, max_steps, batch_size):
episode_rewards = []
for episode in range(max_episodes):
state = env.reset() # [-0.009 -0.019 -0.014 0.04]
episode_reward = 0
for step in range(max_steps):
action = agent.get_action(state)
next_state, reward, done, _ = env.step(action) # 0 или 1
agent.replay_buffer.push(state, action, reward, next_state, done)
episode_reward += reward
if len(agent.replay_buffer) > batch_size:
agent.update_on_batch(batch_size)
if done or step == max_steps - 1:
episode_rewards.append(episode_reward)
if episode % 50 == 0:
print('Эпизод', episode, 'Награда', episode_reward, 'eps =', round(agent.eps, 3))
break
state = next_state
return episode_rewards
print('Dueling DQN')
env_id = 'CartPole-v1'
max_episodes = 1000
max_steps = 500
batch_size = 32
env = gym.make(env_id)
agent = DuelingAgent(env)
episode_rewards = train_on_batches(env, agent, max_episodes, max_steps, batch_size)
import matplotlib.pyplot as plt
plt.plot(episode_rewards) # График истории обучения
plt.xlabel('Эпизод')
plt.ylabel('Награда')
plt.show()
Библиотека gym предоставляет среды, в которых можно обучать агентов решать следующие задачи [11]:
При использовании PPO (проксимальная стратегия оптимизации) [6], реализованной в stable_baselines, имеем компактный код создания и обучения модели gym, например, шеста на тележке CartPole-v1:
print('Импорт gym')
import gym
##from stable_baselines.ddpg.ddpg import DDPG
print('Импорт MlpPolicy...')
from stable_baselines.common.policies import MlpPolicy
print('Импорт DummyVecEnv')
from stable_baselines.common.vec_env import DummyVecEnv
print('Импорт PPO2')
from stable_baselines import PPO2
#
my_env_id = 'CartPole-v1'
# Получаем среду (окружение)
print('Получаем окружение')
env = gym.make(my_env_id)
# Векторизация окружения (для распараллеливания обучения)
print('Векторизация окружения')
env = DummyVecEnv([lambda: env])
print('Создание модели')
model = PPO2(MlpPolicy, env, verbose = 1)
print('Обучение модели')
model.learn(total_timesteps = 10000)
obs = env.reset()
print('Прогнозирование и воспроизведение результата')
for i in range(1000):
action, _states = model.predict(obs)
obs, rewards, dones, info = env.step(action)
env.render() # Графический вывод
Совершенно так же выглядит stable_baselines-код и для другого объекта gym, например, Humanoid-v2 (mujoco):
import gym
from stable_baselines.ddpg.ddpg import DDPG
from stable_baselines.common.policies import MlpPolicy
from stable_baselines.common.vec_env import DummyVecEnv
from stable_baselines import PPO2
my_env_id = 'Humanoid-v2'
env = gym.make(my_env_id)
env = DummyVecEnv([lambda: env])
model = PPO2(MlpPolicy, env, verbose = 1)
model.learn(total_timesteps = 10000)
obs = env.reset()
for i in range(1000):
action, _states = model.predict(obs)
obs, rewards, dones, info = env.step(action)
if i < 2:
print('i:', i)
print('action:', action)
print('_states', _states)
print('obs:', obs)
print('rewards:', rewards)
print('dones:', dones)
print('info:', info)
env.render()
1. Inverted pendulum. [Электронный ресурс] URL: https://en.wikipedia.org/wiki/Inverted_pendulum (дата обращения: 29.10.2018).
2. Getting Started with Gym. [Электронный ресурс] URL: https://gym.openai.com/docs/ (дата обращения: 29.10.2018).
3. CartPole v0. [Электронный ресурс] URL: https://github.com/openai/gym/wiki/CartPole-v0 (дата обращения: 29.10.2018).
4. Cartpole - Introduction to Reinforcement Learning. [Электронный ресурс] URL: https://towardsdatascience.com/cartpole-introduction-to-reinforcement-learning-ed0eb5b58288 (дата обращения: 29.10.2018).
5. DQN-keras. [Электронный ресурс] URL: https://programmersought.com/article/87216618118/
6. Proximal Policy Optimization. [Электронный ресурс] URL: https://openai.com/blog/openai-baselines-ppo/(дата обращения: 29.10.2018).
7. Лонца А. Алгоритмы обучения с подкреплением на Python. – М.: ДМК Пресс, 2020. – 286 с.
8. PPO. [Электронный ресурс] URL: https://spinningup.openai.com/en/latest/algorithms/ppo.html
9. PPO cartpole. [Электронный ресурс] URL: https://keras.io/examples/rl/ppo_cartpole/
10. DDPG pendulum. [Электронный ресурс] URL: https://keras.io/examples/rl/ddpg_pendulum/
11. Algorithms. [Электронный ресурс] URL: https://gym.openai.com/envs/#algorithmic (дата обращения: 29.10.2018).
12. Double DQN. [Электронный ресурс] URL: https://github.com/cyoon1729/deep-Q-networks/blob/master/doubleDQN/
13. Dueling DQN. [Электронный ресурс] URL: https://github.com/cyoon1729/deep-Q-networks/tree/master/duelingDQN