В задаче коммивояжера ищется кратчайший маршрут между городами, которые коммивояжер должен посетить. В качестве начального может быть выбран любой город. Посетить нужно все заданные города и вернуться в стартовый город. Каждый город посещается единожды, кроме стартового, который коммивояжер посещает в начале и в конце пути.
Когда лучший маршрут найден, стартовым может быть любой его город.
Есть и иные трактовки задачи, например, найти маршрут с минимальной стоимостью.
Тривиальное решение – это перебор всех вариантов, однако такой подход не годится уже при небольшом числе посещаемых городов ввиду неприемлемых вычислительных затрат.
Простейшим решением является употребление жадного алгоритма, суть которого в том, что следующим выбирается город, ближайший к городу нахождения коммивояжера. В общем случае результат далек от оптимального.
В работе рассматривается возможность употребления генетического алгоритма для поиска хорошего решения.
Суть подхода в том, что прежде генерируется множество маршрутов. Это множество называется популяцией. Далее к маршрутам множества применяются операции скрещивания и мутации.
При скрещивании из двух выбранных маршрутов формируется в результате обмена участками маршрута дочерний маршрут.
При мутации меняются местами участки внутри ранее созданного дочернего маршрута.
Приводимый ниже код является модификацией программы, разработанной в 2006 г. Michael LaLena (см. www.lalena.com). Автор программы не возражает против ее некоммерческого использования третьими лицами, например в учебных целях.
Основывается на генетическом алгоритме.
Программа содержит одну форму (рис. 1).
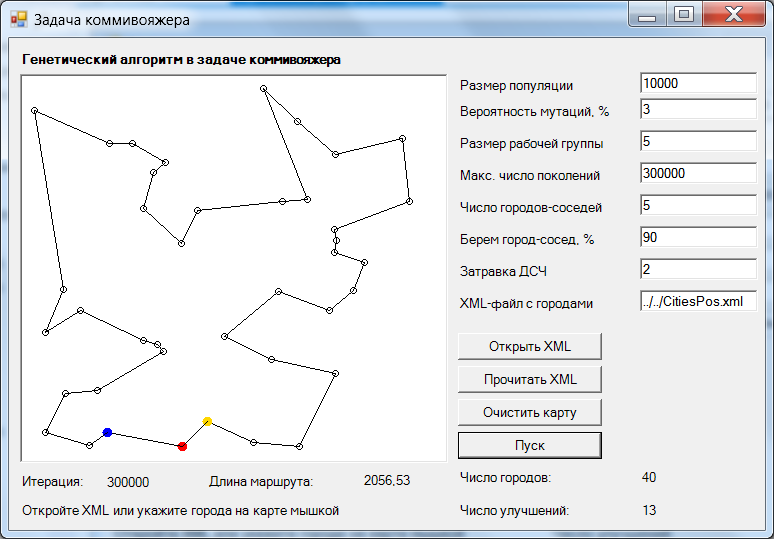
Рис. 1. Форма приложения. Решение найдено
Форма имеет область графического вывода (карту) и позволяет:
Графическая область формы – это объект System.Windows.Forms.PictureBox с именем tourDiagram.
PictureBox может быть выбран и вставлен в форму, например, в результате выполнения следующей цепочки "View–Toolbox–CommonControls–PictureBox". Так же PictureBox можно обнаружить, выполнив "меню Tools–Choose Toolbox Items–вкладка .NET Framework Components–PictureBox".
Для графического вывода создаются следующие объекты:
Далее при выводе лучшего маршрута методами cityGraphics отображаются города в виде окружностей и участки маршрута в виде отрезков прямых линий (см. процедуры DrawTour и DrawCityList).
Визуализация образа выполняется объектом tourDiagram:
tourDiagram.Image = cityImage;
XML-файл содержит перечень координат городов. При отображении на карте используется физическая система координат. Начало координат расположено в верхнем левом углу карты.
Данные в XML-файле должны быть указаны в следующем формате:
<?xml version="1.0" encoding="utf-8" ?>
<CitiesPos>
<CityPos X="160" Y="370"/>
<CityPos X="121" Y="132"/>
…
</CitiesPos>
При чтении файла, если нет ошибок, заполняется список городов, и они отображаются на карте (см. метод OpenCityList).
Элемент списка – это число из диапазона [0, cnt – 1], где cnt – это число городов в маршруте.
Маршрут представляется в виде списка tour номеров городов размера cnt + 1, где cnt - это число посещаемых коммивояжером городов. При этом первый город маршрута (списка) добавляется и в начало, и в конец списка. Это позволяет представить маршрут в виде цепочки городов (рис. 2).

Рис. 2. Представление маршрута в виде цепочки городов. Первый и последний города совпадают: tour[0] = tour[cnt]
Лучший маршрут – это самая короткая цепочка.
Замечание. В программе Michael LaLena [1] использована более сложная модель маршрута: для каждого города указываются его сосед слева и сосед справа. Такая модель усложняет реализацию операций скрещивания и мутации.
Нетрудно заметить, что информация о соседях слева и справа каждого города присутствует и в приведенной на рис. 2 модели. Для первого и последнего городов маршрута (красного и желтого) эта проблема решена за счет дублирования в модели первого (красного) города маршрута.
Популяция – это список маршрутов. Маршрут в списке представляется числом из диапазона [0, populationSize - 1], где populationSize – это размер популяции.
Размер списка постоянен, хотя это и необязательно. Скажем, в популяцию можно добавлять дочерний маршрут, а не заменять им, как это делается в программе, плохой (слишком длинный) маршрут популяции. Можно иметь процедуру чистки популяции, удаляющую время от времени из популяции плохие маршруты и т. д.
Перед созданием начальной популяции для каждого города определяется список closeCities городов-соседей, то есть городов, наиболее близко расположенных к текущему городу. Число городов-соседей у каждого города одинаково и равно numberOfCloseCities.
Элемент списка – это число из диапазона [0, cnt – 1], где cnt – число городов в маршруте. Города в списке упорядочены по возрастанию расстояний городов до текущего города.
Начальная популяция формируется следующим образом:
Сформированная по приведенной схеме модель популяции позволяет довольно просто реализовать операции скрещивания и мутации.
Входные данные.
Выходные данные.
Промежуточные данные.
Алгоритм приводится без многих деталей. Их можно посмотреть в размещенном ниже коде программы.
Реализация алгоритма содержит ряд деталей, которые можно уяснить, просмотрев приводимый ниже код программы.
В программе создаются следующие классы:
Поиск лучшего маршрута и отображение результата на карте городов выполняются в разных нитях.
Решение начинается после нажатия на кнопку "Пуск" (уже создан список городов cityList). Исполняется обработчик StartButton_Click. После выполнения проверок кнопка приобретает надпись "Стоп" и в отдельной нити запускается процедура BeginTsp:
ThreadPool.QueueUserWorkItem(new WaitCallback(BeginTsp));
Процедура BeginTsp после выполнения метода cityList.CalculateCityDistances и создания объекта tsp класса Tsp (tsp = new Tsp();)назначает событию tsp.foundNewBestTour процедуру tsp_foundNewBestTour, которую будет вызывать обработчик этого события. Далее запускается поиск решения: tsp.FindBestTour. После завершения вычислений tsp обнуляется (tsp = null;).
// Создает объект класса Tsp
// Выполняется в отдельной нити
private void BeginTsp(Object stateInfo)
{
// Полагаем, что все данные введены корректно (проверяются в StartButton_Click)
// Находим для каждого города расстояния до всех прочих городов, а также находим его соседей
cityList.CalculateCityDistances(numberOfCloseCities);
tsp = new Tsp();
tsp.foundNewBestTour += new Tsp.NewBestTourEventHandler(tsp_foundNewBestTour);
tsp.FindBestTour(populationSize, maxGenerations, wrGoupSize, mutationChance, seed, chanceUseCloseCity, cityList, numberOfCloseCities);
tsp.foundNewBestTour -= new Tsp.NewBestTourEventHandler(tsp_foundNewBestTour);
tsp = null;
}
Отображение городов и маршрута в графической части формы выполняется процедурой DrawTour. Она запускается при обнаружении очередного лучшего маршрута.
Процедура DrawTour выполняется в отдельной нити, что обеспечивается делегатом DrawEventHandler.
Программа реализована на C# как Windows Form Application.
using System; // Random, InvalidCastException и пр.
using System.Windows.Forms; // PictureBox (tourDiagram), Application (см. класс class Program), MessageBox
using System.Collections.Generic; // Для List
using System.Data; // DataSet, DataRowCollection
using System.Drawing; // Image, Graphics, Point
using System.Threading; // ThreadPool
using System.IO; // FileNotFoundException
namespace Tsp
{
// Класс TspForm управляет формой приложения
public partial class TspForm : Form
{
public int populationSize = 0; // Размер популяции
public int maxGenerations = 0; // Предельное число поколений
public int mutationChance = 0; // Вероятность мутации дочернего маршрута
public int wrGoupSize = 0; // Размер рабочей группы
public int numberOfCloseCities = 0; // Число городов-соседей любого города
public int chanceUseCloseCity = 0; // Вероятность добавления в маршрут города из списка городов-соседей
public int seed = 0; // Затравка датчика случайных чисел
// Список городов, которые должен посетить коммивояжер
Cities cityList = new Cities();
// Tsp – класс, реализующий генетическиий алгоритм решения задачи коммивояжера (tsp-алгоритм)
// Если tsp не null, то задача выполняется
Tsp tsp;
// Образ для отображения городов и маршрута
public Image cityImage;
// Графический объект для образа cityImage
public Graphics cityGraphics;
// Используется отдельная нить, чтобы обновлять карту городов во время вычислений
public delegate void DrawEventHandler(Object sender, TspEventArgs e);
// Стандартный конструктор
public TspForm()
{
InitializeComponent();
}
// tsp-алгоритм порождает событие foundNewBestTour при нахождении текущего лучшего маршрута
// При этом оживляется GUI-нить, что позволяет обновить карту городов
private void tsp_foundNewBestTour(object sender, TspEventArgs e)
{
if (this.InvokeRequired)
{
try
{
this.Invoke(new DrawEventHandler(DrawTour), new object[] { sender, e });
return;
}
catch (Exception) { } // Неудача
}
// Отображаем маршрут
DrawTour(sender, e);
}
// Отображает последний лучший маршрут
// и обновляет поля с числом итераций, длиной маршрута и числом улучшений решения
public void DrawTour(object sender, TspEventArgs e)
{
Tour bestTour = e.BestTour; // Лучший маршрут
cityList = e.CityList;
this.lastFitnessValue.Text = Math.Round(bestTour.Fitness, 2).ToString();
this.lastIterationValue.Text = e.Generation.ToString();
this.NumberOfImprv.Text = e.Imprv.ToString();
int city = bestTour[0];
int nextCity;
cityGraphics.FillRectangle(Brushes.White, 0, 0, cityImage.Width, cityImage.Height);
Point pos;
int cTour = bestTour.Count;
for (int step = 1; step < cTour; step++)
{
pos = cityList[city].Location;
nextCity = bestTour[step];
city = nextCity;
// Отображаем город в виде окружности
// Начальный город маршрута заливаем красным цветом, второй – синим, последний – желтым
if (step == 1) // Окружность начального города маршрута заливаем красным цветом
{
cityGraphics.FillEllipse(Brushes.Red, pos.X - 5, pos.Y - 5, 10, 10);
}
else if (step == 2) // Окружность второго города маршрута заливаем синим цветом
{
cityGraphics.FillEllipse(Brushes.Blue, pos.X - 5, pos.Y - 5, 10, 10);
}
else if (step == cTour - 1) // Окружность предпоследнего города маршрута заливаем желтым цветом
{
cityGraphics.FillEllipse(Brushes.Gold, pos.X - 5, pos.Y - 5, 10, 10);
}
else
{
cityGraphics.DrawEllipse(Pens.Black, pos.X - 3, pos.Y - 3, 6, 6);
}
// Соединяем 2 города линией
cityGraphics.DrawLine(Pens.Black, pos, cityList[nextCity].Location);
}
tourDiagram.Image = cityImage;
if (e.Done)
{
StartButton.Text = "Пуск";
StatusLabel.Text = "Откройте XML или укажите города на карте мышкой";
StatusLabel.ForeColor = Color.Black;
}
}
// Отображает города на растровой карте
private void DrawCityList(Cities cityList)
{
cityImage = new Bitmap(tourDiagram.Width, tourDiagram.Height);
cityGraphics = Graphics.FromImage(cityImage);
foreach (City city in cityList)
{
// Город в виде окружностии
cityGraphics.DrawEllipse(Pens.Black, city.Location.X - 3, city.Location.Y - 3, 6, 6);
}
this.tourDiagram.Image = cityImage;
// Обновляем в форме текстовое поле с числом городов
this.NumberCitiesValue.Text = cityList.Count.ToString();
}
// Запускает или останавливает решение задачи коммивояжера
private void StartButton_Click(object sender, EventArgs e)
{
// Останавливаем нить tsp, если задача решается
if (tsp != null)
{
tsp.Halt = true;
return;
}
try
{
populationSize = Convert.ToInt32(populationSizeTextBox.Text);
maxGenerations = Convert.ToInt32(maxGenerationTextBox.Text);
mutationChance = Convert.ToInt32(mutationTextBox.Text);
wrGoupSize = Convert.ToInt32(groupSizeTextBox.Text);
numberOfCloseCities = Convert.ToInt32(NumberCloseCitiesTextBox.Text);
chanceUseCloseCity = Convert.ToInt32(CloseCityOddsTextBox.Text);
seed = Convert.ToInt32(randomSeedTextBox.Text);
}
catch (FormatException)
{
MessageBox.Show("В полях ввода должны быть числа", "Ошибка", MessageBoxButtons.OK, MessageBoxIcon.Error);
return;
}
string show = "";
bool ok = true;
if (cityList.Count == 0)
{
show = "Список городов пуст"; ok = false;
}
if (ok && cityList.Count < 5)
{
show = "Число городов не может быть меньше, чем 5"; ok = false;
}
if (ok && populationSize <= 0)
{
show = "Укажите размер популяции"; ok = false;
}
if (ok && maxGenerations <= 0)
{
show = "Задайте максимальное число поколений"; ok = false;
}
if (ok && ((mutationChance < 0) || (mutationChance > 100)))
{
show = "Число мутаций должно быть между 0 и 100"; ok = false;
}
if (ok && ((wrGoupSize < 2) || (wrGoupSize > populationSize)))
{
show = "Размер рабочей группы задается между 2 и размером популяций"; ok = false;
}
if (ok && ((numberOfCloseCities < 3) || (numberOfCloseCities >= cityList.Count)))
{
show = "Число городов-соседей для создания начальной популяции должно быть между 3 и числом городов"; ok = false;
}
if (ok && ((chanceUseCloseCity < 0) || (chanceUseCloseCity > 100)))
{
show = "Вероятность использования города-соседа при создании начальной популяции лежит между 0 и 100"; ok = false;
}
if (ok && seed < 0)
{
show = "Затравка датчика случайных чисел не может быть менее нуля"; ok = false;
}
if (!ok)
{
MessageBox.Show(show, "Ошибка", MessageBoxButtons.OK, MessageBoxIcon.Error);
return;
}
this.StartButton.Text = "Стоп";
ThreadPool.QueueUserWorkItem(new WaitCallback(BeginTsp));
}
// Создает объект класса Tsp
// Выполняется в отдельной нити
private void BeginTsp(Object stateInfo)
{
// Полагаем, что все данные введены корректно (проверяются в StartButton_Click)
// Находим для каждого города расстояния до всех прочих городов, а также находим его соседей
cityList.CalculateCityDistances(numberOfCloseCities);
tsp = new Tsp();
tsp.foundNewBestTour += new Tsp.NewBestTourEventHandler(tsp_foundNewBestTour);
tsp.FindBestTour(populationSize, maxGenerations, wrGoupSize, mutationChance, seed, chanceUseCloseCity, cityList, numberOfCloseCities);
tsp.foundNewBestTour -= new Tsp.NewBestTourEventHandler(tsp_foundNewBestTour);
tsp = null;
}
// Выбирает XML-файл с координатами городов
private void selectFileButton_Click(object sender, EventArgs e)
{
OpenFileDialog fileOpenDialog = new OpenFileDialog();
fileOpenDialog.Filter = "XML(*.xml)|*.xml";
fileOpenDialog.InitialDirectory = ".";
fileOpenDialog.ShowDialog();
fileNameTextBox.Text = fileOpenDialog.FileName;
}
// Формируем список городов по XML-файлу
private void openCityListButton_Click(object sender, EventArgs e)
{
string fileName = "";
try
{
if (tsp != null)
{
StatusLabel.Text = "Нельзя изменять список городов во время работы алгоритма";
StatusLabel.ForeColor = Color.Red;
return;
}
fileName = this.fileNameTextBox.Text;
// Читаем файл и формируем список городов
cityList.OpenCityList(fileName);
// Отображаем горрода на карте
this.DrawCityList(cityList);
}
catch (FileNotFoundException)
{
MessageBox.Show("Файл не найден: " + fileName, "Ошибка", MessageBoxButtons.OK, MessageBoxIcon.Error);
}
catch (InvalidCastException)
{
MessageBox.Show("Плохой формат XML-файла", "Ошибка", MessageBoxButtons.OK, MessageBoxIcon.Error);
}
catch
{
MessageBox.Show("Не выбран файл", "Ошибка", MessageBoxButtons.OK, MessageBoxIcon.Error);
}
}
private bool stillRun()
{
if (tsp != null) // Если выполнянется поиск решения
{
StatusLabel.Text = "Нельзя изменять список городов во время работы алгоритма";
StatusLabel.ForeColor = Color.Red;
return true;
}
return false;
}
// Очистка списка городов
private void clearCityListButton_Click(object sender, EventArgs e)
{
if (stillRun()) return;
cityList.Clear();
this.DrawCityList(cityList);
}
// Размещает город на карте в точке мышиного удара
private void tourDiagram_MouseDown(object sender, MouseEventArgs e)
{
if (stillRun()) return;
cityList.Add(new City(e.X, e.Y)); // e.X, e.Y - координаты мыши в физической системе координат
this.DrawCityList(cityList);
}
}
// Класс Program предоставляет метод Main для точки входа (entry point)
static class Program
{
[STAThread] // Точка входа приложения
static void Main()
{
Application.Run(new TspForm());
}
}
// Класс TspEventArgs устанавливает аргументы события, при наступлении которого отображается очередной лучший маршрут
public class TspEventArgs : EventArgs
{
// Конструктор, устанавливающий значения свойств события
public TspEventArgs(Cities cityList, Tour bestTour, int generation, bool done, int imprv)
{
this.cityList = cityList; // Список городов
this.bestTour = bestTour; // Лучший маршрут
this.generation = generation; // Номер поколения
this.done = done; // Флаг завершения алгоритма
this.imprv = imprv; // Число улучшений решения
}
// Список городов (private копия и public)
private Cities cityList;
public Cities CityList
{
get
{
return cityList;
}
}
// Лучший маршрут (private копия и public)
private Tour bestTour;
public Tour BestTour
{
get
{
return bestTour;
}
}
// Номер поколения, в котором появился текущий лучший маршрут (private копия и public)
private int generation;
public int Generation
{
get
{
return generation;
}
set
{
generation = value;
}
}
// Флаг завершения алгоритма (private копия и public)
private bool done = false;
public bool Done
{
get
{
return done;
}
set
{
done = value;
}
}
// Число улучшений маршрута (private копия и public)
private int imprv;
public int Imprv
{
get
{
return imprv;
}
set
{
imprv = value;
}
}
}
// Класс City обеспечивает формирование и хранение позиции города (свойство Location),
// хранение в списке Distances расстояний от текущего города до всех прочих городов,
// формирование (метод FindClosestCities) и хранение списка CloseCities городов-соседей текущего города
public class City
{
// Конструктор, обеспечивающий формирование позиции города
public City(int x, int y)
{
Location = new Point(x, y); // System.Drawing.Point class
}
// Позиция города (private копия и public)
private Point location;
public Point Location
{
get
{
return location;
}
set
{
location = value;
}
}
// Расстояния от города до каждого из прочих городов (private копия и public)
// Индекс списка - это номер соответствующего города
private List<double> distances = new List<double>();
public List<double> Distances
{
get
{
return distances;
}
set
{
distances = value;
}
}
// Список городов-соседей (private копия и public)
private List<int> closeCities = new List<int>();
public List<int> CloseCities
{
get
{
return closeCities;
}
}
// Находит для текущего города его города-соседи (их число равно numberOfCloseCities)
// Помещает их в список closeCities
public void FindClosestCities(int numberOfCloseCities)
{
double shortestDistance;
int shortestCity = 0;
int dCnt = Distances.Count;
double[] dist = new double[dCnt];
// Копируем список расстояний города до прочих городов в массив dist
Distances.CopyTo(dist);
closeCities.Clear();
for (int i = 0; i < numberOfCloseCities; i++)
{
shortestDistance = Double.MaxValue;
for (int city = 0; city < dCnt; city++)
{
if (dist[city] < shortestDistance)
{
shortestDistance = dist[city];
shortestCity = city;
}
}
closeCities.Add(shortestCity);
dist[shortestCity] = Double.MaxValue;
}
}
}
// Класс Cities содержит список городов
// Для каждого города указываются его координаты, расстояния до каждого прочего города и список городов-соседей
public class Cities : List<City>
{
// Находит и помещает в список city.Distances расстояния от выбранного города до всех прочих городов
// Находит для каждого города его numberOfCloseCities городов-соседей и помещает их в список closeCities
public void CalculateCityDistances(int numberOfCloseCities)
{
foreach (City city in this)
{
city.Distances.Clear();
Point pos = city.Location;
for (int i = 0; i < Count; i++)
{
Point pos2 = this[i].Location;
city.Distances.Add(Math.Sqrt(Math.Pow((double)(pos.X - pos2.X), 2D) + Math.Pow((double)(pos.Y - pos2.Y), 2D)));
}
}
foreach (City city in this)
{
// Находим для каждого города его numberOfCloseCities соседей
city.FindClosestCities(numberOfCloseCities);
}
}
// Формирует список городов по данным XML-файла
// Исключения:
// плохой формат XML-файла
// не задано имя XML-файла
// плохое имя файла (пара метр fileName)
// Фрагмент XML-файла
// <?xml version="1.0" encoding="utf-8" ?>
// <CitiesPos>
// <CityPos X="121" Y="132"/>
// <CityPos X="160" Y="370"/>
// ...
// </CitiesPos>
public void OpenCityList(string fileName)
{
DataSet cityDS = new DataSet();
try
{
this.Clear();
cityDS.ReadXml(fileName);
// Коллекция строк с координатами городов; X и Y - имена атрибутов тега City
DataRowCollection cities = cityDS.Tables[0].Rows;
foreach (DataRow city in cities)
{
this.Add(new City(Convert.ToInt32(city["X"]), Convert.ToInt32(city["Y"]))); // или city[0], city[1]
}
}
finally
{
cityDS.Dispose();
}
}
}
// Класс Population обеспечивает формирование начальной популяции
class Population : List<Tour>
{
// Лучший маршрут (private-копия и public), найденный генетическим алгоритмом
private Tour bestTour = null;
public Tour BestTour
{
set
{
bestTour = value;
}
get
{
return bestTour;
}
}
// Число улучшений решения (private-копия и public)
private int imprv = 0;
public int Imprv
{
set
{
imprv = value;
}
get
{
return imprv;
}
}
// Формирует популяцию - начальный набор случайных маршрутов
// populationSize - число создаваемых маршрутов (размер популяции)
// cityList - список городов
// rand - генератор случайных чисел. Обеспечивает различные результаты при запусках
// chanceToUseCloseCity - вероятность выбора города из списка городов-соседей
// numberOfCloseCities - число городов-соседей
public void CreateRandomPopulation(int populationSize, Cities cityList, Random rand, int chanceToUseCloseCity, int numberOfCloseCities)
{
int cCnt = cityList.Count; // Число городов
// В маршруте на один город больше
// Формируется цепочка городов, в которой первый и последний города совпадают
int tCnt = cCnt + 1;
int city, cCity, nextCity;
int tourCount;
int step; // Номер участка маршрута
bool[] cityUsage = new bool[cCnt]; // Список городов, не включенных в маршрут (свободных городов)
List<int> cities = new List<int>();
Tour tourTmp, tour;
// Можно ввести параметр "Начальный город маршрутов" или положить cityNumber = rand.Next(cCnt)
int cityNumber = 0; // Все маршруты в итоге будут начинаться с города cityNumber
for (tourCount = 0; tourCount < populationSize; tourCount++)
{
for (city = 0; city < cCnt; city++)
{
cities.Add(city);
cityUsage[city] = false; // true, если город city уже включен в маршрут
}
tourTmp = new Tour(cCnt);
cCity = rand.Next(cCnt); // Город, добавляемый в маршрут
tourTmp[0] = cCity; // Первый город маршрута
cityUsage[cCity] = true; // Город с номером cCity включен в маршрут
cities.Remove(cCity); // Удаляем город из списка свободных городов
nextCity = cCity;
for (step = 1; step < cCnt; step++)
{
// Подбираем следующий город маршрута
if (rand.Next(100) < chanceToUseCloseCity)
{
// Берем первый свободный город из списка городов-соседей
for (city = 0; city < numberOfCloseCities; city++)
{
nextCity = cityList[cCity].CloseCities[city];
if (!cityUsage[nextCity]) break;
}
}
// Если город nextCity уже в маршруте, то берем город из списка городов, не включенных в маршрут
if (cityUsage[nextCity])
{
nextCity = cities[rand.Next(cities.Count)];
}
cityUsage[nextCity] = true;
tourTmp[step] = nextCity; // Включаем город с номером nextCity в маршрут
cities.Remove(nextCity);
cCity = nextCity;
}
tour = new Tour(tCnt);
if (tourTmp[0] == cityNumber)
{
for (step = 0; step < cCnt; step++)
{
tour[step] = tourTmp[step];
}
}
else
{
// Ищем позицию города с номером cityNumber
int city0 = 0, m = -1, n = 0;
for (step = 0; step < cCnt; step++)
{
if (tourTmp[step] == cityNumber)
{
city0 = step;
break;
}
}
// Ставим в маршруте tour на первое место город с номером cityNumber
// и добавляем в tour города из tourTmp, расположенные после cityNumber
for (step = city0; step < cCnt; step++)
{
m++;
tour[m] = tourTmp[step];
}
// Добавляем в tour города из tourTmp, расположенные перед cityNumber
for (step = 0; step < city0; step++)
{
n++;
tour[m + n] = tourTmp[step];
}
}
tour[cCnt] = cityNumber; // Первый и последний города маршрута совпадают
// Вычисляем длину маршрута
tour.DetermineFitness(cityList);
// Добавляем маршрут в популяцию
Add(tour);
// Изменяем, если на то есть основание, информацию о лучшем маршруте
if ((bestTour == null) || (tour.Fitness < bestTour.Fitness))
{
BestTour = tour;
}
}
}
}
// Класс Tour представляет маршрут по всем городам
public class Tour : List<int>
{
// Конструктор, принимающий параметр capacity
// capacity - размер маршрута. Равен числу городов + 1
// Начальный пустой маршрут
public Tour(int capacity)
{
this.Clear();
for (int i = 0; i < capacity; i++)
{
this.Add(-1);
}
}
// Протяженность маршрута (private копия и public)
private double fitness;
public double Fitness
{
set
{
fitness = value;
}
get
{
return fitness;
}
}
// Определяет общую протяженность маршрута
// cities - список городов маршрута. Используется, чтобы получить расстояние между городами
public void DetermineFitness(Cities cities)
{
this.Fitness = 0;
for (int i = 0; i < this.Count - 1; i++)
{
this.Fitness += cities[this[i]].Distances[this[i + 1]];
}
}
public static Tour Crossover(Tour parent1, Tour parent2, Cities cityList, Random rand)
{
int cCnt = cityList.Count;
Tour child = new Tour(cCnt + 1); // Новый (дочерний) маршрут
int step; // Номер участка маршрута
// Первоначально дочерний маршрут совпадает с parent1
// Первый и последний города дочернего маршрута совпадают, как и у всех прочих маршрутов
for (step = 0; step < cCnt + 1; step++)
{
child[step] = parent1[step];
}
for (int i = 0; i < 2; i++) // Можно ввести параметр "Число скрещиваний" (i < nChanges взамен i < 2)
{
// Можно ввести параметр "Длина куска при скрещивании"; сейчас – это кусок с тремя городами
child = makeChange(child, parent2, rand, cCnt, 3);
}
return child;
}
// child - дочерний маршрут
// parent2 - второй родительский маршрут (при мутации равен child)
static Tour makeChange(Tour child, Tour parent2, Random rand, int cCnt, int nCts)
{
int step, step2, city, city2;
List<int> cities = new List<int>(); // Удаляемые из child города
List<int> cities2 = new List<int>(); // Добавляемые в child города
List<int> cities3 = new List<int>(); // Города для восполнения child
// nCts - протяженность заменяемого куска маршрута
// Берем из parent2 кусок маршрута с nCts городами и заменяем симметричный кусок в дочернем маршруте
// При мутации parent2 = child
step2 = rand.Next(cCnt - nCts);
while (step2 == 0) step2 = rand.Next(cCnt - nCts);
for (step = step2; step < step2 + nCts; step++)
{
city = child[step];
city2 = parent2[step];
child[step] = city2;
cities.Add(city); // Удаляемые из child города
cities2.Add(city2); // Добавляемые в child города
cities3.Add(city); // Города для восполнения child
}
// Исключаем из списков cities2 и cities3 города списка cities
int k, k2;
for (k = 0; k < nCts; k++)
{
city = cities[k];
for (k2 = 0; k2 < cities2.Count; k2++)
{
if (cities2[k2] == city)
{
cities2.Remove(city);
cities3.Remove(city);
break;
}
}
}
// Находим в дочернем маршруте оставшиеся в списке cities2 города и заменяем их на города из списка cities3
int clft = cities2.Count;
for (k = 0; k < clft; k++)
{
city = cities2[k];
for (step = 1; step < cCnt; step++)
{
if (child[step] == city)
{
city2 = cities3[rand.Next(cities3.Count)];
child[step] = city2;
cities3.Remove(city2);
break;
}
}
}
return child;
}
// Мутация
// Случаным образом меняем местами 2 города маршрута или 2 куска маршрута
// child - дочерний маршрут
// rand - генератор случайных чисел
public static Tour Mutate(Tour child, Random rand)
{
int tCnt = child.Count - 1;
// Можно добавить параметр flipCity - "Тип мутации"
// Если flipCity = true, то перестановка городов, иначе перестановка кусков маршрута
bool flipCity = true;
int nMutations = 2;
for (int i = 0; i < nMutations; i++) // Можно добавить параметр nMutations - "Число мутаций"
{
if (flipCity)
{
int step = 0, step2 = 0;
while (step == 0) step = rand.Next(tCnt);
while (step2 == 0 || step2 == step) step2 = rand.Next(tCnt);
int city = child[step];
child[step] = child[step2];
child[step2] = city;
}
else
{
// Можно ввести параметр mtnPiece - "Длина куска маршрута при мутации"
int mtnPiece = 3;
child = makeChange(child, child, rand, tCnt, mtnPiece);
}
}
return child;
}
}
// Класс Tsp координирует решение задачи коммивояжера
class Tsp
{
// Обработчик сообытия "Найден текущий лучший маршрут"
// sender - объект, создавший событие
// e - аргументы события. Параметр содержит информацию о лучших маршрутах
public delegate void NewBestTourEventHandler(Object sender, TspEventArgs e);
public event NewBestTourEventHandler foundNewBestTour;
// Генератор случайных чисел
Random rand;
// Список городов. Используется для расчета расстояний между городами
Cities cityList;
// Список всех маршрутов
Population population;
// Флаг завершения работы алгоритма (поиска новых поколений) (private копия и public)
private bool halt = false;
public bool Halt
{
get
{
return halt;
}
set
{
halt = value;
}
}
// Старт вычисленний (алгоритма)
// populationSize - число случайных маршрутов, создаваемых до начала вычислений
// maxGenerations - максимальное число скрещиваний
// wrGoupSize - число маршрутов, проверяемых в каждом поколении. 2 первых берутся в качестве родительских маршрутов, чьи дочерние маршруты заменят 2 худших маршрута в группе
// mutationChance - вероятность мутации дочернего маршрута
// seed - затравка датчика случайных чисел
// chanceToUseCloseCity - вероятность выбора города-соседа
// cityList - список городов
// numberOfCloseCities - число городов-соседей
public void FindBestTour(int populationSize, int maxGenerations, int wrGoupSize, int mutationChance, int seed, int chanceToUseCloseCity, Cities cityList, int numberOfCloseCities)
{
rand = new Random(seed);
this.cityList = cityList;
population = new Population();
population.CreateRandomPopulation(populationSize, cityList, rand, chanceToUseCloseCity, numberOfCloseCities);
displayTour(population.BestTour, 0, false, 0);
int generation;
for (generation = 0; generation < maxGenerations; generation++)
{
if (Halt)
{
break; // по требованию GUI
}
makeChildren(wrGoupSize, mutationChance, generation);
}
displayTour(population.BestTour, generation, true, population.Imprv);
}
// Случайным образом выбирает из популяции группу маршрутов
// После сортировки группы по возрастанию длины маршрута два первых рассматриваются как родительские маршруты
// Они участвуют в скрещивании
// Дочерний маршрут заменяет худший маршрут текущей рабочей групппы
// wrGoupSize - размер рабочей группы (число маршрутов в группе)
// mutationChance - вероятность мутации (в %) дочернего маршрута
// generation - текущее поколение
void makeChildren(int wrGoupSize, int mutationChance, int generation)
{
int[] wrGoup = new int[wrGoupSize]; // Рабочая группа
int i;
// Один и тот же маршрут может попасть в рабочую группу неоднократно
for (i = 0; i < wrGoupSize; i++)
{
wrGoup[i] = rand.Next(population.Count);
}
// Пузырьковая сортировка массива wrGoup по возрастанию длины маршрута
bool swapped = true;
int pass = 1, hold; // pass - номер прохода
while (swapped && pass < wrGoupSize)
{
swapped = false;
for (i = 0; i < wrGoupSize - pass; i++)
{
if (population[wrGoup[i]].Fitness > population[wrGoup[i + 1]].Fitness)
{
swapped = true; // Обмен
hold = wrGoup[i];
wrGoup[i] = wrGoup[i + 1];
wrGoup[i + 1] = hold;
}
}
pass++;
}
bool fndBestTour = false;
// Можно ввести параметр attempMax - "Число попыток улучшить популяцию"
int attemps = 0, attempMax = 1;
while (!fndBestTour && attemps < attempMax)
{
attemps++;
// 0, 1 - индексы массива wrGoup. Элементы массива wrGoup с этими индексами - это родительские маршруты
fndBestTour = makeAChild(wrGoup, mutationChance, 0, 1, wrGoupSize - 1, fndBestTour);
// Меняем родительские маршруты местами
if (!fndBestTour) fndBestTour = makeAChild(wrGoup, mutationChance, 1, 0, wrGoupSize - 2, fndBestTour);
}
if (fndBestTour) displayTour(population.BestTour, generation, false, population.Imprv);
}
// wrGoup - рабочая группа маршрутов
// p1 - индекс первого родительского маршрута в wrGoup
// p2 - индекс второго родительского маршрута в wrGoup
// bad - индекс заменяемого (плохого) маршрута в wrGoup
// fndBestTour - равен true, если в результате скрещивания и мутации получен новый лучший маршрут
bool makeAChild(int[] wrGoup, int mutationChance, int p1, int p2, int bad, bool fndBestTour)
{
int badTour = wrGoup[bad]; // badTour - индекс плохого маршрута в списке population
// Скрещиваем два лучших маршрута рабочей группы. Результат - это дочерний маршрут
// При выполнении условия rand.Next(100) < mutationChance применяем операцию мутации
// Заменяем результатом последний или предпоследний маршрут этой группы (в списке population находится в позиции badTour)
Tour child = Tour.Crossover(population[wrGoup[p1]], population[wrGoup[p2]], cityList, rand);
// Мутация дочернего маршрута
if (rand.Next(100) < mutationChance) child = Tour.Mutate(child, rand);
// Находим длину дочернего маршрута
child.DetermineFitness(cityList);
// Проверяем, имеет ли дочерний маршрут наименьшую длину
if (child.Fitness < population.BestTour.Fitness)
{
fndBestTour = true; // Найден текущий лучший маршрут
population.BestTour = child;
population.Imprv++; // Число улучшений решения
}
// Можно ввести параметр takeIfBetter – "Брать только улучшающй дочерний маршрут"
bool takeIfBetter = false;
if (takeIfBetter)
{
if (child.Fitness < population[badTour].Fitness) population[badTour] = child;
}
else
{
population[badTour] = child;
}
return fndBestTour;
}
// Порождает событите, воспринимаемое GUI, отображающим маршрут
// bestTour - лучший на текущей момент маршрут
// generationNumber - число порожденных поколений
// done - если true, то вычисления завершаются
// imprv - число улучшений решения
void displayTour(Tour bestTour, int generationNumber, bool done, int imprv)
{
this.foundNewBestTour(this, new TspEventArgs(cityList, bestTour, generationNumber, done, imprv));
}
}
}
В приведенной программе указаны возможности введения дополнительных управляющих параметров:
Возможно, это улучшит качество результата.
Можно так же ввести программное управление параметрами взамен ручного, то есть запускать приложение неоднократно, меняя автоматически значения входных данных.
Рассмотрение примера познавательно с учебных целей, поскольку он:
Ниже приведено содержимое файла CitiesPos.xml с координатами городов; маршрут, найденный для этих городов, показан на рис. 1.
<?xml version="1.0" encoding="utf-8" ?>
<CitiesPos>
<CityPos X="160" Y="370"/>
<CityPos X="121" Y="132"/>
<CityPos X="58" Y="234"/>
<CityPos X="41" Y="213"/>
<CityPos X="143" Y="86"/>
<CityPos X="312" Y="176"/>
<CityPos X="121" Y="264"/>
<CityPos X="231" Y="366"/>
<CityPos X="380" Y="62"/>
<CityPos X="202" Y="260"/>
<CityPos X="241" Y="12"/>
<CityPos X="23" Y="356"/>
<CityPos X="43" Y="317"/>
<CityPos X="175" Y="134"/>
<CityPos X="260" Y="125"/>
<CityPos X="277" Y="370"/>
<CityPos X="312" Y="153"/>
<CityPos X="23" Y="256"/>
<CityPos X="313" Y="297"/>
<CityPos X="131" Y="96"/>
<CityPos X="87" Y="67"/>
<CityPos X="249" Y="283"/>
<CityPos X="307" Y="234"/>
<CityPos X="159" Y="167"/>
<CityPos X="285" Y="123"/>
<CityPos X="12" Y="34"/>
<CityPos X="85" Y="356"/>
<CityPos X="387" Y="125"/>
<CityPos X="135" Y="268"/>
<CityPos X="185" Y="345"/>
<CityPos X="75" Y="314"/>
<CityPos X="275" Y="45"/>
<CityPos X="313" Y="78"/>
<CityPos X="110" Y="67"/>
<CityPos X="256" Y="215"/>
<CityPos X="314" Y="164"/>
<CityPos X="342" Y="186"/>
<CityPos X="331" Y="214"/>
<CityPos X="141" Y="275"/>
<CityPos X="67" Y="369"/>
</CitiesPos>
1. MichaelLaLena. www.lalena.com, 2006 г.