Создается приложение, имитирующее процесс перемещения спутника по орбите и процесс корректировки его орбиты.
Используемая модель орбиты спутника – окружность. При движении спутник может терять высоту, и тогда может возникнуть задача возвращения спутника на его расчетную орбиту. Могут быть и иные причины для корректировки орбиты спутника.
В создаваемом приложении корректировка орбиты спутника осуществляется за счет изменения высоты его полета.
Приложение создается как проект C#. Графика реализована средствами OpenGL.
Спутник перемещается в неоднородном магнитном поле Земли. Если в спутнике имеется конструктивно связанный со спутником виток с током, ориентированный по полю (рис. 1), то возникнет сила, действующая на виток и, следовательно, на спутник.
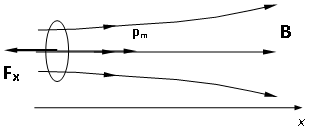
Рис. 1. Виток с током в неоднородном магнитном поле, ориентированный по полю
В формуле расчета силы
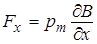
Вектор индукции магнитного поля Земли в локальной системе координат спутника может быть ориентирован, как показано на рис. 2.
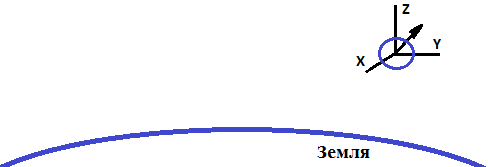
Рис. 2. Вектор индукции магнитного поля Земли
Для перемещения спутника на нужную орбиту необходимо осуществить соответствующую последовательность воздействий на спутник.
Каждое воздействие характеризуется позицией, в которой через имеющейся на спутнике виток пропускается ток, направлением и силой тока. Кроме того, виток следует ориентировать по полю. В противном случае виток будет ориентироваться по полю таким образом, чтобы векторы магнитной индукции поля и магнитного момента витка совпадали. Если виток конструктивно привязан к спутнику, то вращающий момент, действующий на виток с током в магнитном поле, будет действовать и на спутник.
В приводимой ниже программе предполагается, что
Воздействия, возвращающие спутник на заданную орбиту, не рассматриваются.
При расчете полагается, что виток ориентирован по магнитному полю Земли, известны направление и сила пропускаемого через виток тока. Так же задано и время воздействия, то есть время, в течение которого ток пропускается через виток.
Расчет выполняется по следующей схеме:
Для упрощения модели полагается, что спутник движется по круговой орбите с неизменной широтой. С учетом этого обстоятельства предварительно рассчитывается индукция в точках орбиты спутника. В каждой точке находится проекция вектора индукции на линию, соединяющую центр Земли с точкой орбиты (рис. 3).
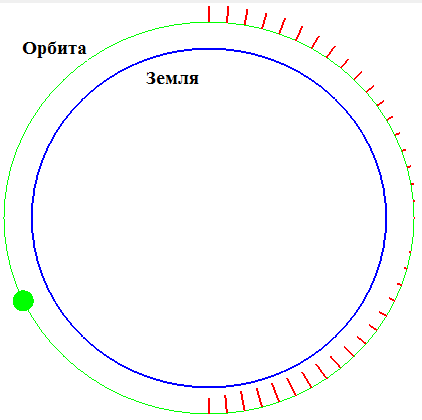
Рис. 3. Распределение радиальной проекции вектора индукции магнитного поля Земли по орбите спутника
Результаты расчета заносятся в массив, используемый далее при определении величины корректирующей силы. Одновременно формируется массив радиальных проекций индукции магнитного поля Земли в точках орбиты, радиус которой превышает радиус орбиты спутника на dH. В программе эти массивы имеют соответственно имена arrB и arrBH.
Показан на рис. 4.
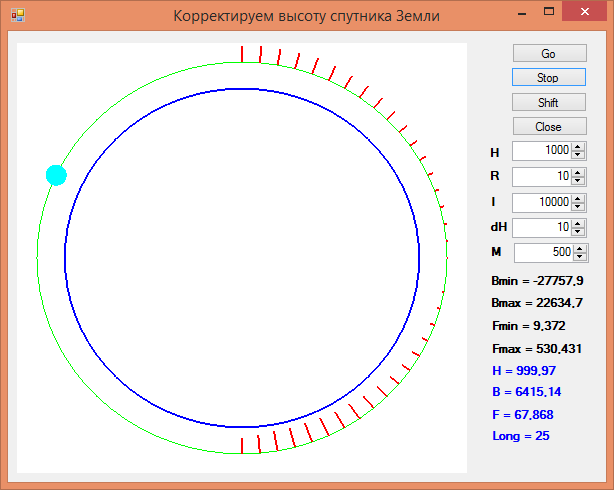
Рис. 4. Интерфейс приложения
Интерфейс позволяет:
После запуска процесса корректировки высоты в форме дополнительно отображаются:
Программа, реализующая рассматриваемую модель, имеет следующие процедуры:
Объект Timer добавляется в проект (размещается непосредственно под формой, рис. 5) в результате выполнения цепочки ToolBox - Components - Timer. Меню ToolBox, если оно отсутствует, можно показать посредством меню VIEW - ToolBox, или нажав Ctrl+Alt+X.
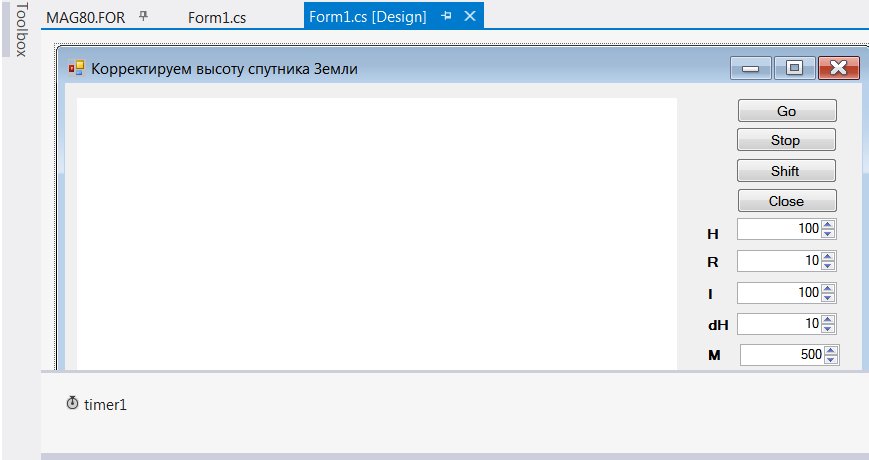
Рис. 5. Добавление объекта Timer
Ниже приводится весь код формы приложения.
using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;
// OpenGL
using Tao.OpenGl;
using Tao.Platform.Windows;
namespace gGst
{
public partial class Form1 : Form
{
public bool stp = false, sft = false; // Флаги остановки и перехода в режим корректировки высоты
public int KG = 10; // Число гармоник в модели расчета магнитного поля Земли
public double RG = 0; // Коэффициент перевода "радиан - градус"
public double GR = 0; // Коэффициент перевода "градус - радиан"
public double Lat = 57; // Широта в градусах
public double Long = 0; // Долгота в градусах
public double rZ = 6371.2; // Радиус Земли (км)
public double HZS = 0; // Плановая высота полета спутника над Землей
public double hZ = 0; // Текущая высота спутника
public double dHZ = 0.000001; // Коэффициент снижения высоты спутника за один интервал таймера
public double ba = 0; // Максимальное значение радиальной проекции индукции магнитного поля Земли
public double GS = 90, GND = -90; // Диапазон изменения долготы позиции спутника (в градусах)
public double dF = -5; // Шаг по долготе в градусах
public double kB = 0; // Коэффициент масштабирования отображаемого значения индукции
public double sptnkNgl = 0, dNgl = 1; // Угловое отклонение спутника от начальной позиции и шаг изменения этого отклонения
public double pi = 2.0 * Math.Asin(1); // Число π (в радианах)
public double pi2 = Math.Asin(1);// Число π / 2 (в радианах)
public double[] arrB = new double[1000]; // Массивы радиальных проекций индукции
public double[] arrBH = new double[1000];
public double[] arrLng = new double[1000]; // Массив значений долготы в расчетных точках орбиты
public int nB = -1; // Число расчетных точек на орбите спутника
//public System.IO.StreamWriter txtFl = new System.IO.StreamWriter(@"G:\gGst.txt");
public Form1()
{
InitializeComponent();
GM.InitializeContexts();
H.Value = H.Maximum;
IV.Value = IV.Maximum;
checkBoxFl.Checked = false;
RG = 180.0 / pi;
GR = 1.0 / RG;
labelGlng.Text = "";
labelB.Text = "";
labelF.Text = "";
labelHZ.ForeColor = System.Drawing.Color.Red;
labelGlng.ForeColor = System.Drawing.Color.Blue;
labelB.ForeColor = System.Drawing.Color.Blue;
labelF.ForeColor = System.Drawing.Color.Blue;
}
private void GM_Load(object sender, EventArgs e)
{
biba();
Gl.glEnable(Gl.GL_POINT_SMOOTH);
}
// Показывает поверхность Земли или орбиту спутника
private void showSrfc(int hw)
{
double gl = 0, gl2 = 0, dGl = 5;
double cs = 0, sn = 0, y0 = 0, z0 = 0, y2 = 0, z2 = 0, rh = 0;
Gl.glLineWidth(hw);
if (hw == 1)
{
Gl.glColor3f(0, 1, 0);
rh = rZ + hZ;
}
else
{
Gl.glColor3f(0, 0, 1);
rh = rZ;
}
Gl.glBegin(Gl.GL_LINES); // Поверхность Земли (hw = 2) или орбита спутника (hw = 1)
gl = 0;
cs = Math.Cos(gl);
sn = Math.Sin(gl);
y0 = rh * cs;
z0 = rh * sn;
while (gl < 360)
{
gl += dGl;
gl2 = gl * GR;
cs = Math.Cos(gl2);
sn = Math.Sin(gl2);
y2 = rh * cs;
z2 = rh * sn;
Gl.glVertex2d(y0, z0);
Gl.glVertex2d(y2, z2);
y0 = y2;
z0 = z2;
}
Gl.glEnd();
}
private void biba()
{
// Параметры модели
hZ = (double)H.Value; // Высота спутника над Землей (км)
HZS = hZ; // Высота, на которой должен находиться спутник
double dH = (double)dHV.Value;
double bi = 10000000;
double fi = 10000000, fa = 0, f = 0;
double b = 0, bH = 0;
Long = GS;
nB = -1;
while (Long >= GND)
{
b = MAP80(0); // Радиальная проекция индукции в текущей позиции спутника (высота hZ)
bH = MAP80(dH); // Радиальная проекция индукции в позиции (Long, Lat, hZ + dH)
nB++;
// Массивы радиальных проекций индукции
arrB[nB] = b;
arrBH[nB] = bH;
arrLng[nB] = Long;
f = frc(b, bH); // Сила, действующая на виток с током
bi = Math.Min(b, bi);
ba = Math.Max(b, ba);
fi = Math.Min(f, fi);
fa = Math.Max(f, fa);
Long += dF;
}
// Отображаем граничные значения радиальных проекций индукции и силы в форме
labelBi.Text = "Bmin = " + Math.Round(bi, 1);
labelBa.Text = "Bmax = " + Math.Round(ba, 1);
labelFi.Text = "Fmin = " + Math.Round(fi, 3);
labelFa.Text = "Fmax = " + Math.Round(fa, 3);
//txtFl.Close();
//checkBoxFl.Checked = false;
// Формируем матрицу проецирования
kB = rZ / 10 / ba;
ba = ba * kB;
double w2 = 1.01 * (rZ + hZ + ba);
Gl.glMatrixMode(Gl.GL_PROJECTION);
Gl.glLoadIdentity();
Gl.glOrtho(-w2, w2, -w2, w2, -w2, w2);
Gl.glMatrixMode(Gl.GL_MODELVIEW);
Gl.glLoadIdentity();
stp = false;
}
// Показывает радиальную проекцию индукции в графическом окне вывода
private void showB()
{
double gl = 0;
double rH = rZ + hZ;
double cs = 0, sn = 0, y0 = 0, z0 = 0, b = 0;
Gl.glColor3f(1, 0, 0);
Gl.glBegin(Gl.GL_LINES); // Векторы индукции
Long = GS;
int k = -1;
while (Long >= GND)
{
k++;
b = arrB[k]; // Радиальная проекция индукции в текущей позиции спутника (высота hZ)
Long = arrLng[k];
gl = Long * GR;
// Подготовка к отображению радиальной проекции индукции
cs = Math.Cos(gl);
sn = Math.Sin(gl);
y0 = rH * cs;
z0 = rH * sn;
b *= kB;
// Отображение радиальной проекции индукции
Gl.glVertex2d(y0, z0); // Позиция спутника
Gl.glVertex2d(y0 + b * cs, z0 + b * sn);
Long += dF;
}
Gl.glEnd();
}
// Возвращает значение силы, действующей на виток в неоднородном магнитном поле
// Виток ориентирован по полю
private double frc(double b, double bH)
{
// F = - pm * dB / dH
// pm = I * S
double sR = (float)sptnkR.Value * 3.5;
double pm = (double)IV.Value * pi * sR * sR;
double dH = (double)dHV.Value;
//b = MAP80(0);
//bH = MAP80(dH);
return Math.Abs(pm * (bH - b) / dH / 1000000.0);
}
// Вычисляет положение спутника и показывает спутник в найденной позиции
// При наличии корректирующего воздействия вычисляет значение силы,
// действующей на виток с током, а затем величину радиального перемещения спутника,
// в результате воздействия на спутник корректирующей силы
// Время действия силы равно интервалу таймера
private void showSpc()
{
double sptnkNgl2 = sptnkNgl / RG;
double xSptnk = (rZ + hZ) * Math.Cos(sptnkNgl2);
double ySptnk = (rZ + hZ) * Math.Sin(sptnkNgl2);
double glng = 0, b = 0, bH = 0;
if (sft && hZ < HZS)
{
if (sptnkNgl >= 0 && sptnkNgl < 90)
glng = sptnkNgl;
else if (sptnkNgl >= 90 && sptnkNgl < 270)
glng = 180.0 - sptnkNgl;
else
glng = sptnkNgl - 360.0;
// Берем из массивов значения b и bH радиальной проекции индукции
for (int i = 0; i < nB; i++)
{
b = arrB[i];
bH = arrBH[i];
Long = arrLng[i];
if (glng > Long) break;
}
double f = frc(b, bH); // Корректирующая сила
double a = f / (double)MV.Value; // Ускорение спутника: делим силу на массу спутника
double tFrc = 0.001 * timer1.Interval; // Время действия корректирующей силы (в секундах)
hZ += 0.5 * a * tFrc * tFrc; // Новая высота спутника над поверхностью Земли
labelHZ.ForeColor = System.Drawing.Color.Blue;
labelGlng.Text = "Long = " + Math.Round(glng, 1);
labelB.Text = "B = " + Math.Round(b, 2);
labelF.Text = "F = " + Math.Round(f, 3);
labelHZ.Text = "H = " + Math.Round(hZ, 2);
Gl.glColor3f(0, 1, 1);
}
else
{
sft = false;
labelHZ.ForeColor = System.Drawing.Color.Red;
labelGlng.Text = "";
labelB.Text = "";
labelF.Text = "";
Gl.glColor3f(0, 1, 0);
}
// Отображаем спутник в текущей позиции
float sR = (float)sptnkR.Value;
Gl.glPointSize(2 * sR);
Gl.glBegin(Gl.GL_POINTS);
Gl.glVertex2d(xSptnk, ySptnk);
Gl.glEnd();
sptnkNgl += dNgl;
if (sptnkNgl > 360) sptnkNgl = 0;
//
//double AMAG = Math.Sqrt(bX * bX + bY * bY + bZ * bZ); // (Гам) Модуль вектора поля
//double PSI = RG * Math.Asin(Z / AMAG); // (Градус) наклонение вектора поля от горизонтальной плоскости
//AMAG = 0.00001 * AMAG; // (Эрстед) Модуль вектора поля
//double TET = RG * Math.Atan(bY / bX); // (Градус) склонение вектора поля в горизонтальной плоскости
}
private void button1_Click(object sender, EventArgs e) // Go
{
biba();
}
// Вычисление вектора магнитного поля
// QK, HK - коэффициенты для полиномов Лежандра магнитного поля Земли 1980 года
private double MAP80(double dH)
{
double hZ2 = hZ + dH;
double bX = 0, bY = 0, bZ = 0; // Компоненты вектора индукции магнитного поля Земли
double[] SL = new double[12];
double[] CL = new double[12];
double[,] S = new double[12, 12], DP = new double[12, 12], P = new double[12, 12], XK = new double[12, 12];
double[] QK = new double[65] {-29988, -1957, -1997, 3028, 1662, 1279,
-2181, 1251, 833, 938, 783, 398, -419, 199, -219,
357, 261, -74, -162, -48, 49, 65, 42, -192, 4, 14,
-108, 70, -59, 2, 20, -13, 1, 11, -2, 20, 7, 1, -11,
-7, 4, 3, 7, -1, 6, 11, 2, -12, 9, -3, -1, 7, 1, -5,
-3, -4, 2, -5, -2, 5, 3, 1, 2, 3, 0};
double[] HK = new double[65] {0, 5606, 0, -2129, -199, 0, -335, 271, -252, 0, 212, -257,
53, -298, 0, 46, 149, -150, -78, 92, 0, -15, 93, 71,
-43, -2, 17, 0, -83, -28, -5, 16, 18, -23, -10, 0,
7, -18, 4, -22, 9, 16, -13, -15, 0, -21, 16, 9, -5,
-7, 9, 10, -6, 2, 0, 1, 1, 2, 5, -4, -1, -2, 4, -1, -6};
double A = 6378.16, B = 6356.776;
double A2 = A * A;
double B2 = B * B;
double A4 = A2 * A2;
double B4 = B2 * B2;
int K = KG + 1;
double FI = Lat * GR;
double XLB = Long * GR;
double ST = Math.Sin(FI);
double CT = Math.Cos(FI);
double D = ST/CT;
double Y = 0, Y1 = 0;
ST = ST * ST;
CT = CT * CT;
double R = Math.Abs(A2 * CT + B2 * ST);
double C = hZ2 * Math.Sqrt(R);
double FIC = Math.Atan((B2 + C) * D / (A2 + C));
double RX = Math.Abs(hZ2 * hZ2 + 2.0 * C + (A4 * CT + B4 * ST) / R);
R = Math.Sqrt(RX) * 1000.0;
double TE = 1.57079633 - FIC;
ST = Math.Sin(TE);
CT = Math.Cos(TE);
S[1, 1] = 1.0;
int N, M, NM1, MM1;
for (N = 2; N <= K; N++)
{
NM1 = N - 1;
Y = NM1;
S[N, 1] = S[NM1, 1] *(2.0 * Y - 1.0) / Y;
double G = Math.Abs(2.0 * Y / (Y + 1.0));
S[N, 2] = Math.Sqrt(G) * S[N, 1];
if (N > 2) {
for (M = 3; M <= N; M++)
{
MM1 = M - 1;
Y1 = MM1;
double G1 = Math.Abs((Y - Y1 + 1.0) / (Y + Y1));
S[N, M] = S[N, MM1] * Math.Sqrt(G1);
}
}
}
P[1, 1] = 1;
P[2, 1] = CT;
DP[2, 2] = CT;
DP[1, 1] = 0;
DP[2, 2] = CT;
P[2, 2] = ST;
DP[2, 1] = -ST;
for (N = 3; N <= K; N++)
{
NM1 = N - 1;
for (M = 1; M <= K; M++)
{
MM1 = M - 1;
if (M < N)
{
Y = NM1 - 1.0;
Y1 = MM1;
XK[N, M] = (Y * Y - Y1 * Y1) / ((2.0 * Y + 1.0) * (2.0 * Y - 1.0));
P[N, M] = CT * P[NM1, M] - XK[N, M] * P[N-2, M];
DP[N, M] = CT * DP[NM1, M] - ST * P[NM1, M] - XK[N, M] * DP[N - 2, M];
}
else if (M > N)
{
P[N, M] = 0;
DP[N, M] = 0;
}
else
{
P[N, M] = ST * P[NM1, MM1];
DP[N, M] = ST * DP[NM1, MM1] + CT * P[NM1, MM1];
}
}
}
for (N = 1; N <= K; N++)
for (M = 1; M <= N; M++)
{
P[N, M] = P[N, M] * S[N, M];
DP[N, M] = DP[N, M] * S[N, M];
}
R = rZ * 1000.0 / R;
for (M = 1; M <= K; M++)
{
Y1 = M - 1.0;
SL[M] = Math.Sin(Y1 * XLB);
CL[M] = Math.Cos(Y1 * XLB);
}
if (Math.Abs(ST) < 0.0000001)
A = 0.00000001;
else
A = ST;
int J = -1;
for (N = 2; N <= K; N++)
for (M = 1; M <= N; M++)
{
J++;
B = Math.Pow(R, N + 1);
C = (QK[J] * CL[M] + HK[J] * SL[M]) * B;
bX = bX + C * DP[N, M];
bY = bY + (QK[J] * SL[M] - HK[J] * CL[M]) * (M - 1.0) / A * P[N, M] * B;
bZ = bZ - N * C * P[N, M];
}
D = FI - FIC;
ST = Math.Sin(D);
CT = Math.Cos(D);
bX = bX * CT + bZ * ST;
bZ = bZ * CT - bX * ST;
double nglX = 0, nglZ = 0;
double b = Math.Sqrt(bX * bX + bY * bY + bZ * bZ);
nglX = Math.Abs(Math.Atan(bX / bY));
nglZ = Math.Abs(Math.Atan(bZ / bY));
b = b * Math.Cos(FI + nglX - pi2);
b = b * Math.Cos(XLB - nglZ);
//string st = "";
//st = "" + Math.Round(Lat, 1) + "\t" + Math.Round(Long, 1) + "\t" + Math.Round(X, 1) + "\t" + Math.Round(Y, 1) + "\t" + Math.Round(Z, 1) + "\t" + Math.Round(nglX * RG, 1) + "\t" + Math.Round(nglZ * RG, 1) + "\t" + Math.Round(b, 1);
//if (checkBoxFl.Checked) txtFl.WriteLine(st);
// Возвращает значение радиальной проекции индукции в заданной позиции
return b;
}
private void button2_Click(object sender, EventArgs e) // Close
{
Close();
}
private void button3_Click(object sender, EventArgs e) // Stop
{
stp = true;
}
private void numericUpDown1_ValueChanged(object sender, EventArgs e) // hZ
{
hZ = (double)H.Value; // Высота спутника над Землей (км)
HZS = hZ;
stp = true; // Останавливаем модель
}
private void buttonShift_Click(object sender, EventArgs e) // Shift
{
stp = false; // Запускаем модель
sft = true; // Переходим в режим корректировки высоты
}
private void timer_Tick(object sender, EventArgs e)
{
if (!stp)
{
Gl.glClearColor(1, 1, 1, 1); // Цвет фона
Gl.glClear(Gl.GL_COLOR_BUFFER_BIT);
showSrfc(1); // Показываем контур Земли
showSrfc(2); // Показываем орбиту спутника
showB(); // Показываем радиальные проекции вектора магнитной индукции Земли
showSpc(); // Вычисляем позицию спутника и показываем спутник в этой позиции
Gl.glFlush();
GM.Invalidate();
hZ -= hZ * dHZ; // Высота спутника над Землей (км)
labelHZ.Text = "H = " + Math.Round(hZ, 2);
}
}
}
}
Демонстрационные фильм, показывающий изменение орбиты спутника, создается в 3ds Max следующим MaxScript-кодом:
-- Скрывает или показывает виток с током на спутнике за счет управления свойством render_thickness
-- Изменяет размеры орбиты спутника (llps.length и llps.width)
function nmtCr tP L W dt cr k k2 = (
at time (tP - 1) (
cr.render_thickness = 0
llps.length = L * k
llps.width = W * k
)
at time tP cr.render_thickness = 5
at time (tP + dt) (
cr.render_thickness = 5
llps.length = L * k2
llps.width = W * k2
)
at time (tP + dt + 1) cr.render_thickness = 0
)
-- Создает виток с током на спутнике
function mkCr cr rS clr sptnk = (
cr = copy cr
cr.radius = rS
cr.wireColor = clr
cr.parent = sptnk
cr.pos = sptnk.pos
cr.render_thickness = 0
cr
)
-- Показывает магнитный полюс Земли
function shPl rZ Lat Long sp vrnt = (
cH = 12
sng = if vrnt == "S" then 1 else -1
cs = cos Lat
xPl = sng * rZ * cs * (cos Long)
yPl = -sng * rZ * cs * (sin Long)
zPl = sng * rZ * (sin Lat)
clr = if vrnt == "S" then (color 255 0 0) else (color 0 0 255)
pl = cone radius1:2 radius2:0 pos:[xPl, yPl, zPl] height:cH wireColor:clr
pl.rotation.X_Rotation = if vrnt == "S" then 0 else 180
pl.rotation.Y_Rotation = if vrnt == "S" then -sng * acos (zPl / rZ) else 0
pl.rotation.Z_Rotation = atan (xPl / yPl)
pl.parent = sp
pl2 = copy pl
pl2.wireColor = (color 0 0 255)
pl2.rotation.X_Rotation = 180
pl2.pos = [-xPl, -yPl, -zPl]
pl2.parent = sp
)
delete $*
nSgs = 32
btMp = Bitmaptexture fileName:"C:\Shoya\GeoGost\earth.jpg"
mt = standard diffuseMap:btMp showInViewport:on
--meditMaterials[1] = mt
rZ = 63.712
rZ = 0.5 * rZ
-- Земля
sp = sphere radius:rZ segs:nSgs wireColor:white
sp.material = mt
rotate sp (angleaxis 11.2501 [0,0,1])
--South magnetic pole (2004): 63.3° south latitude and 138.0° east longitude
-- Показываем южный магнитный полюс Земли
shPl rZ 63.3 138.0 sp "S"
-- North magnetic pole (2004): 82.18° south latitude and 113.24° east longitude
-- Показываем северный магнитный полюс Земли
--shPl rZ 82.18 113.24 sp "N"
-- cr и cr2 - соответственно нулевые меридианы и параллель (экватор)
cr = circle radius:rZ render_renderable:on render_displayRenderMesh:on render_thickness:1 wireColor:yellow
cr2 = copy cr
cr2.wireColor = yellow
rS = 8
rotate cr2 (angleaxis 90 [0, 1, 0])
cr.parent = sp
cr2.parent = sp
L = 4 * rZ
W = 5 * rZ
-- llps и llps2 - это орбиты спутника соответственно текущая и скорректированная
llps = Ellipse length:L width:W pos:[0,0,0] steps:24 render_renderable:on render_displayRenderMesh:on render_thickness:1 wireColor:white
rotate llps (angleaxis 100 [0, 1, 0])
llps2 = copy llps
llps2.wireColor = white
-- Спутник
sptnk = sphere radius:rS segs:nSgs wireColor:green
-- Витки с током на спутнике: красный - смещение спутника вверх, синий - вниз
cr3 = mkCr cr rS (color 255 0 0) sptnk
cr4 = mkCr cr rS (color 0 0 255) sptnk
pc = Path_Constraint ()
pc.path = llps
pc.Percent.Keys[2].Value = 200
sptnk.pos.controller = pc
rng = 500f
tP = 0.22 * rng
dt = 20
tP2 = 3.5 * tP
animate on (
-- Вращение Земли
at time rng rotate sp (angleaxis (360.0 / 8.0) [0, 0, 1])
-- Анимация видимости витков с током на спутнике (красного и синего)
nmtCr tP L W dt cr3 1 1.1
nmtCr tP2 L W dt cr4 1.1 1
)
sp.rotation.Z_Rotation.controller.keys[1].outTangentType = #linear
sp.rotation.Z_Rotation.controller.keys[2].inTangentType = #linear
animationRange = interval 1 rng
playAnimation()
Файл earth.jpg, используемый для создания текстуры, показан на рис. 6.
Рис. 6. Карта Земли
Анимацию можно посмотреть ниже.
Одно направление тока в витке, расположенном на спутнике, вызывает подъем спутника, противоположное - его снижение.
Второе видео показывает взаимодействие спутников, осуществляемое с целью обмена информацией, доставляемой в конечном счете потребителю.
Видео создается следующим кодом:
-- Анимация конусов видимости
function nmtCn t dt h h2 r r2 arrCn = (
for k = 1 to 6 do at time t (
arrCn[k].height = h
arrCn[k].radius2 = r2
)
for k2 = 1 to 2 do (
t += dt
for k = 1 to 6 do at time t (
arrCn[k].height = h2
arrCn[k].radius2 = r
)
)
t += 1
for k = 1 to 6 do at time t (
arrCn[k].height = h
arrCn[k].radius2 = r2
)
t
)
-- Анимация межспутниковых лучей
function nmtClBm t dt arrCl h rCr = (
for k = 1 to 6 do (
at time t arrCl[k].height = h
t += dt; at time t arrCl[k].height = -rCr
t += 1; at time t arrCl[k].height = h
)
t
)
-- Добавляет в массив цилиндрический зондирующий луч
function ppndCl x y z h clRt clr arrCl = (
cl = cylinder radius:2 height:h pos:[x, y, z] wireColor:clr
cl.rotation.Y_rotation = clRt
append arrCl cl
)
-- Добавляет в массив конус видимости
function ppndCn x y z h clRt clr r arrCn = (
cn = cone radius1:0 radius2:r height:h pos:[x, y, z] wireColor:yellow
cn.rotation.Y_rotation = clRt
append arrCn cn
)
-- Анимация зондирующих лучей
function nmtCl t arrCl h = (
at time t for k = 1 to 6 do arrCl[k].height = h
)
delete $*
nSgs = 32
btMp = Bitmaptexture fileName:"C:\Shoya\GeoGost\earth.jpg"
mt = standard diffuseMap:btMp showInViewport:on
rZ = 63.712
rZ = 0.5 * rZ
-- Земля
sp = sphere radius:(1.3 * rZ) segs:nSgs
sp.material = mt
rotate sp (angleaxis 11.2501 [0,0,1])
-- Орбита спутников
rCr = 4 * rZ
cr = circle radius:rCr render_renderable:on render_displayRenderMesh:on render_thickness:3 wireColor:yellow steps:32
rotate cr (angleaxis 90 [1, 0, 0])
-- Отражающие слои
rCr2 = 0.7 * rCr
rCr3 = 0.5 * rCr
cr2 = circle radius:rCr2 render_renderable:on render_displayRenderMesh:on render_thickness:1 wireColor:white steps:32
rotate cr2 (angleaxis 90 [1, 0, 0])
cr3 = circle radius:rCr3 render_renderable:on render_displayRenderMesh:on render_thickness:1 wireColor:blue steps:32
rotate cr3 (angleaxis 90 [1, 0, 0])
rZ4 = 12
-- Массив спутников
arrSp = #()
-- Массивы цилиндрических зондирующих лучей
arrClW = #()
arrClB = #()
arrClR = #()
-- Массив цилиндрических сигналов для обмена данными
arrClBm = #()
-- Конусы видимости
arrCn = #()
y = 0
fi = 60
clRt = 30
clBmRt = -clRt
h = 1
clr = (color 255 255 255)
rCn = 1
-- Показываем 6 спутников
for k = 1 to 6 do (
x = rCr * (cos fi)
z = rCr * (sin fi)
sptnk = sphere radius:rZ4 wireColor:green pos:[x, y, z]
sptnk.pivot = [0, 0, 0]
-- Формируем рабочие массивы
append arrSp sptnk
ppndCl x y z h clRt clr arrClW
ppndCl x y z h clRt (color 0 0 255) arrClB
ppndCl x y z h clRt (color 255 0 0) arrClR
ppndCl x y z h clBmRt clr arrClBm
ppndCn x y z h clRt clr rCn arrCn
clRt += 60
clBmRt += 60
fi -= 60
)
arrGr = #()
for k = 1 to 6 do (
-- Создаем группу, содержающую все рабочие массивы
append arrGr arrSp[k]
append arrGr arrClW[k]
append arrGr arrClB[k]
append arrGr arrClR[k]
append arrGr arrClBm[k]
append arrGr arrCn[k]
)
dt = 3
dt2 = 150
t = dt2
rng = 6 * (dt2 + 23 * dt + 13)
animationRange = interval 1 rng
gr = group arrGr
-- Анимация отдельных объектов и группы gr
animate on (
for k4 = 1 to 6 do (
nmtCl t arrClW h
t += dt; nmtCl t arrClW (rCr2 - rCr)
t += dt; nmtCl t arrClW (rCr2 - rCr)
t += dt; nmtCl t arrClW h
nmtCl t arrClB h
t += dt; nmtCl t arrClB (rCr3 - rCr)
t += dt; nmtCl t arrClB (rCr3 - rCr)
t += dt; nmtCl t arrClB h
nmtCl t arrClR h
t += dt; nmtCl t arrClR (rZ - rCr)
t += dt; nmtCl t arrClR (rZ - rCr)
t += dt; nmtCl t arrClR h
t = nmtClBm t dt arrClBm h rCr
t = nmtClBm t dt arrClBm h rCr
t = nmtCn t dt h (1.1 * (rZ - rCr)) 20 rCn arrCn
t += dt2
)
at time rng (
rotate sp (angleaxis (360.0 / 16) [0, 0, 1])
rotate gr (angleaxis 360.0 [0, 1, 0])
)
)
sp.rotation.Z_Rotation.controller.keys[1].outTangentType = #linear
sp.rotation.Z_Rotation.controller.keys[2].inTangentType = #linear
gr.rotation.Y_Rotation.controller.keys[1].outTangentType = #linear
gr.rotation.Y_Rotation.controller.keys[2].inTangentType = #linear
playAnimation()
Файл earth.jpg, используемый для создания текстуры, показан на рис. 6.
Хотя и приведенная модель является весьма грубой, она позволяет понять, насколько эффективен процесс корректировки орбиты спутника в результате действия силы на виток с током, ориентированный по полю и встроенный в спутник.
Для уточнения модели следует ввести в нее корректирующие воздействия, возвращающие спутник на исходную орбиту. Кроме того, наряду с другими уточнениями, нужно управлять длительностью разового воздействия и более точно определять позицию спутника, в которой он окажется в результате действия приложенных к нему сил.